高地应力下巷道底板拱结构分析及其应用
陈 盼,谷拴成
(1.西安科技大学 建筑与土木工程学院,陕西 西安 710054;2.中煤科工集团西安研究院有限公司 水文地质研究所,陕西 西安 710052)
0 引 言
深部巷道掘进后,其底板岩体在高地应力作用下将发生不同程度的变形与破坏,强烈的巷道底鼓不仅显著增加维护费用,而且严重影响煤矿的安全高效生产,已成为深部岩体工程领域研究的热点和难点[1],近年来诸多学者进行了大量的研究工作。康红普认为底板岩层的压曲、扩容和膨胀是引起矿山巷道底鼓的重要原因[2];文志杰等建立了剪切错动型巷道底臌力学模型,提出一种与剪切错动型巷道底臌力学机理相适应的新型反底拱底臌控制技术[3];孙闯建立压杆模型并提出一种估算巷道底鼓水平应力的方法[4];孟祥瑞等基于弹性模型分析底板任一点的应力状态,建立底板破坏判据[5];黄庆享等针对回采巷道底板破坏深度确定难题,建立底板破坏力学模型,分析巷道底板的极限承载力和挤压流动型变形的破坏机理[6];杨仁树等提出以“协调围岩非均匀变形、控制挤压流动底鼓、强化围岩承载结构”为核心的联合支护方案[7]。黄琪嵩等分析岩性对底板应力状态及其破坏特征的影响[8];丁国峰等分析回采巷道顶板和两帮强度对底板岩层稳定性的影响,认为加固顶板和两帮有利于控制巷道底板变形[9];孙晓明等利用压杆稳定理论建立巷道底板的挠曲破坏机理[10]。
在巷道底板稳定性控制方面,王卫军等根据底鼓机理提出通过加固两帮和底角来控制巷道底鼓的方法[11];何满潮等基于深部软岩巷道的非线性大变形破坏现象,讨论巷道底鼓的锚网索耦合支护技术[12];谢广祥等研究采用注浆锚杆配合混凝土回填控制深部巷道底鼓技术[13];张农等认为巷道底板应构建整体封闭式进行主动支护,并辅以结构补强[14];刘泉声等提出采用混凝土反底拱结合注浆、预应力锚索联合加固软岩巷道底板的方法[15];侯朝炯等分析深部巷道底鼓“两点三区”的变形特征,可以通过控制巷道顶帮来抑制底板的变形[16]。
在实际工程中,由于底板所处地质条件和力学环境的多样性和复杂性,其变形机理及控制措施也不尽相同,从而导致底板支护参数确定依然具有很大的盲目性,造成支护效果不佳。以陕西彬长矿区某煤矿回风大巷为工程背景,在总结分析前人研究成果的基础上,通过构建高地应力条件下巷道底板的隐形拱结构力学模型,分析底板拱结构的演化规律,提出底板最大破坏深度及其加固拱厚度的确定方法,为合理设计高地应力下巷道底板的锚固参数提供科学的理论依据。
1 巷道底板变形破坏力学机理
高地应力条件下,巷道开挖以后,围岩应力重新分布,在两帮形成支承压力,巷道底板除受下部岩层向上的挤压荷载,以及水平地应力作用外,还受帮部破裂区和极限平衡区支承压力作用,在这些荷载共同作用下底板岩层将由上向下逐层发生剪切滑移破坏,上部岩体逐渐从水平挤压状态向上隆起变为局部拉应力状态,实践证明,巷道围岩破坏到一定程度后即停止变形,能够形成“隐形拱状自稳结构”,使围岩保持极限平衡状态,并能长期稳定[17-18],如图1所示。
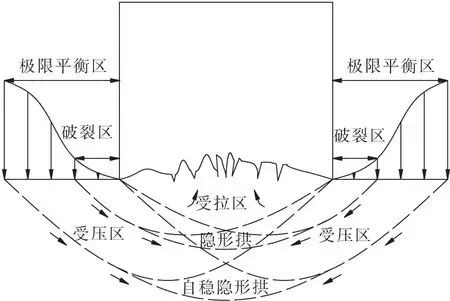
图1 巷道底鼓示意Fig.1 Sketch of floor heave
巷道底板变形破坏形成的隐形拱把底板岩体分为受拉区和受压区2部分,以拱轴线为界,在受拉区内,底板单元体中拉应力大于零,为潜在危害岩体;拉应力为零的应力单元连线形成隐形拱轴线,拱轴线处岩体只受沿拱轴线方向的压应力;拱轴线以外岩体仍然处于三向应力状态,为稳定区。文献[19]的实测结果也验证了这一点。
由于扩容作用,巷道底板受拉区的岩体体积增大,向上位移后形成底鼓。对于高地应力条件下的巷道,如果底板处于敞开不支护状态,很难在浅部形成稳定的拱结构,导致巷道底板破坏不断向深部发展,造成巷道严重底鼓。由此可见,巷道底鼓量大小主要取决于底板拱结构的位置。
2 不同侧压条件下巷道底板最大破坏深度
以巷道底板变形破坏过程中形成的自稳隐形拱为研究对象,由拱轴线的受力特征可知,拱轴线上所有点的弯矩及剪力均为零,只有轴向力的作用。根据对称性取半拱结构建立力学模型如图2所示[20]。

图2 底板拱结构计算分析模型Fig.2 Calculation and analysis model of floor arch structure
图2中,N1和N2分别为半拱结构所受轴力,qh和qv分别为半拱结构所受水平荷载和竖直荷载。取拱轴线AM进行分析,由该段拱轴线的静力平衡条件可得
(1)
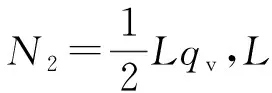
将式(1)化简得
(2)
由式(2)可见,底板自稳隐形拱结构为中心在巷道底板中点的半椭圆。
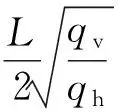
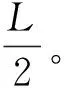
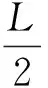
3 基于隐形拱的巷道底板支护措施
3.1 高应力下底板支护机理
由以上分析可知,巷道剧烈底鼓的原因是底板不能在浅部形成稳定的拱结构,导致拱结构一再向深部发育。故巷道底板控制的出发点是阻止巷道底板拱结构向深部发育,或在浅部构建一个拱结构以抵抗巷道底板荷载,保证底板稳定。
和巷道顶帮支护类似,底板支护应首先最大限度利用围岩的自承能力和自稳结构,故对于新掘进巷道,底板控制施工应紧跟掘进工作面,及时施加支护结构,改善底板岩层受力特征,减小围岩强度损失,防止底板自稳隐形拱结构向深部发育。若此时底板巷道围岩强度不能满足要求,需通过注浆等人工补强方式形成稳定结构。对于已经发生严重底鼓的巷道,在清理底板至设计巷道断面后,就需要采用更加有效的手段来增加底板已破坏岩体的峰后残余强度,并配合高预应力锚杆(索)等措施使其形成稳定结构。
阻止巷道底板拱结构向深部发育的主要方法是增加巷道底板岩体强度,改善巷道底板岩体受力特征。具体可采用注浆加固的方式增加底板巷道围岩强度,采用预应力锚杆(索)方式改善底板巷道围岩受力特征。如图3所示,可通过高预应力锚杆(索)配合底板注浆的方式在巷道底板构建一个挤密加固拱结构来抵抗底板荷载,以达到预防底鼓的目的。

图3 巷道底板拱结构支护机理示意Fig.3 Supporting mechanism of laneway floor arch structure
3.2 挤密加固拱有效跨度的确定
为保证所构建底板拱结构稳定,将拱脚作用在巷道帮部稳定岩体上,故挤密加固拱的跨度取巷道跨度加两帮极限破坏厚度。有效跨度L可表示为
L=l+2x0
(3)
式中L为底板拟构建挤密加固拱的跨度,m;l为巷道宽度,m;x0为巷道帮部极限平衡区宽度,m。
由文献[21]可知,巷道帮部极限平衡区宽度为
(4)
式中h为巷道高度,m;λ为侧压力系数;k为应力集中系数;H为巷道埋深,m;Px为煤帮支护阻力,MPa。
此外,为防止帮部破裂区宽度增大后影响拱脚稳定,应加强巷道帮部支护,保证帮部破裂区不再向深部发育,破裂区宽度为[22]
(5)
式中φu和φd分别为巷道顶底板与煤帮上下界面的摩擦角,(°),其他符号意义同前。
3.3 底板挤密加固拱厚度的确定
所构建底板挤密加固拱拱轴线取巷道自稳隐形拱轴线,拱轴线各截面只受沿拱轴线方向的压应力,故可以根据底板岩石抗压强度来确定挤密加固拱的厚度,拱轴线上任一点受力如图4所示。
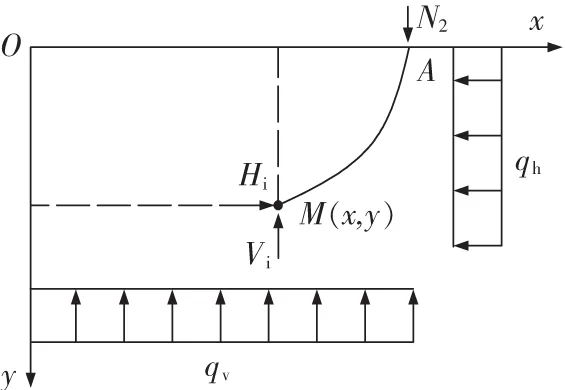
图4 挤密加固拱受力模型Fig.4 Stress model of arch strengthened by compaction
由于轴线上任意一点M(x,y)处的水平分力Hi和竖向分力Vi分别为
(6)
故拱轴线上任意一点的轴力为
(7)
假设在挤密加固拱处一定厚度范围内只受轴向压力,则该拱的受力模型就可以简化为单向轴压破坏。根据摩尔-库仑强度理论可知
(8)
式中σc,c,φ分别为底板岩体注浆改善后的单轴抗压强度、黏聚力和内摩擦角。
由式(7)和式(8)可得巷道底板挤密加固拱要保持稳定的极限最小拱圈厚度为
(9)
将式(6)代入式(9)得
(10)
由式(10)可以看出,当底板岩性参数和所受荷载一定时,极限拱圈厚度是变量(x,y)的函数,即极限拱圈厚度在拱轴线各处均不同,并呈现一定规律分布。在实际施工中,要构建厚度不等且呈一定规律变化的底板拱结构难度较大,故取最大极限拱圈厚度作为底板挤密加固拱厚度。
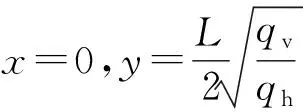
(11)

(12)
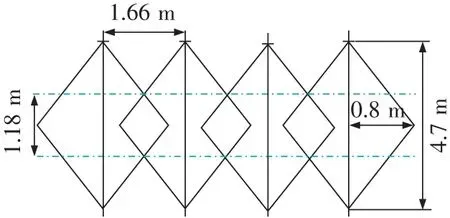
比较式(11)和式(12)可知,当qh 当qh>qv,同理可求得挤密加固拱在长轴和短轴处极限拱圈厚度分别为 (13) (14) 比较式(13)和式(14)可知,当qh>qv,挤密加固拱极限拱圈厚度同样在短轴处较大。 由以上分析可知,挤密加固拱极限拱圈厚度最大值始终位于短轴顶点处,故取式(12)和式(14)确定底板挤密加固拱厚度。 陕西彬长矿区某矿二采区回风大巷平均埋深620 m,断面尺寸为4 m×3.2 m(宽×高)。巷道开挖后,由于水平构造应力较大,且底板除采用混凝土铺底外,没有采取其他支护措施,巷道围岩出现了较大变形,底鼓现象尤为严重,如图5所示。 图5 彬长某矿二采区回风大巷底鼓现状Fig.5 Present status of floor heave in air return laneway in the second mining area of Binchang mine 现场清理底板至设计断面后,拟在底板构建拱结构治理巷道底鼓,并采用上述理论确定底板锚杆(索)的支护参数。对巷道清理底板过程中产生岩石进行现场取样,并通过实验室实测,得到底板岩体物理力学参数见表1。 表1 底板岩体计算参数取值 将表1参数代入式(4)可得巷道帮部极限平衡区宽度为 x0= (15) 将表1参数代入式(5)得煤帮破碎区宽度为 Ls= (16) 由式(3)可知,底板挤密加固拱有效跨度为 L=4+2×4.2=12.4 m (17) 由第2节可知,底板极限隐形拱为竖直方向的半椭圆,其长半轴为 (18) 同理可得短半轴为 (19) 设计底板拱结构厚度取挤密加固拱极限拱圈最大厚度,由3.3节可知,在短轴顶点处极限拱圈厚度最大,由式(12)可得 (20) 设单根锚索施加的预应力值P=180 kN,加固岩体变形模量E=8.4 GPa。由文献[23]可知,单根锚索最大加固半径为 (21) 为简化计算,把锚索作用范围在垂直平面上的剖面视为菱形。叠加挤压区按最大拱圈厚度计,根据几何关系可得锚索间距S为 (22) 式中La为所用锚索锚固段中点到孔口距离,m,全长锚固锚索取锚固段全长,选取锚索长度为5 m,La取4.7 m,将式(20)和式(21)代入(22)可得锚索间距为 (23) 根据以上计算可知,使用预应力为180 kN,长度为5 m的全长锚固锚索,当锚索间距小于1.66 m时即可形成厚度大于1.18 m的挤密加固区,如图6所示。 图6 底板加固拱计算模型Fig.6 Calculation model of arch strengthened by laneway floor 根据现场情况,基于“治底先治帮”的思路,为防止帮部2.2m破碎区向深部发育,首先在巷道煤帮部施工长度为2.5 m的预应力锚杆。底板采用“底板注浆+锚索+钢筋网片+W钢带”联合支护。考虑到底板已经发生过大变形,故首先在底板浅层施工短钻孔,预注浆,封闭底板表层裂隙,然后施工锚索孔。 根据锚索间距小于1.66 m的要求,并结合现场实际情况,设计底板锚索4根,其中巷道中间布置竖直向下锚索2根,间距1.4 m,两帮靠底角位置分别布置向外倾斜30°的锚索各一根,间距均为1.3 m,如图7所示。锚索孔施工完毕,安装锚索钢绞线后,利用锚索孔对底板进行高压注浆,最后再配合钢筋网片和W钢带完成锚索安装,带浆液凝固后,进行锚索张拉,保证每根锚索预应力大于180 kN。 图7 二采区回风大巷底板支护优化示意Fig.7 Floor support optimization of air return laneway in the second mining area 新支护方案实施后,依据矿压监测要求,在巷道布置了2个间隔15 m的围岩变形监测断面,采用十字布点法分别在巷道顶底板和两帮布置表面围岩监测点。根据近3个月的矿压监测数据分析,2个断面监测所得数据接近,两帮移近量平均为92 mm,顶板下沉量和底鼓量均较小,顶板下沉量平均仅为23 mm,底鼓量平均仅为51 m m,且围岩变形主要发生在施工完成后的35 d内,35 d以后巷道围岩已基本稳定。可以看出,采用该方法有效控制了巷道底鼓。 1)高应力条件下巷道底板变形破坏实质为底板隐形拱结构逐步向深部发育的过程,底板隐形拱的形态与底板岩层所受水平侧压力和两帮支承压力相关。 2)通过锚索(杆)支护、注浆等方法,在巷道底板中形成一定厚度的挤密加固拱,可显著改善底板岩体受力特征,阻止底板拱结构向深部发育,达到改善巷道底板稳定性的目的。 3)将上述理论应用于彬长矿区某矿回风大巷底板加固,现场测试治理段巷道平均底鼓量仅为51 mm,35 d以后巷道围岩已基本稳定,表明巷道底板变形得到了有效控制,底鼓治理效果显著。4 工程验证


4.1 巷道帮部极限平衡区宽度的确定
4.2 底板挤密加固拱半轴的确定

4.3 挤密加固拱参数的确定


5 结 论

