基于犹豫模糊语言集的大跨径斜拉桥上部结构施工安全风险评估
周 直,熊家豪,刘光凤
(重庆交通大学 经济与管理学院,重庆 400074)
近年来,媒体关于桥梁施工风险事故的报道屡见不鲜。桥梁施工一旦发生安全事故,将对经济生产、人身安全造成巨大的损失,导致非常负面的社会影响。而大跨径斜拉桥由于长跨径和特殊工艺,其上部结构的施工非常容易发生事故。因此,应该评估大跨径斜拉桥的施工风险,据此采取针对性的预控措施降低风险损失已迫在眉睫。
至今,各国学者对桥梁的风险评估做了大量的研究工作。例如,康俊涛等[1]提出一种基于贝叶斯网络理论的桥梁施工安全评价方法。朱治宝等[2]运用LEC法量化危险源,在此基础上建立基于WBS-RBS与模糊层次综合法的桥梁施工安全风险评估模型。王丹等[3]建立基于ANP的深水桥梁基础工程施工风险评估模型。刘沐宇等[4]建立基于证据理论的悬索桥主塔施工风险评估模型。刘朝阳等[5]构建基于事故树模型和改进THERP+HCR模型的桥梁工程安全预警机制。李彦等[6]建立基于决策树分析技术的桥梁施工安全风险评估模型。陈海南等[7]运用FISM方法构建跨既有铁路线桥梁转体施工安全的关键影响因素多层递阶结构,剖析事故致因机理,提出安全防护措施。张锦等[8]建立基于模糊综合评价法的川藏铁路重点桥梁和隧道风险评价模型,在此基础上,提出一种BP神经网络风险预测模型。施洲等[9]采用WBS-RBS对沉井基础施工进行风险识别,在此基础上建立基于FAHP的风险评估模型。同年,施洲等[10]提出一种基于DEMATEL和贝叶斯网络的桥梁施工动态风险评估模型。综上可知,虽然关于桥梁风险评估的研究已取得了一系列成果,但是针对斜拉桥上半部施工风险的研究还较少。此外,已有评估方法大多依赖于专家评语,而专家在给出风险评语时往往出现犹豫不决的情况,容易影响评估结果的可信度。
因此,本文首先构建施工风险的评估指标体系,然后考虑到犹豫模糊语言集在处理犹豫不决情况的突出优势,基于犹豫模糊型语言集合和层次分析法,建立评价和估计风险的模型,以期确定施工的关键风险因素和风险等级,保证结果的精确。
1 构建施工安全风险评估指标体系
影响大跨径斜拉桥上部结构施工安全的风险因素众多。本文根据施工过程的特点,将风险因素的一级指标按照施工阶段划分为桥面施工、支架施工、钢箱梁施工和斜拉索施工四个方面。在此基础上,结合类似工程数据、相关文献[11-12]、行业规范[13]、现场调研,并咨询有关专家,最终确定了16个影响斜拉桥上部结构施工安全的风险因素作为二级指标,建立风险评估的指标体系,如表1所示。

表1 评估指标体系
2 构建施工安全风险评估模型
2.1 基于HFLTS-AHP的权重计算模型
在所构建的大跨径斜拉桥上部结构施工安全风险评估指标体系基础上,运用犹豫模糊型语言集合量化专家评估的风险信息;结合层次分析的方法,得出指标各自的权重。该方法计算简单、易于操作,可以有效解决多准则群决策过程中的主观性和补偿性问题[14]。
设评估指标集合为{C1,C2,…,Cn-1,Cn},决策小组{D1,D2,…,Dk-1,Dk},其中n为指标的数目,k为专家数。可通过以下步骤求解指标权重。
2.1.1 构建犹豫模糊语言判断矩阵
设Hs为S的犹豫模糊型语言的评价术语的集合,其中S={S1,S2,…,S∂}为专业语言的集合。在本文中定义重要性语言术语集S={不重要,极低,低,中等,高,极高,绝对高},对应值如表2所示[15]。在该语言集S的基础上,专家可以使用、“少于”“多于”“至少”“至多”和“之间”等表达式来给出判断,如少于VH、至少L、至多H、M与H之间等。

表2 语言术语集的赋值
EGH是将语言运用语言GH生成的专家打分结果ll∈Sll转化为犹豫模糊语言集Hs的函数,其转换规则如下。
EGH(sj)={sj|sj∈S}
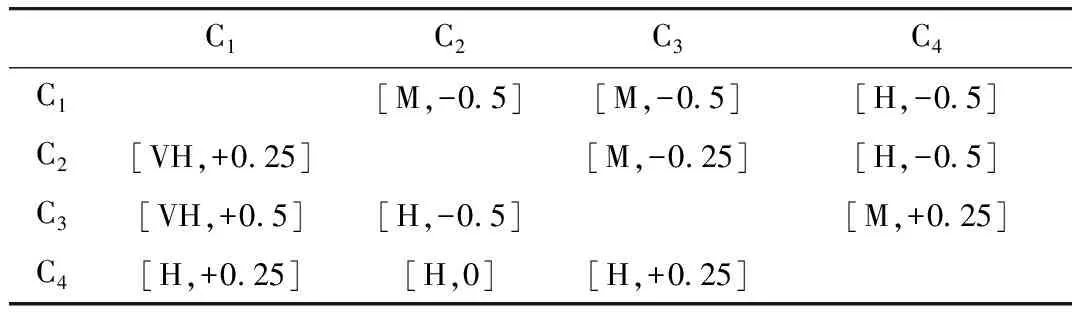
EGH(少于sj)={sr|sr∈S且sr EGH(多于sj)={sr|sr∈S且sr>sj} EGH(至少sj)={sr|sr∈S且sr≥sj} EGH(至多sj)={sr|sr∈S且sr≤sj} EGH(在sj和st之间)={sr|sr∈S且sj≤sr≤st} (1) 2.1.2 获取HFLTS对应包络 (2) 以算数平均值作为语言变量集成算子,通过式(3)确定悲观和乐观偏好关系。 (3) 式中:β∈[0,μ]表示S={si:i=0,1,2,…,μ}经聚合后得到的结果值,可由Δ:[0,μ]→S×[-0.5,0.5)转换为二元性质的语言含义信息,如式(4)所示。式中,round表示为四舍五入后的取整算子。反之,令(si,α)为二次计算语言含义的信息,存在Δ-1函数得到对应数值β∈[0,μ],如式(5)所示。 (4) Δ-1(si,α)=i+α=β (5) 2.1.4 求解指标权重 对于n个风险指标,建立集合矢量VR,有 (6) 设有一个非空集合X,则H={[x,hH(x)|x∈X]}为X上的犹豫和模糊型集合,其中hH(x)表示对于x∈X的隶属度可能值集合且hH(x)⊆[0,1]。 2.2.1 统计犹豫模糊评估集 2.2.2 计算各项指标分值S(hi) 选取犹豫模糊加权平均算子计算各项指标分值S(hi)(i=1,2,…,m)。 (7) (8) 通过HFWA算子,将各指标的犹豫模糊评估集fij进行集成,计算各指标分值s(hi),最终得到分值集合F=(f1,f2,…,fn)。 2.2.3 计算评估结果S S=W×FT=(w1,w2,…,wn)(f1,f2,…,fn)T (9) 本文采用“低度风险”“较低风险”“中度风险”“高度风险”“极高风险”5个等级对大跨径斜拉桥上部结构施工安全风险进行评估,如表3所示。通过计算得到的结果S可以找到与之相对应的施工安全风险评估等级,其数值越大,说明大跨径斜拉桥上部结构施工安全风险越高。因此可以根据S的评估值对施工中的关键风险因素采取风险防范手段,避免发生事故。 表3 风险评估等级 本文以某大跨径斜拉桥为例,邀请4位长期从事桥梁研究的专家。已知所邀专家在该领域的专业背景与工作年限相近,因此设专家权重相同。 1)构建犹豫模糊语言判断矩阵 基于表2与式(1)所定义的规则,专家组利用所提供的语言术语集,对表1所示一级指标进行评估,给出犹豫模糊语言判断矩阵如表4所示。 表4 HFLTS对应包络 2)获取HFLTS对应包络 运用式(2)求得每个HFLTS的对应包络,如表5所示。 表5 HFLTS对应包络 3)确定悲观和乐观偏好关系 表6 悲观集体偏好关系 表7 乐观集体偏好关系 4)确定指标权重 利用式(6)汇总表6和表7中各指标的悲观和乐观集体偏好关系,得到相应的语言区间向量。基于表2为语言变量赋值,计算各数值区间中值,并对结果进行归一化,最终得到一级指标权重如表8所示。 表8 指标的重要性程度 同理,可计算二级指标权重,结果为 W*={0.051,0.057,0.070,0.059,0.058,0.077,0.058,0.070,0.064,0.058,0.068,0.059,0.056,0.058,0.065,0.072}。 1)统计犹豫模糊评估集 专家组基于表3对大跨径斜拉桥上部结构施工安全风险给出评分,即hH(x)={0,0.1,0.2,…,0.9,1.0},分值越高表示该指标的质量越高,最终得到犹豫模糊集评分结果,如表9所示。 表9 安全风险评分 2)计算各项指标分值 已知专家权重相等,因此运用式(7)中的HFWA算子集成评分结果时默认专家权重为 w={0.25,0.25,0.25,0.25}T 得分过程如下(以C11的得分s(h1)为例)。 {0.477,0.539,0.5,0.56,0.505,0.564,0.527,0.584} 基于式(8)计算得分S(h1)=0.532 061。 同理求得,二级指标所有的数据得分,如表10所示。 3)计算评估结果 结合各指标权重,将表10中各指标的分值代入式(9),计算得到大跨径斜拉桥上部结构施工安全风险一级指标评分结果分别为0.344、0.671、0.818和0.662,进而求解目标层最终评分为0.651。 对应表3中的评估等级可知,该桥上部结构施工安全风险评估结果为高度风险,故各部门应该对该桥上部结构施工予以高度重视。 表10 指标算子集成及得分 由表10可知,该桥上部结构施工过程中,16个二级风险指标发生的概率排前三的是:人员意外坠落、张拉不足或超张拉、桥面吊机倾覆坠落,这与桥梁建设中的频发安全风险事件基本相符。为有效预控风险损失,现针对以上关键风险因素的风险控制措施提出几点建议: (1)针对人员意外坠落:①落实安全技术交底,将可能出现的危险和注意事项清楚地告知操作员;②确保施工人员身心状况良好,避免疲劳作业。 (2)提高索导管定位精度,精确控制拉索的张拉力。加强对拉索、锚具、锚箱等产品的质量监测,提高产品的整体质量,减少保管损耗。 (3)针对桥面吊机倾覆坠落:①严格执行吊机荷载试验;②制定半空中突发风振的紧急预案措施;③加强操作人员的专业培养;④加强现场对轨道梁固定状态的监测,防止因轨道梁不牢导致吊机倾覆。 大跨径斜拉桥正向着更大跨径的目标不断发展,而与之相对应的施工安全风险管理理论也需随之发展。本文基于桥面施工、支架施工、钢箱梁施工和斜拉索施工4个方面构建了大跨径斜拉桥上部结构施工安全风险评估指标体系,在此基础上,考虑到决策者在处理复杂问题时存在的犹豫性和不确定性,将基于犹豫模糊语言集的多准则群决策方法用于大跨径斜拉桥上部结构施工安全风险评估,研究结果与实践相符,具有可行性和实用性,且在一定程度上降低了专家主观认知对评估结果的影响,缓解了传统模糊语言在决策过程中的精度损失,拓展了犹豫模糊语言集在桥梁上部结构施工安全风险评估研究领域中的适用范围,为今后相关方面的安全风险评估提供了参考借鉴。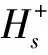





2.2 基于HFWA的风险评估模型



3 实例分析
3.1 HFLTS-AHP方法计算指标权重





3.2 HFWA方法确定综合评分


3.3 风险控制措施

4 结 语

