一种基于等效采样的周期信号谐波分析方法

陈砚圃周 俊解云虹丁海洋

（1.西京学院计算机学院，西安 710123；2.陆军航空兵学院陆军航空兵研究所，北京 101121；3.国防科技大学信息通信学院，武汉 430030）

1 引 言

周期信号是人类活动中广泛存在和广为应用的一类信号。 周期信号的谐波分析是信号分析的基本内容，是对各类信源设备的识别、状态分析及故障诊断的基础。 理论上，如果能够在整数个周期内对信号进行同步和均匀采样，通过离散傅里叶变换（DFT）即可实现周期信号的无误差谐波分析。 但由于信号频率的变化，且采样间隔又只能取定时时钟周期的整倍数，实际中难以做到与整数个信号周期同步的均匀采样。 基于信号采样的谐波分析主要有双速率采样、同步采样、准同步采样和频谱插值等多种方法。 同步采样法须引入硬件倍频电路。 双速率采样法可以消除采样时间在采样过程中的误差积累，但随着信号频率的变化1个周期内的采样点数不固定，不能直接利用2 的整数次方个点的快速傅里叶变换（FFT）进行快速计算。 准同步采样无需精确获取信号频率，但需采用窗函数对多个周期的采样数据进行加权，以抑制不同步采样导致的各谐波间的泄漏干扰。 由于不同的窗函数对应不同程度的谐波泄漏，为此人们设计了众多优异的窗函数用于周期信号的谐波分析。 基于准同步采样的谐波分析还存在栅栏效应，即使进行谱线的插值补偿，由于谐波泄漏在各次谐波上呈不均匀分布，小幅谐波很容易被较强的谐波泄漏所淹没。 采样过程还需满足奈奎斯特采样定理，但实际中对信号的采样间隔必须大于采样保持与模数转换时间，因而极大限制了谐波分析时信号的频率范围。

针对现有谐波分析法存在谐波泄漏不均匀以及有效分析信号的频率范围受采样保持与模数转换时间的限制等问题，利用周期信号的周期性，提出一种结合准均匀采样的等效采样谐波分析法。准均匀采样用于抑制时间离散过程中定时时钟周期对同步采样的影响，等效采样用于突破采样保持与模数转换时间对分析信号频率范围的限制。

2 等效采样谐波分析理论

时间连续形式的周期信号三角函数展开形式为：

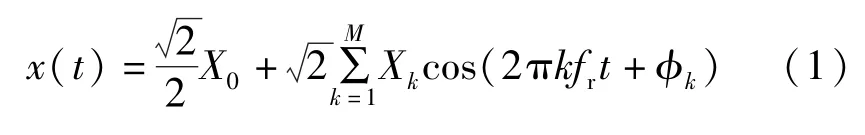
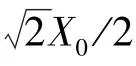
在1 个周期内对信号进行等份均匀采样，采样间隔为＝／，得离散时间序列为：

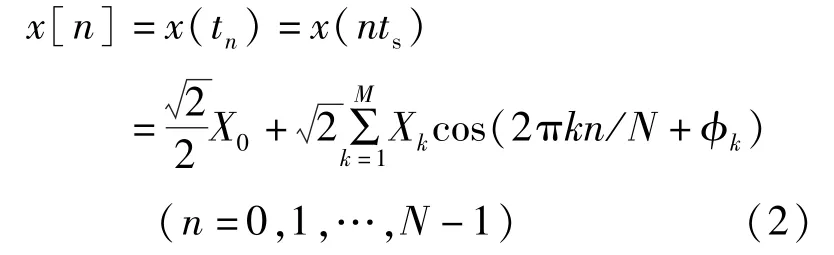
当1 个周期内均匀采样的点数大于2时采样满足奈奎斯特采样定理，信号的复谐波系数可通过［］的严格给出：

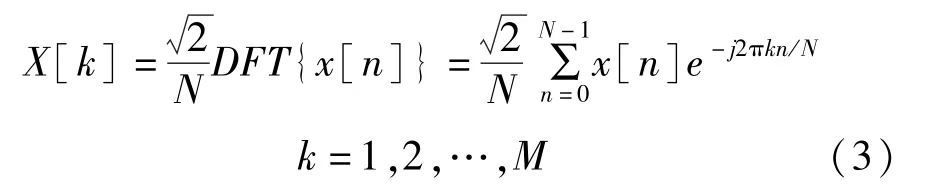
信号第次谐波的幅度和相位分别为：

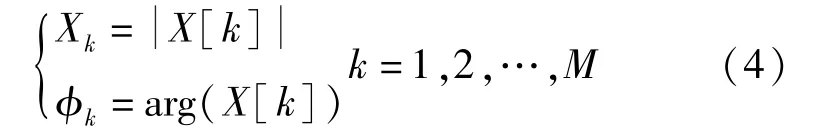
在信号的时间离散过程中，采样保持与转换是需要时间的，只有在上次采样结束后才能启动新的一次采样。 因而采样间隔不能小于采样保持与模数转换时间，即＞。 对采样间隔的这一要求进一步将限制分析信号的频率不能过高，具体为＜（）。 为了拓宽分析信号的频率范围，必须突破采样间隔不能小于采样保持与模数转换时间这一要求。 为此将1 个周期内的次采样分散在多个（整数个）周期内进行，这样无论信号频率多高，只要采样所分散的周期数足够多就能满足＞的要求。 而且利用信号的周期性，在多个周期内的各个采样均可等效为1 个信号周期内的采样，故称为等效采样。 将次采样等效至1 个周期后，只要各等效采样的时间互不相同且等效采样间隔为＝／，则仍可基于式（3）和式（4）进行准确的谐波分析。 显然，等效采样间隔可以小于采样保持与模数转换时间，这自然也就拓宽了分析信号的频率范围。

进一步对完成1 次谐波分析的等效采样限定如下：使用的信号周期数（）为奇数，且应尽可能小；所进行的均匀采样的次数（）为2 的整数次方。这样就有和互质，可以确保在1 个周期内的等效采样的采样间隔为＝／且时间互不相同。 另外，取2 的整数次方可使在分析中能直接利用FFT 进行快速计算。 通常取固定值，下面基于信号周期、采样保持与模数转换时间确定谐波分析中所用的信号周期数以及次采样在1 个周期内等效后的采样序列。

为使实际采样间隔不小于采样保持与模数转换时间，次采样至少要用到的信号周期数为：

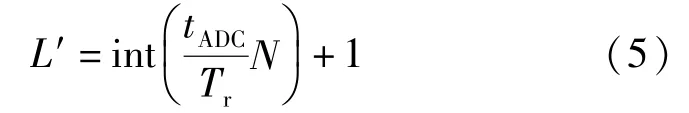
式中：int（·）——截尾取整函数。

为了保证在1 个周期内的个等效采样时间互不相同，取奇数个信号周期：

最后的实际采样间隔为：

在信号的离散过程中，各采样时间均为等效采样间隔＝／的整数倍。 实际采样点的时间序号以步长递增，即＝0，，2，…，（－1），对取余即可得到一周期内个等效采样点的时间序号为：

一周期内的等效采样序列为：

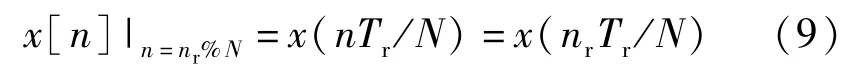
式中：＝0，1，2，…，（－1），对应一周期内个不同的等效采样时间。

通过将个周期内的采样等效至1 个周期，突破了采样保持与数模转换时间对分析信号频率上限的限制。 进一步将式（9）代入式（3）和式（4），理论上可实现信号的无误差谐波分析。

上述信号的时间离散过程中，要求采样为对个信号周期进行等分的均匀采样（等间隔采样）。但实际中对采样时间的控制是由单片机的定时器完成的。 因为定时器工作时的时钟周期（定时时钟周期）为常数，而且采样间隔只能取的整数倍，所以实际的采样间隔一般不会恰好等于式（7）给出的理论值。 如果均匀采样时的采样间隔存在误差，采样时间误差的连续积累会使次采样的时间不等于个信号周期，因而导致非同步采样。 非同步采样会给谐波分析带来谐波泄漏误差与栅栏效应误差。 虽然可以选用窗函数对信号加权以及在频域进行插值补偿对谐波泄漏和栅栏效应进行抑制，但需借助更多的采样数据，且计算复杂度高。 另外信号加窗后的频谱泄漏在各次谐波上的分布不均匀，不利于对小幅谐波的检测与分析。

为了消除采样时间误差的积累，另一种方法是在采样过程中动态调整采样间隔，使次采样的时间等于个信号周期以实现同步采样。 显然该方法中各采样间隔不再相等，因而不属于均匀采样。但由于单片机的定时时钟周期很小，各采样间隔非常接近均匀采样时的值，故将该采样称为准均匀采样。 准均匀采样易于实现且谐波的分析误差在各次谐波上呈均匀分布，特别适于对小幅谐波的分析。

采用结合准均匀采样的等效采样法对周期信号进行谐波分析。 在信号频率以及定时时钟周期已知的条件下，通过单片机定时器触发的在（奇数）个周期进行（2 的整数次方）次采样的实际采样时间为：

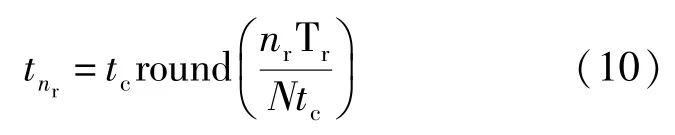
式中：＝0，，2，…，（－1）；round（·）——四舍五入取整。

由此得到的实际采样时间相对于采样时间的理论值存在±／2 以内的时间偏移，采样不是严格的均匀采样。 但实际采样时间的误差不会随连续采样而积累（总在±／2 之内）。

基于式（10）得到的各离散时间用于触发周期信号的采样，再将采样结果代入式（8）、（9）得到一周期内的等效采样序列。

3 谐波误差分析

实际的采样过程中，时间离散与采样中的幅值量化均会给谐波分析带来误差。 基于式（10）给出的采样时间在个信号周期内进行次采样后，在1 个周期内的等效采样序列可表示为：

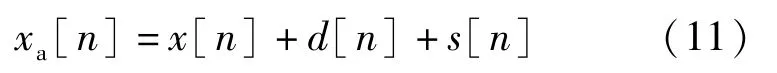
式中：［］，［］——时间离散和幅值量化引入的误差序列。

对式（11）做DFT，得次谐波的复谐波系数为：

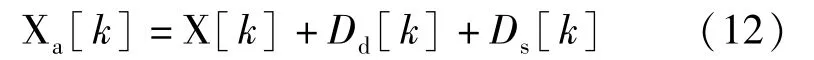
时间离散误差序列的一阶近似为：

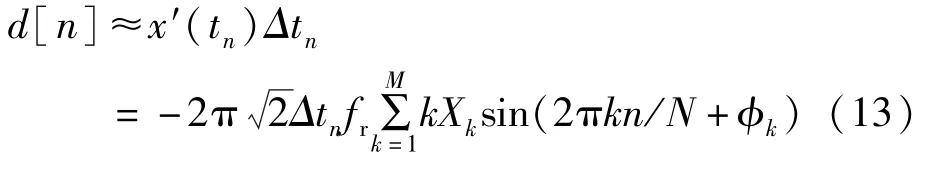
式中：Δt——采样时间误差。

实际中，基波的幅度通常远大于其他诸次谐波的幅度。 作为近似仅计入基波对时间离散误差序列的贡献，则有：

时间离散误差序列［］的复DFT 系数［］为：

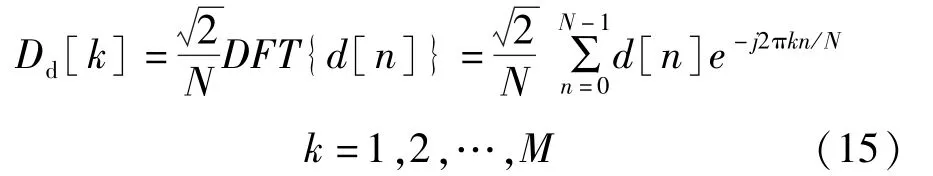
［］由式（14）近似给出，可导出［］的标准差为：

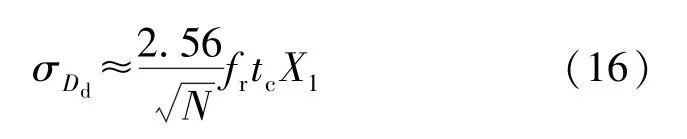
此标准差用于表示信号采样中时间离散引入的谐波分析误差。 同样，幅值量化误差序列［］的复DFT 系数［］为：

设信号采样中幅值量化的结果为位的2 进制数，工程中通常将信号的最大动态范围设为其额定峰峰值的120%。 进一步对信号做基波近似，并以表示信号有效值的额定值，则时域信号幅值量化步长为3.4 ×2 X。 再利用采样中幅值的量化误差在±1.7 ×2X之内近似服从均匀分布，［］近似服从均值为0 的正态分布，可导出［］的标准差近似为：

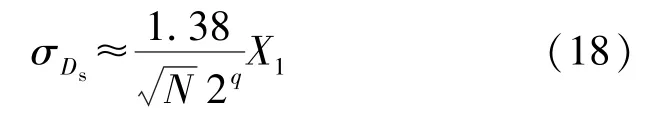
此标准差用于表示信号采样中幅值量化引入的谐波分析误差。

实际的采样过程中非均匀时间离散和幅值量化并存，误差序列的复DFT 系数为［］＝［］＋［］，综合标准差为：

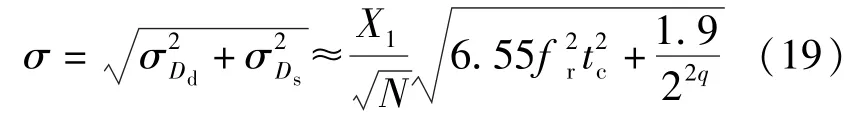
当＜＜X时，第次谐波的相位的平均误差近似为：

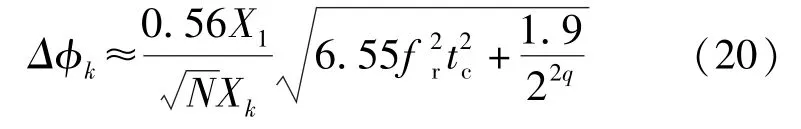
可以看出，时间离散和幅值量化引入的综合谐波误差在各次谐波上呈均匀分布，与谐波的次数无关；提高定时时钟频率（＝1／）和幅值量化位数（）均可有效提高谐波分析的精度；分析信号的频率越高，谐波分析的误差也就越大。

4 等效采样谐波分析算法

为了在计算中能够直接利用FFT 进行快速计算，取2 的整数次方。 基于信号周期以及信号的采样保持与模数转换时间，由式（6）计算出进行次等效采样所用的最小奇数周期数。 如此，由式（9）导出一个信号周期内在时间上互不相同的个等效采样值。

对信号的等效采样中，采样时间通过单片机的定时器进行触发控制。 为了使离散采样时间在滚动更新中尽可能精准和计算简捷，程序中的采样时间累加和、采样间隔等量均采用长整型变量表示。只要代表采样间隔的整型变量的2 进制位数足够长，次采样后的时间积累误差就可以忽略不计，实际采样就可视为与信号周期同步。 单片机定时计数器常用的工作模式中，自动重装递增、自动重装递减以及循环递增等模式均可用于触发准均匀采样。 设所用定时器中的工作计数器由个2进制位组成，定时时钟周期为。 这里采用循环递增的连续计数模式，当连续递增到预设计数值时会自动触发一次采样。 为了方便，算法中用到的长整型变量有：由个2 进制位组成的采样时间累加和，用于记录滚动更新的采样时间；采样时间累加增量；触发采样的预设计数值。

与采样间隔对应的采样时间累加增量为：

为对／放大取整后的整数，其低位对应／的二进制小数。 只要选的足够大，由累加得到的就足够精确。 采样触发预设计数值取自的高位，每当递增到与相等就立刻触发一次采样。

将准均匀采样与等效采样相结合，周期信号的谐波分析流程如下：

1）初始化：

复位采样时间累加和：＝0；

设置采样时间累加增量：＝int（（2）∗∗／（∗））；

复位采样序号：＝0；

复位定时计数器：＝0；

启动定时计数器。

2）触发一次采样；

3）设置定时器下一次触发采样的计数值：

＋＝；

＝round（／（2）。

4）等待采样保持与转换的结束；

5）保存本次采样结果：

＝%；

［］＝采样结果；

＝＋。

6）等待采样触发事件发生（＝）；

7）若采样不足次，转（2）；

8）完成一次谐波分析：

对等效采样序列［］（＝0，1，2，…，－1）做FFT；

计算1 ～次谐波的幅度和相位。

多数单片机定时器的工作计数器为16 位（＝16），若和均选为32 位（＝32）整型变量，并设＝16，则采样间隔可精确到1.5 ×10的数量级，次连续采样的时间积累误差可以忽略。为使计算简单、高效，算法中控制采样时间的变量均采用了整形变量。 另外取每周期内的等效采样点数的值为2 的整数次方，以便直接利用FFT 进行快速计算。

5 数值仿真与结果分析

实验信号由6 个谐波（含基波）分量组成，具体参数如表1所示。 其中主要成分基波的有效值为1 000 mV，最小的谐波幅值仅为1 mV，最高谐波次数为49。 实验中单片机的定时时钟周期＝1 μs、采样保持与模数转换时间＝1 μs、1 个信号周期内的等效采样点数＝128。 引入相对于定时时钟频率的归一化频率＝／作为控制变量，实验中分别改变归一化频率和信号模数转换时幅值量化位数，谐波分析误差为采样起点随机给出时测量误差的统计平均。

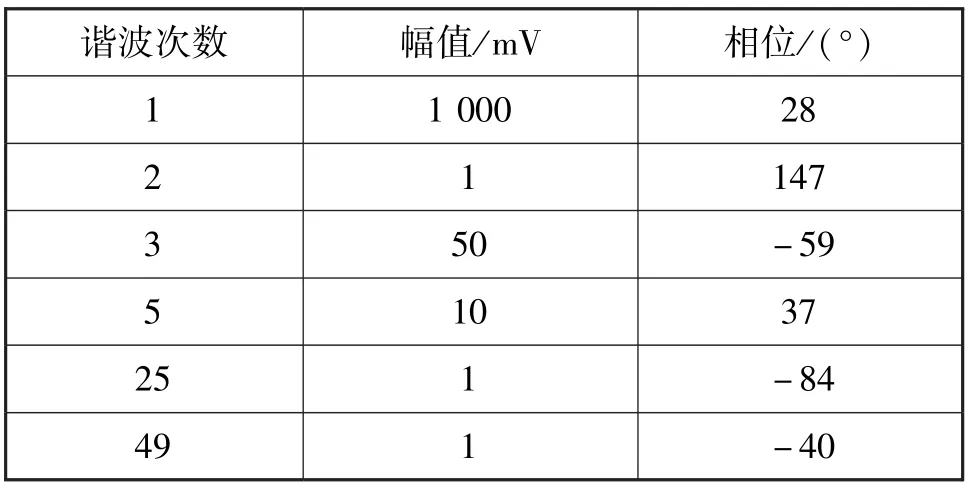
表1 实验信号的参数Tab.1 Parameters of experimental signal

不考虑信号幅值量化而仅改变归一化频率时，各次谐波测量中幅值的标准差和相位的平均误差，如表2和表3所示。 从表2可以看出：同一列中的数据近似相同，验证了谐波幅值的标准差不随谐波次数的变化而变化；谐波幅值的标准差正比于归一化频率，与式（16）的结果（0.022，0.113，0.226，1.131）非常吻合。 由表3的数据可知：归一化频率一定时，信号谐波的幅值越小，相位估计误差就越大；当归一化频率增大时，相位估计误差也随之增大。

表2 不同归一化频率对应的幅度标准差Tab.2 Amplitude standard deviations of different normalized frequencies mV

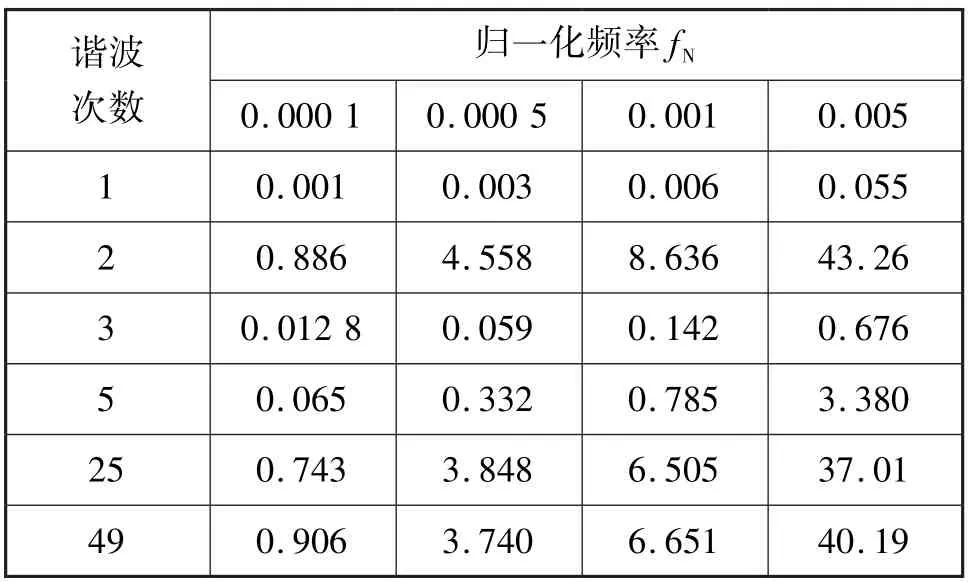
表3 不同定时时钟周期对应的相位平均误差Tab.3 Phase average errors of different timing clock cycles （°）

不考虑信号的非均匀采样而仅改变信号的幅值量化位数时，各次谐波测量中幅值的标准差和相位的平均误差，如表4和表5所示。 从表4可以看出：同一列中的结果非常接近，说明谐波幅值的标准差不随谐波次数的变化而变化；谐波幅值的标准差反比于2，且与式（18）的结果（0.476，0.119，0.030，0.002）非常吻合。 由表5的数据可知：幅值量化位数一定时，信号谐波的幅值越小，相位估计误差就越大；当幅值量化位数增大时，相位估计误差则随之减小。

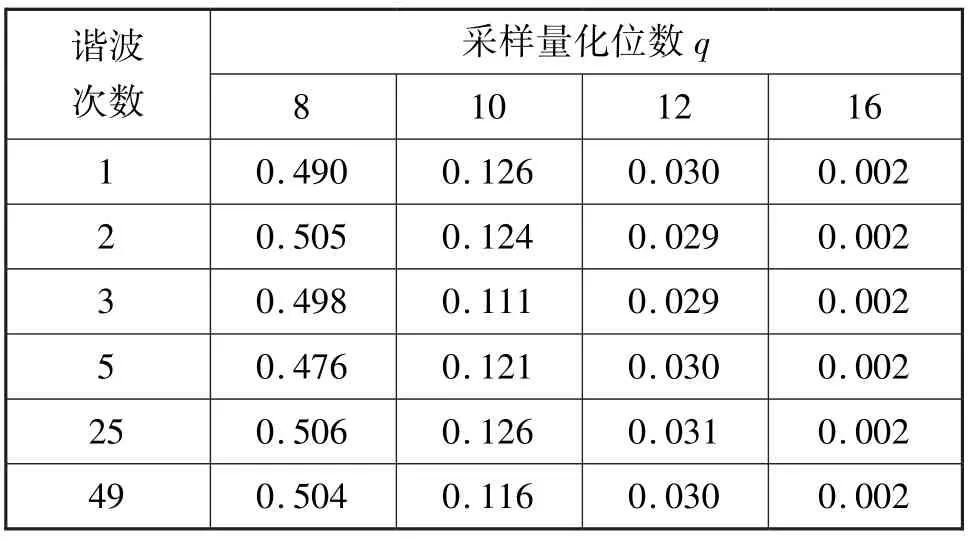
表4 不同采样量化对应的幅度标准差Tab.4 Amplitude standard deviations of different sampling quantization mV

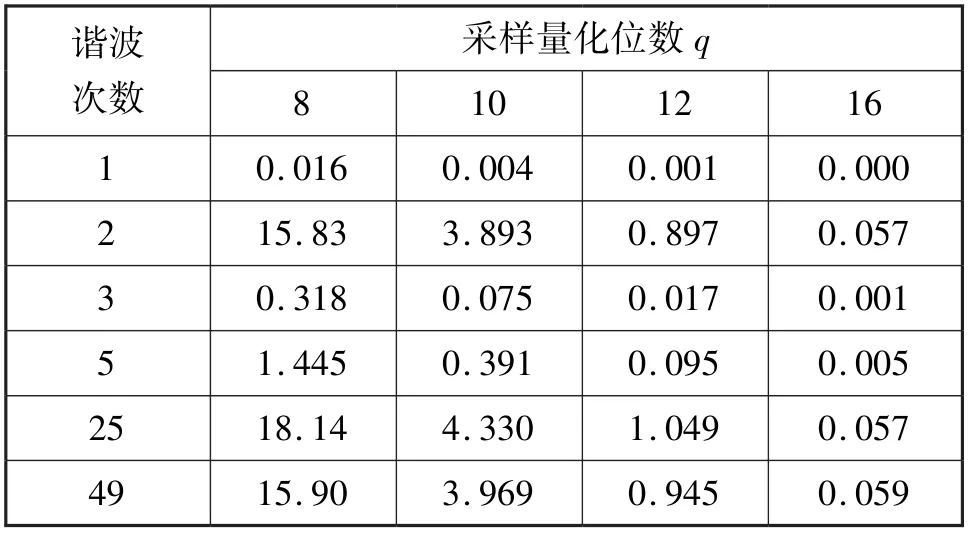
表5 不同采样量化对应的相位平均误差Tab.5 Phase average errors of different sampling quantization （°）

以上在采样点数、采样保持与模数转换时间以及定时时钟周期取一组典型值的条件下，分别改变信号的归一化频率和幅值量化位数对等效采样谐波分析法进行了数值仿真。 实际中的值取2 的整数次方且大于信号最高谐波次数的2倍。 虽然理论上等效采样谐波分析的精度与的取值无关，但对可编程配置的数模转换器，可适当配置较大的值，以提高信号的采样保持和量化的稳定性。 定时时钟周期由所选的单片机系统决定，通常在（0.01 ～10）μs 范围内取值。 定时时钟周期越小，谐波分析越精确。

应用中还需明确等效采样用于有效谐波分析时分析信号的频率上限。 实际上分析信号的最高频率由信号中的最高谐波次数、定时时钟周期、信号幅值量化位数，以及需满足的分析精度等因素综合决定。 如对表1给出的最高谐波次数＝49 的分析信号，若要求谐波幅值和相位误差分别小于0.3 mV 和5 °，则其他参数需满足＝128，≤0.000 5，以及≥10。 若取＝0.01 μs，则分析信号的最高频率为50 kHz。 如果仅把归一化频率范围拓宽至≤0.001而不改变其他参数，分析信号的最高频率可提高至100 kHz，此时谐波幅值较大的1 次、3 次和5次谐波仍满足精度要求，但谐波幅值仅为1 mV 的2次、25 次和49 次谐波已不能有效分辨。

6 结束语

提出了一种结合准均匀采样对周期信号进行等效采样实现谐波分析的方法，突破了信号的采样保持与模数转换时间对分析信号频率的限制；对等效采样谐波分析的误差进行了分析，导出了各次谐波幅值和相位的误差公式；给出了等效采样谐波分析的具体流程。 借助含有多个小幅谐波分量的实验信号对等效采样谐波分析进行了数值仿真，验证了理论和算法的有效性。 理论分析和仿真实验均表明，所提出的等效采样谐波分析方法拓宽了可分析信号的频率范围；时域准均匀采样和幅值量化所带来的误差在各次谐波中呈均匀分布，特别有利于对小幅谐波的检测；在1个周期内的等效采样点数总能取2 的整数次方，算法可以直接借助FFT 快速实现；算法中动态控制采样时间的各变量均取为长整型变量，计算精准且简捷。所提出的等效采样谐波分析方法特别适用于自带模数转换的单片机嵌入实现，无需其他硬件开销。