基于遗传算法化工领域往复压缩机故障诊断分析
何奋彪
(中国石油兰州石化公司 化工运行一部,甘肃 兰州 730060)
在石油化工领域,往复压缩机是一种十分重要的机械设备类型,可以实现对各种气体的高效压缩和输送,满足人们生产过程中的各种需求。往复压缩机具有十分复杂的结构,激励源众多,其轴承较易出现各种故障,影响到设备的正常运行,也给实际生产造成了一定的影响。但是,在往复压缩机的工作和运行过程中,可能会出现一定的故障,进而影响到生产的效率以及安全性。为此,针对往复压缩机,还需要重视相关的故障问题,并做好准确的故障诊断,以及时排除故障,确保高效、安全生产。实践工作中,还需要提高对往复压缩机轴承故障的重视程度,并积极地做好相应的故障诊断工作。
1 VMD与基于遗传算法的VMD参数优化
变分模态分解(VMD)具备强大的信号处理能力,可以对多种不同类型的信号予以有效的处理,例如各种具有非平稳性、非线性特征的信号;同时,VMD还具有较强的噪声敏感性。在处理各种信号的时候,VMD可以对信号分量的获取过程进行一定的转移,将其转移到变分框架内,并进行合理的处理。在处理过程中,可以科学的分解原始信号,避免各种问题的出现,提高原始信号的分解效果,具有较好的复杂数据分解精度及较好的抗噪声干扰等优点。但是,VMD存在一定的不足之处。VMD对信号的分解层数和惩罚因子需要采用人为方式进行选取;惩罚因子和分解层数K的具体选择情况会对VMD方法的最终分解效果产生极大的影响。同时,采用相应的参数设置方法也无法获得最优的参数组合,无法很好的满足实际分析研究的需求。为此,在本文的研究中,选择依托遗传算法进行必要的参数优化。应用遗传算法法对VMD 算法进行参数优化,可以实现对带宽参数以及分解层数的优化处理。在优化处理时,可以使用适应度函数对目标函数在解空间进行全局并进行随机搜索,以获得优化参数。变分模态分解参数优化过程中,首先需要结合实际需求,对适应度函数进行建立。之后,通过随机方式形成初始化阶次种群。并以一定的种群条件为背景,对相关的信号实施VMD分解,并对不同种群个体的适应度进行计算。计算结束后进行分析,如果满足了实际的终止条件,则在输出最优结果之后完成整个参数优化。另外,也可以针对实际需求进行一定的选择、变异和交叉处理,得到新的种群。之后,与终止条件进行对照分析,如果满足条件的要求,则在输出最优结果之后完成参数优化过程。
2 多尺度散布熵
本次研究中使用遗传算法研究得出VMD算法的最佳影响参数组合,对相关的带宽参数以及分量个数等进行研究,得到分解故障信号。之后,对分解后的BLIMF 分量峭度值进行计算,并通过筛选,得出最佳BLIMF 分量,实现对故障信号的重构。在散布熵基础上,可以提出多尺度散布熵(MDE)。多尺度散布熵可以实现对时间序列复杂性的有效度量,相关的时间序列越复杂,新模式产生的可能性便越高。这一情况下,可以对样本熵进行有效的扩展,将其扩展到多个不同的时间尺度。之后,便可以结合实际需求,在时间尺度不确定的情况下,获得额外的观察视角。在计算的时候,散布熵在全程应用的参数是基于正态累积分布函数映射(NCDF)的数据平均值与标准差。在具体的计算中,上述2个参数均被设置为原始数据的平均值和标准差,在所有尺度上,则保持不变的状态。往复压缩机的振动信号具有非线性特征,对于设备不同位置的故障状态,在所具备的特征方面,相互之间也呈现出非线性关系。具体来看,在具体计算多尺度散布熵的时候,可以按照以下的方式完成计算:
(1)设定一定的信号,将其长度设置为,具体计算公式:
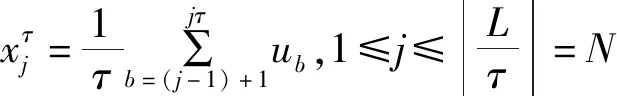
(1)
(2)参照不同尺度因子的具体情况,计算相应粗粒化信号下的散布熵值,计算公式:
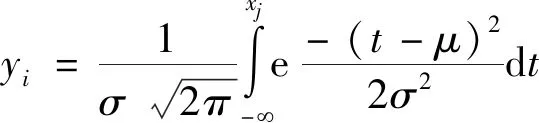
(2)
式中:、分别代表的是时间序列的标准差、均数。按照上述公式计算完毕后,可以应用线性算法将分配到有一定范围内的任意整数,并获得相应的映射信号,具体计算公式:
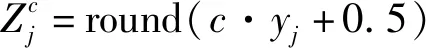
(3)
在这一过程中,应用了线性方法,但因为在计算中使用NCDF 进行了映射,因此从整个映射过程来看,属于非线性过程。
在时间序列方面,可以使用延迟时间和嵌入维数来构成这一序列,具体计算公式:
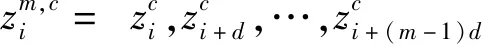
(4)
在具体的计算过程中,需要考虑到时间序列的映射情况。在计算中,所有的时间序列都会被映射到一定的分散模式之中。信号具有不同的类型,数量以“” 表示。不同的信号类别均为整数,相应的取值范围为1~。在上述条件下进行分析,不同时间序列所分配的分散模式数量便可以用“”来表示。分析不同的潜在分散模式,可以对其相对频率进行计算,具体的计算公式:
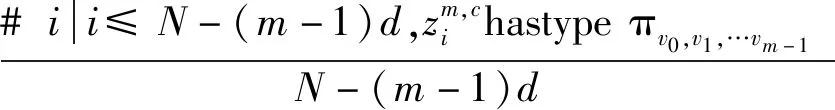
(5)
在计算完毕后,结合计算结果以及信息熵的定义,可以实现对散布熵值的具体计算,计算的方法为:
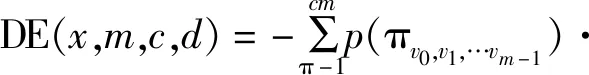
(6)
结合计算所得的结果进行分析,可以得出不同尺度因子下的MDE 定义,具体计算公式:
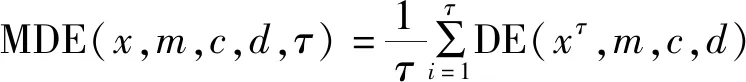
(7)
3 VMD 和MDE 的参数优化
3.1 往复压缩机轴承故障诊断总体方法
在对往复压缩机轴承故障进行诊断的时候,还需要对往复压缩机的特点进行全面的分析。通过分析可以了解到,往复压缩机的轴承振动信号具有显著的复杂多分量耦合特点。因此,在本文的研究过程中,选择以参数优化的VMD和MDE为依托,分析相应的轴承故障诊断方法。在诊断过程中,首先需要应用遗传算法来对VMD方法实施参数优化,以得到最佳的优化参数组。针对实际诊断研究的需求,对这一优化参数组进行合理的设置,将其设置为VMD分解参数。之后,合理的分解往复压缩机轴承故障信号,并得到若干个BLIMF分量。之后的步骤中需要对不同BLIMF 分量对应的峭度值进行计算,比较分析计算所得到的数据结果,从中选择出可以显著体现轴承故障特征的BLIMF 分量。将这些BLIMF分量实施重构,获得所需的故障信号。整理重构后获得的故障信号,实施MDE分析。对于重构后得出的故障信号MDE 熵值进行量化计算,获得往复压缩机轴承故障特征向量。之后,开展一定的训练和测试活动,以获得最终的诊断结果。这一过程中,可以使用的仪器为极限学习机(ELM),应用该仪器,可以实现轴承故障特征向量的针对性训练和测试,并最终获得所需的结果。
3.2 遗传算法下的往复压缩机轴承故障诊断案例分析
为更好的研究遗传算法下的往复压缩机轴承故障诊断方法,在本文中,我们结合一定的实际案例进行分析研究。选择以某型号往复压缩机为例,开展轴承故障模拟实验,相应的轴承故障形式为一级、二级连杆大小头处轴承间隙大。在实验过程中,首先对缸体表面一级、二级连杆大小头处的振动信号进行采集,应用的仪器为加速度传感器。在信号采集过程中,相应的采样频率设定为50 kHz,采样时间设定为4 s。在分析的时候,需要对研究中的相关参数进行确定,涉及到的参数主要为带宽参数以及VMD分量个数。其中VMD分量个数是通过应用一定的算法对VMD进行分解得到的,此次研究中选择使用的算法为遗传算法。通过遗传算法可以优化不同轴承振动信号的VMD 分解参数,采用优化后的VMD 参数设置,分别针对一级连杆小头轴承间隙偏大或者二级连杆大头轴承间隙偏大等不同的故障状态信号进行分解,并得出具体的参数数值结果。在本章节的研究中,经分析和计算,得出的不同故障状态下振动信号VMD相关参数大小情况如表1所示。
结合表1中的参数情况,按照对应的VMD 参数设置,分别对不同轴承正常以及4种不同轴承故障类型下的5种状态信号实施分解。分解结束后,通过计算得到不同BLIMF 分量所对应的峭度值,不同状态振动信号下轴承不同BLIMF 分量的峭度值情况如表2所示。

表1 不同故障状态下振动信号VMD相关参数大小汇总Tab.1 Summary of VMD related parameters of vibration signals under different fault states
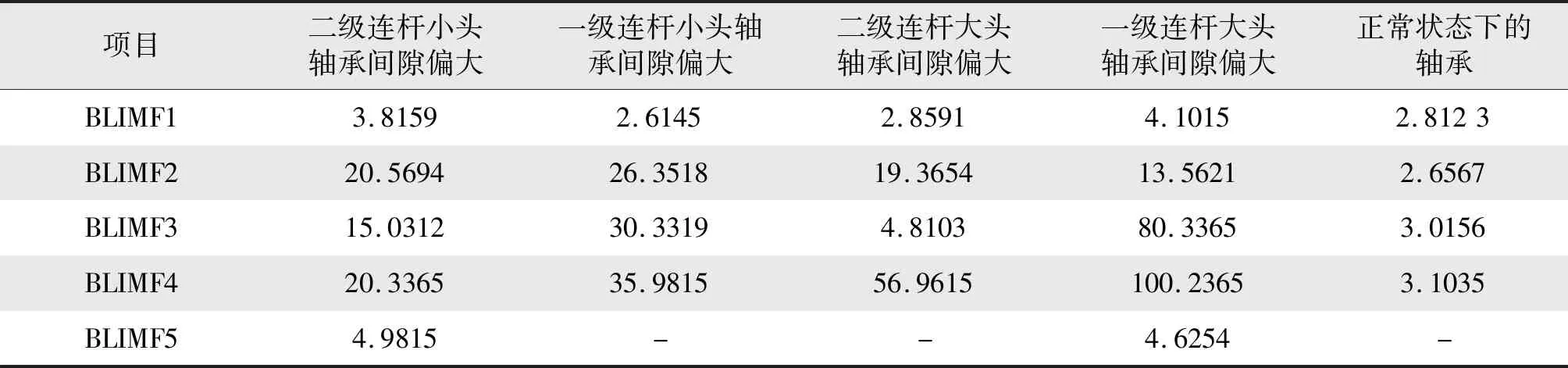
表2 不同状态振动信号下轴承不同BLIMF 分量的峭度值情况Tab.2 Kurtosis values of different BLIMF components of bearings under vibration signals of different states
在故障诊断过程中,峭度值越大,所对应的信号中所含有的故障成分就越多。由此进行分析,可以通过比较,将其中峭度绝对值较大的BLIMF 分量筛选出来,并针对这一分量实施信号重构,以实现对不同状态下信号的分析研究。结合表2 中的数据结果进行研究,可以了解到,如果往复压缩机的轴承处于间隙偏大的故障状态时,其中一些BLIMF 分量所对应的的峭度值则会出现异常变化,表现出显著增大的情况,数值远远高于3。如果往复压缩机轴承处于正常状态,结合表2中的数据结果进行分析可知,分量BLIMF3、BLIMF4 所对应的峭度值在3左右,较为接近正态分布。因此,在本次研究中,为了获得理想的诊断效果,选择以正常状态下峭度值在3所有的BLIMF 分量为参照重构信号,对于故障状态下的峭度值,采用远大于3 的BLIMF 分量进行信号重构。之后,可以对轴承不同类型状态重构后振动信号的多尺度散布熵进行计算。
在多尺度熵的粗粒化环节,尺度因子是一个十分重要的指标。在对这一指标进行选择的时候,需要综合考虑多方面情况的影响以及实际需求,从而合理控制尺度因子具体取值的大小,避免出现取值过大或者过小的问题。如果尺度因子具体取值过大,则可能会导致不同信号之间复杂度差异无法得到有效的分析。如果尺度因子具体取值过小,则无法对信号的各种特征信息予以全面的提取。通过计算以及结果分析可以了解到,当尺度小于5 的时候,对应的多尺度散布熵值会呈现出逐渐增大的变化趋势。而随着尺度的不断增大,多尺度散布熵值则会出现逐渐减小的情况。同时,在一定的尺度范围内,轴承不同类型状态下的多尺度散布熵值之间存在十分明显的差异。如果尺度达到8以上,则对应的多尺度散布熵值曲线会出现十分明显的交叉现象。此次研究中,对上述多种情况进行综合性的分析,为获得更为理想的故障诊断效果,采用本文所述方法对轴承5 种状态信号进行分析,构建往复压缩机轴承状态特征向量集。不同特征提取方法下的各种轴承故障状态类型ELM识别率与总识别率如表3所示。

表3 不同特征提取方法下的各种轴承故障状态类型ELM识别率与总识别率Tab.3 ELM recognition rate and total recognition rate of various bearing fault state types under different feature extraction methods
3 结语
在实际生产中,针对往复压缩机这一石油化工行业的关键设备,提高对其轴承故障的关注程度,并积极的做好相应难度诊断是十分重要的。在具体的故障诊断过程中,还需要结合实际情况,进行科学的全面分析,选择更为科学、高效的诊断与评估方法。在本次研究中,提出了基于参数优化VMD 和MDE 的往复压缩机故障诊断方法,使用遗传算法研究得出VMD 算法的最佳影响参数组合,并对相关的带宽参数以及分量个数等进行研究,得到分解故障信号。之后,对分解后的BLIMF分量峭度值进行计算,得出最佳BLIMF 分量,实现对故障信号的重构。同时,还在散布熵的基础上,提出从多个时间尺度下反映时间序列复杂度的多尺度散布熵。分析这一熵值,可以较为全面地观察到时间序列的复杂程度,同时也可以提高算法的准确性。针对重构后得到的故障信号实施MDE分析,并通过极限学习机测验等方式,可以获得相应的故障类型中识别效果。在研究中,还结合具体案例进行了分析,证实了本文所提出的往复压缩机轴承故障诊断和识别方法是有效的,具有一定的实践应用价值。

