动态工况下超声电机转速及效率优化控制方法
蔡春晨,毛雪飞,赵雷,陈振,李震
(北京理工大学自动化学院,北京 100081)
超声电机因其具有低速大转矩、无电磁干扰、断电自锁、响应快、速度和位置控制性好等优点[1],在航空航天、机器人、移动电子设备等运动控制领域得以广泛应用[2]。但由于其独特的机电能量转换方式,超声电机的效率还不是很高[3]。一方面,由于其主要应用场合能量供应有限,过低的效率会严重制约系统的续航能力;另一方面,效率过低意味着机电能量转换过程产生大量的热量[4],导致电机升温,而温度升高对电机的材料、谐振频率、动态特性影响很大[5-7],给电机的高精度、高动态性能控制带来挑战,甚至损坏电机。因此,在实现超声电机转速控制前提下如何最大程度地提升其工作效率已成为此领域内亟需解决的关键问题之一[8]。
超声电机转速及效率优化控制方法研究的重点主要包括:效率反馈方式、控制变量的选择以及动态工况下效率优化算法的稳定性。当调节频率使得电机驱动电压和电流之间相位差的余弦值最大时,可实现效率的间接反馈控制[9-11]。文献[9]仅采用了频率单变量控制,无法同时满足转速和效率的控制需求,不能实现效率的全局优化;文献[10-11]通过引入占空比这一控制变量,在精准控制电机转速的前提下实现最大效率。然而上述方法需要检测电压和电流并计算相位差来实现效率反馈,因此电路复杂、计算量大。以双变量控制为基础,通过只检测电压并将其控制到最小值来跟踪最大效率点,实现了转速和效率优化控制[12]。在实际工程应用中,由于电机的需求转速及负载转矩会发生动态变化,上述方法不能保证效率优化算法的收敛精度和动态工况下的稳定性。
在对超声电机及其驱动电路工作特性分析的基础上,确定电机转速和效率优化两个控制量,然后对基于驱动电压有效值的效率反馈方式进行理论证明,并针对电机的电压-效率-频率特性设计了最大效率点跟踪(maximum efficiency point tracking,MEPT)算法,并基于最小二乘法(LSM)的多项式曲面拟合方法计算得到频率更新步长。
1 超声电机及其驱动电路工作特性分析
针对超声电机的工作原理,驱动电路的常用拓扑主要有三种:推挽电路、全桥电路和半桥电路[13],其中全桥电路在可靠性、输出电压谐波等方面性能最好,因此应用最为广泛。
1.1 全桥驱动电路工作特性
超声电机及全桥驱动电路拓扑如图1所示,其中Udc为直流输入电压,Q1~Q8为开关管MOSFET。

图1 超声电机及全桥驱动电路拓扑Fig.1 Ultrasonic motor and full bridge drive circuit topology
图1中,A,B两相全桥电路均采用移相PWM控制,Q1~Q8的驱动信号频率均为fs,占空比固定为50%(忽略死区),且同一桥臂上、下两个开关管(如 Q1和Q2)驱动信号互补。变压器TrA,TrB变比均为1∶N,其输出电压uA,uB是频率为fs的方波电压。调节左、右桥臂开关管(如Q2和Q4)驱动信号之间的相位差,即可改变uA,uB的占空比D1,其取值范围为[0,1]。调节A相和B相同位置开关管(如Q4和Q8)驱动信号相位差,即可改变两相电压uA,uB相位差α,为保证电机具有较高的电机效率和运行稳定性,一般将α固定为π/2。变压器输出端和超声电机USM两相输入端之间分别串联一个匹配电感LA,LB,电感值均为Ls,主要作用是进行滤波和功率匹配[14],得到正弦交流电压uFA,uFB,于是可以通过全桥驱动电路的两个变量fs和D1改变超声电机驱动电压uFA,uFB的频率和幅值。
1.2 定子行波的产生及定转子接触模型
在超声电机压电陶瓷片上施加电压uFA,uFB,通过逆压电效应可在定子上激发出两个模态响应wA,wB,且满足下式:

式中:Θ,M,C,K分别为机电耦合系数、定子的模态质量、结构阻尼和机械刚度系数。
当D1=1时,模态响应wA,wB获得最大幅值为

式中:Cd为电机等效静态电容。
两个模态响应在定子上叠加形成波长为λ的旋转行波。由于定、转子间存在一定的轴向预压力,它们在行波波峰附近存在摩擦作用,摩擦区域坐标和正、负摩擦分界点坐标分别为xc和xs,由于摩擦作用转子可获得的最大空载转速为[10]
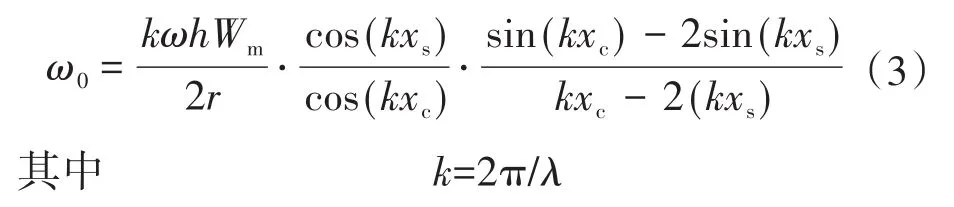
式中:h,r分别为转子的厚度和外径;λ为定子行波的波长。
电机转速为ωR时,转子通过摩擦获得的驱动力矩可用下式表示:

式中:kT为转矩系数。
2 转速及效率优化控制方法设计
超声电机转速及效率优化控制框图如图2所示,外环对电机转速进行采样和比较,经过PI控制器得到控制量D1。内环通过效率间接反馈单元对驱动电压uFA进行整流滤波、采样并计算其有效值UF,利用所设计的MEPT算法计算得到控制量fs。驱动电路在D1和fs的双变量控制下经过匹配电路输出uFA,uFB,进而对超声电机进行控制。

图2 转速及效率优化控制框图Fig.2 Speed and efficiency optimization control block diagram
电机工作时分为两个阶段:阶段1(0—t0时刻),电机从静止开始启动,MEPT算法不起作用,驱动频率fs设为恒定值f0,外环PI控制器正常工作直到转速达到给定值;阶段2(t0时刻之后),MEPT算法由初始值f0开始对fs进行更新,直到采样计算得到的UF值达到最小值,此时电机工作在最大效率点。
2.1 转速控制器设计
设电机转动惯量为J,负载转矩为TL,有:

超声电机的模型可由式(4)、式(5)确定,见图2。当电机达到稳态时,驱动力矩与负载转矩相等,即TR=TL,于是由式(4)可以得到:

采用结构简单、应用广泛的PI控制器,将电机实际转速nR与转速参考值n*R进行比较,得到偏差值E作为控制器输入,经过如下式表示的控制律作用得到的输出值作为占空比D1(s):

式中:KP为比例系数;TI为积分时间常数。
2.2 基于驱动电压有效值的效率反馈方式
基于电压有效值的间接反馈方式简单可靠,下面对此效率反馈方式的合理性进行证明。
机械品质因数Qm是衡量超声电机能量转换性能的重要参数,可由下式给出:

同时有:

电机在最大效率点ηmax工作时,驱动频率设为fm,此时Qm和cosφ达到最大值。由于稳态情况下电机存储的总能量WU为定值,因此由式(8)、式(9)可知此时UF达到最小值,因此UF可作为电机效率的间接反馈量。测得Shinsei USR60型超声电机在90 r/min,0.3 N·m条件下,UF和η随频率fs变化的曲线如图3所示,其中fm=41.72 kHz。

图3 90 r/min,0.3 N·m时UF和η随频率fs变化曲线Fig.3 Variation curves of UFand η with fsunder 90 r/min,0.3 N·m
2.3 效率优化算法设计
基于图3中UF和η随fs变化的曲线特性,一种基本的效率优化的思想是对最大效率点fm进行跟踪:由初始值f0开始,每隔UF的采样周期Tsample按步长Δf减小驱动频率fs,然后计算频率变化前后UF的变化量 ΔUF,若 ΔUF<0,则继续减小fs,否则认为UF达到最小值UFmin,即电机工作在最大效率点ηmax,不再减小fs。频率更新的步长会影响效率优化算法以及转速控制的性能,文献[12]采用分频段变步长的方式,当fs距离fm较远时,设置步长0.3 kHz,距离较近时设置步长0.003 kHz,缩短了优化过程的时间。但上述步长设置方式无法保证算法的收敛精度和动态工况下的稳定性。所提出的MEPT算法如图4所示,基于最小二乘法的多项式曲面拟合方法计算Δf。

图4 MEPT算法流程图Fig.4 Algorithm flow chart of MEPT
工作流程描述如下:
1)对算法中各参数进行设置。
f0为MEPT算法开始执行时刻(t0时)电机的驱动频率,一般大于超声电机谐振频率fr,并保证此频率下D1能够满足常用工况下启动阶段的调速范围60~110 r/min,仿真结果表明43.5 kHz可以满足此要求;p为采样周期数,将UF在连续p个Ts周期内取平均值,用于减少UF在采样过程产生的随机误差,取值过大会降低算法的收敛速度;ΔUmin为电压判断阈值,用于抑制算法在最大效率点附近由于ΔUF在零值上下波动引起的振荡,保证算法的稳定性。经过仿真测试p和ΔUmin分别取21和0.4 V可以满足以上要求。
2)根据UF计算得到。
F(k)计算示意图如图5所示,横轴t代表算法执行的时间坐标,相邻两个时间点的间隔为Tp=p×Ts。在区间[t(k-1),t(k)],[t(k-2),t(k-1)]内,驱动频率分别为f(sk),f(sk-1),二者的差值记为Δf(sk),UF的平均值分别记为二者的差值记为。

图5 F(k)计算示意图Fig.5 Calculation diagram ofF(k)
3)根据电机转速nR和转矩TL,基于最小二乘法的多项式曲面拟合方法计算Δf。
如图3所示,在超声电机工作的最大效率点fm的邻域[fm-δf,fm+δf]内,UF与驱动频率fs之间的关系可使用下式表示的曲线进行精确拟合:
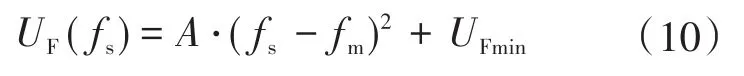
其中,A为二次项系数,是转速nR和转矩TL的函数。若要保证超声电机工作在最大效率点,应保证下式成立:

由式(10)、式(11)联立可得:

为防止算法发生振荡,并保证较高的收敛速度,取式(12)“ = ”成立,并将Δf表示为转速nR和转矩TL的函数g(nR,TL):

Shinsei USR60超声电机常用工作范围为60~110 r/min,0~0.5 N·m,转速和转矩分别间隔 10 r/min,0.1 N·m,选取 36个工况(nRi,TLi),i=1,2,…,36,得到36个工况下A的值并代入式(13)中,计算得到对应的Δfi如表1所示。

表1 不同工况(nRi,TLi)时Δfi的取值Tab.1 The value of Δfiin different working conditions
将表1中离散的数据点绘制在三维坐标系中,如图6所示,通过曲面拟合的方法得到函数Δf=g(nR,TL)的表达式。

图6 Δfi与(nRi,TLi)在三维坐标系中的关系Fig.6 Relationship between Δfiand(nRi,TLi)in 3D coordinate system


采用最小二乘法拟合得到的曲面如图7所示,其中黑色实点表示离散数据点。计算此曲面对原始数据点的确定系数R和误差平方和SSE分别为0.992和1.42×10-4,这说明对原始数据拟合效果很好,且能对未知数据点的Δf进行预测。于是可根据式(16)计算任意转速nR和转矩TL条件下Δf的数值。

图7 最小二乘法拟合函数Δf=g(nR,TL)廹到的曲面Fig.7 Surface obtained by fitting Δf=g(nR,TL)with LSM
4)判断|ΔF(k)|> ΔUmin是否成立,若结果为“Y(是)”,说明fs尚未收敛至fm,则继续执行下一步进行判断;若结果为“N(否)”,说明算法已经收敛,返回步骤2)进入下一循环。
5)判断 ΔF(k)·Δfs(k)> 0 是否成立,若是,通过fs(k+1)=fs(k)-Δf对fs进行更新;若否,则通过fs(k+1)=fs(k)+Δf进行更新,最终返回步骤2)进入下一循环。
3 仿真结果
为验证所提出转速及效率优化控制方法的有效性,以Shinsei USR60超声电机作为控制对象并基于图1和图2建立系统仿真控制模型,Udc为12 V,变压器变比为1∶6,匹配电感取值Ls为2.4 mH,UF的采样周期Tsample为0.85 kHz,PI控制器参数KP,TI分别为0.1和0.9 ms。
3.1 电机转速及效率优化控制效果

图8 90 r/min,0.3 N·m时所提出方法的控制效果Fig.8 Control effect of the proposed method under 90 r/min,0.3 N·m
3.2 动态工况下不同效率优化算法控制效果对比
电机给定转速为70 r/min,转速环均采用PI控制器,效率优化算法分别采用分频段变步长和MEPT算法并在1.5 s时开始工作,负载转矩在3.5 s时由0.3 N·m减小为0.1 N·m,fs以及电机转速和工作效率如图9所示。

图9 动弦工况下不同效率优化算法控制效果对比Fig.9 Comparison of control effects of different efficiency optimization algorithms under dynamic conditions
从图9中可以看出,0~1.5 s内,两种控制效果没有明显差别;1.5~3.5 s内,分频段变步长算法优化速度较快,时间为0.395 s,转速波动为13.4%,但优化后效率仅为0.209,说明算法未收敛至最大效率点,收敛精度低。而MEPT算法优化时间为0.735 s,这对电机性能几乎没有影响,转速波动仅为1.6%,优化后效率达到了0.268;3.5 s之后,由于负载突变,分频段变步长算法出现振荡,导致转速波动很大,最大波动为19.5%,此时电机无法正常工作,而MEPT算法仅为6.4%,且最终稳定在70 r/min,电机近似达到最大效率0.194。
4 结论
针对超声电机效率过低的问题,通过分析电机驱动电路工作特性,确定fs和D1可以作为控制量,分别对转速和效率进行控制,并利用机械品质因数Qm的表达式对基于驱动电压有效值的效率反馈方式进行理论证明,然后针对电机的电压-效率-频率特性设计了最大效率点跟踪算法,采用基于最小二乘法的多项式曲面拟合方法计算频率更新步长。与现有效率优化方法相比,该方法不仅能够提高电机稳态时的工作效率,减小效率优化过程中的转速波动,同时还保证了动态工况下的稳定性。

