基于时域积分的变压器直流偏磁铁心振动信号特征提取

阳冠菲，罗 辉，邓华宇，闫 瑾，冯 健，罗日成

（1.长沙理工大学 电气与信息工程学院，长沙 410114；2.湖南涉外经济学院，长沙 410205）

0 引言

电力变压器作为电力系统中重要的变电设备，保障其正常运行对提高供电可靠性具有重要意义［1-2］。近些年来，随着特高压直流输电与城市轨道交通的发展，不少杂散直流电流通过星形联结绕组中性点流入变压器绕组，从而造成变压器的直流偏磁现象［3-8］。直流偏磁容易引起变压器内部铁心产生单边磁饱和，进而使励磁电流波形畸变，引起变压器过热［9］、系统无功波动［10］、继电保护误动［11］、异常振动与噪声［12］等问题，严重威胁电力变压器的安全运行。

国内外已有不少文献针对变压器直流偏磁问题进行了研究。文献［13-14］利用场路耦合法对换流变压器的振动与噪声进行了仿真分析，确定了变压器铁心在直流偏磁作用下的振动噪声水平，并综合分析了变压器电磁振动的影响因素。文献［15-16］研究了不同磁化方式下不同铁心区域的磁致伸缩特性，讨论直流偏磁磁场对铁轭以及芯柱磁致伸缩性能的影响。文献［17-18］分别对变压器绕组与铁心的振动进行了研究，得到了变压器偏磁绕组振动特征，并表明磁致伸缩是导致变压器铁心形变和振动加剧的关键因素。文献［19-20］研究了变压器直流偏磁前后的温升情况，得到了直流偏磁下变压器温度变化曲线。文献［21］通过振动测试数据，提出奇偶次谐波分量幅值之比的信号特征提取方法，并验证了提出的直流偏磁特征以及相应的特征提取方法的有效性，但该方法跟踪能力较差，容易受铁心磁过饱和干扰。

目前，对于电力变压器直流偏磁时频特征的研究，往往采用的是基于谐波复杂度来表征直流偏磁，但该方法有重要缺陷：容易受到铁心磁过饱和干扰。当变压器在过励磁情况下，振动信号的谐波量也会不断增加，因此有必要采用新的特征量来表征变压器直流偏磁程度。本文通过建立变压器三维有限元瞬态计算模型，比较分析了其过励磁与直流偏磁条件下不同监测点的振动信号，提出了用基于时域积分法的直流偏磁特征量λ表征直流偏磁严重程度的方法，可为直流偏磁监测与治理提供参考。

1 变压器直流偏磁铁心振动模型

1.1 铁心振动机制

铁磁材料具有磁致伸缩特性。在变化磁场作用下，铁磁材料的磁畴会产生旋转位移，宏观上表现为铁磁材料的尺寸变化，即产生了振动。铁心的磁致伸缩是磁场能与机械能相互转换的过程。直流偏磁造成变压器铁心单个电源周期内正负半周期磁通不对称，导致振动加剧。由于铁心磁通方向与铁心轴向的方向相同，铁心振动主要考虑轴向振动。铁心轴向振动加速度aZ可表示为：

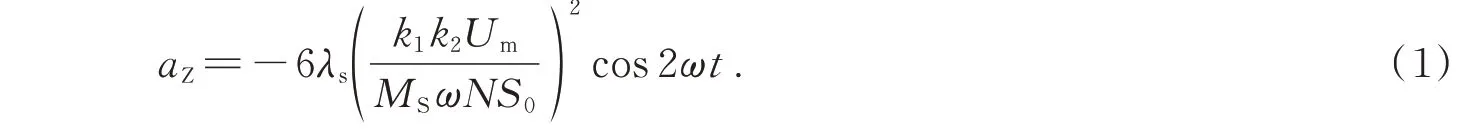
式中，λS为饱和磁致伸缩系数，Um为相电压幅值，MS为磁化强度，N为匝数，S0为铁心横截面积，k1、k2为拟合系数，ω为电源角频率。由式（1）可知，铁心振动基频为电源频率2 倍，即100 Hz。

1.2 模型物理场控制方程

仿真模型主要涉及电磁场与结构力场。电磁场主要涉及变压器绕组的电压电流、铁心中的磁通密度等物理量，结构力场主要涉及铁心磁致伸缩带来的振动。变压器结构力场计算的求解域方程为：

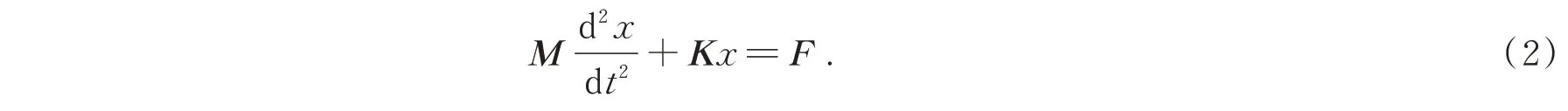
式中，M为质量矩阵，K为刚度矩阵，F为外力。

铁心伸缩效应可看作电磁能量和机械能量间的转换过程。铁心中的磁感应强度会同时增加材料的磁能与弹性势能，磁机耦合模型为：

式中，S为电磁刚度，K为机械刚度，A为磁场矢量，x为振动位移矩阵，J为外加电流密度，F为外部作用力，O和C为机械振动与磁场的双向耦合项。

变压器工作于工频电磁场中，根据麦克斯韦方程，变压器磁场对应的瞬态控制方程如下：

式中，A为磁场矢量，J为外加电流密度，μ为磁导率。

使用线圈特征建模高低压两侧绕组，利用场路耦合法将三维磁场有限元模型与电路微分方程相结合，场-路耦合模型中求解变压器绕组电压电流实时值的电路微分方程表达式为：

式中，LD为回路动态电感矩阵，R为回路电阻矩阵，u为瞬时电源电压。

1.3 模型参数设置

变压器在直流偏磁下的振动噪音分析涉及多个物理场之间的耦合，利用有限元软件COMSOL 对变压器建立三维瞬态模型，主要包括磁场、固体力学、电路及磁致伸缩等4 个模块。变压器直流偏磁仿真模型的等效电路如图1 所示。EA、EB、EC为变压器初级三相绕组的等效电源，幅值为变压器初级绕组相电压的 2倍。相电压的相位互差120°，R为输电线路与变压器绕组的等效电阻。RL为变压器次级绕组的负载。变压器的仿真参数设置见表1 所示。

图1 变压器直流偏磁仿真等效电路Fig.1 Equivalent circuit of transformer DC bias simulation

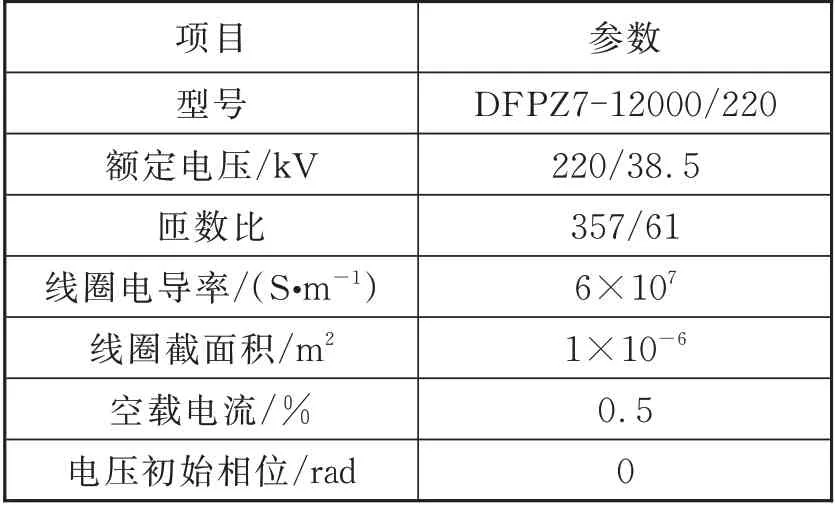
表1 变压器仿真参数Tab.1 Transformer simulation parameters

2 直流偏磁铁心振动的时域积分特征量

相同偏磁电流对不同型号变压器影响存在较大差异。为准确描述变压器直流偏磁程度，引入变压器直流偏置系数，定义为直流电流与额定空载电流峰值的比值，见式（6）。

式（6）中，Idc为直流电流，IN0为变压器额定空载电流峰值。

图2 为在未发生直流偏磁以及Kdc=1、Kdc=2 时的铁心表面位移大小变化曲线。从图2 可以看出，在直流偏磁影响下铁心在正负半周期内的振动位移大小并不对称，而是随着偏磁程度的增加，位移大小差异性逐渐扩大。这说明直流偏磁造成了铁心振动的正负半周期的能量差。时域积分特征量即利用该能量差来表征直流偏磁。

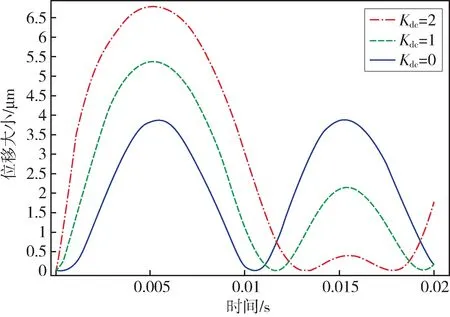
图2 直流偏磁下的铁心表面位移Fig.2 Surface displacement of iron core under DC bias

时域积分特征量是依据直流偏磁造成单个周期内正负半周期的振动信号能量差这一基本原理，对采集得到的变压器铁心振动信号的时域波形进行积分处理，采用振动信号波形与坐标轴形成的面积来描述振动信号在一个周期内的正负半周期的能量。时域积分特征量λ定义为：

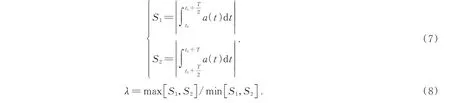
式中，T表示周期，a（t）表示振动加速度信号，t0表示周期内任意一时间点。由式（8）可知，λ为S1、S2两者中的较大值与较小值的比值，因此λ始终大于1。当振动信号正负半周期面积差越大，则振动能量差越大，λ值就越大，代表此时变压器偏磁越严重。

目前常用于量化描述变压器直流偏磁强度的指标是频谱复杂度，其表达式为：

式中，H代表频谱复杂度，Ri代表第i次谐波幅值，R1代表基波幅值。

频谱复杂度虽然在一定程度上能够描述变压器偏磁情况，但其无法排除变压器过励磁的干扰。当变压器在过励磁时，由于铁磁材料磁化曲线非线性的特征也会造成变压器振动谐波信号增加，而过励磁并不会造成振动能量差，因此时域积分特征量λ可有效避免过励磁的干扰，能更好地跟踪变压器直流偏磁程度。下文将通过仿真对时域积分特征量表征方法进行有效性验证。

3 仿真分析

3.1 监测点选取

为了选择合适的铁心振动信号监测点，需先对铁心整体振动情况进行分析。先选取Kdc=1 进行仿真，t=0.005 s 铁心振动位移正面图形（变量放大倍数为12 000）如图3 所示。从图3 可以看出，当Kdc=1 时，铁心产生了较大振动位移，最大位移量为0.25 μm，铁心位移主要集中于中心磁柱以及两侧铁轭内侧的转角处，且呈现上下对称的规律。图4 为Kdc=1 时铁心磁通密度分布图。从图4 可以看出，铁心中心磁柱以及两侧铁轭内侧转角处的磁通密度较大，最大磁通密度达到1.85 T，而外侧转角处的磁通密度较小，在0.6 T～0.8 T 范围内。从图3、图4 可以发现，磁通密度较大的地方振动位移也比较大。

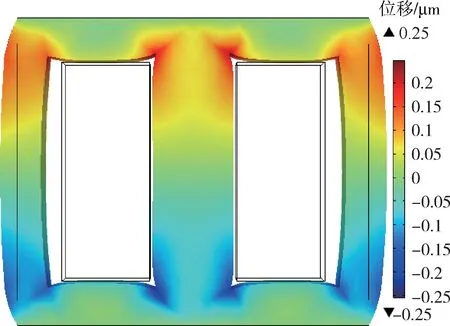
图3 铁心振动位移Fig.3 Iron core vibration displacement

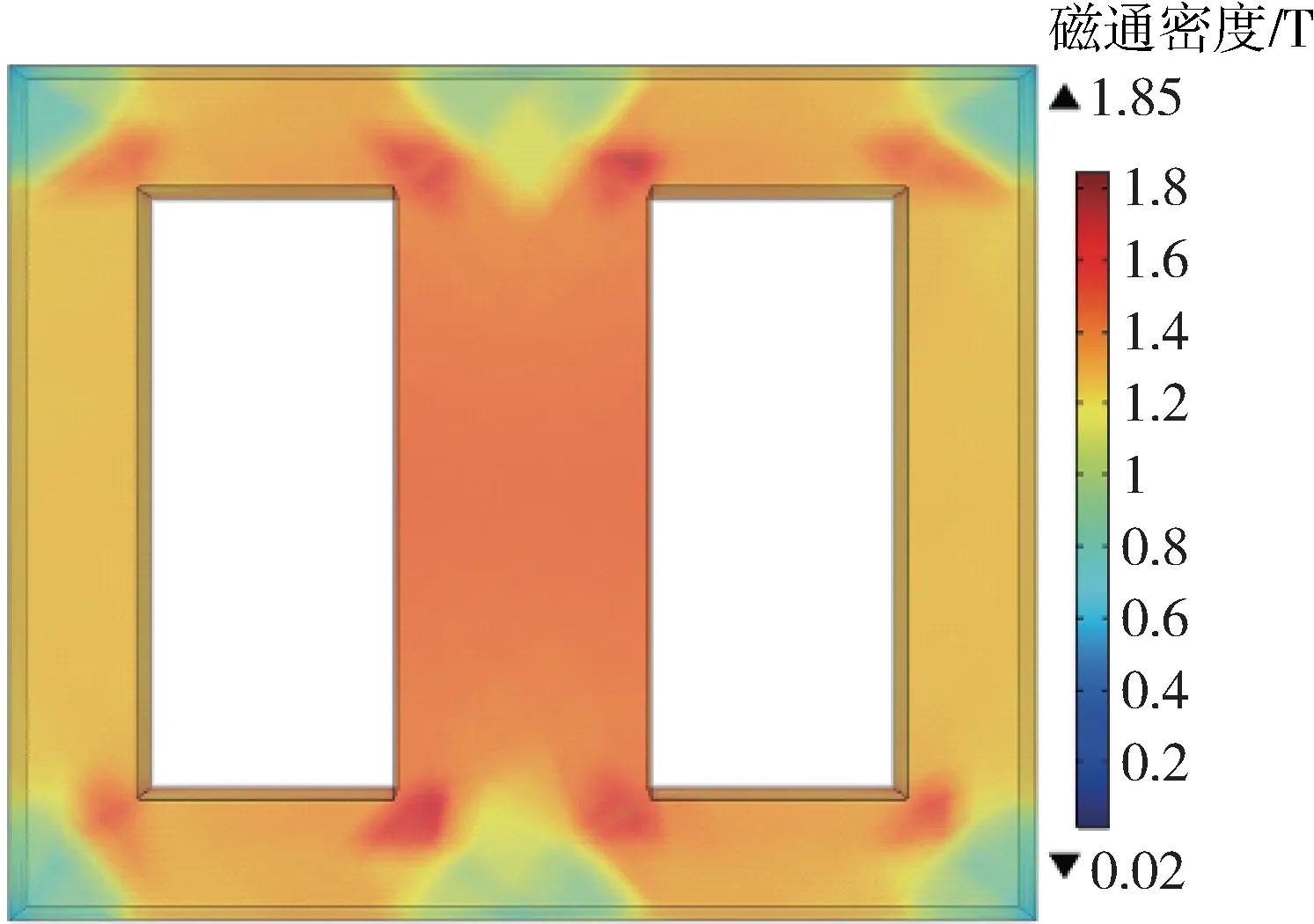
图4 铁心磁通密度分布Fig.4 Distribution of magnetic flux density

参考磁通密度与位移形变仿真结果，为了能更好地分析变压器直流偏磁振动特性，综合考量后确定了A（-850 mm，2 750 mm）、B（-3 250 mm，1 560 mm）、C（-850 mm，1 560 mm）3 个信号监测点。A点反映了铁心转角处的振动情况，B、C两点反映了中心磁柱及铁轭表面的振动情况。监测点布置情况如图5 所示。

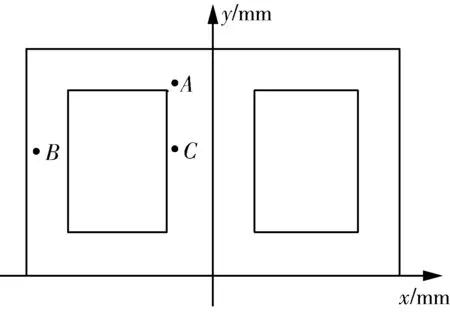
图5 信号监测点布置Fig.5 Arrangement of signal monitoring points

3.2 变压器直流偏磁振动分析

为比较变压器在正常状态时、直流偏磁时、过励磁时的变压器铁心振动信号，选取Kdc=0 和Kdc=1 两种状态，变压器高压侧施加额定电压UN，仿真得到变压器3 个信号监测点A、B、C的轴向振动加速度时域波形如图6、图7 所示。在高压侧施加1.05UN，仿真得到变压器在过励磁状态下的振动信号如图8 所示。从图中可以看出，在没有直流偏磁情况以及过励磁情况下，铁心振动信号波形的正负半周期均基本呈现对称特征；3个信号监测点的振动强度大小比较为A＞B＞C，振动加速度幅值大致为0.25 m/s2、0.05 m/s2、0.017 m/s2；在变压器过励磁时，3 个点振动强度比较结果为A＞B＞C，振动加速度幅值大致为0.281 m/s2、0.059 m/s2、0.025 m/s2。

图6 无偏磁电流振动信号波形Fig.6 Vibration signal waveform without bias current

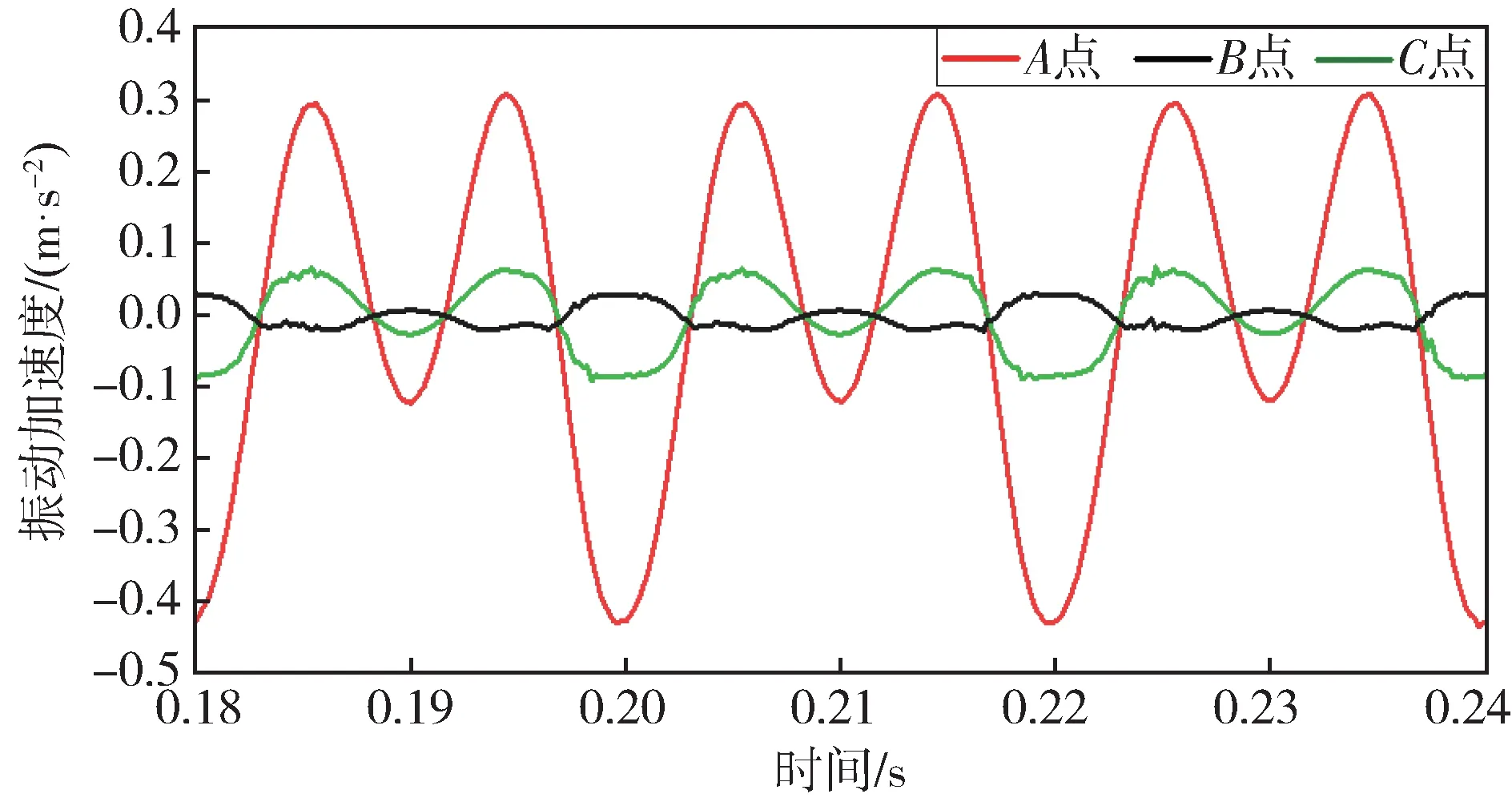
图7 有偏磁电流振动信号波形Fig.7 Vibration signal waveform with bias current

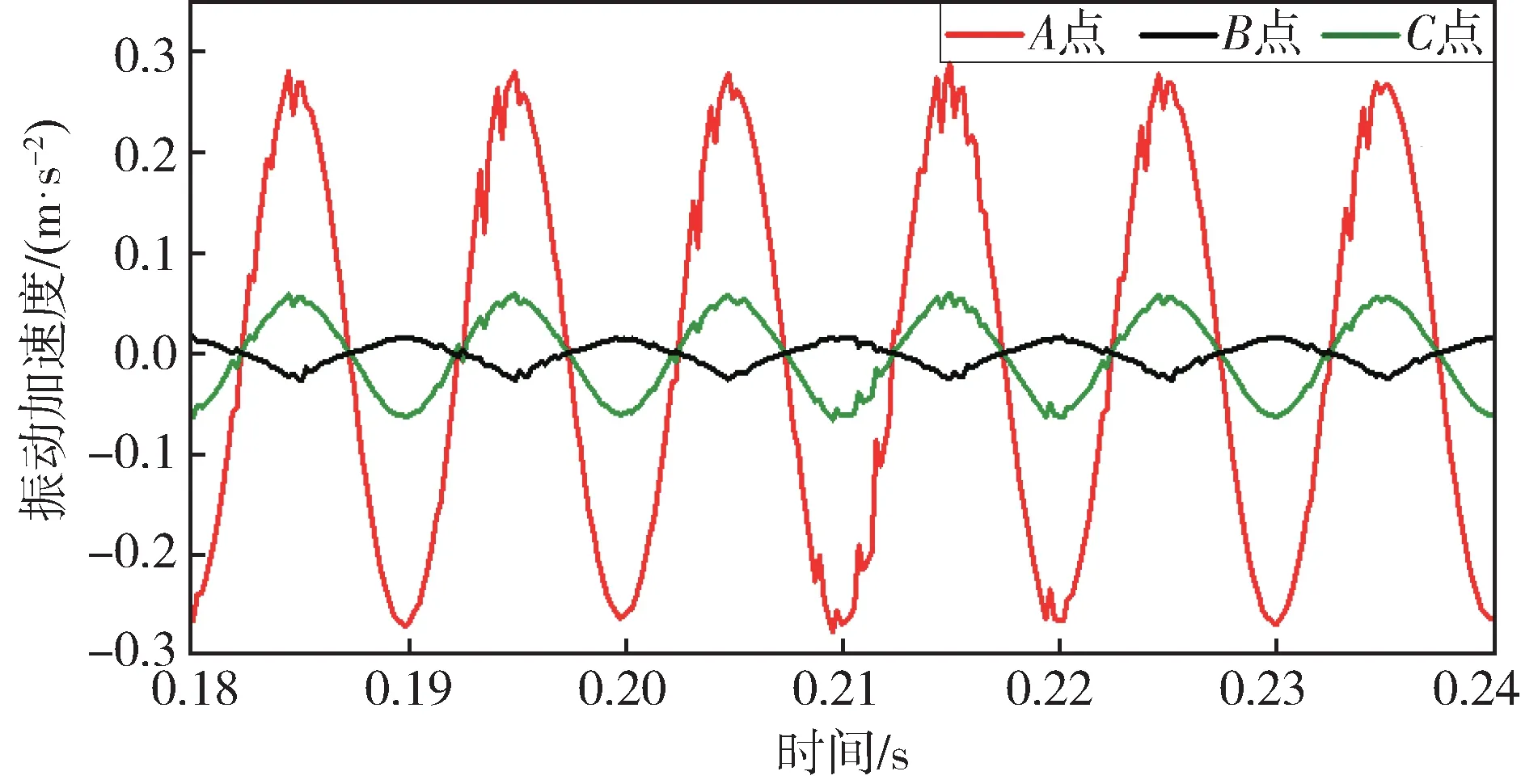
图8 过励磁振动信号波形Fig.8 Vibration signal waveform with over excitation

当偏磁系数Kdc=1时，铁心振动信号波形发生明显畸变，且波形的正负半周期明显不对称，致使变压器正负半周期能量存在较大差值。当偏磁系数Kdc=1 时A点振动加速度的正、负半周期幅值分别为0.298 m/s2、-0.435 m/s2，负半周期比正半周期幅值增大了46%。

3.3 频谱复杂度计算

对采集的变压器振动信号进行傅里叶变换得到图9—图11 的振动信号频谱。由图可知，变压器振动加速度信号成分以50 Hz、100 Hz 频率为主。偏磁电流使变压器振动频谱复杂度增加，增加较为明显分量主要包括直流分量、150 Hz 的三次谐波分量。

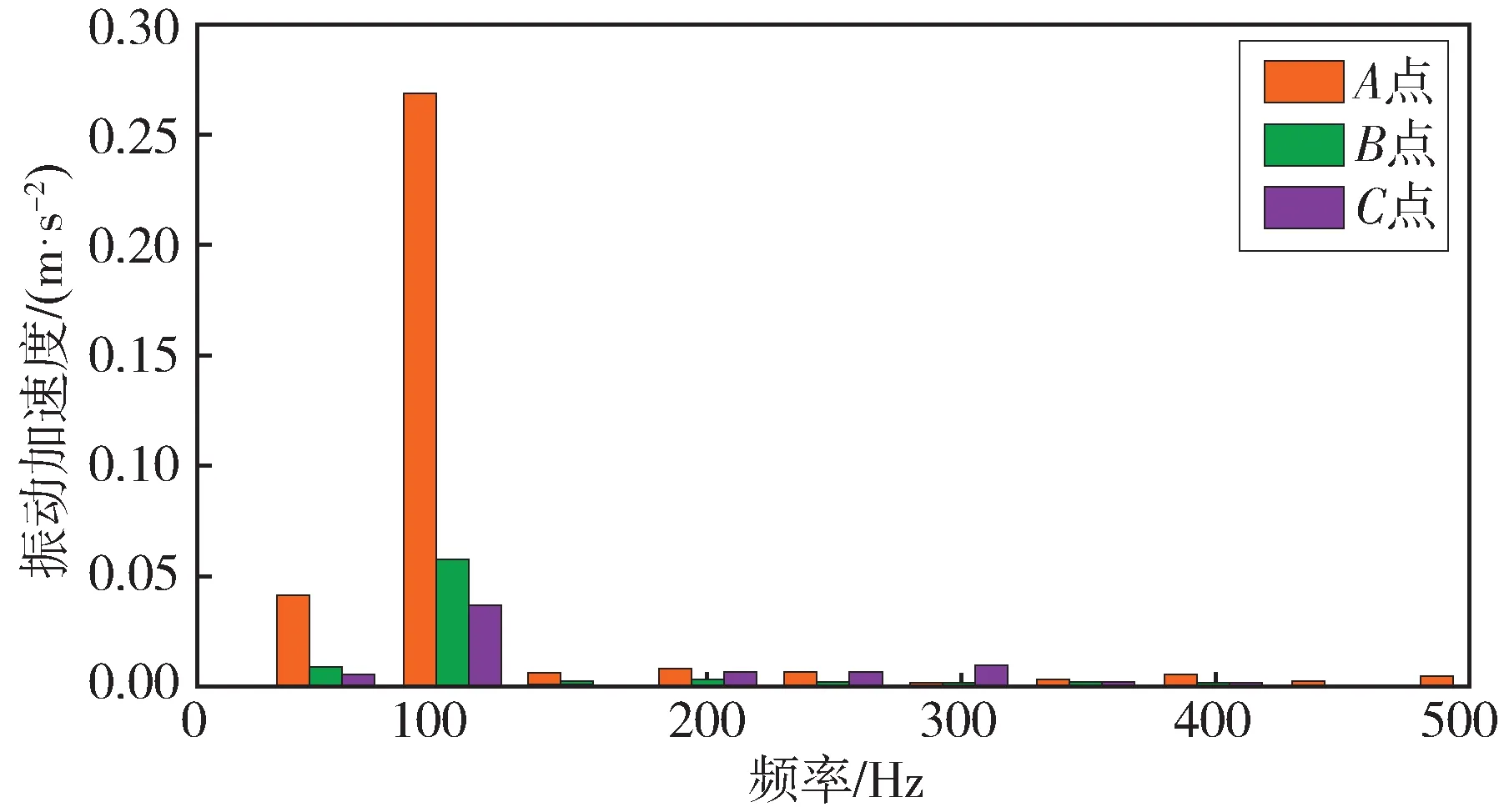
图9 无偏磁电流振动信号频谱Fig.9 Vibration signal spectrum without bias current

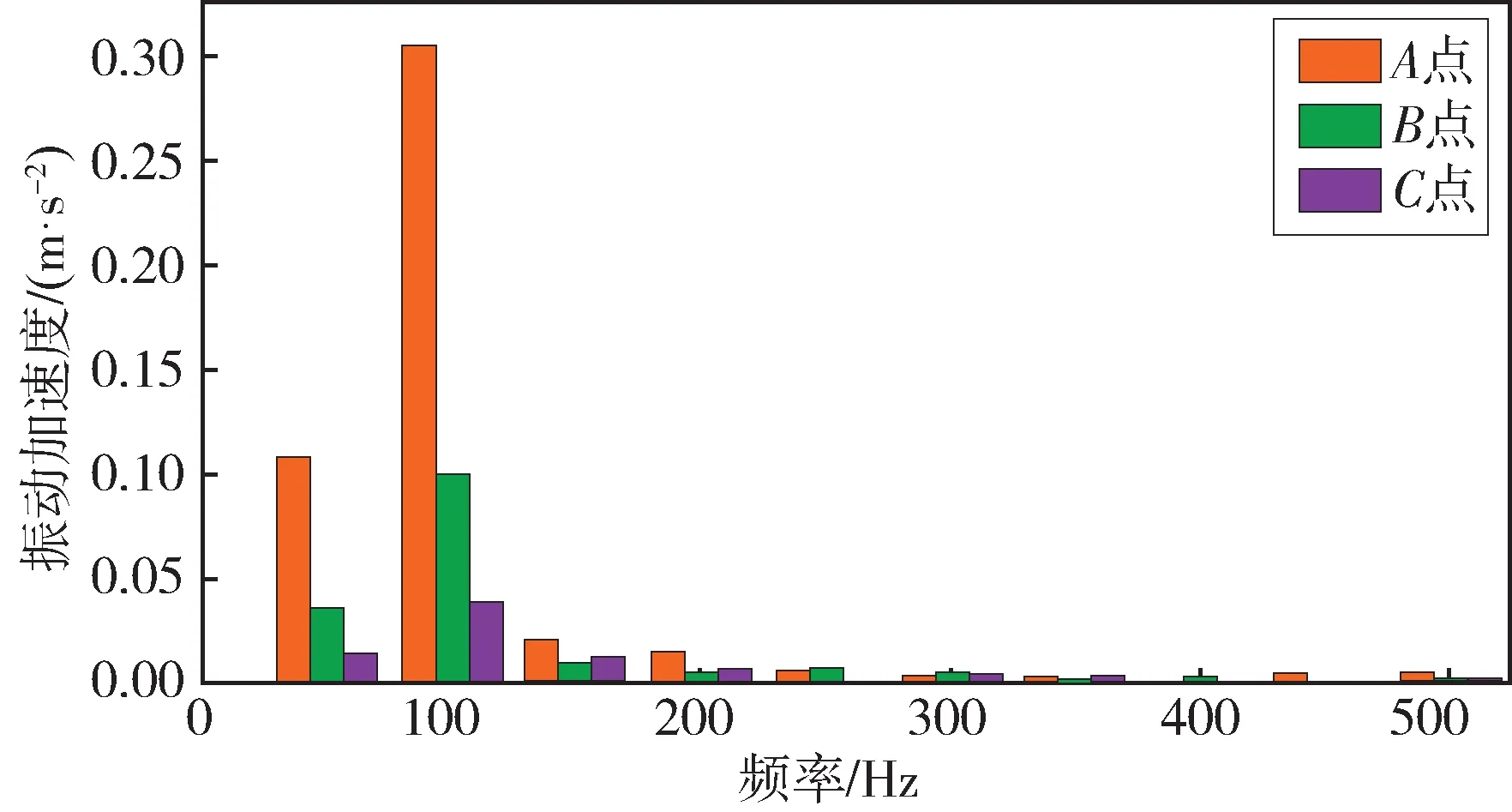
图10 有偏磁电流振动信号频谱Fig.10 Vibration signal spectrum with bias current

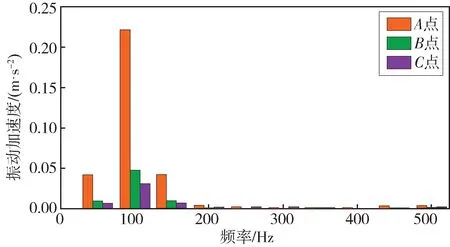
图11 过励磁电流振动信号频谱Fig.11 Vibration signal spectrum with over excitation

通过三种运行状态下的频谱图，可以得到各监测点在各频段的幅值大小。根据频谱复杂度计算方法，得到变压器在Kdc=0、Kdc=1 以及过励磁状态下的频谱复杂度计算结果，如表2 所示。

从表2 看出，在Kdc=0，铁心振动信号的频谱复杂度最高为C点处，大小为23.88%。当发生直流偏磁Kdc=1 时，频谱复杂度大大增加，最高为39.31%，与同一监测点未发生直流偏磁相比增加了约64.61%。当变压器处于过励磁状态时，频谱复杂度相较无偏磁电流时也会增加，说明此时变压器中性点虽然没有流入直流电流，但由于铁心非线性磁化特性，振动信号频谱复杂度也增加了不少，此时通过频谱复杂度来判断变压器的偏磁状态会受到干扰。

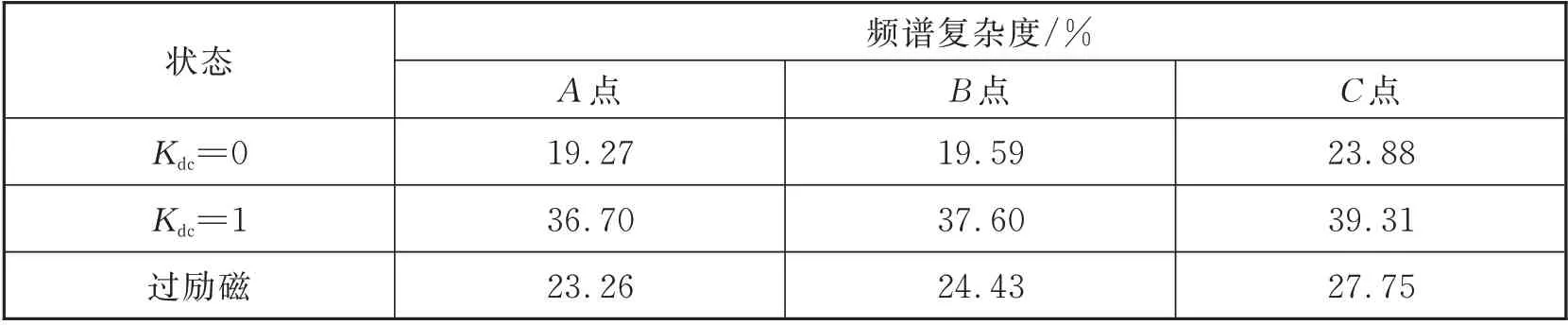
表2 频谱复杂度计算结果Tab.2 Spectrum complexity calculation result

综合振动信号时域波形与频谱图分析，直流偏磁使振动信号产生了波形畸变，正负半周波形幅值存在较大差异。变压器在过励磁时振动谐波也会增加，因此基于频谱复杂度的特征提取方法具有较大局限性。下面将对不同直流偏磁系数下的时域积分特征量λ进行计算，以验证该方法可良好表征变压器偏磁程度。另外，对变压器在不同励磁电流的特征量λ进行计算，以验证该方法可排除变压器过励磁干扰。

3.4 特征量计算

为验证时域积分法特征量λ能很好地表征变压器偏磁程度，文中将仿真波形导入数据分析软件，通过积分运算，计算了不同直流偏磁系数下的特征量λ值，计算结果如表3 所示。从计算结果可以看出，当变压器未发生直流偏磁时，各点的直流偏磁特征量λ均大于1，这与时域积分法分析相一致。随直流偏置系数Kdc增加，特征量λ逐渐增加，存在较为明显的单调递增规律。

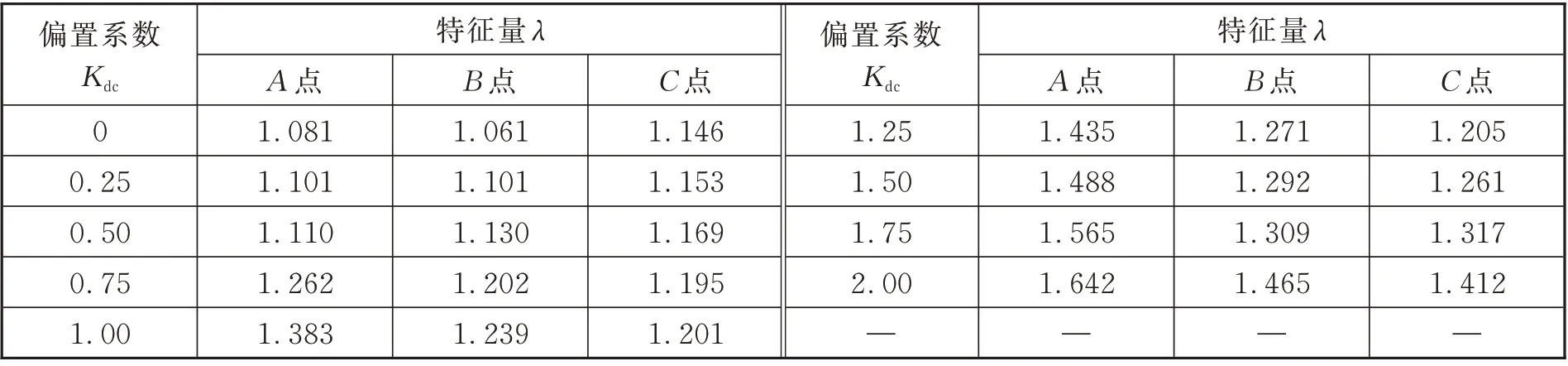
表3 不同直流偏磁系数下特征量Tab.3 Characteristic quantity under different DC bias coefficient

为验证特征量λ可排除变压器过励磁干扰，考虑到实际变压器电压调整率波动范围一般在5%以内［22］，假设变压器过励磁保护不动作，分别计算U1=UN、U1=1.01UN、U1=1.02UN、U1=1.03UN、U1=1.04UN、U1=1.05UN，Kdc=0 时6 组状态下的特征量λ，不同励磁电压下特征量计算结果如表4 所示。从计算结果可以看出，当变压器高压侧励磁电压逐渐增加时，特征量λ并不会随着其逐渐增加，说明该特征量可以较好地排除变压器过励磁的干扰，仅仅只反映变压器偏磁的程度。

表4 不同励磁电压下特征量Tab.4 Characteristic quantity under different excitation voltage

为了更加直观地分析特征量λ的变化规律，将直流偏磁特征量除以Kdc=0 时的特征量λ，即8 组特征量λ计算结果与Kdc=0 时的特征量λ取比值，得到标幺化的特征量λ。标幺化λ随直流偏置系数Kdc变化曲线如图12 所示。计算结果显示，铁心的各信号监测点的特征量标幺化数值均随直流偏置系数增大而增大。当Kdc=2 时，A点的标幺化特征量λ为未发生直流偏磁时（Kdc=0）的1.5 倍。将过励磁状态下的特征量λ除以U1=UN时的特征量λ，即5 组特征量λ计算结果与U1=UN时的特征量λ取比值，得到标幺化的λ计算结果。标幺化λ随励磁电压标幺值变化曲线如图13 所示。

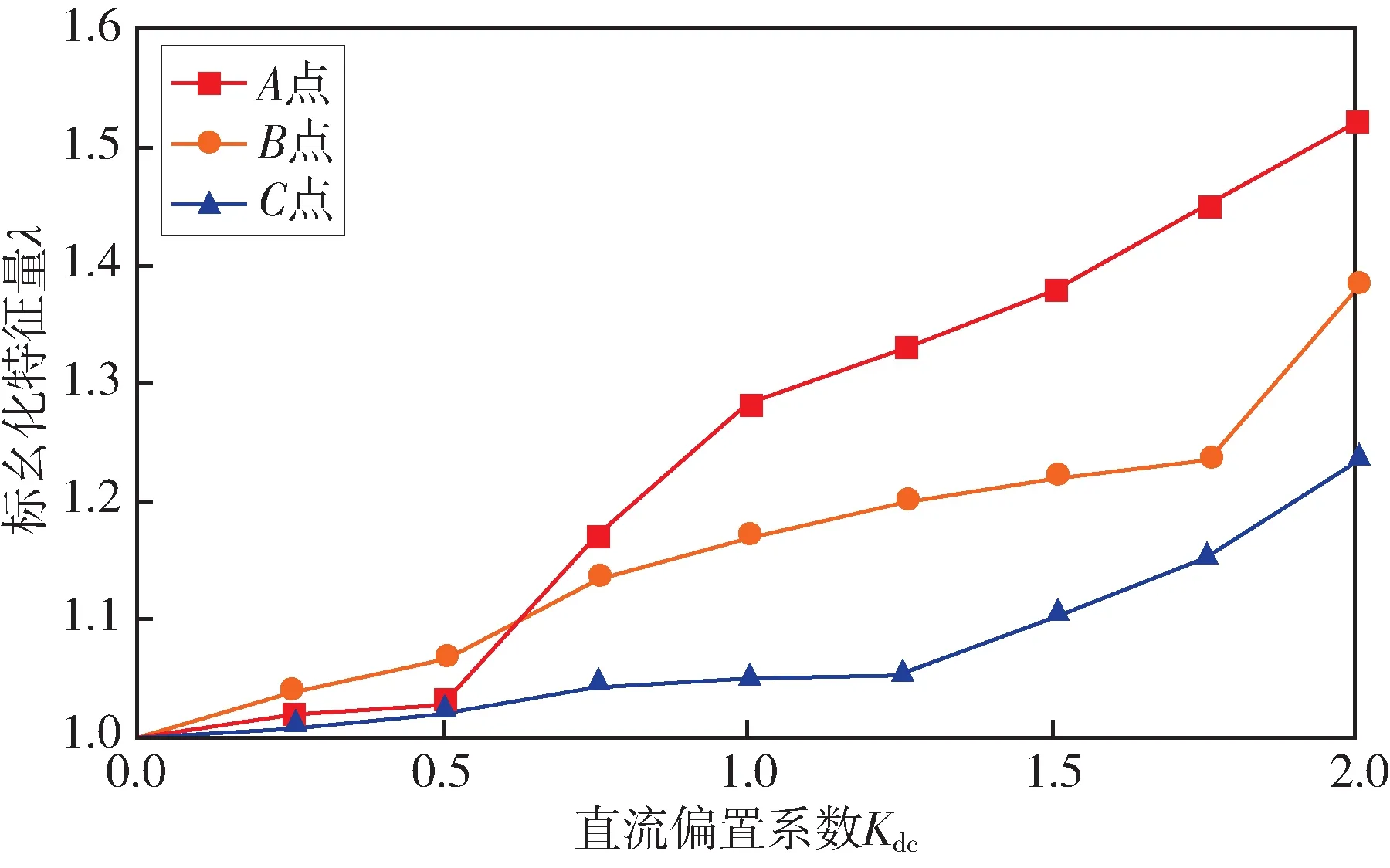
图12 特征量随直流偏置系数变化Fig.12 Characteristic quantity changes with DC bias coefficient

图13 特征量随励磁电压变化Fig.13 Characteristic quantity changes with excitation voltage

当变压器未发生直流偏磁而处于磁过饱和状态时，随着励磁电压逐渐增加，铁心的各信号监测点的特征量标幺化数值只发生了微小波动，波动范围约在（0.99，1.01）区间，说明磁过饱和对特征量λ几乎没有任何影响。综上分析，通过计算振动信号的时域积分特征量λ可以有效提取变压器直流偏磁特征，从而反映变压器直流偏磁严重程度。该方法相较基于频谱复杂度方法而言，具有较强的抗磁路饱和干扰的优点。

4 总结

本文提出了一种新的基于时域积分的变压器直流偏磁振动信号的表征方法。该方法利用直流偏磁造成的单个周期内正负半周期的振动信号能量差，对变压器振动信号的时域波形正负半周期进行时域积分，提取变压器直流偏磁特征量λ。经过仿真验证，特征量大小可随变压器直流偏磁程度加深而逐渐增大，可用于直流偏磁的检测与诊断。与频谱复杂度指标相比，本文所提方法具有实用性强、准确性高、跟踪性能好等优点，可以避免变压器过励磁的干扰。