大数据技术在电力故障预测方法中的研究

杨健， 叶秋红， 王怀俊， 马德萍

(国网宁夏电力有限公司吴忠供电公司， 宁夏，吴忠 751100)

0 引言

随着经济的发展，大数据技术得到了快速的推广和普及，大数据技术在电力故障预测中有着普遍的应用。李俊艳[1]针对大数据分析角度提出数据三角模糊函数的方法，采用主客观相结合的方法分析电力故障发生的概率。袁智勇等[2]利用评价分析法对电力故障情况进行评价，分析电力故障发生的概率。陈清明等[3]提出FFTA分析方法，即利用模糊故障树的思路将事件发生的概率用梯形模糊数替代，深入分析电力故障情况。罗兰溪[4]利用Apriori算法，分析电力故障的关联关系，以及发生故障的关联原因，分析电力故障影响因素的关联性。有学者利用FDS和梯形模糊事故树结合建立电力故障预测模型，分析多种有效影响因素，以此判定电力故障的发生程度[5-6]。

综上所述，目前专家学者的研究主要是利用大数据手段中的梯形模糊事故树进行预测，但是并未对梯形模糊事故树存在的线性处理方法缺陷进行改进，导致预测的准确度仍有待提升。因此，本文从改进梯形模糊事故树的角度出发，建立基于大数据技术的电力故障预测模型，提高对电力故障预测的精度，降低预测误差。

1 梯形模糊事故树在大数据中的应用

梯形模糊事故树是大数据技术中对电力系统故障处理的常用方法，旨在利用构建事故树的方法，在梯形模糊事故树上表示故障事件发生的概率[7]。将事故树与离散小波分解相结合，不仅可以分析电力系统的故障，还可以从电力信号的角度进行分析。

为了保证采集信号的连续性，在噪声信号、有用电流信号之间分别设置平滑过渡区。这种情况下，离散小波分解函数可以表示为

δ(h)=h+Y2l+1-Yh≥Y

1(2l+1)Y2lh2l+1h≤Y

(1)

式中，h表示电流信号，δ表示降噪处理后离散小波系数，l表示小波系数序列，Y表示最优噪声处理阈值。按照最大、最小估计方法进行计算，得到噪声阈值为

Y=φ2lnF

(2)

式中，φ表示噪声标准差，F表示故障检测过程中采样点数量，ln表示对数函数。利用式(2)计算的阈值对采集的电力信号进行降噪。

2 改进的梯形模糊事故树的电力故障预测模型

采用以矩阵分解理论为核心的奇异值分解技术，对电流信号进行变换处理。当某一个矩阵内包含的行向量、列向量之间存在线性关系，则向该矩阵的两侧分别乘一个正交矩阵，形成对角阵，则该对角阵的对角线元素就是奇异值分解结果如下:

ηYQM=P

(3)

式中，Q表示故障检测领域上的p*q阶矩阵，η、M表示正交矩阵，P表示矩阵的奇异值分解。

其中：

η=f1,f2,…,fε

M=v1,v2,…,ve

(4)

P=κ10…0

0κ2…0

00⋱0

000κσ

(5)

并且：

σ=min(p,q)

(6)

式中，f表示正交矩阵η内的特征向量，ε表示正交矩阵η内向量总数，v表示正交矩阵M内包含的特征向量，e表示矩阵内向量总数，κ表示奇异值，σ表示分解后形成的奇异值总数量，min表示最小化函数。

当电力系统出现故障后，电流和电压的波形都会出现较大变化，针对一系列电流离散信号构建特征矩阵，以此作为奇异值分解特征提取方法的基础。通常情况下，为了保证奇异值分解结果能够更好地反映出数字化三维电力故障信息，将离散序列的右移步长设置为1，其生成的特征矩阵属于二维空间，该特征矩阵可以用公式表示为

T=t1t2…tτ

t2t3…tτ+1

⋮⋮⋱⋮

tφtφ+1…tφ+τ-1

(7)

式中，T表示故障电流信号离散序列，t表示故障信号，τ表示行向量，φ表示空间维度。利用式(7)得到一个待分解的特征矩阵，针对该矩阵进行奇异值分解，分解结果可以更加准确地提取出故障特征。

3 实例分析

在电力系统故障检测中，以某检测区域为例，采集该区域变电设备电流的实时信息，采用db5小波基函数，进行小波变换处理，得到多个电流信号近似波形、细节波形，形成图1所示的小波分解图。

图1 小波分解图

在图示中，d1、d2、d3、d4和d5表示了不同层小波分解结果。根据小波分解图可以看出，数字化三维变电站出现故障问题后，原始电流信号内包含的高频分量波形出现较大变化，表明故障时刻信号局部特征的改变。为了加强故障检测的准确性，本次采集了三相电流信号，运用文中提出的改进的梯形模糊事故树，即奇异值分解方法提取出原始电流信号内包含的特征信息，并定义信号特征参数,再结合小波变换算法、奇异值分解原理计算变电站运行过程中该区域最大小波奇异值，当最大小波奇异值出现大幅度突变趋势，表明此时出现了故障问题。结合三相电流信号的波形特点，将最大小波奇异值计算的时间窗口长度设置为15 ms。

为了加强故障检测结果的准确性，本次实验采用小波变换算法，对图1内显示的d5层小波分解结果进行相空间重构，形成与原始电流信号相符的特征矩阵。控制时间窗口不断向右侧移动，获取最大小波奇异值仿真波形图，如图2所示。

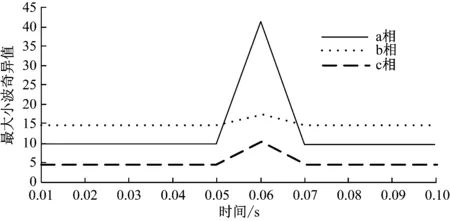
图2 故障发生时各相最大小波奇异值波形图

本次实验测试过程中，同时采用CFS、PSO-RF方法进行故障检测作为对比实验(见图3)。为了验证文中提出检测方法的抗干扰性能，在实验过程中，不断向信号中添加噪声信息，对比3种方法的故障检测误差变化情况，体现文中设计方法的优越性。

由实验结果可知，文中设计故障检测方法的误差不再稳定在0.04，而是呈现出上升趋势,而基于CFS的故障检测方法，在干扰噪声为10 dB时就出现了误差增长情况，当干扰噪声为32 dB时，故障检测误差达到了0.47。与上述两种检测方法相比，PSO-RF方法的抗干扰性能更差，当干扰噪声为2.4 dB时,检测误差无法保持稳定。综上所述，文中提出的电力系统故障检测方法抗干扰能力与其他两种方法相比，提升了45%、66%。

图3 3种故障检测方法的抗干扰性能对比图

4 总结

(1) 改进的梯形事故树预测模型可以较大程度地降低预测误差，与其他方法相比，误差分别实现了一定程度的减弱。

(2) 本研究提出的电力系统故障检测方法具有较强的抗干扰能力，可以在多种干扰因素下保证故障检测的准确性。