开磁路工字形电感的磁场分析及电感计算方法研究
黄家毅
(东莞铭普光磁股份有限公司,广东 东莞 523000)
0 引 言
电感器作为三大被动元器件,被广泛使用在各种电子电路或者设备中,具有在磁场中存储和转换能量的功能。功率电感作为常见电感类型,通过电磁转换实现能量传递以及电路中电压转换功能。常用的直流转换器拓扑类型包括降压、升压、升/降压,单端初级电感转换器等。在直流转换器中,直流分量大,要求电感器抗直流偏置能力强。众所周知,增加气隙长度可以提升抗饱和能力,对于开磁路的工字形,因低成本、高饱和特点,被广泛应用在直流转换模块中。电感值L主要作用在直流电路来控制工作模式和电流纹波率大小。作为第一个关键设计参数电感值,在公开文献中给出了R棒电感和空心螺旋弹簧式线圈的电感计算方法,至于开磁路工字形的电感或电感系数,磁材或电感行业内都是依靠实测得到[1,2]。虽然通过电磁仿真技术也可获得电感值,但前提需要购买昂贵的软件和拥有经验丰富的仿真工程师。本文对工字形磁场和磁路模型分析,基于磁阻理论方法通过简化磁路模型得到一种简单易用的工程计算方法。通过实验测量和理论计算进行对比验证,误差较小符合工程设计需求,从而极大缩短开发周期。
1 电感计算推导过程和计算方法
1.1 带气隙电感磁路模型及电感计算
磁阻是磁路中对磁通量流动的阻力,它对磁通量流动的阻力与电阻对电流在电路中流动的阻力相同。 铁氧体铁芯材料的磁阻Rc为:

式中:μ0为真空磁导率,取4π×10-7;N为线圈圈数;μr为磁体的有效磁导率;Ac为磁体有效截面积,m2;lc为有效磁路长度,m。
根据上面定义可得气隙的磁阻Rg为:

式中:μg为空气相对磁导率,其值为1;Ag为磁体有效截面积,m2;lg为间隙长度,m。
带气隙电感磁路模型如图1所示,对于图1(a)中含有N匝线圈的铁氧体电感[4],有气隙电感的安培定律为:

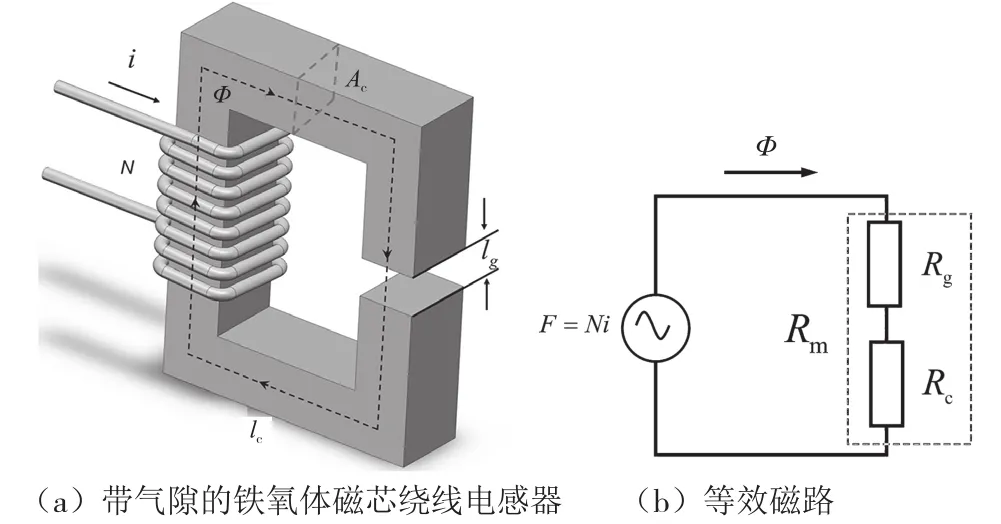
图1 带气隙电感磁路模型
当加载交流电i时,N匝绕线电感产生磁动势F,其磁路等式为:
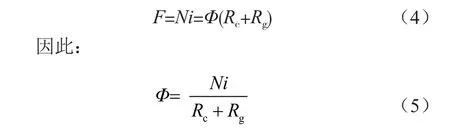
根据法拉第感应定律,对线圈施加交流电流i时,产生的电压u为:

由式(6)中得到带有气隙的铁氧体铁芯电感器的其电感L为:
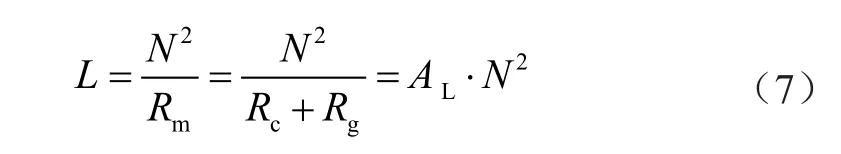
式中:Rm为磁路中的总磁阻;AL为电感系数。
1.2 工字形电感磁路和磁场分析
对于工字形这种开磁路,空气部分扩散磁通分布及其不均,工字形绕线电感磁通密度仿真如图2所示。空气中磁通面积和长度无法通过一般测量仪器获得,而且还会随着磁体本身形状和绕线槽的长度变化而变化,因此很难计算空气磁阻。开磁路的工字形电感器总磁阻Rm的等效电路如图1(b)所示,是磁芯磁阻Rc和空气磁阻Rg之和。因此,为了获得较为精确的电感,磁芯和空气的磁阻都需要准确计算。

图2 工字形绕线电感磁通密度分布
1.2.1 磁芯磁阻计算
闭合磁路磁芯有效磁路参数可以按照IEC 60205标准来计算从而得到磁阻,但没提及这种工字形开磁路的磁芯计算方法。工字形磁体从形状上就是把罐型POT外围环形实体部分切除,参考罐型磁芯磁路有效参数计算方法,调整后得到适用于工字形,其磁路及其结构见图3,有效参数的计算则如表1所示[5]。如果磁芯设计满足磁路面积处处相等的理想前提下,其有效参数可采用简易计算方法:Ac为中柱面积(S=πd2/4),磁路长度lc为各段分段长度之和(lc=∑ li, i=1,2,…,5)。

表1 工字形磁芯有效磁路参数计算等式

图3 工字形磁芯磁路结构示意图
1.2.2 扩散磁通的分析及其磁阻的计算
对于工字形开磁路,空气部分扩散磁通的磁路长度都很大,空气部分磁阻远远大于磁芯的,一般有数十到数百倍的差距,所以空气中扩散磁通磁阻计算精度很大程度决定了电感计算精度。如何对空气扩散磁通分布的模型进行“可视化、可测量”描述则是此部分磁阻计算的关键。
从图2工字形绕线电感磁通分布仿真图可知,空气中的扩散磁通不是均匀分布的,在外部空气中磁通密度分成两部分,其数值分别0.001 2 T和0.000 6 T 。靠近绕组A区域磁力线主要是从工字形上叶片边缘溢出进入空气中然后返回下叶片边缘。A区域的磁力线密度远大于外围B区域,B区域显示为0.000 6 T,这部分磁通从磁芯顶和底部泄漏出来。在绕线槽里面,由于线圈导体材质为铜,铜具有抗磁性,那么理论上穿过绕组磁力线很少,而且在图2中的仿真数值也证明了这一点,因此可忽略。磁力线总是力图缩短磁通路径或者沿着导磁能力大的物质或地方流动以便减小磁通流动阻碍,这种现象称为“磁阻最小原理”[6]。因此,远离磁体的磁力线肯定会越来越稀疏。由于A区域磁力线数量远远大于B区域,那么这两部分磁通的磁路长度均值肯定略大于A区域长度均值。忽略工字形上下部分溢出磁力线的长度,对磁路长度均值影响也不大,也就相当于磁通从上下叶片边缘溢出。如上所述,简化后得到如图4所示的工字形绕线电感空气扩散磁通分布示意图。对于图4(b)中绕组完全布满绕线槽情况,忽略穿过绕组部分磁通,磁力线都分布在磁芯外部空气。而在没有绕满的情况下,除了磁芯外部,磁芯内部磁通直线穿过没有绕组的空间,如图4 (a)所示。
图4(a)为绕组没绕满外部空气磁通的分布示意图,此刻扩散磁通的磁阻Rg则是由磁体内部空气磁阻Rig和磁体外部磁阻Rog并联组成,则等式如下:

图4 工字形绕线电感空气扩散磁通简化模型示意图

内部空气磁阻Rig为:

式中:lg(lg=l1)为内部空气扩散磁通的磁路长度;Aig为内部扩散磁通的面积。
内部扩散磁通的Aig为:
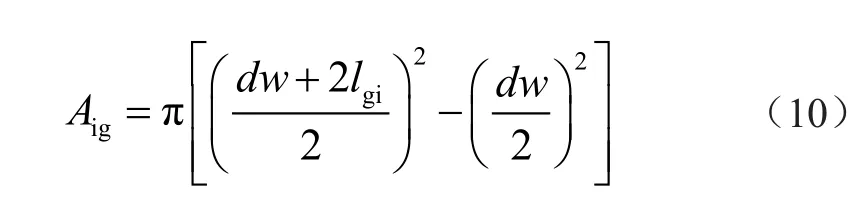
式中:dw(d<dw<D)为绕组外围直径大小;lgi内部扩散磁通宽度。
外部空气磁阻Rog为:

式中:Aog为外部扩散磁通的面积;log为外部空气扩散磁通的磁路长度。
外部扩散磁通面积Aog为:

假设空气这部分磁路分布在相对磁导率为1的磁体里,其外部扩散磁通的磁路长度按照IEC 标准方式描述成两部分弧长加上lg,其等式如下:
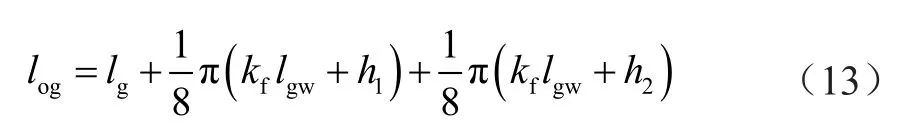
假设这两部分A和B扩散磁通密度相同,外部扩散系数kf为0.5,磁力线密度差别比较大,靠近磁体的磁力线数量多,远离磁力线的数量少,那么可得0<kf<0.5。
假设外部扩散磁通密度处处相等,并把外部扩散磁通均分为n份,其总磁阻相当于n个并联,则有:

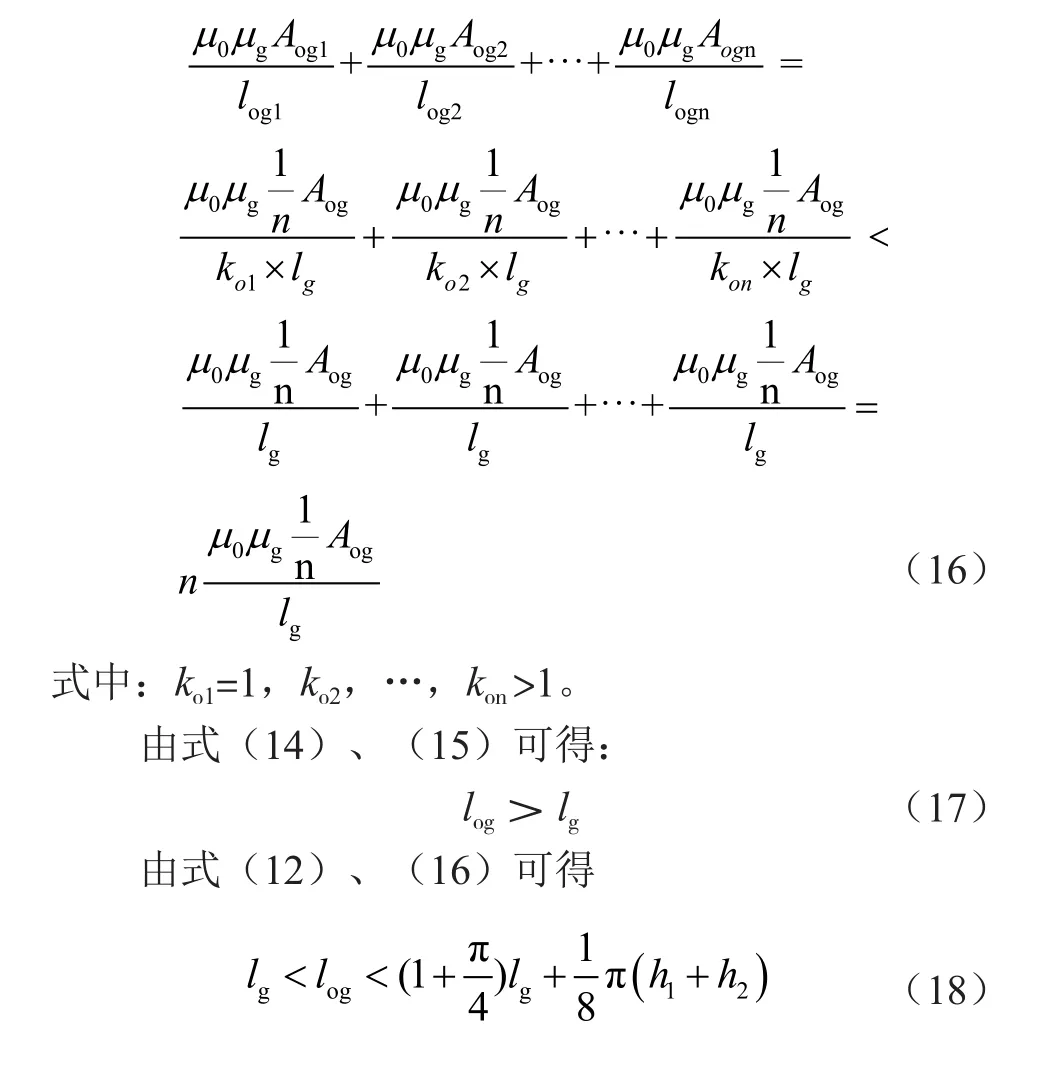
式(17)数值范围还是很大,为了进一步简化,应用磁阻最小原理,磁力走直线道,就相当于磁力线走的路径直上直下。假设磁力线均匀分布,外部扩散磁路长度最大值可以认为绕线槽幅宽lg加1/2上下叶片的厚度,按照图4(a)扩散磁通简化模型,磁力线密度分布不均时,大部分磁力线集中在叶片厚度的1/3,那么可得到:

结合磁芯制造商工字形磁芯尺寸数据表和式(17)、式(18)计算得到:

式中:k0为外部扩散磁通长度倍增系数,非恒定值,和磁芯和绕组结构相关,推荐值为1.1。
空气扩散磁通宽度lgw为:

式中:k1为扩散系数,非恒定值,是工字形线槽幅宽l1,磁芯叶片形状和尺寸、线圈位置、绕组结构相关因素的综合函数。当气隙lg很小时,文献资料中提及扩散磁通宽度lgw为气隙lg的1.0~1.2倍,随着lg的增加,根据磁阻最小原理,等效扩散宽度lgw会变小,根据电磁仿真磁通密度分布图模拟结果可知,k0,k1和lg之间关系以及相关为推荐值如表2所示[7]。
2 实验结果与讨论
基于磁阻以及结合简化工字形电感的磁通模型的方法推导出电感值的计算等式,然后使用多种材质、多种不同尺寸工字形磁芯绕制而成电感进行测试验证。每组(序号)测量10个样本的尺寸和电感值(100 kHz测试频率)并取其对应平均值,尺寸测量值和磁阻相关计算列于表3和表4中,然后采用式 (7)~式(12)、式(20)、式(21)以及表2中k0,k1推荐值来计算电感值,其电感计算值和实测值如表5所示。

表2 气隙lg与k0、k1推荐数值关系表
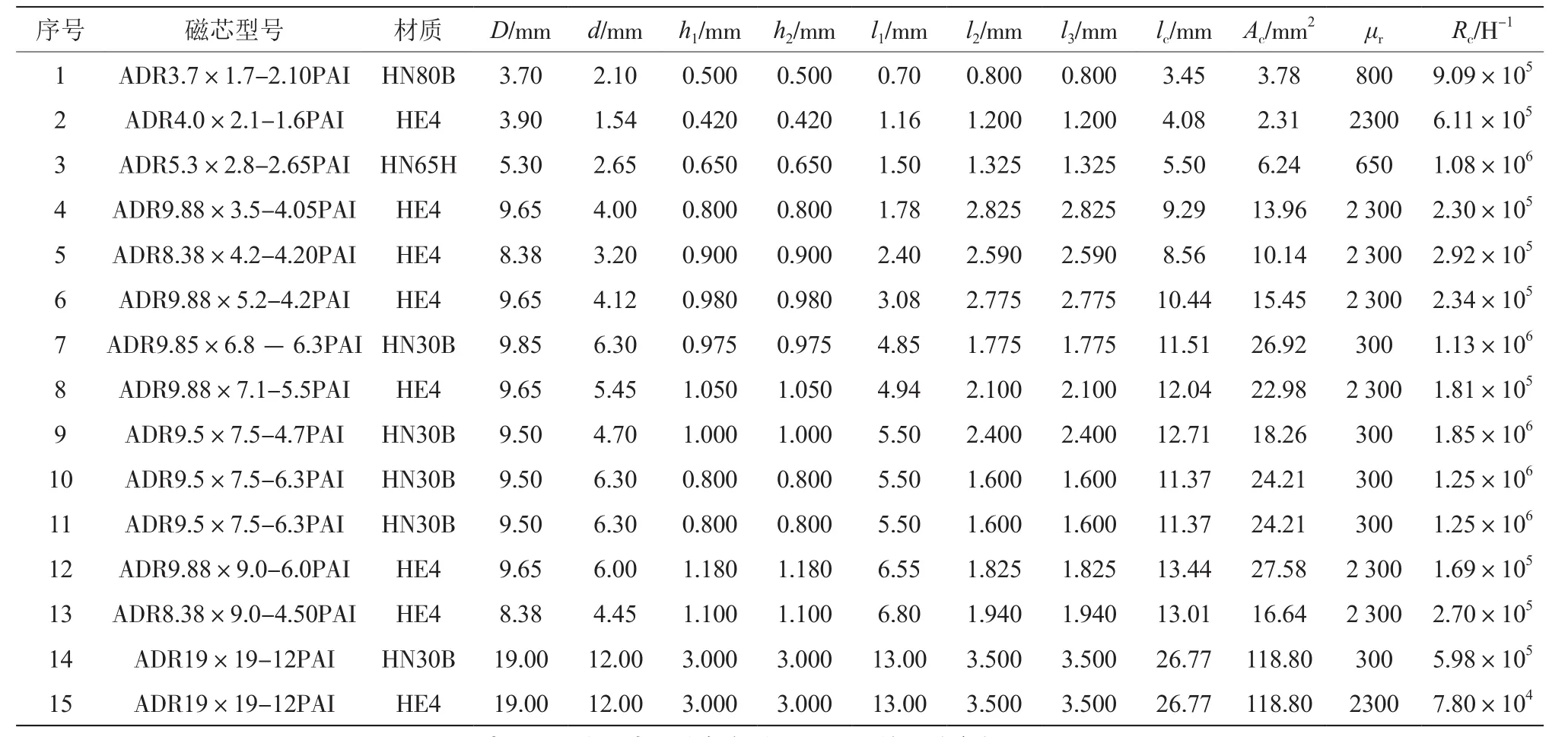
表3 工字形磁芯的尺寸测量值及有效磁路参数计算值

表4 工字形电感空气部分扩散磁通的磁路参数及磁阻
从表5中的理论电感Lc,测量电感L0对比结果可知,除了序号(组别)#2,#3的误差分别为13.90%,11.34%,其他测量误差几乎小于10%,序号(组别)#4~15的气隙lg值超过2 mm,其误差绝对值均小于5%。主要原因首先是对模型做了理想化处理,从顶部和底部溢出部分磁力线变成全部从工字形叶片边缘溢出,特别是忽略部分磁通。对于图2仿真中C区域的磁力线,当lg很大时,这一部分对磁路长度均值影响很小,但是当lg比较小时,这个对磁力线磁路长度和面积都有很大影响,导致扩散磁通磁阻计算误差变比较大,就导致#1~3序号的电感计算偏差很大。
表5中的#14和#15选用相同磁芯和相同绕组,它们之间只有材质不同,分别对应 HN30B(μr300),HE4(μr2 300),无论实测还是计算值都很接近,原因在于空气磁阻Rg数量级远远大于磁芯磁阻Rc,它们之间相差至少数百倍,磁导率之间差距对在这种工字形的电感影响很小。

表5 电感理论计算和实测验证对比
3 结 论
(1)通过验证,电感计算对于绕组完全绕满和不绕满这两种情况均适用,且证明了图4模型的正确性。
(2)绕组幅宽l1大于2 mm时,计算误差一般都在±5%之内,当l1比较小时,其误差也在15%内,工程上可满足这类电感±20%偏差要求。
(3)基于磁阻以及结合简化工字形电感的磁通模型方法推导出电感值的计算等式,把相关尺寸和对应材质的磁导率代入可得工字形的电感系数或电感值,能在极短时间内帮助开发人员设计方案和缩短开发时间。
(4)对于更多尺寸的工字磁芯绕线电感普适性和准确性还需要进一步的验证,特别是低背小尺寸工字形磁芯。

