加工参数对单晶γ-TiAl表面质量和亚表层损伤的影响机理＊

姜军强，梁桂强，孙立辉，董中奇

（1.西安科技大学 机械工程学院，西安 710054）

（2.大理大学 工程学院，云南 大理 671000）

（3.北京领航科工教育科技有限公司，北京 100084）

（4.河北经贸大学 信息技术学院，石家庄 050000）

（5.河北工业职业技术大学 材料工程系，石家庄 050000）

γ-TiAl合金作为一种新型高温合金材料，其密度低、比强度高，成为最具潜力取代镍基合金的高温轻质合金材料，并在汽车发动机、航空发动机叶片等领域得到了广泛应用[1]。工件表面质量和亚表层损伤，对工件的抗疲劳、蠕变和可靠性具有重要影响，是评价工件性能的重要指标之一[2-3]。因此，许多研究人员致力于研究切削工艺参数与表面质量之间的关系[4]。ANWAR等[5]采用涂层和未涂层刀具，通过试验研究了不同工艺参数对γ-TiAl工件表面光洁度的影响规律，发现表面粗糙度随着切削速度增加呈现先轻微减小后增大的趋势，并随着进给速度和切削深度的增加而增大。CHENG等[6]在对γ-TiAl进行车削时，发现切削速度为50 m/min，进给量不超过0.1 mm/r，切深不超过0.3 mm时，加工表面质量较好。

由于计算能力的显著提升和粒子间相互作用原始结构的确定[7]，分子动力学（molecular dynamics, MD）模拟的研究中发现：在(110)面上的[10]方向上加工成为一种有效的原子尺度范围的模拟方法。过去几十年，许多学者应用MD模拟对纳米切削做了大量工作[8]。LIU等[9]利用MD研究了单晶铜纳米切削中正四面体堆垛层错的演变过程，结果表明正四面体堆垛层错是导致工件加工硬化的主要原因之一。GUO等[10]依据分子动力学研究了纳米切削单晶铜(100)表面时的加工过程，结果表明采用相对较高的切削速度时工件内部的缺陷损伤相对较少，有利于获得较高的加工表面质量。SHIMADA等[11]证实采用相对较高的切削速度进行纳米切削模拟时，对表面粗糙度和变形层深度的影响较小。TO等[12]发现在加工{100}面单晶铝时可以获得最佳表面光洁度。REN等[13]在对单晶镍纳米磨削时，表面凸起高度最小；在(1 11)面上磨削时，亚表面变形层深度相对较小。

以上研究主要集中于单元素晶体材料纳米切削时的表面质量和亚表层损伤，而对于合金材料纳米切削时的表面质量和亚表层损伤的研究较少。因此，以MD理论为基础，进行单晶γ-TiAl合金纳米切削加工表面质量和亚表层损伤的研究，分析不同加工工艺参数对加工表面质量和亚表层损伤的影响规律。

1 MD切削模型与计算

1.1 计算模型

纳米切削模型由单晶γ-TiAl合金和非刚性金刚石刀具组成，γ-TiAl包含110 000个原子，模型沿X轴[100]、Y轴[010]、Z轴[001]方向的大小分别为18 nm×10 nm×10 nm，刀具包含9 441个原子。模型中刀具和工件都包含固定层、恒温层以及牛顿层：固定层防止切削过程中工件发生刚性位移；恒温层与外界进行热量交换；牛顿层的原子遵循牛顿第二定律，可动态追踪切削过程中原子运动轨迹并计算所需的各种物理量。周期性边界条件施加在Y方向，以消除尺寸效应。纳米切削γ-TiAl合金模型如图1所示。

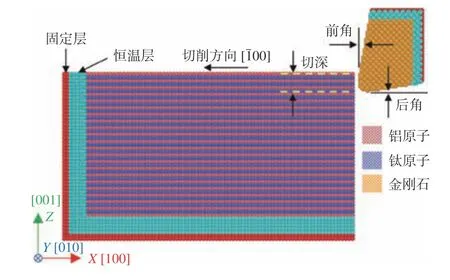
图1 纳米切削γ-TiAl合金模型示意图Fig.1 Schematic diagram of nano-cutting γ-TiAl alloy model

1.2 势函数

MD模拟中一般选用经验势函数，通过势能对原子间距求导获取原子间相互作用力Fij，见式（1）。

式 中：Fij为原子间相互作用力，Uij为势能函数，rij为原子i与原子j之间的距离。

确定粒子间作用力后，求解牛顿方程获取粒子的下一时刻运动状态。为了加速求解牛顿方程，使用velocity-verlet实现粒子运动的更新[14]。在模拟中选用3种势函数描述原子间相互作用。DAW等[15]提出的嵌入原子法(embedded atom method，EAM)在模拟计算金属结构方面具有较高精度，因此采用EAM势函数计算工件原子间相互作用，计算表达式如下：

式中：Utot是系统能量，φi,j是原子i和原子j之间的对势，Fi是 原子i的嵌入能，rij是原子i与原子j之间的距离，ρi是原子i以外的其他原子在i原子上产生的电子云密度之和，ρj表示原子j在原子i产生的电子云密度。

采用Morse势函数来计算Al–C和Ti–C之间的相互作用，Morse势的数学表达式为[16]：

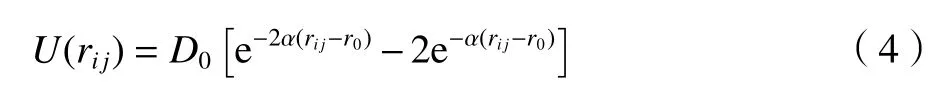
式中：U表示对势能，D0是原子结合能，α表示弹性模量，r0表示原子i与原子j之间的平衡距离。

Tersoff势函数适合于描述共价键体系原子间相互作用，常被用来计算纳米切削中金刚石刀具原子间相互作用力，其表达式如下[17]：

式中：U表示总能量，fc表示截断函数，fR表示排斥项，fA表 示吸引项，bij表示调制函数，A和B分别表示吸引项、排斥项的结合能，λ，μ表示吸引项、排斥项势能曲线梯度系数，R，D表示截断位置和宽度，β表示键级系数，ζ表示角势能，θ表示键角，c，d，h表示弹性常数。

所有模拟均依托开源软件Large-scale Atomic/Molecular Massively Parallel Simulator (LAMMPS)[18]，模拟结果通过开源软件的Open Visualization Tool(OVITO)[19]进行后处理分析。首先，对系统模型进行能量最小化消除建模过程中的不确定性；其次，系统通过Nose-Hoover弛豫控制以获取300 K平衡温度；最后，在切削过程中，牛顿层选取NVE系综，时间步长选择1 fs。表1列出了MD模拟中所用参数，采用的势函数为EAM MorseTersoff，刀具为金刚石刀具，切削方向为(0 0 1)面上的[0 0]方向。

表1 纳米切削γ-TiAl合金模拟参数Tab.1 Simulation parameters for nanomachining of γ-TiAl

2 结果与讨论

2.1 表面形貌与表面粗糙度

图2为不同切削速度下切屑表面形貌。其中，切削深度为0.5 nm，切削距离为15.0 nm，依据原子Z向堆积高度赋予原子颜色值。从图2中看出：切削速度增加会导致刀具前端堆积的切屑原子体积增大。切削距离增加会导致工件内部产生晶格缺陷，诱发位错形核，该过程中大量位错形核并沿(111)滑移面滑移[20]。从图2中还可以看出：当切削速度超过100 m/s时，刀具前端切屑体积只发生了轻微增大。这表明γ-TiAl的材料加工效率在切深一定时随着切削速度的增加会达到临界值。这主要是因为切削速度增加，使得工件温度和势能增加，高温不可避免地会降低晶体的结合键能。因此，随着切削速度的增加，材料加工效率得到提升。由于材料的塑性变形的传播以及晶格振动驱动源惯性作用的有限性，随着切削速度的增加，材料加工效率达到临界值。

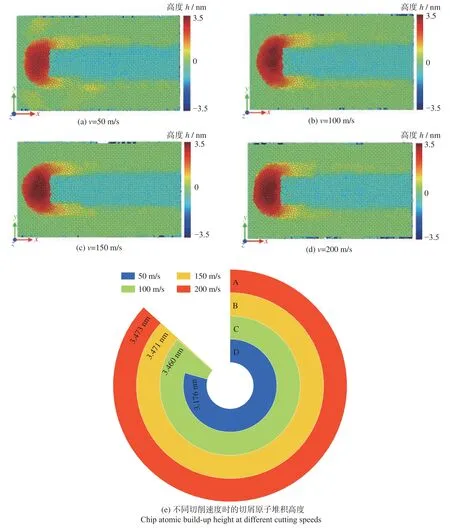
图2 切削速度对表面形貌的影响Fig.2 Influence of cutting speeds on surface morphology

图3为切削速度50 m/s时，切深对刀具前端切屑堆积的影响。从图3中可以看出：随着切深的增加，堆积在刀具前端的切屑原子数和堆积高度呈现正相关趋势。这主要是切深增加导致刀具与工件的接触面积增大，刀具对工件做的功增大，使得刀具前端更多的原子键断裂形成切屑。加工参数对表面形貌的影响与先前研究结论一致[20-21]，即材料加工效率随着切削深度的增加而得到提升，随着切削速度的增加在一定程度上也得到提升，但存在切削速度临界值（即切削速度增加对加工效率的影响程度存在界限）。

图3 切深对刀具前端切屑堆积的影响Fig.3 Influence of cutting depths on chip accumulation at the front of the tool

表面粗糙度是评价表面质量关键指标之一[22-23]。在纳米切削中，刀具和工件作用处产生位错，部分位错穿透工件向下运动，刀具通过后位错回弹在工件表面形成原子台阶，原子台阶的高度称为表面粗糙度[11]。由于γ-TiAl工件表面均匀平整，采用表面轮廓算术平均偏差Ra表征加工表面粗糙度，计算公式表述为[24]：

式中：lr是采样长度，yi表示采样点偏离平均平面的高度。

相比于二维表面粗糙度参数，三维表面粗糙度参数更加综合和精确反应已加工表面轮廓。因此，采用评估表面轮廓的三维表面粗糙度参数Rq来计算表面粗糙度，计算公式为[24]：

图4为加工参数对已加工表面粗糙度的影响。图4a中切削速度分别为50，100，150，200 m/s，切深为0.5 nm。图4b中切削深度分别为0.5，1.0，1.5 nm，切削速度为50 m/s。图4a表明：随着切削速度的增加，表面粗糙度呈现出了先减小后增大的趋势，从50 m/s到150 m/s时，Ra和Rq连续减小，但100 m/s时的表面粗糙度与150 m/s时的相差不大。这表明纳米切削γ-TiAl存在切削速度临界值，即切削速度增加对表面粗糙度的影响程度存在界限，这与图2结果一致。当切削速度增加时，表面粗糙度减小的原因在于表面粗糙度与位错紧密相关。切削速度增加，原子重排时间变短，位错未来得及穿透工件向下运动就以原子团簇的形式形成切屑被去除。随着切削速度的继续增加，表面粗糙度增大的原因在于切削速度的增加导致温度和动能增加，高温导致工件原子的成键能力弱化，同时会造成刀具磨损，进而导致黏附效应增强，因此表面粗糙度增大[10]。从图4b中可以发现：切削深度的增加导致表面粗糙度的显著增大，这是由于切深增加，应力增大以及单原子的切削厚度增加，应力增大引起位错发射进而导致表面粗糙度增大。与图4a对比发现，切深对表面粗糙度的影响程度大于切削速度。AL-AHMARI等[25]在对γ-TiAl合金宏观切削时，发现切削速度增加，表面粗糙度呈现出了先减小后增大趋势，且切深对于表面粗糙度影响要大于切削速度的。

图4 加工参数对表面粗糙度的影响Fig.4 Influence of machining parameters on surface roughness

2.2 静水压

在纳米切削中，刀具和工件的复杂相互作用，使得工件内部存在高压应力，内部应力的存在与位错形核和发射密切相关。离散状态下的原子应力状态采用维里应力进行表征，原子维里应力由公式（14）计算得出[26]。

将计算得到的维里应力值代入公式（15）得到工件内部的静水压分布[27]。

式中： σhy(i) 为原子i的静水压，σxx(i)、 σyy(i)、 σzz(i)分别为原子i沿xx、yy、zz方向的应力。

图5为不同切削速度和切深下的工件静水压分布状态。图5a、图5b、图5c、图5d分别表示切深为0.5 nm，切削距离为9.0 nm，切削速度为50，100，150，200 m/s时的工件内部静水压分布，图5e、图5f分别表示在切削速度为50 m/s，切削距离为9.0 nm，切深为1.0，1.5 nm时的工件的静水压分布。

图5 不同切削速度和切深下的工件静水压分布状态Fig.5 State of hydrostatic pressure distribution in the workpiece at different cutting speeds and cutting depths

从图5中可以看出：高静水压位于与刀尖圆弧接触的区域，工件静水压以切屑根部为中心，呈同心扇形状向工件和切屑内部梯度递减分布。从图5a、图5b、图5c、图5d可以发现：切屑根部与刀尖圆弧接触区域的压缩静水压的幅值和面积随着切削速度的增加而增大。从图5a、图5e、图5f可以发现：随着切深的增加，切屑根部的高压缩静水压的幅值和面积都表现出递增的趋势。HOSSEINI等[27]在对晶体铜进行纳米切削时发现：工件内部最高压缩静水压位于切屑根部，并且呈圆弧形散射到工件内部，并梯度递减 ，该结果与本研究具有一致性。

2.3 位错与相变

纳米切削中，高温高压减小了位错形核及发射的能量势垒，导致位错损伤产生，对材料力学性能产生重要影响[9]。图6a、图6b、图6c、图6d分别表示切深在1.0 nm，切削距离为11.2 nm，切削速度为50，100，150，200 m/s时，工件内部位错线分布情况；图6e、图6f分别表示在切削速度为50 m/s，切深为0.5，1.5 nm时工件的位错线分布。图6中颜色依据计算的位错提取分析DXA值，其中红色线是Other位错，粉红色线是Stairrod位错，绿色线是Shockley位错，黄色线是Hirth位错，深蓝色线是Perfect位错，浅蓝色线是Frank位错。

从图6a可以看出：位错主要分布在刀具前方和下方，另外在刀具前方沿0]方向也存在位错分布。沿方向分布的2个Shockley不全位错相互作用生成一个全位错Perfect。从图6a还可以看出：刀具下方存在Shockley不全位错、Frank部分位错、Stair-rod位错以及Other位错。Frank部分位错是由一系列位错反应生成的[28]。Stair-rod位错难于移动，会产生钉扎效应导致加工硬化产生[29]。对照图6a、图6b、图6c、图6d发现，Shockley不全位错在位错机制中占主导地位。这是由于不全位错形成所在的(111)面是一个压缩面，在相对较小的剪切应力作用下便可滑动。随着切削速度的增加，工件内部的位错类型复杂程度降低，位错密度呈现出减小的趋势。这是因为在切削速度小于塑性波在材料中的传播速度时，形核后的位错有充足的时间和能量进行位错滑移和相互作用，形成复杂位错结构；而在高速切削时，位错形核后未来得及充分发展便发生湮灭。为定量化对照不同切削速度下工件内部位错密度差异，采用位错密度式（16）计算工件内部位错密度[30]。

图6 不同切削速度和切深下的工件内部的位错分布Fig.6 Dislocation distribution in the workpiece at different cutting speeds and cutting depths

式中：ρ为位错密度，∑L表示位错线长度，V为体积。计算得到切削速度为50，100，150，200 m/s时的位错密度分别为1.336%，0.566%，0.376%，0.279%。

从图6a、图6e、图6f看出：在相同切削速度下，随着切削深度的增加，工件内部的位错数量、位错类型复杂程度以及位错长度都呈现出正相关关系。这是因为切深增加导致工件高温区域扩大，刀工接触时间增长，位错形核和发射的能量势垒降低，工件原子获得足够多的变形能，位错有更多的时间进行发射和相互作用。通过式（16）定量计算0.5，1.5 nm切深下工件内部的位错密度分别为0.621%，2.429%。

图7a、图7b、图7c、图7d 分别表示切深为1.0 nm，切削速度为50 m/s，切削距离为1.3，6.0，6.8，15.0 nm时的工件内部缺陷损伤，采用的是EAM势函数。图7中颜色依据计算得到的共近邻分析CNA(common neighbor analysis)值进行染色，CNA依据特定原子对成键和近邻原子列表信息识别材料缺陷及局部晶体结构状态，其中白色代表非晶态原子包括表面原子、位错原子和空位原子，蓝色代表CNA值为2的体心立方晶格（BCC）原子，红色表示CNA值为3的密排六方结构（HCP）原子。为清晰观察，删除了CNA值为1的面心立方晶格原子。从图7a可以看出：初始切削阶段由于刀具对工件的剪切挤压作用，迫使工件发生相变，由面心立方（FCC）结构转变为BCC和HCP以及其他结构类型，并在(111)面上产生内禀堆垛层错。其产生的来源在于Shockley不全位错在(111)上形核后的增殖扩展运动，堆垛层错的出现增加了刀具的进给力和工件抗应变能力以及塑性变形程度。图7b中，刀具前方45o方向存在V形位错环和梯杆位错。V形位错的产生是由于2个不全位错形核后沿着各自的伯格斯矢量增殖扩展，发生相遇相互阻碍而形成的位错锁[31]。梯杆位错是位错形核增殖过程中，由1层或几层原子缺失或错动而形成带有台阶的线性位错缺陷[29]。随着刀具的继续切削到图7c时，在刀具的持续作用下刀具前方的梯杆位错和V形位错结构被破坏，形成稳定的空位缺陷和原子团簇残留在工件内部，这表明刀具持续作用的能量大到足以克服抗塑性变形能。从图7d可以看出：切削进入到后期阶段时，刀具对变质层的影响相对较小，刀具过后由于工件的弛豫使得工件内部部分弹性变形得以恢复和部分晶格重构，导致工件内部位错形核幅度减小以及工件内部缺陷大部分湮灭，同时在亚表层残留一些稳定的空位和原子团簇缺陷损伤影响材料性能及残余应力。从图7中还发现：已加工表面处非晶原子排列紊乱并未呈现规则状态，且非晶原子占据了结构相变原子的绝大部分比例。因此非晶原子数目一定程度上表明了结构塑性变形的程度。计算切削距离为15.0 nm，切深为1.0 nm，切削速度为50，100，150，200 m/s时的非晶原子数目分别为4 711，5 242，5 314，5 696。计算切削距离为15.0 nm，切削速度为50 m/s，切深为0.5，1.0，1.5 nm时的非晶原子数目分别为3 090，4 711，5 648。计算结果表明随着切削速度和切深的增加，工件塑性变形程度展现出同步递增趋势。

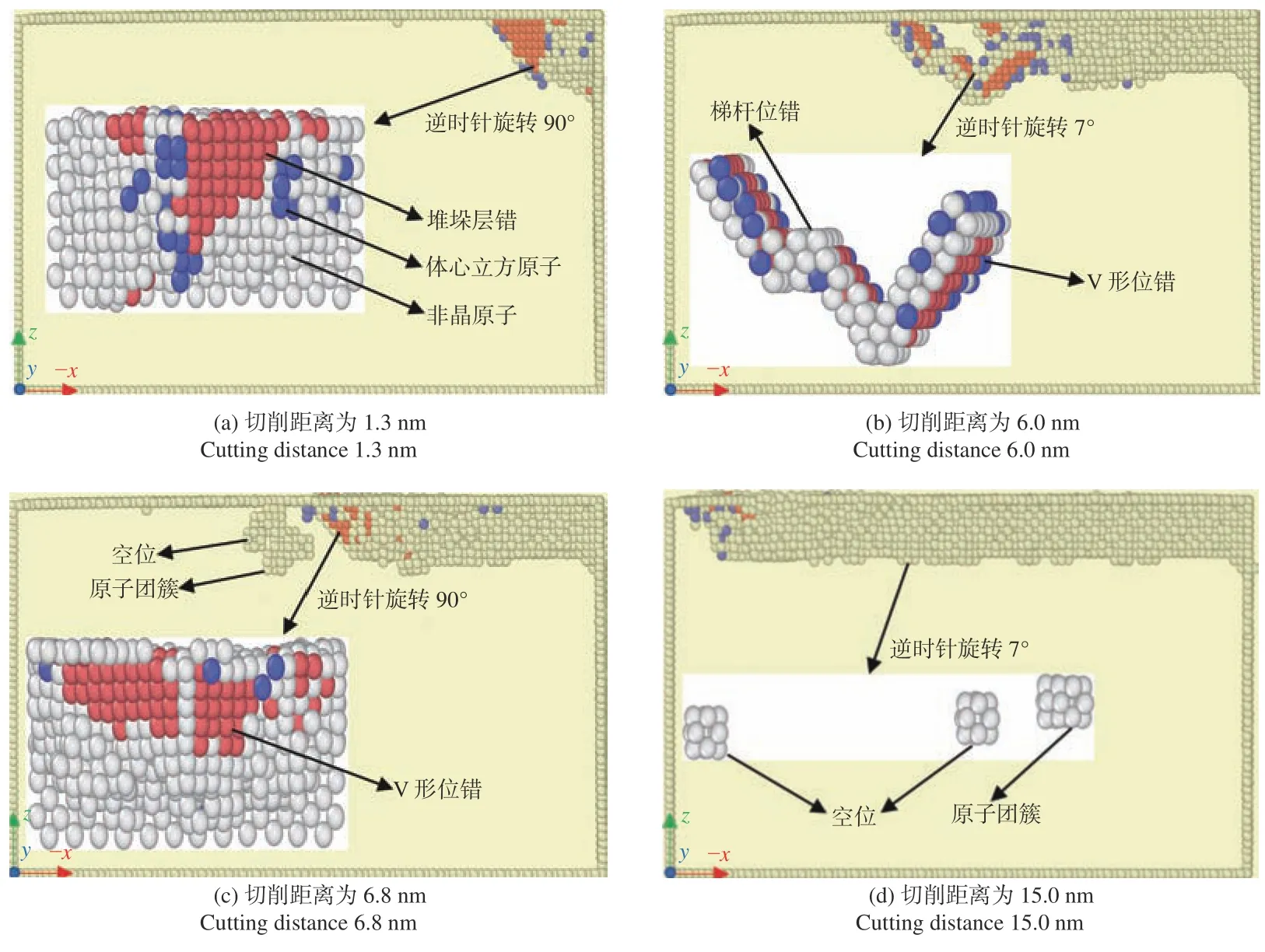
图7 切削加工中缺陷演化过程Fig.7 Evolution of defects in the workpiece during cutting process

3 结论

以分子动力学为基础研究了不同切削速度和切深对非刚性金刚石刀具纳米切削γ-TiAl合金表面质量和亚表层损伤的影响，并得到以下结论：

（1）切削速度增加，切屑体积增大和材料加工效率提升，但存在切削速度为100 m/s时的临界值。表面粗糙度随着切削速度的增加呈现出先减小后增大的趋势，且切削速度对表面粗糙度的影响存在切削速度为100 m/s时的临界值。切深增加切屑体积增大，材料加工效率提升，表面粗糙度显著增大。

（2）高静水压位于切屑根部与刀尖圆弧接触区域，呈同心扇状向工件和切屑内部梯度递减分布。随着切削速度和切深的增加，高压缩静水压的幅值和面积都表现出递增趋势。

（3）Shockley不全位错在位错机制中占主导地位, 切削过程中存在V形位错以及梯杆位错，并且在切削完成后，工件内部存在空位和原子团簇等稳定缺陷。随着切削速度的增加，位错类型的复杂程度降低，位错密度呈减小趋势，不过切深的增加却导致相反趋势；切削速度和切深增加，非晶原子数增多，塑性变形程度增加。