灰色GM(1,1,k,k2)模型背景值及时间响应函数优化
孔新海, 陈佳佳, 赵 勇
(广安职业技术学院,四川 广安 638000)
0 引言
灰色系统理论于1982年被邓聚龙教授首次提出,现已广泛应用于许多领域,比如工业管理、农业生产、能源交通等领域,其最核心理论是灰色预测模型,特别是GM(1,1)模型[1]。然而在应用过程中,有学者就不断发现GM(1,1)模型仅对光滑的原始数据序列建模效果较好,而其他数据建模精度不是很高,会出现误差较大的情况,应用范围受到限制。于是学者们就从不同视觉来完善和拓广GM(1,1)模型,综合当前对灰色模型研究情况来看:一是优化灰色模型本身,提高模型模拟预测精度,比如优化GM(1,1)模型的灰导数[2]、背景值[3]和初始值[4],以及改变累加方法[5]等;二是提出新的灰色模型,拓广模型应用范围,比如提出离散DGM(1,1)模型[6,7]、NGM(1,1,k)模型[8]、ENGM(1,1,k)模型[9]、NGM(1,1,tα)模型[10,11]、DGM(1,1,tα)离散模型[12]、基于离散余弦变换的GM(1,1,d)模型[13]等。这些优化方法和新灰色模型都极大地提高和拓广了灰色模型建模精度和应用范围,使得灰色理论得到快速发展和壮大。但文献[14]研究结果显示,仅优化GM(1,1)模型本身只能提高模型精度,不能改变模型适用于下凸序列建模的事实;而上述提出的新灰色模型一定程度上拓宽模型应用范围,但新模型仅含一个时间项,通过分析发现建模精度不是很高。因此,本文提出一种新的带有时间次项的灰色GM(1,1,k,k2)模型,该模型包含一次时间幂和二次时间幂,并优化灰色GM(1,1,k,k2)模型的背景值,给出模型参数辨识方法和最优的时间响应函数。
1 灰色GM(1,1,k,k2)模型
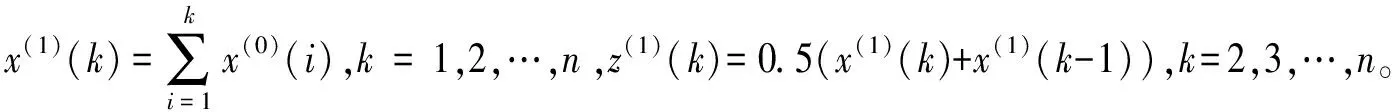
x(0)(k)+az(1)(k)=bk2+ck+d
(1)
为含有时间一次幂和时间二次幂的灰色GM(1,1,k,k2)模型的基本形式。
显然当b=0时,即退化为非齐次灰色NGM(1,1,k)模型[8];当c=0时,即退化为灰色GM(1,1,t2)模型[10];若b=0且c=0,即退化为传统灰色GM(1,1)模型。
定理1根据最小二乘法,灰色GM(1,1,k,k2)模型参数估计值为
(2)
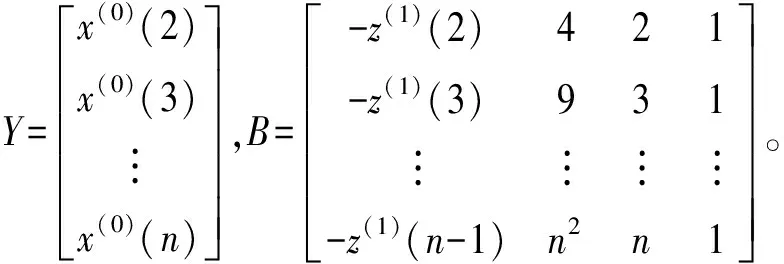
证明以-az(1)(k)+bk2+ck+d代替,x(0)(k),k=2,3,…,n,可得误差序列ε=Y-Bα,记
s=εTε=(Y-Bα)T(Y-Bα)
为使误差平方和s最小,参数a,b,c,d应满足
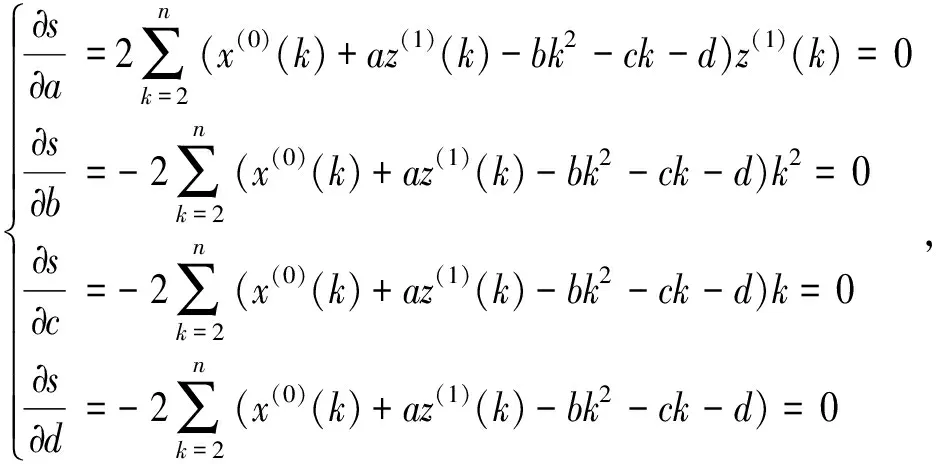
定义2称微分方程
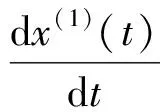
(3)
为灰色GM(1,1,k,k2)模型相对应的白化微分方程。
采用常数变易法对白化微分方程(3)式进行求解,可解得其时间响应函数为
(4)
这里常数C为待估参数。
若初始值取x(1)(1)=x(0)(1),则
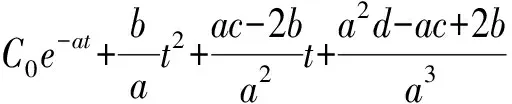
(5)

对(5)式离散化之后为
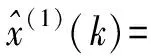
(6)
因此,灰色GM(1,1,k,k2)模型的还原值为
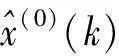
(7)
2 灰色GM(1,1,k,k2)模型的背景值优化
2.1 背景值优化
对(3)式在区间[k-1,k]进行两边积分,有

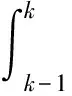
(8)
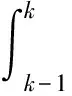
(9)
把(9)式记为
(10)
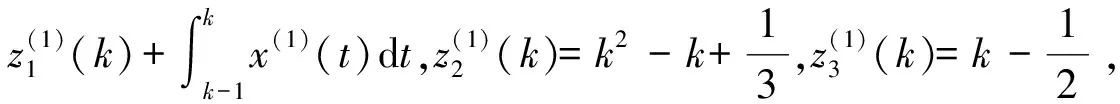
(10)式与(1)式相比,背景值发生了变化,即
从而使得背景值优化后的灰色GM(1,1,k,k2)模型与其白化微分方程具有一致性。同理,采用最小二乘法,可得(10)式参数估计值为
[a,b,c,d]T=(CTC)-1CTY
(11)
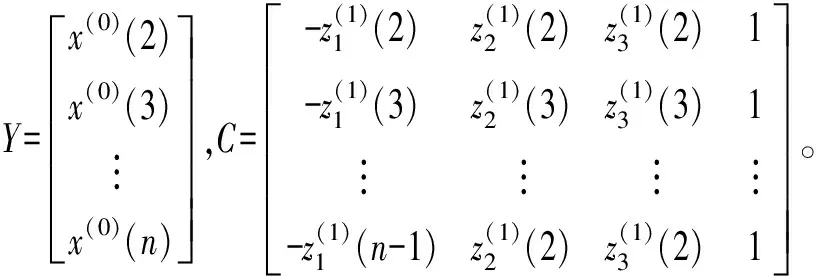

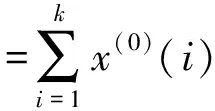
(12)
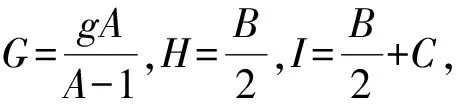
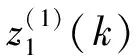
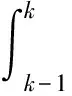
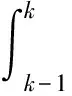
(13)
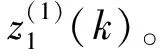
(1)第一种情况:

(14)
其参数计算方式如下:
(2)第二种情况:

(15)
其参数计算方式如下:
(3)第三种情况:
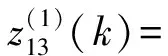
(16)
其参数计算方式如下:
(17)
2.2 时间响应函数优化
由前面(4)式和(7)式可以知道,灰色GM(1,1,k,k2)模型的还原式为
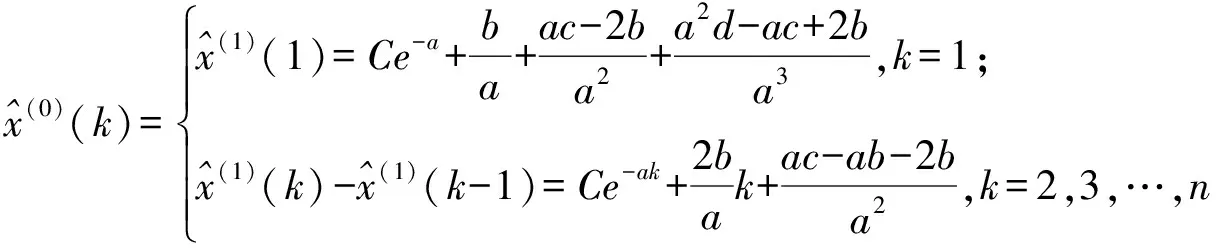
(18)
这里C为待估常数。
为了确定常数C,取还原值与原始序列误差平方和最小为目标函数,即
(19)
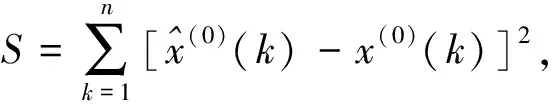

两边对C求导,并令导数等于0,可解得
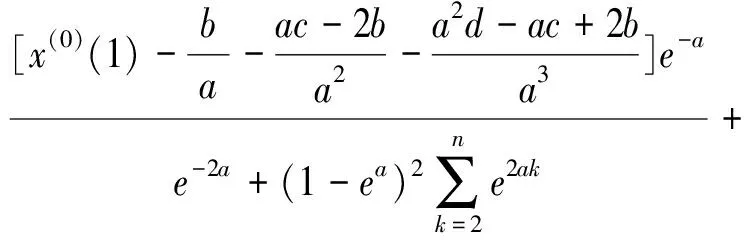
(20)
所以,优化初始值后的GM(1,1,k,k2)模型还原式为
(21)
根据以上分析,可以归纳GM(1,1,k,k2)模型建模基本步骤如下:
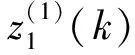
Step2根据(11)式估算参数a,b,c,d的值;
Step3利用(20)式求得优化初始值C*;
Step4把上述求解结果,代入(21)式可得原始时间序列的模拟值和预测值。
3 模型应用
某软土地基间隔10天测得沉降数据为:x=[70.87,83.71,92.91,99.73,105.08,109.73,112.19,113.45][15],单位:cm。分别选取前7个数据作为建模数据,最后1个数据作为模型预测检验数据,建立灰色GM(1,1,k,k2)模型。为便于计算,这里采用MATLAB软件进行编程计算模型参数。根据(11)式可计算得到优化背景值后的灰色GM(1,1,k,k2)模型参数估计值为
a=0.0986,b=-0.35,c=18.7998,d=67.5116
把a、b、c、d估计值代入(20)式,得到C*=1976.5074,从而同时优化背景和时间响应函数的灰色GM(1,1,k,k2)模型为

-7.0987k+197.7576,k=2,3,…
其模拟预测计算结果见表1。
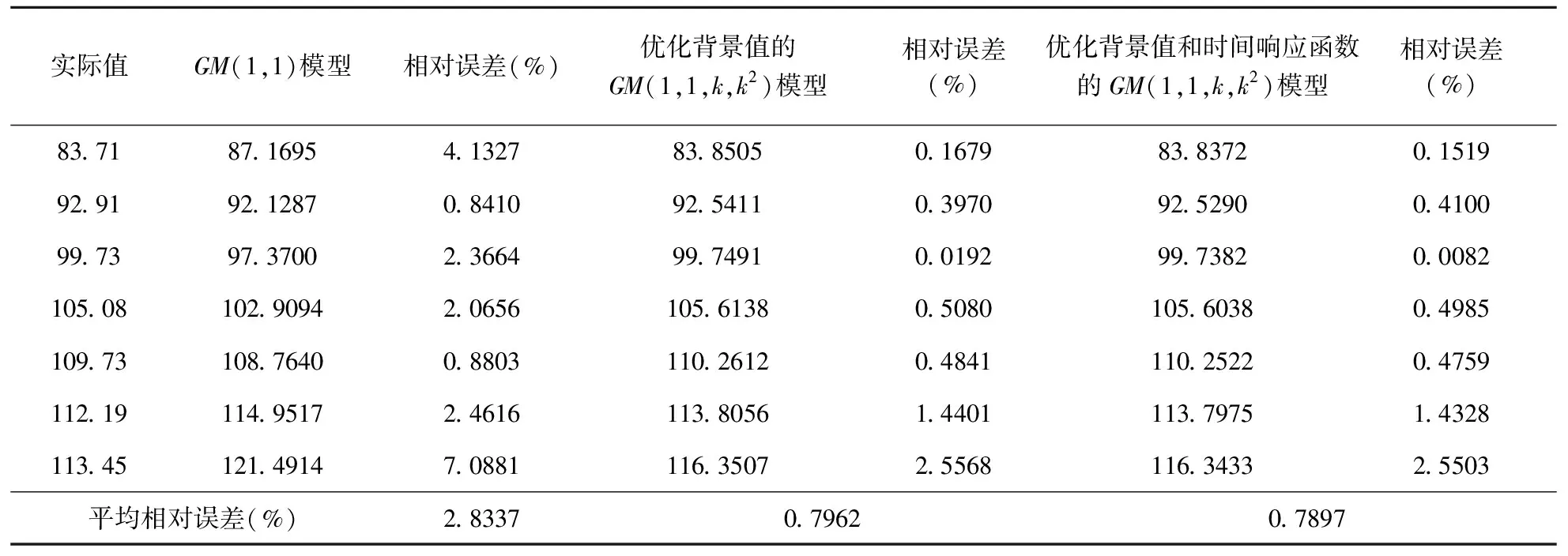
表1 灰色GM(1,1)模型与GM(1,1,k,k2)模型建模效果比较

图1 几种灰色模型效果比较
从表1和图1能够看出,优化背景值的GM(1,1,k,k2)模型与同时优化背景值和时间响应函数的GM(1,1,k,k2)模型建模效果较好,预测结果与原始时间序列发展趋势基本保持一致。但灰色GM(1,1)模型预测序列发展趋势发生变化,呈下凸形状,不适合上凸时间序列建模。
4 结语
本文建立的灰色GM(1,1,k,k2)模型是一个同时含有一次时间幂次项和二次时间幂次项的灰色模型,根据选取的实例可以看出,其拟合预测效果较佳,可以用于短期预测。同时看出,GM(1,1)模型仅适用于下凸时间序列建模,如果模型增加时间幂次项,则还可以适用于预测上凸时间序列,大大拓广了模型适用范围。对于进行背景值优化的GM(1,1,k,k2)模型的计算至少需要原始数据6个,而且数据最好是成上凸序列或下凸序列。如果不是,则(14)~(16)式参数计算必须取平均值且参数A大于零。

