范数下无容量限制设施选址逆问题的求解方法

李子慷, 刘林冬, 于成成

(中国科学技术大学 管理学院国际金融研究院,安徽 合肥 230026)

0 引言

最基本的设施选址问题分为无容量限制和有容量限制两种。其中无容量限制设施选址问题(Uncapacitated Facility Location Problem, UFLP)在文献中得到了广泛的讨论[1]。Krarup对研究UFLP问题的文献进行了综述，并指出了UFLP问题是NP-难的[2]。逆优化问题最初由Tarantola给出了逆优化问题在地球物理科学中的详细讨论[3]。Heuberger给出了关于逆优化问题较为全面的综述[4]。Ahuja和Orlin证明了在范数L1和范数L∞下，如果原线性规划问题多项式可解则其逆问题也是多项式可解的[5]。通常来讲，只有逆问题的可行域是一个多面体，才能确保在范数L1下的逆问题在多项式时间内是可解的[6]。Schaefer给出了一般整数规划逆问题的多面体描述，并提出了两种算法求解[7]。

由于设施选址逆问题在一般网络下，大多数是NP-难的，很多学者考虑了特殊情况下的逆选址问题。Cai等人考虑了逆单中心选址问题，证明了即使在单中心选址原问题是多项式可解的情况下，逆单中心选址问题仍然是NP-难的[6]。Alizadeh等人考虑了在树状图中边长度仅允许增加时的逆单中心选址问题，给出了一个时间复杂度为O(nlogn)的精确算法[8]。Guan给出了在加权L∞范数下，逆1-中值选址问题线性时间算法，并证明了在加权哈明距离下该逆问题是NP-难的[9]。

在逆选址值问题上，Berman等人证明了在二分网络中的逆选址值问题是NP完全的，同时给出了在树形网络中该问题的线性表达式[10]。Zhang等人研究树形网络中的逆选址值问题，并给出了一个时间复杂度为O(n2logn)的多项式时间算法，同时提出该问题的变体，证明了逆多设施选址值问题可以转化为几个逆单设施选址值问题[11]。

设施选址逆问题具有潜在的应用前景，它为我们展示了如何花费尽可能少的成本，从而固定开启某些现有设施以提供便利。对应到模型中，即给定了开设哪些设施，这些设施对哪些顾客进行服务，目标函数则为使得设施和运输成本改变量达到最小。因而研究最基本的无容量限制设施选址逆问题及其求解算法是十分具有现实价值的。

本文研究了无容量限制设施选址逆问题(Inverse Uncapacitated Facility Location Problem，IUFLP)模型的建立与求解方法。用行生成算法将IUFLP问题分为主问题和子问题，其中子问题为一般的无容量限制设施选址问题(UFLP)。对子问题进行不同的处理方式，可以分别得到IUFLP问题的上下界。

本文安排如下：第一节给出了UFLP的定义以及IUFLP模型的建立。第二节给出了IUFLP的行生成求解方法。第三节对由行生成算法得到的子问题进行了改进，得到能求出该逆问题上下界的启发式算法。第四节给出了IUFLP的简单示例以及计算结果。第五节给出了对于该逆问题延拓以及算法改进的展望。

1 UFLP和IUFLP问题的模型

设施选址问题通常有如下的定义：假设有m个设施和n个顾客。我们希望选择(1)哪些设施要打开，以及(2)哪些打开的设施要用于向哪些顾客提供服务，以便以最低的成本满足需求。引入以下记号，令fi表示开启设施的固定成本，i∈M,M={1,…,m}。rij表示运输商品从设施i到顾客j的成本，j∈N,N={1,…,n}。无容量限制指每个设施可以提供的容量K是充分大的。

设为fi维m的行向量，将rij按行首尾相接为一个(m×n)维的行向量，则可用一个(m+m×n)维行向量c=(f,r)表示成本。

则无容量限制设施选址问题(UFLP)定义如下:

uij,vi∈{0,1},∀i∈M,∀j∈M

用更为简洁的方式改写包含足够大容量K的上式，得到下式:

uij≤vi,∀i∈M,∀j∈N

uij,vi∈{0,1},∀i∈M,∀j∈N

在上述整数规划模型中，uij表示顾客j是否被设施i所服务，如果被服务，则uij=1，否则uij=0；vi表示设施i是否开启，如果开启，则vi=1，否则vi=0。(1)式为UFLP的目标函数，要使得开启设施和运输商品的总成本最小；(2)式表示每个顾客j∈N必须被一个设施所服务；(3)式表示如果顾客j被设施i所服务，则设施i必须开启。

逆问题通常有如下的定义，当给定一个加权优化问题和一个固定可行解的实例，其相应的逆问题就是尽可能少地(在一个固定范数下)修改加权参数，使得给定的解在该实例中成为原优化问题的最优解。

根据逆问题的定义，一般优化问题的逆问题有如下形式：

mind‖d-c‖

s.t.d∈G(x0)

G(x0)={d∈Rn

|min{g(d,x)|∈D}=g(d,x0)

其中g(c,x)为原优化问题的目标函数，c∈Rn为参数向量，D为x的可行域，d∈Rn为调整后的参数向量。G(x0)表示使给定的可行解x0成为g(d,x0)最优解的参数向量d的集合。

则L1范数下无容量限制设施选址的逆问题(IUFLP)可以定义如下:

minw×|d-c|T

s.t.dx0=U(d)

d∈Rm+mn

其中w=(wf,wr)为(m+mn)维行向量，d=(f0,r0)为调整成本后的(m+mn)维行向量，f0,r0分别表示调整之后的设施成本和运输成本，c=(f,r)为上述的原成本参数，|d-c|T为成本调整量(绝对值)的(m+mn)维列向量，x0为给定原问题的一个可行解，U(d)为(1)式中参数为d时对应的最小值。

由约束式可以看出，x0是满足调整成本后UFLP所有约束的最优解。对于每一个顾客j∈N可以被任一设施服务，共有|M|=m种选择。因而对于所有顾客而言一共会有mn种不同情况。即满足UFLP约束条件的可行解有mn个。同时定义满足UFLP约束条件的mn个可行解构成的解集为Y。因此从逆问题的定义出发建立求解模型，Y中包含可行解的个数是指数个。事实上，无容量限制设施选址的逆问题(IUFLP)是NP-难的。

定理1无容量限制设施选址的逆问题(IUFLP)是NP-难的。

2 行生成算法求解

从上述无容量限制设施选址逆问题的定义过程中，我们可以看出原优化问题和其逆问题有着一定的联系，即逆问题中的给定解对应的成本需要小于等于所有满足原问题约束条件的解对应的成本。行生成算法作为一种有效求解规模较大线性规划问题的方法。我们可以将行生成算法应用于该问题中，并且容易发现此时的子问题即是UFLP原问题，因而行生成算法可以用来求解无容量限制设施选址的逆问题。

无容量限制设施选址的逆问题模型为:

∀j∈N,(v′,u′)∈Y

其中Y同上述，是满足原问题的所有可行解x′=(v′,u′)的集合。为方便显示我们的结果，我们主要考虑逆最优解问题，即逆问题。而对于逆最优值问题，即给定V0而不是x0，根据式V0=cx0也可用相同思路求解。下文只针对逆问题进行分析求解。

将行生成算法应用于IUFLP，将c对应的设施和运输部分用(f,r)分别表示。根据Ahuja在L1范数下逆问题的处理方法[5]，记c=(f,r)为原成本向量，d=(f0,r0)为调整后的成本向量。令

则ai,hij分别表示相对原成本的增加量，fi,rij表示相对原成本fi,rij的减少量。

可以得到IUFLP的主问题为:

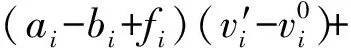
∀i∈M,∀j∈N

ai≥0,bi≥0,∀i∈M

hij≥0,lij≥0,∀i∈M,∀j∈N

(v′,u′)∈Ⅱ

其中(v′,u′)属于一个可行解限制集Ⅱ⊂Y，限制集中的元素由子问题不断生成加入其中。而主问题得到的(a′,b′,h′,l′)在每次迭代循环中带入到子问题中求解。

子问题如下:

子问题求出得到(v′*,u′*)，如果目标函数值小于0，将得到的(v′*,u′*)加入到主问题的限制集中。如果目标函数值不小于0，程序结束。注意到子问题实际上就是UFLP。

求解IUFLP问题的行生成算法详细步骤如下:

输入：1)可行解：x0=(v0,u0)； 2)原设施成本：c=(f,r)；

输出：1)最优解：(a*,b*,h*,l*)；2)最小的总成本改变量：

3)对应原成本的改变量：

初始化：初始限制集包含对于原问题的可行解即可。为方便且不再重新生成可行解，可取初始限制集为只含给定的可行解这一个元素的集合即I0={(v0,u0)}。

步骤1求解此时的主问题得到最优解(a′,b′,h′l′)。

步骤2将步骤1得到的最优解(a′,b′,h′l′)带入到子问题中，求解子问题这一整数规划得到最优解x′*=(v′*,u′*)和目标函数值T。

步骤3如果目标函数值T<0，将得到的x′*加入到限制集中，Ⅱ=Ⅱ∪{x′*}回到步骤 1，重新求解主问题；如果目标函数值T≥0，则结束算法，得到最终的限制集，记为ⅡI。根据此限制集ⅡI求解主问题，即可得到最优解(a*,b*,h*,l*)。

3 启发式算法得到上下界

由上述的行生成方法，我们可以知道要求得逆问题的最优解就需要得到尽可能精确的主问题的限制集，即主问题中的约束条件。由于主问题的限制集是由子问题不断生成得到的，可以看出行生成方法的核心是子问题的求解效率，即子问题求解越精确，逆问题的最优解越精确。但由于子问题是设施选址的原问题，因而可以通过对子问题进行松弛，牺牲一定求解精度的情况下简化求解过程。

当对子问题进行如下几种处理方法时，我们可以相应得到行生成方法的几点结论：

处理方法1：严格求解子问题(S)。

定理2当严格求解子问题时，循环结束时此时得到IUFLP的最优解。

说明：注意到从子问题中筛选出的解的数量依赖于给定的初始解，虽然行生成方法可以极大地减少原有的约束，但究竟需要筛选出多少解是无法判断的。事实上，如果可以判断出能够筛选出多少解，根据筛选出的解构成的解集直接求解主问题就可以解决IUFLP。

处理方法2：对子问题利用邻域搜索方法得到启发式整数解，同时设置一定的循环次数提前终止子问题的求解。

定理3对子问题利用邻域搜索方法求解，并且设定一定的循环次数提前终止子问题的求解，此时求解得到IUFLP的下界。

对于利用邻域搜索求解子问题的说明：邻域搜索采用基本的本地搜索方法[12]，即对于当前给定解采用增加，交换和减少的方式得到局部最优整数解。

下面对邻域搜索的三种方式进行说明。设此时未开启设施的数量为p，开启设施的数量为(m-p)。增加，即对于当前未开启的设施中开启一个设施，作为一个增加邻域，共有p个邻域。交换，即对于当前未开启的设施中开启一个设施，在开启的设施中关闭一个设施，作为一个交换邻域，共有p(m-p)个邻域。减少，即对于当前开启的设施中关闭一个设施，作为一个减少邻域，共有(m-p)个邻域。

在一次求解过程中，对于三种方式得到的邻域解对应的成本进行比较，取最小值求得对应的局部最优解。将当前给定解转移到得到的局部最优解，同时将该局部最优解加入到主问题的限制集中，再进行下一次求解。

求解UFLP下界的启发式算法详细步骤如下：

输入：1)可行解：x0=(v0,u0)；2)原设施成本：c=(f,r)；

输出：1)最优解：(a*,b*,h*,l*)；2)最小的总成本改变量：

3)相对原成本的改变量：

初始化：初始限制集包含对于原问题的可行解即可。为方便且不再重新生成可行解，可取初始限制集为给定的可行解即Ⅱ={(v0,u0)}。

步骤1求解此时的主问题得到最优解(a′,b′,h′,l′)。

步骤2将步骤1得到的最优解(a′,b′,h′,l′)带入到子问题中，邻域搜索的子问题目标函数与前述保持一致，对给定的初始解采用增加，交换，减少操作得到局部最优解x′*=(v′*,u′*)和目标函数值T。

步骤3如果目标函数值T<0，将得到的x′*加入到限制集中，Ⅱ=Ⅱ∪{x′*}回到步骤1，重新求解主问题；如果目标函数值T≥0，则结束算法。此时得到最优解(a*,b*,h*,l*)。

其中邻域搜索中的增加，交换，减少操作如图1所示：

图1 邻域搜索对当前解进行三种操作的示意图

处理方法3：对子问题(S)进行线性松弛求解。

定理4将子问题(S)进行线性松弛得到线性规划问题，使用行生成算法求解则可以得到对应逆问题的上界。

此时对应的子问题模型变为:

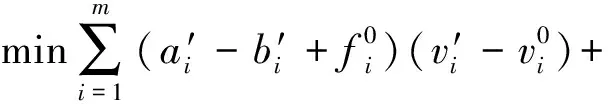
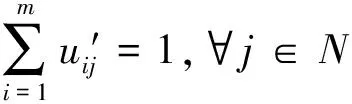
行生成算法及使用不同处理方法处理子问题求解的流程示意图如下:

图2 行生成算法及不同处理方法流程示意图

4 示例及计算结果

4.1 简单的例子

我们举一个简单的例子来具体展示无容量设施选址逆问题。

图3 原UFLP示例图

图4 给定可行解的IUFLP示例图

如上图所示，Ⅰ、Ⅱ、Ⅲ、Ⅳ为设施编号，每个设施开启成本为10。a,c,b,d为顾客编号，设施与顾客有连线表示该顾客可以被相应设施服务，连线上的数字表示对应的运输成本。黑色的细线表示该问题所有可行的服务连线，带箭头的粗线表示服务最优解连线。相应的设施开启成本和运输成本为:

图3中给出了在给定设施开启成本和运输成本后的最优解服务连线。图4则是给定了如图所示的服务连线，需要调整设施开启成本或运输成本使得该服务连线成为调整后最优的服务连线。

能够看出，原问题最优解如图3所示，即为开设设施Ⅱ服务顾客b，以及开设设施Ⅲ服务顾客a,c,d，对应的最优成本为27。而当给定可行解如图4所示时，即为开设设施Ⅲ服务顾客a,d，以及开设设施Ⅳ服务顾客b,c时，对应的成本为29。需要改变方框中的运输成本使得给定的可行解成为改变成本后的最优解，即将方框中1改为2，方框中2改为3。此时最小改变量为2，可以使得给定的可行解成为改变成本后问题的最优解。

4.2 计算结果

本文使用Windows 10操作系统，内存8 GB处理器为Intel Core i7- 8700的PC电脑上进行了所有的数值实验。所有算法均通过Matlab R2019a调用Gurobi求解器去实现。在数值实验中，我们对于6种不同规模随机生成了对应规模下20种可能的实例。(m,n)=(10,10),(10,20),(10,30),(20,20),(20,40),(30,30)。

其中设施启动成本和运输成本均为随机产生的整数值，且取值范围分别为：

fi=[100,200]；rij=[1,100],[100,200]

在实际中往往不能改变设施启动成本时，因而在接下来的计算中设置对于设施成本和运输成本调整量的权重分别为wf=∞,wr=1。

我们将采用下列方式来比较最优改变量和启发式算法计算得到的改变量之间的差距。当最优改变量不为0时，我们采用相对值(上下界改变量-最优改变量)/(最优改变量) 的方式来比较gap的大小。相应的结果见表1。由于给定的可行解是随机生成的，因而给定可行解刚好是最优解的可能性几乎为零。而当给定可行解刚好是最优解时，根据上述的算法可以知道不管是精确求解算法还是启发式算法，此时的最优改变量均为0。但在实际问题中，几乎不存在给定的可行解刚好是最优解，因为这样意味着不需要对原有成本做任何的改变，这里不再考虑这一极端情况。

结果如下:

表1 给定可行解非最优解时,IUFLP问题的计算结果

在表中，(m,n)-1表示IUFLP问题的规模。例如(20,40)-1表示20个设施和40个顾客：-1表示fi=[100,200],rij=[1,100];-2表示fi=[100,200],rij=[100,200]。

OS表示严格求解子问题时得到的逆问题的最优值。UB表示使用线性松弛的方法得到的 P的上界。LB表示使用邻域搜索得到的 P的下界。在表1中GAP计算方法为相对比值法。GAP1表示UB与OS之间的gap,GAP2表示LB与OS之间的gap。T1，T2，T3分别为得到最优值，上界，下界的计算耗时，单位为秒。表中所有的结果均是一个规模中产生的20个实例的平均值，并经过四舍五入处理。

特殊说明：在使用处理方法二得到下界的过程中，设置了最大循环次数1000。而在处理方法一和三中，设置的最大循环次数较大不会提前终止程序。

计算结果表明，问题的规模(m,n)以及设施开设成本fi与运输成本rij之间的大小关系不会对gap的大小造成太大影响。同时，由于该问题是NP-难的，随着规模的变大，计算复杂度和计算时间都是指数增长的。根据计算结果可以看出，线性松弛得到的上界与最优的改变量差距较小，但求解效率却没有较大提升。原因在于求解最优的改变量时是使用整数规划模型进行求解，而采用的求解器对于整数规划的求解效率较高；同时线性松弛方法在每次迭代循环过程中产生的是非整数解，迭代循环次数相对变多也增大了求解需要的时间。而利用基本的本地搜索方法求出的下界与最优的改变量非常接近，同时在求解效率上也有较大提升。因此，当问题规模不大时，可以采用最优解的方式进行求解；而当问题规模较大时，可以采用启发式方法结合一定的迭代循环次数得到不错的下界。迭代循环次数越多，计算耗时就越多，但得到的下界就越好。在实践中，针对具体的问题具体分析，使用启发式方法同时设置一定的迭代循环次数可以得到不错的成本改变量。

5 结论

本文针对无容量限制的设施选址逆问题进行了建模分析，提出了使用行生成算法将逆问题分为了主问题和子问题。通过对子问题中的整数规划模型进行求解可以得到逆问题的最优解。分析表明对于行生成算法中的子问题采用线性松弛法和本地搜索方法可以分别得到逆问题的上下界。数值实验结果表明了线性松弛法得到的上界与最优解较为接近，但求解效率并未有提升；启发式算法在下界的获取上则有着较为优异的表现，同时求解速度较快，说明了该启发式算法的有效性。

实际上，由于子问题是无容量限制设施选址的原问题，可以将求解该问题更为高效的近似算法用于其中，从而提高下界解的质量和求解效率。子问题是最具有优化空间的地方，可以结合启发式算法一次找出多个目标函数小于0的解，并一次性全部加入主问题中进行求解，从而提高求解效率。