考虑订单取件时间和柔性时间窗的取送货车辆路径问题
孙欣蕊, 李昆鹏, 刘腾博
(华中科技大学 管理学院,湖北 武汉 430074)
0 引言
近年来,同城配送市场不仅涌现一批新兴跑腿公司,而且传统快递企业、外卖企业纷纷扩展同城跑腿业务,从而同城跑腿配送已成为企业竞相争夺的蓝海市场。顺丰2019年同城业务营收19.52亿元,同比增长96.12%;2020年母亲节期间,UU跑腿当日订单量增幅50%以上。由于我国同城配送市场仍处于行业发展初期,各平台跑腿业务虽增速明显但配送模式尚未成熟。目前平台通常采用用户在平台下单,配送系统根据订单信息,将订单分配至骑手,待取件后平台自动生成预计到达时间再由骑手完成配送的模式。但因用户在下单时无法设置预期送达时间,导致订单完成时间多取决于骑手,存在很大不确定性,故此配送模式不适用于客户希望在指定时间内送达,骑手尽可能多地接收订单的实际场景。因此,基于此场景,如何科学的制定配送方案,进而提高配送效率、节约运力资源是需深入研究的重要课题。
本文所考虑的取送货配送模式:首先,用户在平台下单,每个订单信息包括任务起点和终点的具体位置、物品属性、取件时间限制及送达时间窗要求;然后,配送中心对一定时间内的客户订单,根据订单的取件时间要求及起终点位置为骑手派单并规划路线。在此配送模式下,为保障骑手权益,系统根据起终点位置之间的距离设定合理送达时间窗限制;为提升客户满意度,若骑手在送达时间窗外延迟或提前将物品送达,平台将根据偏离时间窗的程度采取一定惩罚,即用户预期送达时间窗为柔性时间窗约束且具有一定的惩罚成本,平台总惩罚成本越低说明配送准时率及客户满意度越高。基于此,本文以配送成本和惩罚成本之和最小为目标,研究具有订单取件时间和柔性时间窗约束的取送货车辆路径问题(PDVRPORDFTW)。
具有不同约束条件的取送货问题一直是研究热点,常见的约束条件包括:客户需求特点、车容量、车辆限制等。同时取送货车辆路径问题(VRPSPD)(马艳芳等[1]);需求可拆分的取送货问题(VRPSPD)(李寒梅[2]);带时间窗的取送货车问题(VRPTW)(祁文祥等[3],边展等[4])。本文考虑实际客户需求,研究具有订单取货时间和柔性时间窗约束的取送货车辆路径问题(PDVRPRDFTW),目前尚未有学者对具有两个客户时间约束的车辆路径问题进行探讨,相关研究多集中在带硬时间窗的取送货问题(PDPTW)以及带软时间窗的取送货问题(PDPSTW)。很多学者针对PDPTW提出精确算法和启发式算法进行求解。其中精确算法包括:分支-定价算法(Sun等[5];Ghilas等[6])。分支切割算法(Ropke等[7],Furtado等[8])。分支-切割-定价算法(Ropke等[9]),动态规划(Mahmoudi等[10]),基于集合分割的精确算法(Baldacci等[11])。相关启发式算法包括:禁忌搜索算法(Nanry等[12];Goeke[13]),自适应大邻域搜索算法(Ropke等[14]),模拟退火算法(Li等[15])。祁文祥等[3]对PDPSTW提出节约算法进行求解。分析发现,极少有学者对PDPSTW问题展开研究;对PDPTW问题的研究,集中在算法性能的优化及求解规模的提升。此外,已有文献在构造数学模型时多考虑车容、取货或送货的时间窗、访问优先级等约束,显然无法适用于客户对取货和送货时间均有要求的同城配送场景。基于此,本文在构建模型时将客户的取货和送货时间均考虑在内,并设计改进分支切割算法。相较于现有研究,更符合同城配送平台跑腿业务的实际需求,并且采用精确算法得到的最优解可以用来评价启发式算法的有效性,具有一定的指导作用。
本文的主要贡献包含:(1)构建了混合整数模型,并将非线性约束进行线性化转换;(2)根据问题的特性,考虑四种有效不等式,设计改进分支切割算法对模型进行求解;(3)根据实际数据构造算例,验证算法的有效性。
1 数学模型
1.1 问题描述及假设
本文所研究的问题描述如下:针对多个订单,配送企业进行订单分配和规划配送路线。已知信息包括:每个订单相应的起点和终点地址信息、订单需求量、每个订单对应的起点有相应的订单取件时间;每个订单对应的终点有相应的服务时间窗。客户对车辆的提早或延迟到达有一定的容忍度,因此考虑柔性的服务时间窗。目标是配送成本和惩罚成本之和最小。为了方便建模,考虑以下假设:(1)配送车辆数固定、车辆同质且匀速行驶、电量充足;(2)每个订单对应的需求量不超过车辆的装载能力;(3)每个订单由同一车辆进行配送;(4)车辆允许提前到达订单终点,但需在相应的时间限制内服务客户。(5)车辆服务客户的时间超出系统预计的时间窗,但未超出最晚到达时间时,有相应的惩罚。
1.2 符号说明
R:客户订单集合R={1,…,n};P={1,…,n}:订单起点集合,第i个订单对应第个起点;D={n+1,…,2n}:订单终点集合,第i个订单对应第n+i个终点;N=P∪D∪{0,2n+1}:节点集合,0和2n+1均表示配送站;A:弧的集合,A={(i,j)|i∈N,j∈N};V:车辆集V=={1,…,K};c:单位距离运输成本;C:单位时间延迟成本;T:车辆的最长工作时间;dij:从节点i到节点j的行驶距离;tij:车辆服务节点i的时间与从节点i到节点j的行驶时间之和;Q:车辆的最大运载量;ETi:订单起点i的最早可取件时间;(qi+qn+i):qi和qn+i分别表示订单起点i和终点n+i的配送量,qi=-qn+i≥0;[ETn+i,LTn+i]:订单终点n+i的预期送达时间窗;ELTn+i:订单终点n+i的最迟送达时间;xij:若车辆从节点i行驶至节点j,则为1;否则为0;Ai:车辆到达节点i的时间;Bi:车辆开始服务节点i的时间;Qi:车辆访问节点i后的车载量;vi:表示节i点的路径标志符号。
1.3 数学模型
1.3.1 模型建立
(28)
其中(1)为目标函数,使配送成本和惩罚成本之和最小。(2)表示有IN辆车从配送中心出发,执行配送任务,车辆访问的第一个节点是订单对应的起点。(3)~(4)表示每个节点被访问一次,并保证流平衡。(5)保证所有车辆配送访问的最后一个节点是配送站。(6)~(7)表示车辆访问节点后,车辆装载量的限制。(8)保证车辆装载量的一致性。(9)表示车辆到达节点后才开始服务。(10)保证车辆连续先后访问节点i和节点时,Bj≥Bi+tij。(11)表示一个订单只能由一辆车配送,并且车辆需先到订单对应的起点取货,再配送至订单对应的终点。(12)~(13)保证当车辆先后连续访问两个节点i和j后,Aj=Bi+tij。(14)表示当车辆到达订单对应起点的时间小于等于它对应订单取件时间,则需在订单取件时间取货。(15)表示当车辆提前到达订单对应终点,需要等待,直到订单对应终点预期的最早服务时间点,才进行服务。(16)表示车辆需在订单对应终点可承受的最晚送达时间点前服务。(17)表示当配送服务顾客的时间点超过预期时间窗,但不超过最迟服务时间点时,有一定的惩罚。(18)~(23)表明同一车辆访问的所有节点的路径标志符号相同,且路径标志符号等于该车辆访问的第一个节点序号。(18)规定了所有节点的路径标志号的取值范围。(19)~(20)保证当车辆离开配送站后访问的第一个节点为时,节点i的路径标识符号为i。(21)保证单个订单的取货点和送货点由同一车辆进行访问。(22)~(23)表示如果车辆连续访问节点i和j时,则节点i和j的路径标识符是相同的。(24)~(28)是定义的变量取值限制。
1.3.2 模型的线性化
由于约束(14)、(15)、(17)是非线性化形式,因此上述模型是非线性的。为降低模型求解的复杂度,将(14)(15)(17)转化为线性形式。
为使(14)-(15)线性化,定义0-1变量,u0i,∀i∈P并用以下约束(29)~(34)代替:
Bi≥Ai,∀i∈P∪D
(29)
Bi≤Ai+T(1-u0i),∀i∈P∪D
(30)
Bi≥ETi,∀i∈P∪D
(31)
Bi≤ETi+Tu0i,∀i∈P∪D
(32)
Ai≥ETi-T(1-u0i),∀i∈P∪D
(33)
Ai≤ETi+Tu0i,∀i∈P∪D
(34)
为线性化(17),定义变量wn+i,0,wn+i,1,wn+i,2,zn+i,0,zn+i,1并用(35)~(43)代替:
wn+i,0,wn+i,1,wn+i,2≥0,∀n+i∈D
(35)
zn+i,0,zn+i,1∈{0,1},∀n+i∈D
(36)
wn+i,0+wn+i,1+wn+i,2=1,∀n+i∈D
(37)
zn+i,0+zn+i,1=1,∀n+i∈D
(38)
wn+i,0≤zn+i,0,∀n+i∈D
(39)
wn+i,1≤zn+i,0+zn+i,1,∀n+i∈D
(40)
wn+i,2≤zn+i,1,∀n+i∈D
(41)
Bn+i=ETn+iwn+i,0+LTn+iwn+i,1+ELTn+iwn+i,2,∀n+i∈D
(42)
P(Bn+i)=C(ELTn+i-LTn+i)wn+i,2
(43)
从而为使目标(1)线性化,考虑
(44)
因此,混合整数线性模型为(44),(2)~(13),(16),(18)~(43)。在下述部分中是考虑该线性模型。
2 有效不等式
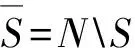
2.1 车容量不等式
对于AS⊂P∪D,k(S)表示服务集合S所需车辆数的下界。在任意可行解中,服务S中所有节点的车辆数大于等于k(S),其中,k(S)可取值为max{1,「q(π(S)S)/Q⎤,「-q(σ(S)S)/Q⎤}[9],则可表示为:
(45)
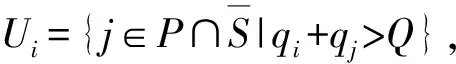
(46)
2.2 优先顺序不等式
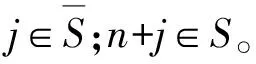
(47)
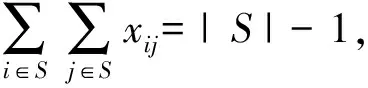
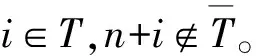
(48)
2.3 加强子回路移除不等式
考虑集合S⊂P∪D,则任意一个可行解满足以下不等式:
(49)
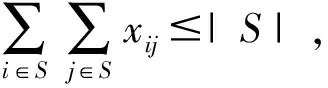
基于S,考虑∀p∈ρ(S),∀n+q∈γ(S),则式(49)可提升为下述有效不等式:
(50)
2.4 路径不可行不等式
命题1W=(n+i,j,n+k)表示包含三个节点的路径,其中n+i,n+k∈D,j∈P。令W1=(i,k,n+i,j,n+k,n+j),W2=(k,i,n+i,j,n+k,n+j)。若W1和W2均不可行,则路径W不包含在任意可行解中。
证明假设W存在一个可行解中,因车辆配送满足优先约束,则节点i和节点k在W之前被访问,节点n+j在W之后被访问。然而,与假设条件矛盾,因此W不包含在任意可行解中。
命题2对于节点i∈P,有qi+qj>Q,∀j∈P{i}。令R={0,j,n+j,i},其中i,j∈P,n+j∈D。如果对任意j∈P,R不可行,则节点i是车辆离开节点0后访问的第一个节点。
证明假设节点i不是车辆离开节点0后访问的第一个节点,且对于任意节点j∈P{i},有qi+qj>Q,从而节点h∈P{i}和n+h∈D满足0→h→n+h→i。然而,与假设条件矛盾,因此节点i是车辆离开节点0后访问的第一个节点。
综上,则下述不等式有效:
xn+i,j+xj,n+k≤1,W1,W2不可行
(51)
x0i=1,R不可行
(52)
3 改进分支切割算法
3.1 预处理
若任意可行路径不包含弧(i,j)∈A,则称(i,j)是冗余的。因此,为避免出现冗余的情况,通过在数学模型中加入以下约束,加快求解速度。
(1)对于满足条件ETn+i>ELTn+i的送货点,有n+i,n+j∈D,有xn+i,n+j=0。
(2)如果P=(j,i,n+j,n+i)为不可行路线,则弧(i,n+j)是冗余的,从而xi,n+j=0;同理,如果P=(i,n+i,j,n+j)为不可行路线,则弧(n+i,j)是冗余的,从而xn+i,j=0。
(3)2.4部分的路径不可行不等式(51),(52)。
3.2 分离算法
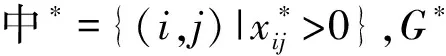
3.2.1 分离车容量不等式
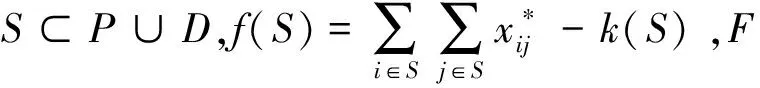
3.2.2 分离优先不等式
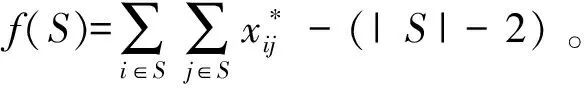
3.2.3 分离子回路移除不等式
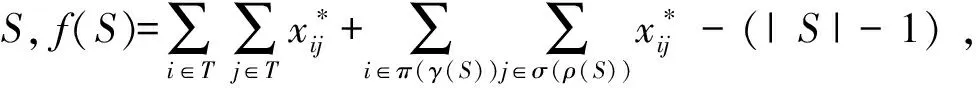
3.3 改进分支切割算法求解步骤
步骤1初始化:令Φ表示活跃节点的集合,当前活跃节点t为根节点0,将其添加到Φ;zbest为目标最优解,zbest←+∞。
步骤2预处理:根据3.1部分的预处理,删除图G中冗余的弧,从而减少求解规模。
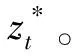
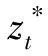
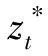
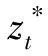
步骤7节点选择:若Φ是空集,则算法停止;若Φ不是空集,则根据下界优先策略选择一个节点t进行求解,令Φ←Φ{t},并转到步骤4。
步骤8分支:从{xij|∀i,j∈N}中选取一个对应的解是小数解的变量进行分支,生成两个子节点,并添加到Φ。
4 数值实验
4.1 算例构造
根据某平台的订单数据,提取预约模式下某时段内的订单数据。利用百度拾取坐标系统,计算任意两个节点之间的距离。在此基础上构造5组不同订单规模的算例进行测试{10,20,30,40,50},每种规模随机生成5个算例,共25个算例,各项实验参数如下:车辆装载能力Q=7;车辆最长工作时间T=60;单位配送成本c=0.2;单位时间延迟成本C=0.2;任意两节点间的行驶时间tij=dij/speed(speed=21km/h);客户节点的时间窗长度W=25;对每个订单(i,n+i),对应的需求量qi~U[1,7],qn+i=-qi,ri~U[5,10],ETn+i=ri+ti,n+i,LTn+i=ETn+i+W;ELTn+i=LTn+i+5,qi~U[1,7]。
4.2 有效不等式性能分析
为分析提出的有效不等式对模型的改进效果,考虑在搜索树的根节点处添加不同的有效不等式,并比较它们对下界的影响。表1表示不同的不等式添加策略下的下界值。第1列为算例名称(例如10_1,10个节点规模下第1个算例);第2列为只求解模型得到的下界值;Prece、Subtour、Cap分别表示优先顺序不等式,加强子回路移除不等式和车容量不等式。第3~8列是在搜索树的根节点处添加对应的不等式的下界值。
结果表明,对于8种处理方式下的平均下界,在搜索树的根节点处,相比于只求解模型,7种处理方式均能不同程度的提高搜索树根节点的下界;同时考虑3种有效不等式具有最好的平均下界。此外,相比于优先顺序不等式和加强子回路不等式,车容量不等式的效果最好;在搜索树的根节点处,相比于考虑一种不等式或两种不等式的添加策略,同时考虑三种不等式是最好的不等式添加策略。因此,在改进分支切割算法中,将同时考虑三种不等式作为添加策略。
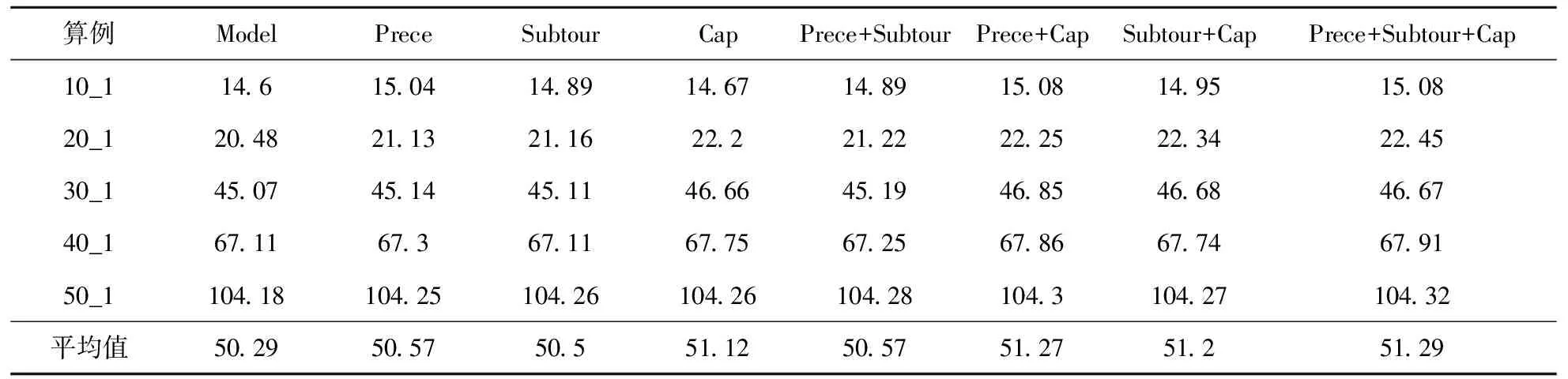
表1 有效不等式的结果比较
4.3 改进分支切割算法与CPLEX默认的分支切割算法的比较
为验证改进分支切割算法的效果,将其与CPLEX默认的分支切割算法进行比较。表2表示时间限制为1h下两种算法求解的结果。其中第1列与表1中的第一列有相同的含义。统计两种算法下每个算例的下界,运行时间,Gap。Gap=100%(第5列值-第3列值)/第3列值,“*”表示该算例求得最优解。
由表2可知,(1)对于两种算法获得最优解的个数, 25个算例中,改进分支切割算法能够获得25个算例的最优解;CPLEX默认的分支切割算法只能够获得6个算例的最优解。(2)对于两种算法在1h的运行时间内获得的平均下界,改进分支切割算法的平均下界为50.94,CPLEX默认的分支切割算法的平均下界为38.08,故相比于CPLEX默认的分支切割算法,改进分支切割算法使平均下界提高33.8%。(3)对于不同规模的算例,两种算法对规模为10,20,30,40,50的算例,改进分支切割算法分别求得5,5,5,5,5个算例的最优解; CPLEX默认的分支切割算法分别求得5,1,0,0,0个最优解。综上,算例规模较小时,改进分支切割算法求解时间短,有实用性;随着规模的增加改进分支切割算法可以在较短时间内求得最优解;并可代替CPLEX,提供更好的下界,评估相关问题的启发方法的性能。
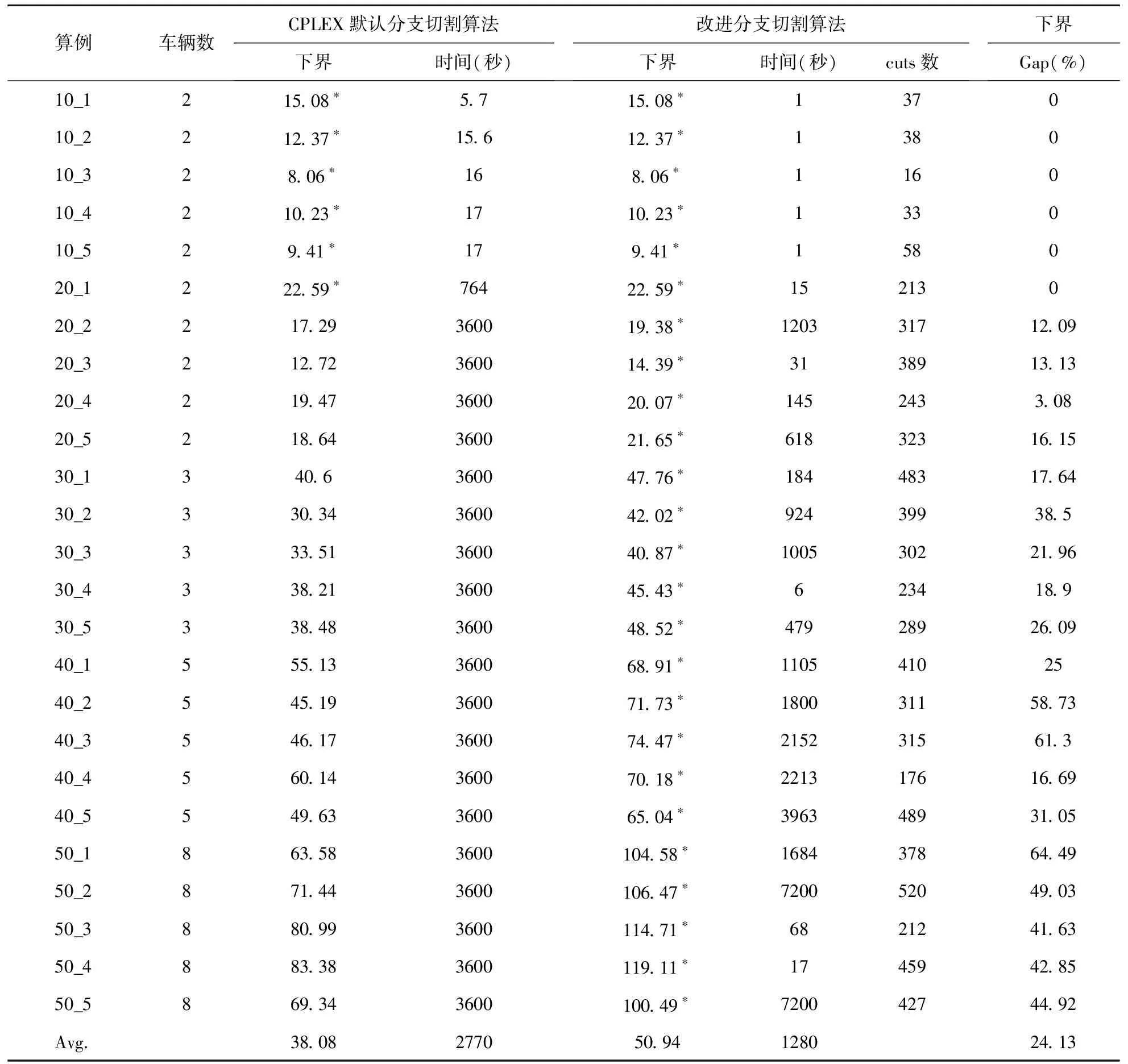
表2 改进分支切割算法与CPLEX默认分支切割算法的结果比较
4.4 参数对成本的影响分析
为分析车辆数,车辆装载能力不同水平对成本是否有影响,针对单个算例30_1,考虑车辆数三种水平(nv=3,4,5),车辆装载能力四种水平(Q=7,8,9,10),构造12个算例。对所有算例,采用改进分支切割算法,求得最优解,结果如下图所示。
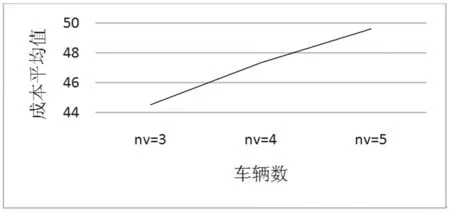
图1 不同车辆数下平均成本折线图
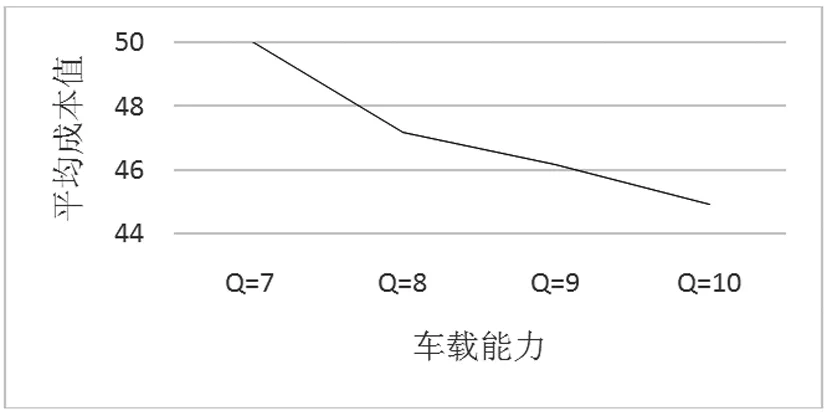
图2 不同装载能力下平均成本折线图
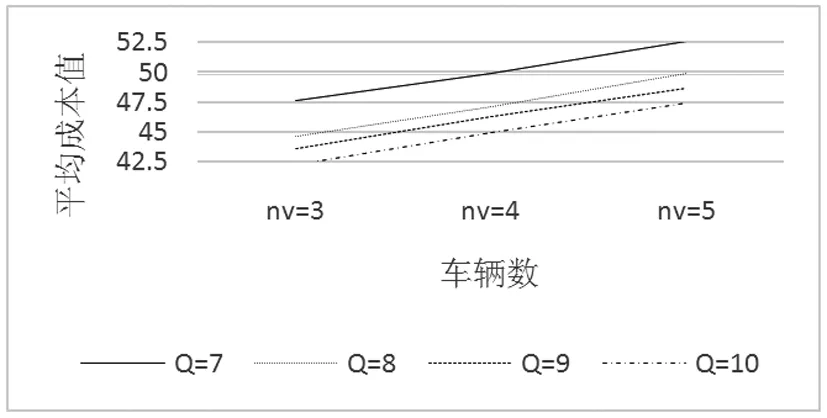
图3 车载能力与车辆数交互作用下成本折线图
结果表明,(1)对于不同车辆数下的成本,则有成本随着车辆数的增多而增大(图1所示);(2)对于不同车载能力下的成本,则有成本随着车辆装载能力的增大而减少(图2所示)(3)对于车辆装载能力与车辆数交互作用下的成本,在不同的车辆数水平中,各个车辆装载能力下的成本按照相同的规律变动,则有车辆装载能力和车辆数不存在交互作用(图3所示)。综上所述,车辆数和车辆装载能力不仅对成本有显著影响,而且车辆数越少,车辆装载能力越大,成本越少。
5 结论
本文研究了考虑订单取件时间和柔性时间窗的取送货车辆路径问题,并使配送成本和超时惩罚成本之和最小。首先,提出混合整数线性模型;根据该问题的特性,提出四种有效不等式;设计改进的分支切割算法。其次,通过数值算例,比较每种有效不等式的有效性,结果显示每种不等式能够不同程度的提高模型下界;最后,在有限的运行时间内,与CPLEX的分支切割策略相比,验证算法的有效性。本文不仅可以丰富车辆路径问题文献,还为评价城市物流平台设计的启发调度算法性能提供参考。此外,适当的减少车辆数,适当的增加车辆装载能力,可有效的降低成本。
本文考虑了有确定性因素的带时间窗的取送货问题,而随着订单的需求个性化的不断增加,未来研究可以考虑订单分配和路径规划中的不确定因素。

