“理解为先”模式下初中数学大单元教学设计的思考与应用

庄 河

(泉州第十六中学，福建 泉州 362100)

0 引言

“理解为先”(Uderstanding by Design)教学模式，亦称“UbD逆向设计”教学模式，是由当代美国教学改革专家格兰特·威金斯和杰伊·麦可泰格开发而得.他们将具有多维性和复杂性的“理解”概括界定为6个侧面，对教与学的设计具有关键性的指导意义，受到美国课程开发学会(ASCD)的关注，并进行试验推广，值得一线教师在课堂教学中进行研究和实践．

“理解为先”的教学模式认为：教师在考虑如何开展教学活动之前，先要努力思考学生的学习要达到什么目标？能用什么方式或评估证据表明学生已经达成这些学习目标？因此，要求教师在确定了所追求的教学结果后，通过教学的预期结果提炼教学中基于核心素养的“大概念”，据此设计教学“核心问题”，从而进一步考虑评估方案，最后才是设计教学活动．它是一种目的性更强、更为细致的思维方式和教学设计方式，为教师提供了一个概念性强的框架以及附带的一套设计标准，能使学生更容易理解课程的内容，并达到预期目标．

1 “理解为先”教学模式的思考与应用

“理解为先”教学模式的主要目的是发展学生的深层学习，以解释、阐明、应用、洞察、神入(或移情)、自知作为“理解”由浅入深的6个衡量标准(也称为“理解”的6个侧面)[1]．

“解释”是指恰如其分地运用理论和图示，有见地、合理地说明事件、行为和观点；“阐明”是指演绎、解说和转述，从而提供某种意义；“应用”是指在新的、不同的、现实的情景中有效地使用知识；“洞察”是指批判的、富有洞见的观点；“神入(或移情)”是指感受别人的情感和世界观的能力；“自知”是指知道自己无知的智慧，知道自己的思维模式与行动方式是如何促进或妨碍了认知[2]．

在这6个衡量指标中，“解释”通常是其他5个指标必须包括的内容.在“理解为先”教学模式的表现性评估中，需要在清晰的推理和阐述之下，先对任务和表现进行反思、评估和调整；再根据学习目标，以结果为导向，确定核心问题，以这样逆向思考的方式设计教学，在教学的初始环节优先利用核心问题或问题链来明确预期的学习结果，指向理解及核心素养；接着选择并确定合适的教学行为(评估证据)，确定可接受并能用以评估学生是否达到学习目标的证据，以及对学生进行形成性评价；最后规划相应的学习体验和教学活动，达到有效学习并实现学习目标，使得教师教得更加高效、精准，学生学得更加有效、透彻(具体步骤如表1所示)．

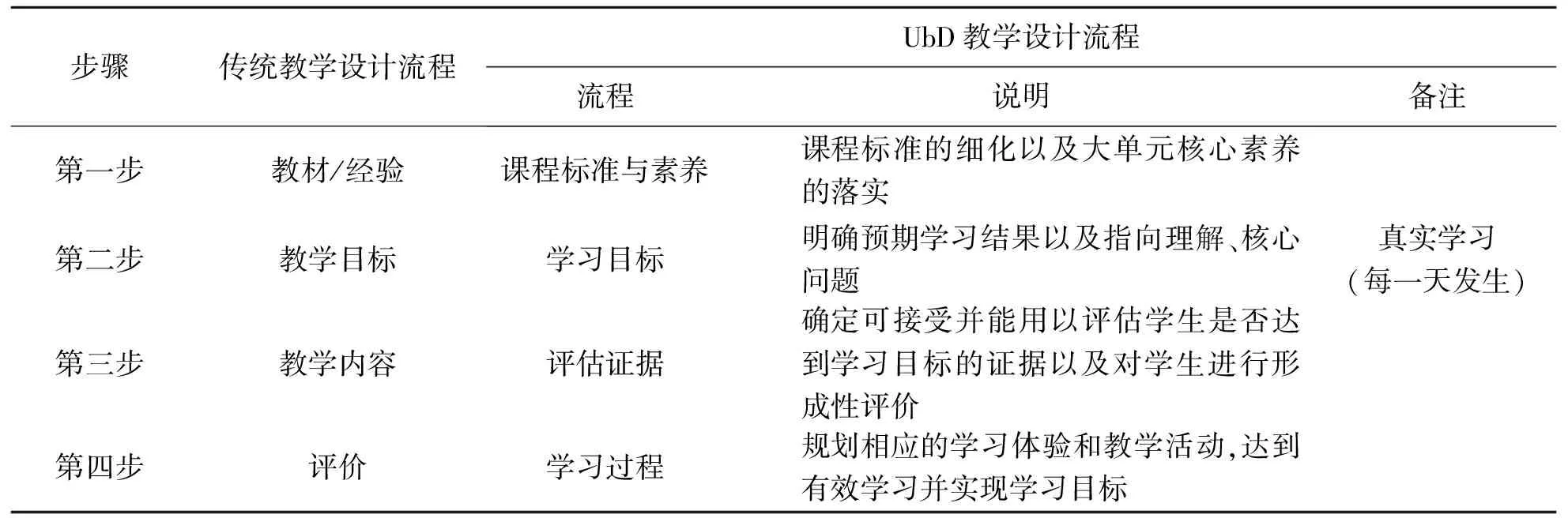
表1 UbD教学设计流程与传统教学设计流程对比表

“理解为先”教学模式的主要目的是发展和深化学生的理解.该模式要求教师从预期的教学结果出发，开展从“预期结果—评估证据—教学设计与学习规划”的3阶段教学设计，以防止盲目的精细化教学规划．

第一阶段：评价前置，同时关注基于课程标准、核心素养产生的预期结果与确定目标;

第二阶段：结合评估证据以及表现型任务，判断学生是否达到了预期的目标和理解;

第三阶段：形成具体的学习计划与内容,把握学生的学习情况,提炼教学内容和知识点．

整体规划先于教学是重要的，让学生理解并掌握核心概念与学科关键能力点是教学中不可或缺的．教师应该把理解6个侧面渗透到逆向设计的3个阶段,因为它们能帮助教师弄清所需的理解、必要的评估任务和最有可能促进学生理解的学习活动．这6个侧面提醒教师:理解不是简单地依靠陈述事实,为了让学生能获得所期望的结果,理解需要有一定的学习行动和相应的评估方案及评估工具．

2 关于“理解为先”教学模式的设计分解

2.1 关于“阶段1：预期结果”的理解与相关案例

案例1UbD设计模板之“分式的运算”.

学习迁移1)学习分式的运算有利于概括出初中“数与代数”体系运算的一般步骤；

2)通过类比分数的学习过程，在探究分式的概念、性质和运算法则的形成过程中，体会数式通性以及“从具体到抽象，从特殊到一般”的化归思想方法，发展合情推理能力．

意义建构基于UbD设计模板的需要，笔者将“分式的运算”的意义建构分为“深入持久的理解(即学生将理解的是……)”和“核心问题(即能够促进探究、理解和学习迁移……)”两个部分．其中“深入持久的理解”分为以下3点：1)分式的基本性质是分式恒等变形的依据，也是进行分式四则运算的理论基础；2)分式的运算分步骤，即明确算式结构、运算顺序、运算法则、最优算法、书写步骤、求得运算结果；3)类比、化归、整体带入的思想方法的应用．与之相应的“核心问题”也可分为3点：分式的基本性质有什么作用？分式运算的一般流程是什么？在研究分式运算过程中用到了哪些思想方法？

在阶段1制定统一的单元规划前提下，可以确保规划与设计的一致性．单元目标若能较好地达成，则有助于减少练习与作业的数量，对作业进行优化，有利于落实“双减”政策和“五项管理”规定．阶段1“预期结果”的设计需根据《义务教育数学课程标准(2022年版)》(以下简称《新课标》)中的知识逻辑进行编制，明确学习内容的优先次序，突出引导性、清晰的总括性目标，以此进一步细化教师与学生需达成的学习目标，通过明确次序的优先级别，建构学习与体验．如果教学设计中没有清晰的目的和明确“表现性”的目标，那么将导致学生在课堂中难以呈现出令人满意的结果．

2.2 关于“阶段2：明确评估证据与核心任务”的理解与相关案例

案例2关于“有理数的乘法1”一课的作业设计.

学习目标1)能借助实际情景，理解并记忆有理数的乘法法则；

2)会根据有理数乘法运算法则，正确熟练地进行有理数乘法运算；

3)理解倒数的概念，会计算已知数的倒数．

( )

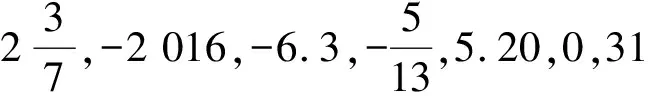
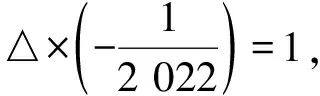
阶段2“明确评估证据与核心任务”环节中，可根据初中数学学科的特点精选例题与练习，同时研发校本作业、例题与《新课标》抑或是“关键教学点”的对应关系.针对学生的每一道错题倒推知识点的缺漏，这样可以更好地明确“评估证据”，从而精细教学诊断．

案例3UbD单元设计之“有理数的运算”(核心任务：学生评价量规，见表2).

表2 学生评价量规

由表2可知：有效的“评估证据”不应局限于例题，可以通过“量规”进行评估.这样的量规能有效列出标准的等级，在指导教师教学活动的同时，也为学生课堂学习活动提供量化评价标准.这样不仅关注学习结果，同样关注学习过程，有利于引导学生向既定的教学目标(学习目标)努力．

“理解为先”模式中“阶段3：学习活动的设计”这一环节，关于“教学活动设计”，教师需针对具体的教学内容进行拓展，与传统教学设计一样，一般包括教学内容、教学过程、板书设计、作业设计、时间分配等环节，本文不再赘述．

3 “理解为先”模式下核心问题的确定与预期结果的达成

3.1 对于“核心问题”的理解

教学设计的目标是让学生充分感知所学知识并灵活运用，因此设计中必须关注链接所有离散知识和技能，并为它们带来意义的“大概念”[3].在数学教学中需以核心问题为架构，唯有如此才能有效组织零散的知识点，并将其塑造成吸引学生、引发深思、有效的教学方案．

如何确立核心问题？大单元教学设计以目标为导向，在确定核心问题前，需制定贯穿整个大单元教学环节的最终目标(阶段1)，这一点非常重要．数学的学习应利用核心问题引导学生依据核心概念与重要观点进行思考，而非对重要观点进行无效的组织．

3.2 核心问题的特征

何为核心问题？核心问题首先是能引起学生不断思考与共鸣甚至于激发兴趣，能促进学生对问题产生疑问，并主动探究学习、理解意义，产生适度的学习迁移.核心问题的引入能促进学生形成技能．

关于如何编制核心问题，我们采用“理解为先”教学模式开发者的引例，或许能更为直白地说明问题：

“三角形全等”单元教学中的核心问题有两个：1)要让两个三角形全等，除了6个元素中的3条对应边都相等、3个对应角都相等之外，应提前让学生预判或准备什么，才能将三角形全等的6个已知元素尽可能性地降低；2)要使得三角形全等，这两个三角形应该具备什么样的条件(或相等元素)．

显而易见，这样的问题能促进学生在学习三角形全等的过程中不断思考，同时让学生明白三角形全等并不需要6个元素齐全，而在于能否通过其中3个已知元素来判断三角形的“唯一性”，直达“三角形全等”单元教学的核心.这更简单地说明核心问题的特征及重要性．

3.3 核心问题与教学重点的区别

核心问题不同于教学设计中的教学重点,主要体现在以下3点：1)跨度不同，核心问题针对大单元教学，而教学重点是针对单一课时而言；2)对象不同，核心问题往往是学生学习中应思考的，而教学重点常常指教学的侧重点；3)顺序不同，核心问题应在大单元教学之初进行设计，而教学重点常在单一课时备课中思考．核心问题的掌握亦可作为学生学习的评估证据，而教学重点常作为授课有效性的依据．

核心问题涉及两个方面：理解与运用．这样的核心问题需学生灵活运用先前的知识并主动进行“理解”建构，这个过程促进学生提出并尝试解答关键性问题，得出推论，产生理解，自觉应对迁移后的应用．教学不仅是教授，还在于回答并满足学生的需求，大单元的核心问题足以证明这一教学目标．

3.4 初中数学核心问题的设计

如在“一次方程(组)、不等式(组)”大单元教学中，用字母表示数是学习本单元的基础，而等式与不等式的性质是解方程与解不等式的概念依据.为引导学生由具体思维向抽象知识进行转换，可以设计如下核心问题：1)如何运用数学符号化语言(代数式)转化实际问题的未知量(用字母表示数、设未知数)；2)现实中的未知量如何解出，需要什么样的条件或是关系(找寻等量关系与不等关系)；3)有什么样的方法可以解决你用符号语言列出的关系(等式与不等式性质，解方程与不等式的步骤与方法及其共同点)．

再如“一元二次方程与二次函数”大单元教学中，学生可以联系一次函数与一次方程之间的关系，以此为铺垫，进一步突出函数方程模型在实际生活中的应用价值，可做如下核心问题设计：

1)以前我们从一次函数的角度看一元一次方程，认识了一次函数与一元一次方程、不等式的联系，当次数变为2时，情况会怎样呢？

2)如何求解一元二次方程中的未知数呢？当该一元二次方程变成二次函数时，此时二次函数的图像性质如何推导呢？能否在已经学习的知识中寻求答案(利用完全平方公式得出配方法、描点法与逐一增加参数得出图像性质)？

3)类比一次方程与函数、二次方程与函数在生活中如何运用，能解决什么样的现实问题(即在数学建模、函数与方程方面的应用)？

4 后记

在培养核心素养的目标下，整合教材内容、实施单元教学并进行大单元整体设计能有效扩展学生的学习时间与空间.在具体实施中,应关注教学理论、观点、能力的落实．利用UbD教学设计模式对教材内容进行大单元式的有机整合，能让学生有更多的机会去参与、思考和实践，同时让学生更加主动地参与解决数学问题的过程，培养自己的数学思维能力，促进自身数学核心素养的形成与提升．