基于尺度优化形态学滤波的滚动轴承故障诊断

王圣博，陈丙炎，程尧，梅桂明

(1.西南交通大学，成都 610031；2.牵引动力国家重点实验室，成都 610031)

从设备运行状态监测信号中提取故障相关的冲击特征是旋转机械故障诊断的关键。滚动轴承在现代旋转机械设备中广泛用于支承轴的高速旋转，由于复杂的工作环境和恶劣的工作条件而极易产生故障[1]，因此滚动轴承一直是旋转机械故障诊断领域的重点研究对象。由于滚动轴承运行工况复杂，采集到的振动信号受到各种噪声和信号调制干扰的影响，如何有效消除背景噪声并从复杂的监测信号中提取故障特征成为滚动轴承故障诊断的难点[2]。

形态学滤波是一种非线性信号处理技术，具有原理简单，计算高效，消噪性能良好的优势，近年来在旋转机械故障诊断领域得到了广泛应用。文献[3]采用开闭-闭开组合形态滤波器对振动信号进行降噪；文献[4]构造了组合形态学帽变换算子，通过频响特性分析考察算子的滤波性质；文献[5]利用4种基本形态学算子构造了3种性能增强的形态学算子，并采用Teager能量峭度作为加权指标提出了一种自适应加权多尺度组合形态滤波方法；文献[6]采用平均组合算子(Average Operator，AVG)提取滚动轴承振动信号中的冲击成分，用信噪比作为指标筛选最优结构元素长度：上述方法能够提取信号中的正负故障冲击特征并实现弱背景噪声干扰下的滚动轴承故障诊断，但在强背景噪声干扰下的效果不佳。文献[7]引入形态学梯度算子(Morphological Gradient，MG)用于轴承振动信号中正、负故障冲击特征的提取，以单个周期内的谐波波形为基础构造新的结构元素；但所构造的结构元素长度区间过大，计算效率不高，不利于在线应用。文献[8]提出了基于信号局部峰值的自适应多尺度形态学分析方法，根据信号局部峰值点自适应确定结构元素长度区间，但由于信号峰值易被随机噪声干扰且所得信号峰值并不准确，构造的结构元素长度区间较小，导致滤波信号中仍存在过多的残余噪声。

在上述分析基础上，本文基于文献[5]提出的三种形态学算子构造了改进形态学帽乘积算子(Improved Morphological Hat Product Operator，IMHPO)，用于增强轴承振动信号中的故障冲击特征；此外，提出一种新的基于信号极小值点确定结构元素长度区间的方法，以形态滤波信号的Hoyer测度(Hoyer Measure，HM)[9]为评估指标筛选最优结构元素长度，实现对故障冲击特征的准确提取；最后采用对角切片谱(Diagonal Slice Spectrum，DSS)对形态滤波信号进行增强以消除宽带噪声和进一步凸显故障冲击特征，并通过仿真和试验分析验证该方法在强噪声干扰下提取轴承故障特征的有效性。

1 理论基础

1.1 形态学乘积算子

数学形态学的基本思想是通过构造一个称为结构元素的滤波窗，对采集到的振动信号进行匹配分析，以达到滤除噪声和提取瞬态冲击特征的目的。设振动信号f(n)和结构元素g(n)分别为定义在F=(0,1,…,N-1)，G=(0,1,…,M-1)上的离散函数，N和M分别为信号和结构元素的长度，且N≥M，则f(n)关于g(n)的腐蚀、膨胀、开、闭算子分别定义为

(fΘg)(n)=min[f(n+m)-g(m)]，

(1)

(f⊕g)(n)=max[f(n-m)+g(m)]，

(2)

(f∘g)(n)=(fΘg⊕g)(n)，

(3)

(f·g)(n)=(f⊕gΘg)(n)。

(4)

这4种基本形态算子具有低通滤波的特点，单一使用时会一并滤除振动信号中的高频噪声和故障冲击信息，难以有效提取故障冲击特征；组合不同的基本形态学算子则可以有效提取振动信号中的重复冲击特征，且滤波效果优于单一形态学算子[4]，常用的组合形态学算子见表1。

表1 常用于冲击特征提取的组合形态学算子

由于振动信号中的故障冲击特征易被背景噪声干扰，为了增强振动信号中的冲击特征，文献[12]提出了一种形态学梯度乘积算子(Morphology Gradient Product Operator，MGPO)，文献[13]提出了一种形态学帽乘积算子(Morphology Hat Product Operator，MHPO)，定义分别为

OMGPO(n)=GC&O(n)GCO&OC(n)，

(5)

OMHPO(n)=OAVGH(n)OCMFH(n)。

(6)

文献[5]基于4种基本算子构造了3种性能增强的基本形态学算子来进一步增强形态学算子的滤波效果，其分别为闭-膨胀-腐蚀算子(Closing-Dilation-Erosion，CDE)

FCDE(n)=(f·g⊕gΘg)(n)，

(7)

腐蚀-开-膨胀算子(Erosion-Opening-Dilation，EOD)

FEOD(n)=(fΘg∘g⊕g)(n)，

(8)

开-腐蚀-膨胀算子(Opening-Erosion-Dilation，OED)

FOED(n)=(f∘gΘg⊕g)(n)。

(9)

为提取振动信号中的正负故障冲击特征，本文基于上述3种性能增强的基本形态学算子构造了2种新的形态学平均帽算子，其定义分别为

(10)

(11)

并基于形态学帽乘积算子对故障冲击特征的增强特性，进一步提出了一种改进形态学帽乘积算子用于增强轴承正、负故障冲击特征，即

FIMHPO(n)=

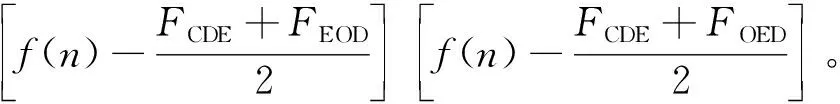
(12)

1.2 结构元素的长度范围

结构元素包括形状、幅值和长度三要素。研究表明，结构元素的形状和幅值对滤波结果影响较小。为提高计算效率，本文选择高度为0的扁平型结构元素[14]。

结构元素长度参数的合理选择对滤波结果有重要影响，通常根据采样频率与故障特征频率的比值确定形态学滤波的最大结构元素长度，但计算效率偏低且较难实现在线应用。本文提出一种新的结构元素长度范围确定策略，该策略完全依赖于振动信号的固有特性，无需待分析信号的先验知识，具体实现步骤如下：

1)识别振动信号中的所有极小值点的位置p=[p1,p2,…,pJ]，其中pj为第j个极小值点的位置，J为极小值点的数量。

2)根据各个极小值点的位置得到相邻2个极小值点的间隔L=[l1,l2,…,lJ-1]，其中

lj=pj+1-pj+1；j=1,2,…,J-1。

(13)

3)根据最小间隔和最大间隔确定结构元素的长度区间[Lmin,Lmax]，即

Lmin=min(L)，

(14)

Lmax=ηmax(L)。

(15)

考虑到信号的极值点易被随机噪声干扰，所得信号极小值点并不准确，遂给予结构元素长度范围一个系数η(η取3～5之间的整数,本文取3)[15]。

1.3 对角切片谱

由于采集到的原始信号中包含强烈的背景噪声，形态学滤波后的信号中仍含有一定数量的残余噪声，这将对故障特征提取造成一定的干扰。三阶累计量对角切片(Third-Order Cumulant Diagonal Slice，TOCDS)能有效消除振动信号中的背景噪声，突出周期性成分，其频谱即对角切片谱能检测到二次频率耦合。因此，本文采用对角切片谱对形态学滤波信号进行处理以消除故障无关分量，凸显故障特征。此外，为满足三阶累计量对角切片的计算条件，计算前对形态学滤波信号进行了去均值处理。

设x(t)为零均值实数平稳离散时间信号，其三阶累积量定义为

C3x(τ1,τ2)=E{x(t)x(t+τ1)x(t+τ2)}，

(16)

三阶累计量对角切片为τ1=τ2=τ时从二维矩阵C3x(τ1,τ2)获得的一维序列，定义为

C3x(τ)=E{x(t)x(t+τ)x(t+τ)}，

(17)

对角切片谱定义为三阶累计量对角切片的傅里叶变换，本质上等效于双谱中沿着次对角线的一条直线[16]，可表示为

(18)

式中：E{·}为期望运算；τ1，τ2为时移。

2 IMHPO-DSS方法

结构元素的长度对滤波效果有重要影响，元素长度过短会忽视对全局信息的把握，达不到去除无用信息的目的，过长则会导致有用信息的损失。为选择最优的结构元素长度，采用Hoyer测度设置评价指标MHM，其对轴承故障相关的重复冲击具有较高的敏感性，且对于随机冲击的鲁棒性强于峭度和负熵，可用于评估信号中的重复冲击特征，因此将MHM最大的滤波信号对应的结构元素长度作为最优结构元素长度。

(19)

式中：y(n)为滤波后的信号；N为信号长度。

综上所述，基于改进形态学帽乘积算子和结构元素选择策略，结合对角切片谱以及评价指标MHM，提出了一种轴承故障特征提取的IMHPO-DSS方法，其具体实现步骤如下：

1)采集滚动轴承振动加速度信号。

2)根据采集的振动信号和提出的结构元素长度范围确定策略确定结构元素的长度区间。

3)采用改进形态学帽乘积算子和确定的结构元素长度区间对振动信号进行多尺度形态学滤波。

4)将形态学滤波信号的MHM作为衡量各结构元素长度下轴承故障特征提取效果的指标，选取具有最大MHM的形态学滤波结果作为最优的滤波结果。

5)计算最优形态学滤波结果的对角切片谱以突出故障相关特征。

6)对对角切片谱进行分析，并根据轴承故障特征频率诊断轴承故障。

3 仿真分析

3.1 轴承故障信号仿真模型

利用滚动轴承内圈故障仿真模型[16]验证IMHPO-DSS方法的有效性。仿真信号x(t)=x1(t)+x2(t)+x3(t)+n(t)，其中x1(t)为周期性故障冲击，x2(t)为离散谐波，x3(t)为随机干扰冲击，n(t)为背景噪声。

(20)

(21)

(22)

式中：M为故障冲击特征数量；T为冲击周期；Ai为仿真信号的调制幅值，Ai=0.5[1-cos(2πfrt)]；fr为轴承内圈转动频率；fa，φa和Da分别为故障冲击引起的共振频率、相位和共振衰减系数；τi为相对滑动引起的时间延迟，通常为冲击周期的1%～2%；N为离散谐波数量；Bj，fj和βj分别为谐波的幅值、频率和相位；R为随机冲击数量；fb，φb和Db分别为随机冲击引起的共振频率、相位和共振衰减系数；Ck和Tk分别为冲击的幅值和发生时间。

滚动轴承内圈故障仿真信号的信噪比为-10.50 dB，采样频率设置为10 000 Hz，采样长度为10 000，背景噪声采用高斯白噪声，具体参数见表2。

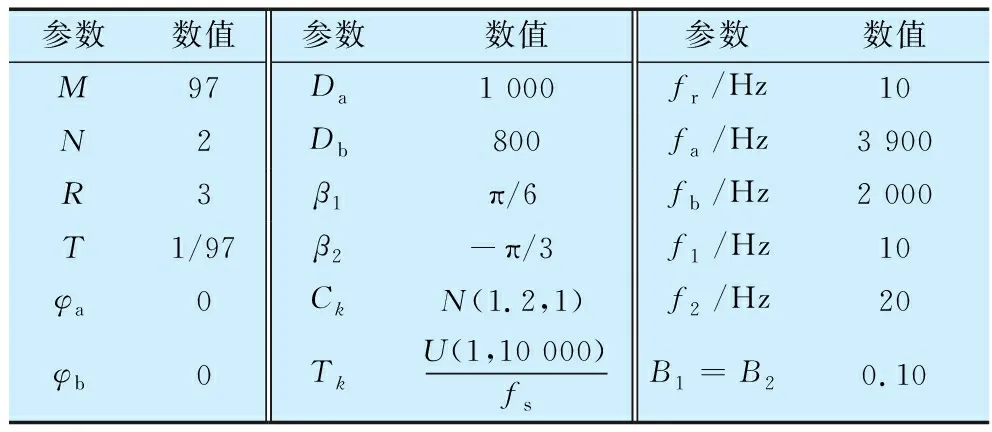
表2 轴承内圈故障仿真信号参数

3.2 仿真结果

轴承内圈故障仿真信号的时域波形及其包络谱如图1所示，时域信号中包含大量强背景噪声，周期性冲击被完全淹没，包络谱中也含有大量干扰成分，只能观察到故障特征频率及其2倍频，无法准确判断轴承故障。

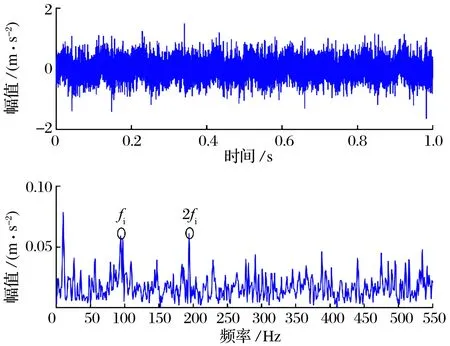
图1 内圈故障仿真信号及其包络谱

为说明结构元素长度对形态学滤波效果的影响，计算了改进形态学帽乘积算子在结构元素长度为3～300时的形态学滤波信号的评价指标MHM，结果如图2所示：随着结构元素长度的增加，MHM整体呈下降趋势；虽然MHM在局部存在较小波动，但最优结构元素长度仍然在一个较小长度区间内，可以在本文所确定的结构元素长度范围[3,30]内取到。本文所提结构元素长度范围确定方法在准确包含最优结构元素长度的同时有效地缩小了结构元素长度范围，提高了计算效率，表明了在工程应用上的优势。

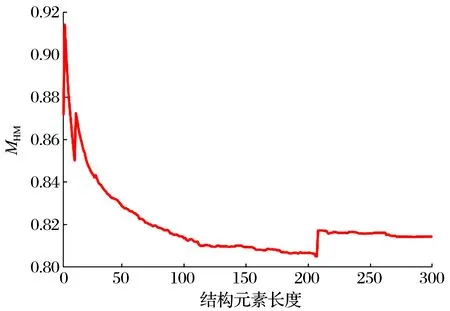
图2 不同结构元素长度下形态学滤波信号的Hoyer测度

IMHPO-DSS方法获得的滤波信号及其对角切片谱如图3所示：滤波信号中可以观察到较为明显的周期性故障冲击，背景噪声及随机冲击幅值较低，干扰成分得到了有效滤除；对角切片谱中可以清晰地观察到前5阶故障特征频率，干扰成分得到有效滤除，特征频率谱线和转频调制较为明显。

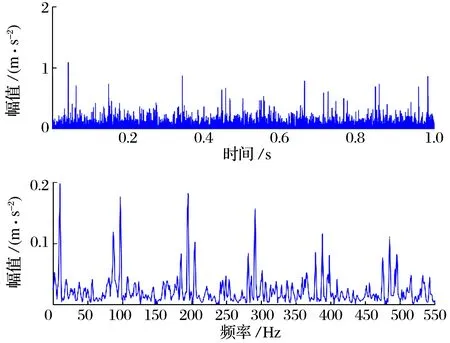
图3 IMHPO-DSS方法滤波结果及其对角切片谱

4 试验结果

采用铁路轴箱轴承的试验数据验证IMHPO-DSS方法在实际轴承故障诊断中的有效性，轴箱轴承试验台的结构如图4所示，主要由驱动装置、轮对、加载装置和控制系统组成，沿轴箱垂直方向安装了加速度计收集振动信号，采样频率为12.8 kHz，采样长度为8 192个采样点。轴箱轴承的参数见表3，分别对轴承的外圈故障和滚动体故障进行试验，故障由人工植入，局部缺陷深度为0.2 mm，宽度为0.6 mm。

(a)试验台

表3 试验中使用的铁路轴箱轴承参数

为验证IMHPO-DSS在提取轴承故障特征时的优势，同时采用MGPO-DSS和MHPO-DSS进行对比分析，并引入修正的特征频率强度系数[18]进行量化比较，对不同方法增强冲击特征的性能进行评价，即

CCFI=

(23)

式中：S和K分别为频谱中特征频率和频率分量的谐波数量；A为频谱幅值；fm和fj分别为轴承故障特征频率和谱频率，j=1,2,…,K；f1和fK分别为频谱的下限频率和上限频率，通常f1=0。CCFI表明了整个频谱中故障特征频率的凸显程度，其值越大，故障检测性能越好。

4.1 转速590 r/min时的轴承外圈故障检测

外圈故障轴承振动信号如图5所示：故障冲击特征受到背景噪声的严重污染，难以在时域图中观察到；原始信号的包络谱中仅能观察到轴承外圈的特征故障频率fe(71.80 Hz)及其2倍频且幅值较小，难以准确判断轴承故障。

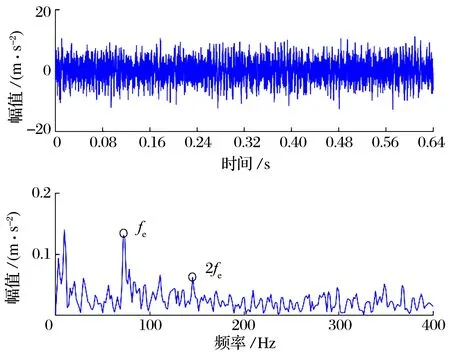
图5 外圈故障轴承振动信号及其包络谱

不同方法对轴承外圈故障信号的滤波结果及其对角切片谱如图6所示。

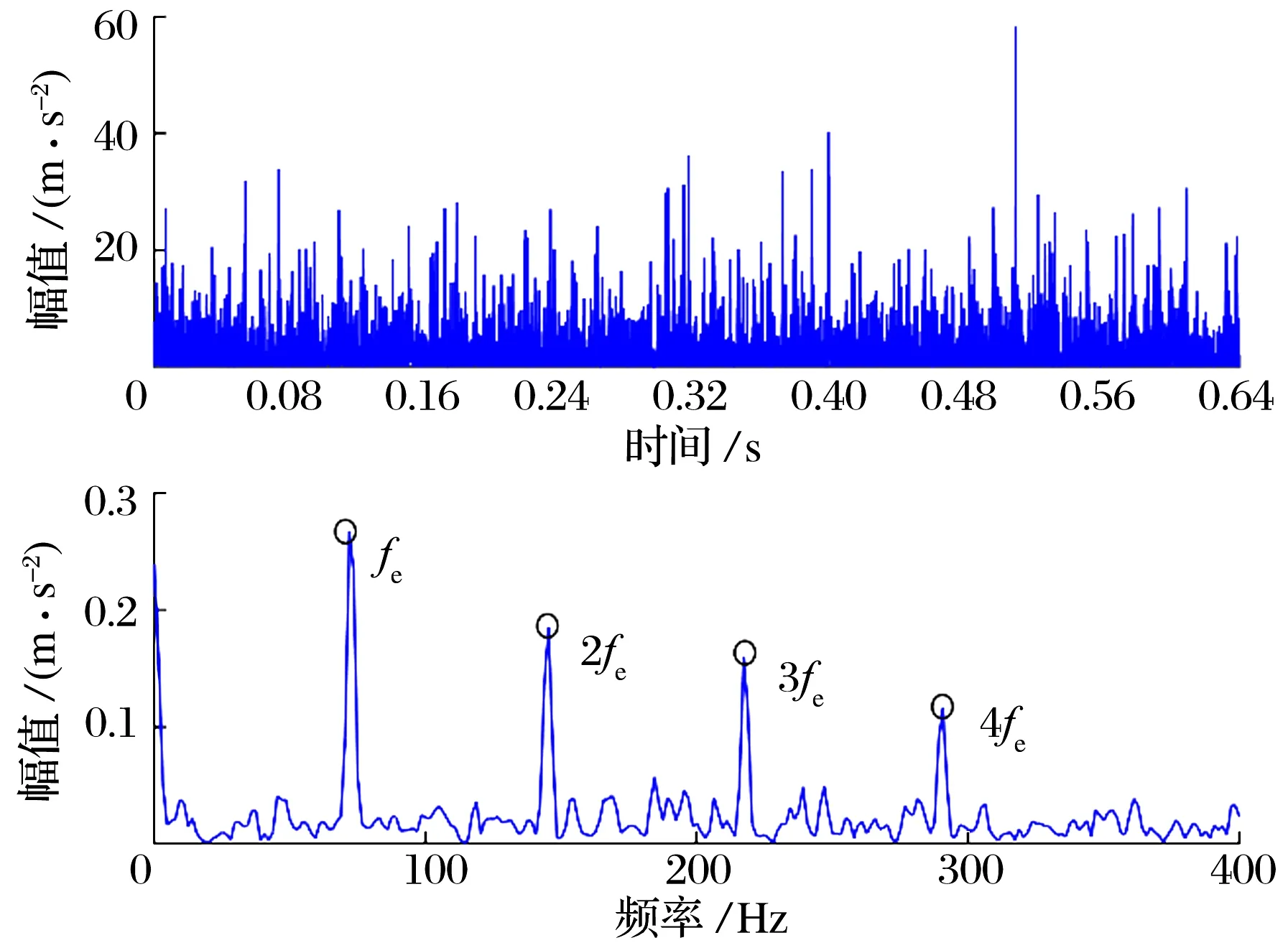
(a)IMHPO-DSS方法

由图6可知：与形态学梯度乘积算子和形态学帽乘积算子相比，改进形态学帽乘积算子滤波后的时域信号中可以观察到较为清晰的周期性故障冲击特征，且背景噪声及干扰成分的幅值较低，得到了有效滤除；形态学梯度乘积算子滤波后信号的对角切片谱中虽然可以观察到轴承外圈及其前3次谐波的故障特征频率，但2次谐波及3次谐波处存在幅值较高的干扰谱线；形态学帽乘积算子滤波后信号的对角切片谱取得了与IMHPO-DSS相似的提取效果，前4阶故障特征频率较为清晰，但干扰成分较为明显且故障特征频率谱线的幅值低于IMHPO-DSS；而改进形态学帽乘积算子滤波后信号的对角切片谱中可以观察到轴承外圈及其前3次谐波的故障特征频率，且干扰成分幅值较低，特征频率较为凸显。不同方法滤波结果的量化指标见表4，由表可知IMHPO-DSS方法的CCFI值最大，更直观地表明了其在周期冲击提取方面的优势。

表4 不同方法提取轴承外圈故障特征时的量化指标

4.2 转速582 r/min时的轴承滚动体故障检测

为进一步验证IMHPO-DSS方法对轴承故障诊断的全面性，对滚动体故障信号进行分析，所采集滚动体故障轴承振动信号如图7所示，周期性冲击被淹没在背景噪声中，故障无关分量干扰过大，原始信号包络谱中仅能识别滚动体故障特征频率fb。

图7 滚动体故障轴承振动信号及其包络谱

IMHPO-DSS方法对滚动体故障轴承信号的滤波结果及其对角切片谱如图8所示，对角切片谱中可以观察到滚动体及其前4次谐波的故障特征频率，虽然在3次谐波处存在部分干扰谱线，但干扰谱线的幅值较低，故障特征频率谱线仍然较为突出。不同方法滤波结果的量化指标见表5，由表可知：IMHPO-DSS方法的CCFI值大于另外2种方法，进一步表明其故障检测性能在3种方法中最优，也验证了该方法在轴承故障诊断中的有效性和优势。

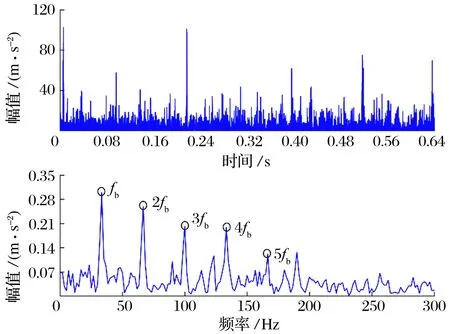
图8 IMHPO-DSS方法对滚动体故障轴承信号的滤波结果及其对角切片谱

表5 不同方法提取轴承滚动体故障特征时的量化指标

5 结语

提出了一种增强的滚动轴承故障诊断方法IMHPO-DSS，用于强背景噪声干扰情况下滚动轴承故障特征提取并实现轴承故障诊断。仿真和试验结果表明：

1)相比于形态学梯度乘积算子和形态学帽乘积算子，由2种新形态均值帽算子构造的改进形态学帽乘积算子能够更有效地提取轴承振动信号中的故障冲击特征。

2)基于振动信号极小值点的结构元素长度范围确定策略合理，且提出的结构元素长度选择方法能够有效筛选最优结构元素长度下的形态滤波结果。

3)相比于MGPO-DSS和MHPO-DSS方法， IMHPO-DSS方法能够更好地提取强噪声干扰下的轴承故障冲击特征并检测轴承故障，是一种全面、有效的滚动轴承故障诊断方法。