结合人工蜂群优化的粗糙K-means聚类算法

叶廷宇，叶 军,2+，王 晖,2，王 磊,2

1.南昌工程学院 信息工程学院，南昌330000

2.江西省水信息协同感知与智能处理重点实验室（南昌工程学院），南昌330000

-means 是一种简单、实用、高效并得到广泛应用的聚类算法，但该算法在处理模糊、不确定数据聚类时有局限性。为此，Lingras等人引入粗糙集理论对其进行改进，提出了一种粗糙-means 聚类算法，该算法把确定属于某个簇类的数据划分到下近似集，不能确定属于某个簇类的模糊数据归为边界集，较好地解决了模糊、不确定数据聚类问题。但粗糙-means 聚类算法采用人为设置固定权重和阈值方式影响了聚类精度，以及初始中心的随机选取导致聚类结果稳定性降低。研究者从不同角度提出了改进算法，文献[3-4]结合模糊集，引入了模糊隶属度，通过隶属度计算下近似和边界集中对象的权重，改变了所有对象取相同权重值的问题，增强了算法边界处理能力。文献[5-6]提出了一种根据每次迭代的聚类结果动态地确定下一次迭代聚类中样本点的自适应权重方法，改进了原算法对经验权重的依赖。文献[7]引入粒计算理论，运用组合法寻找初始聚类中心，并且通过动态调整上近似集和边界集的权重,避免了孤立点的影响。文献[8]提出了一种基于香农熵理论熵的加权多视角协同划分模糊聚类算法，给出了多视角自适应加权方法，提高了聚类性能。文献[9]用上近似取代了聚类中心更新公式中的边界集，以相对距离取代绝对距离作为相异度的判断标准，有效减小了离群点影响。文献[10]在欧氏距离中引入权值系数来初始化聚类中心，给出了一种自适应确定值的方法，改变了传统随机给定值的方式，提高了稳定性。文献[11-12]结合群智能优化算法，分别用遗传算法和蚁群算法改进了初始中心点选择方式，降低了初始中心点的敏感性和数据差异性带来的不利影响。文献[13]引入区间2-型模糊集度量概念，以此自适应调整边界区域的样本对交叉簇类的影响系数，削弱了边界区域对小规模类簇的中心均值迭代的影响。文献[14-15]提出了一种以局部密度和距离的混合度量方法来确定边界区域的对象归属，给出了一种鲁棒学习策略寻找到最佳簇类数，提高了交叠类簇的聚类精度。文献[16-17]引入了一种对簇类不均衡程度的自适应度量方法，提出了以类簇不平衡程度作为自适应调整权值的粗糙模糊均值聚类算法，提高了聚类效果。文献[18]提出了一种以维度加权的欧氏距离计算样本的密度和权重的方法，以此为基础选择个聚类中心，降低了初始聚类中心选取的敏感性。文献[19]定义了一种点与集合的计算方法，通过不断找出满足一定数量离集合最近点来得到个聚类中心，提高了初始聚类中心的稳定性。

随着聚类的应用领域不断扩大，其研究价值凸显，进一步提高聚类质量是广大研究者一直努力的目标。人工蜂群算法（artificial bee colony，ABC）是较晚涌现出的群智能算法。一些研究结果表明，人工蜂群算法在求解连续优化问题时性能要优于蚁群、遗传算法和粒子群优化算法。本文将聚类看作一个组合优化的问题，引入ABC 算法进行了改进：一是设计了更为合理的自适应调整上近似、边界权重和阈值方法，并且在此基础上定义了新的聚类中心更新计算公式；二是构造了蜜源适应度函数引导蜂群向最优秀的蜜源进行全局搜索，且避免搜索中陷入局部最优；三是以ABC 算法每次迭代求得的最优解作为初始聚类中心并同时进行聚类迭代，克服了原算法对初始聚类中心敏感等问题。实验结果表明，本文算法提高了聚类效果。

1 粗糙K-means聚类及其改进算法

Lingras 等人把粗糙集的上、下近似两个算子引入-均值算法中，提出了粗糙-means 聚类算法，其主要内容如下:

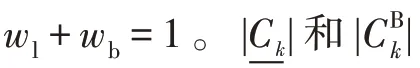
该算法主要思想是：以是否存在其他聚类中心与对象的距离与最小距离的差小于阈值为依据，把待分类对象分配到上近似或下近似集，并由式（1）更新聚类中心的位置，不断重复这个过程，直到每个聚类中心不变。

在后续大量的改进算法中，典型的有Mitra等人提出的粗糙模糊-means 算法，该算法在考虑下近似和边界集中对象分布不均匀的基础上引入模糊隶属度，改进了原算法赋予对象相同的权重的缺陷，隶属度定义为：

其得到的类C的聚类中心m更新公式为：

其中，为类别数，d为数据点x到类C中心点的距离，为模糊指数，和分别表示下近似和边界集的权重，且+=1。

随后，Maji 等人对上述式（3）隶属度定义进行了修正，定义如下：

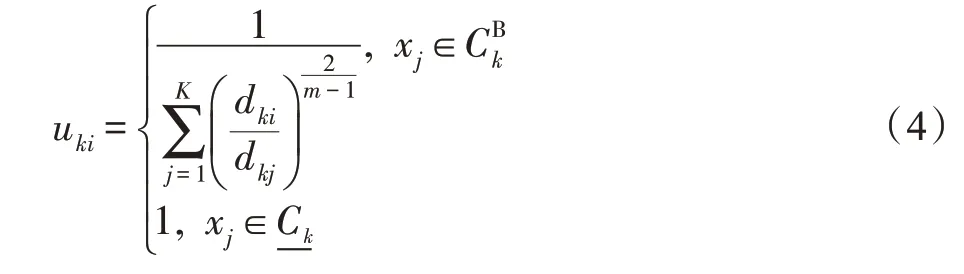
式（4）把属于下近似集即确定了归属关系的对象隶属度设为1，属于边界集即不能确定归属关系的对象需要计算隶属度，其得到聚类中心更新公式与式（3）一样。显然，式（4）更符合实际，并且减少了计算工作量。

上述这些改进方法是以对象的实际分布距离为依据，赋予对象不同的权重值，修正了下近似和边界集中所有对象取相同的权重的缺陷。但是，上述研究并没有改变、和采用固定权重的方式，其忽视了它们在迭代过程中对聚类中心的影响。

2 人工蜂群及其改进算法

Karaboga 等人模拟自然界蜂群的采蜜行为提出了人工蜂群算法，该算法将蜜源位置转化成优化问题的可行解，蜜源的含蜜量对应优化问题的适应度函数，蜂群寻找蜜源的过程是求最优解的过程。蜂群由引领蜂、跟随蜂和侦察蜂三种分工不同的个体构成。一般引领蜂个数和蜜源个数相等，且一个蜜源只有一只引领蜂开采，算法基本步骤如下：

初始化阶段：随机产生个候选解（即蜜源位置）{,,…,x},它们是维向量，并计算每个候选解的适应度，并从大到小排列，前一半为引领蜂，后一半为跟随蜂和侦察蜂。设定蜂群总循环搜索次数为，每个蜜源的可重复开采次数为。

引领阶段：引领蜂在其蜜源周围进行搜索，并由式（5）进行蜜源位置更新，保留适应度值较好的蜜源。

其中，v表示新蜜源位置，∈{1,2,…,}，∈{1,2,…,},、为随机数且≠，φ为[-1,1]内的随机数，其控制着x邻域的搜索范围。

跟随阶段：跟随蜂在获得引领蜂传达的蜜源信息后，采用轮盘赌方法，由式（6）得到的概率选择引领蜂，然后跟随蜂依据式（5）在蜜源的领域产生一个新的蜜源，并且比较前后两个蜜源的适应度值，保留函数适应度较好的蜜源。

其中，p是第个解的选择概率；fit是第个解的适应度值；是解的个数。当引领蜂经过次循环后，蜜源不再变化，则引领蜂离开该蜜源，变为侦察蜂，随机产生新的蜜源。

人工蜂群算法具有鲁棒性强、搜索能力强等优点。但存在容易陷入局部最优、后期收敛速度慢等问题，研究者们提出了多种改进方法。如Wang等人针对不同问题设计了与之对应的目标函数，提出一种多策略蜂群算法；Gao 等将差异进化算法与全局最优粒子改进的蜂群算法相结合，提出了一种收敛速度更快的算法，该方法将群体最好解的信息引入到候选蜜源的生成中,位置更新公式修改为：

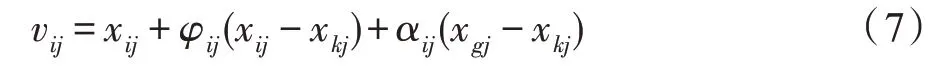
其中，x为迄今蜂群找到的最好蜜源，α∈[0,1]。本文借鉴Gao 等构建的蜜源位置更新式（7）来优化本文算法。

3 人工蜂群优化的粗糙K-means聚类算法

3.1 下近似和边界权重的改进

在粗糙-means 算法中，聚类中心更新式（1）中的和采用的是固定的权重值，即在整个聚类过程中这两个值始终保持不变。由于聚类中心的寻找是一个不断迭代更新的动态过程，这种固定权重的方式没有客观反映下近似和边界集对聚类中心影响的程度。合理度量下近似和边界区域对于聚类中心位置更新影响的重要度，动态分配和的权值是提高聚类精度的有效途径之一。为此，文献[5]和文献[7]提出了改进方法，在分析了聚类中心初期与后期位置的变化情况下，构造了一个Logistic增长曲线：

式中，为聚类算法迭代次数，、、为函数的调节参数。从式（8）可以看出，随着迭代次数的增加，权重值逐渐增大，而逐渐减小，该曲线在一定程度上动态地反映了其对聚类中心作用的重要程度。但该曲线存在不足：一是，曲线中的调节参数、和人为事先给定，主观性强，当迭代次数不断增大时,下近似集的权重几乎没有发生变化；二是，曲线没有体现下近似和边界集中对象数量的变化情况，也没有反映不同对象在上近似和边界集中分布的差异性。文献[9]给出了一种以下近似集中对象个数和上近似集中对象个数比值的自适应确定权值公式：

文献[12]给出了一种以下近似集中对象个数和边界集中对象个数比值的自适应确定权值公式：

式（9）和式（10）以样本对象的归属变化来动态确定和的权重值，客观上体现了在聚类过程中上、下近似集和边界集中数据对象数量的此消彼长动态变化情况。但是，仅以上、下近似集和边界集中对象个数来确定权重，无法反映类内和内间样本对象分布的差异性。事实上，同一类别内，数据集中的对象相对于聚类中心的距离分布不尽相同，其对聚类中心的作用不一样。不同类别间，数据集中的对象对于聚类中心的重要度也存在区别。对于和权重值的确定，不仅要考虑下近似和边界集中对象数量变化的影响，也要体现对象对于聚类中心因距离分布差异性带来的影响。综合这些因素，本文给出一种自适应动态调整下近似和边界集的权重方法。

设x为任意类别C下近似集中的对象，m为C的聚类中心，则下近似集中对象到聚类中心的距离分布为：

设x为任意类别C边界集中的对象，m为C的聚类中心，则边界集中对象到聚类中心的距离分布为：

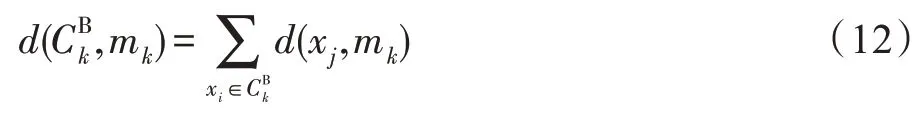
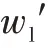
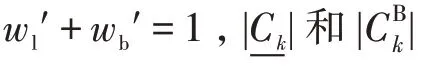
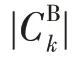
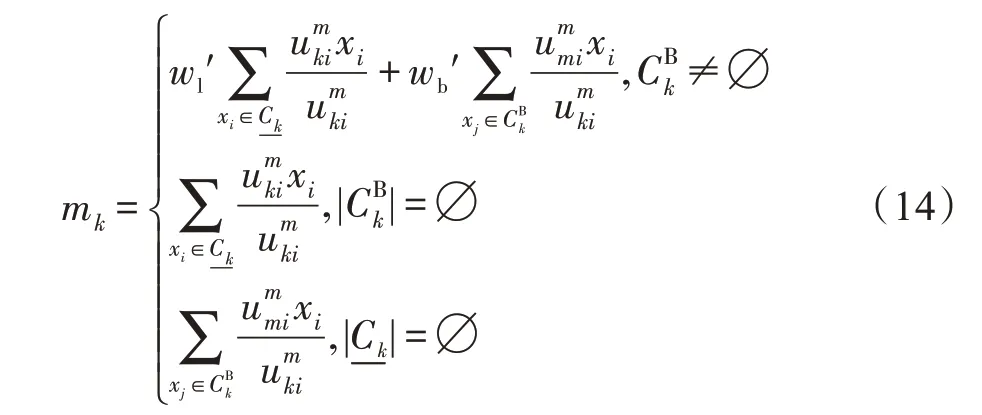
3.2 阈值自适应改进

阈值决定了样本对象是划分到类别中的上近似还是下近似集中。在经典的粗糙-means 算法中是人为给定的一个定值，这个值不会随迭代而变化，这影响了对象的精确划分。文献[5]给出了一种动态改变的方法：

其中，为迭代次数，＞1。式（15）虽然可以动态调整，但其没有合理将对象划分到所属类别的集合中。一个好的阈值应能够明确区分出样本所属的区域，得到的划分中样本归属的不确定性小。从聚类过程对象变化情况来看，开始时，对象的归属关系不明确，应该大一些，使得对象大多划入上近似集；随着迭代次数增加，对象的归属关系变得明朗，越来越多的对象划入类的下近似集，应该小一些。而式（15）随着迭代次数增加反而变大，这会让一些本该划分到下近似集中的对象划归到了边界集中，使对象归属的不确定性较大，从而导致聚类精度显著下降。

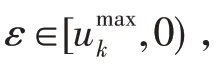
其中，是迭代次数，＞1，其对应的阈值曲线如图1所示。

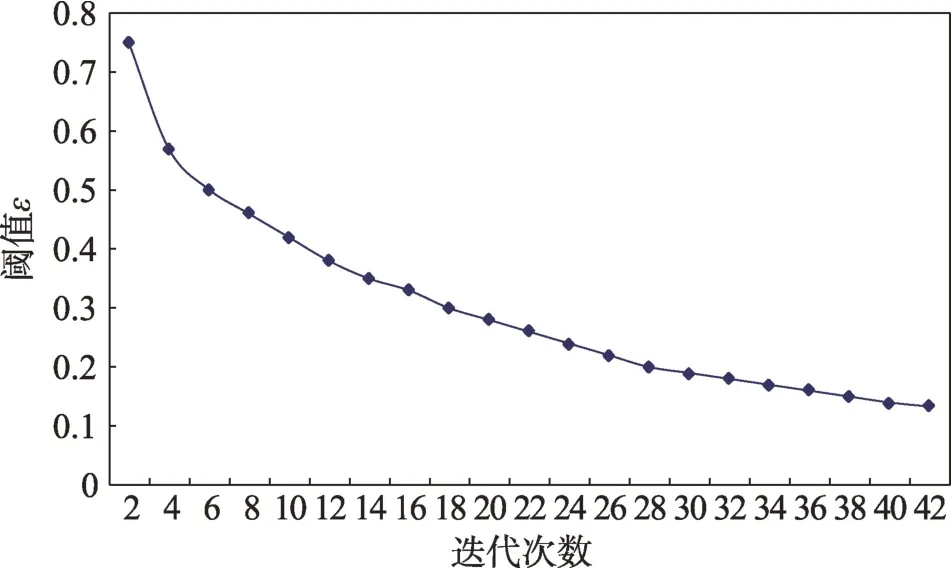
图1 自适应阈值的取值曲线Fig.1 Curve of adaptive threshold

从图1 可以看出，随着迭代次数增加，逐渐变小，越来越多的对象被划分到下近似集即确定集中，得到划分中对象归属的不确定性不断变小。显然，逐渐变小可以加快对象被划归到下近似集中的步伐，有效减少迭代次数，从而提高算法的收敛速度，这在后续的实验中也得到了验证。

3.3 适应度函数设计

适应度函数直接决定着蜂群的进化方向、迭代次数以及解的优劣。在ABC 算法中，吸引蜂群的主要因素取决于蜜源的含蜜量的多少，蜜源含蜜量越多，则代表它所处的位置好，其吸引能力就强，由此得到的适应度函数值越优。为使同一类别集合中的对象最大程度相似，而不同类别集合中的对象最大程度相异，本文通过定义类别内聚集度和类别间离散度函数来构造目标函数，并以此来寻找最优的初始聚类中心并进行聚类。

（类内聚集度函数）设对象集={,,…,x},有个样本，个聚类中心C={,,…,m}，则内聚集度函数为：

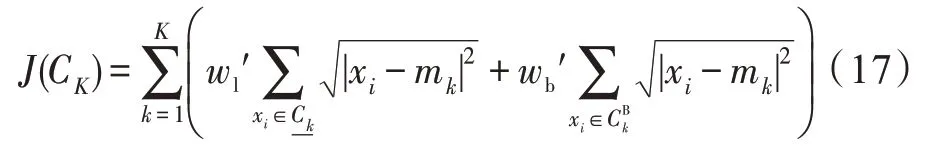
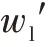
（类间离散度函数）设对象集={,,…,x}，有个样本，个聚类中心C={,,…,m}，则聚类中心的类间离散度函数为：

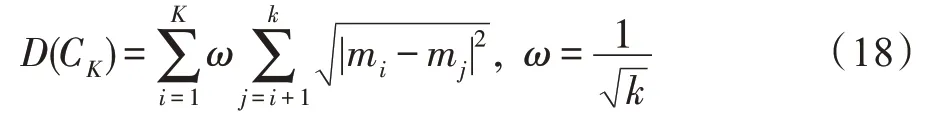
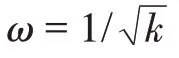
（适应度函数）适应度计算如下：

其中，(C)为类内聚集度函数值，(C)为类间离散度函数值。在式（19）中，类内聚集度距离越小，类间离散度距离越大，适应度函数值也就越大，获得的聚类效果越好。

3.4 算法实现步骤

本文算法的核心思想是以蜂群每次迭代得到的蜜源位置作为新的聚类中心，并在此基础上进行粗糙-means聚类，交替进行。算法将适应度函数fit的值代表蜜源的质量，由式（19）可知，fit值越大，蜜源的含蜜量越高，这样既保证了每个类别内的样本对象最大程度聚集，不同类别之间的距离尽可能离散，从而可以避免孤立点的影响，提高了算法的鲁棒性，并有效减少迭代次数，在寻找到最优的聚类中心的同时得到最佳聚类结果。算法的流程步骤如下：

给定类别个数，初始阈值，引领蜂和跟随蜂个数各为，最大迭代次数，控制循环上限数；当前迭代次数，初始值为1。

根据式（19）计算各个蜜源的适应度值，并按大小排序，将前一半设置为引领蜂，后一半为跟随蜂。

引领蜂按式（7）在邻域内搜索新的蜜源，采用贪婪选择原则，若新蜜源适应度值大于原蜜源值，则更新蜜源位置；否则，保持不变。搜索完成后，由式（6）计算概率p。

依据概率p，跟随蜂基于轮盘赌规则选择引领蜂，完成所有选择后，按式（7）进行邻域搜索，同样按照贪婪原则保留适应度值高的蜜源。

若有引领蜂在次迭代后，蜜源位置不改变，则引领蜂变为侦察蜂，并随机产生一个新的蜜源位置。

若达到最大迭代次数，则算法结束并输出个簇类，否则转到步骤3，=+1。

3.5 算法时间复杂度分析

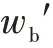
与传统的粗糙-means 算法时间复杂度(×××)相比，本文算法运算次数更多。遗传算法改进的粗糙-means算法时间复杂度为(+×××)，蚁群算法改进的粗糙-means 算法时间复杂度约为(××××)，其中为蚁群个数。显然，本文算法运算次数比文献[11]和文献[12]算法要少。但是，每执行一次算法，本文算法的运算量稍大一些。

4 实验结果分析

为验证本文算法的性能和效果，数据采用了UCI机器学习库中五个数据集，如表1 所示。软件环境为Win 7 操作系统及应用软件Matlab9.0，硬件为CPU Intel I5 1040 3.6 GHz，内存6 GB。性能比较采用类内距离、类间距离、准确率、误差平方、迭代次数和运行时间等指标，与文献[1]（传统的粗糙-means算法）、文献[11]（遗传算法改进的粗糙-means 算法）和文献[12]（蚁群算法改进的粗糙-means算法）进行比较。

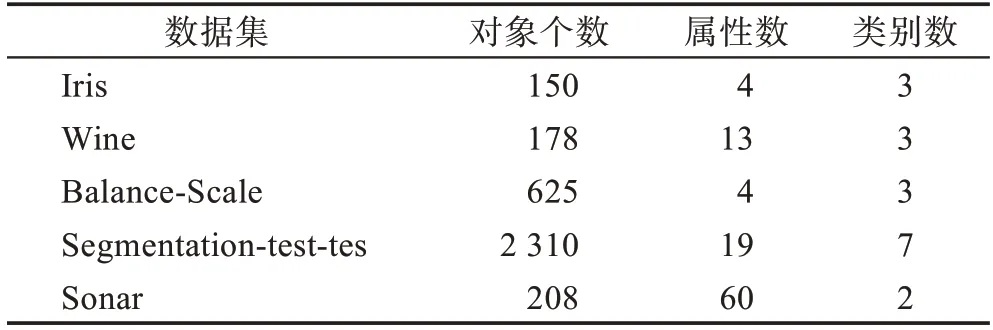
表1 实验数据集信息Table 1 Experimental dataset information

实验中相关数据设置：文献[1]和文献[11]采用的是固权重方式，对不同参数值在Iris 数据集上实验得到的结果如图2 所示，在上述其他数据集上也得到类似结果。

图2 反映了固权重方式对和值敏感，不同的取值会改变聚类中心位置，从而导致聚类准确率显著下降，这说明了固权重方式没有准确反映聚类过程中下近似和边界集对聚类中心影响的程度。因此，实验时文献[1]和文献[11]取最佳值，=0.8，=0.2，=0.05；文献[12]和本文算法采用自适应权重，∈[0.5,0)，取各数据集对应的类别数，蜂群个数＝60，＝300，＝20。分别在所选的5 个UCI 数据集上进行20次实验取平均值，实验结果如表2～表6所示。

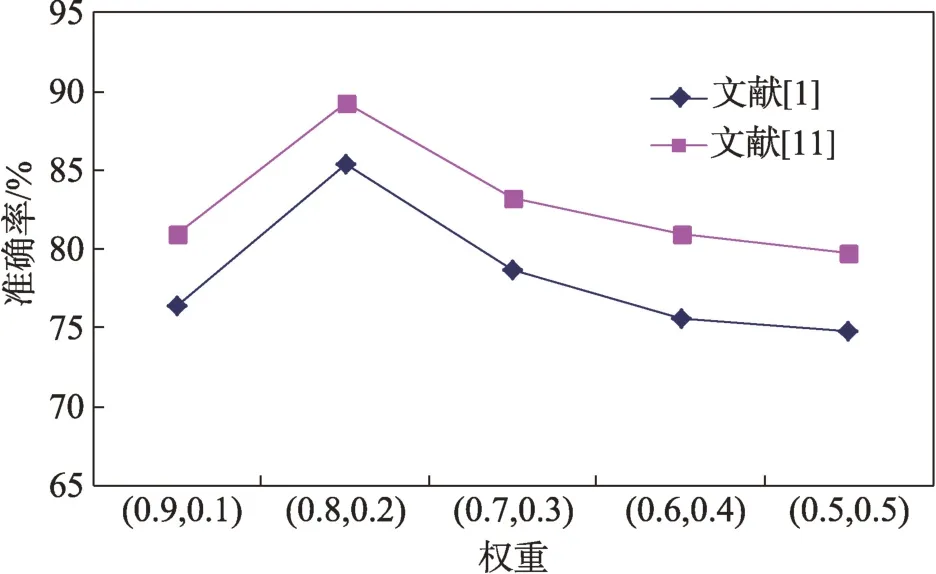
图2 Iris上不同权重取值的分类准确率Fig.2 Accuracy of different weight values on Iris

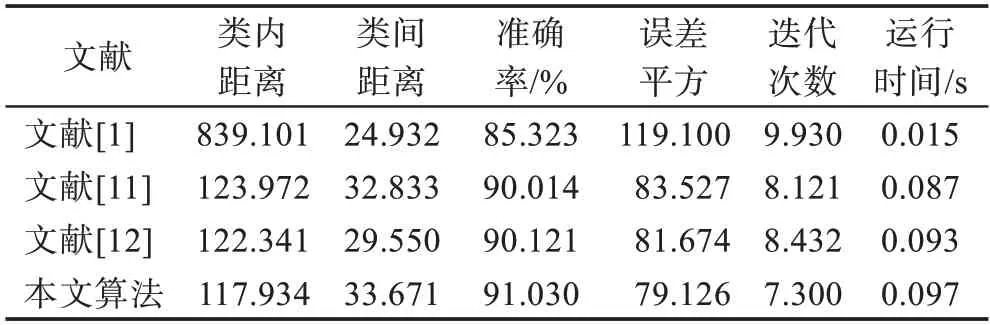
表2 Iris数据集性能比较Table 2 Performance comparison on Iris dataset

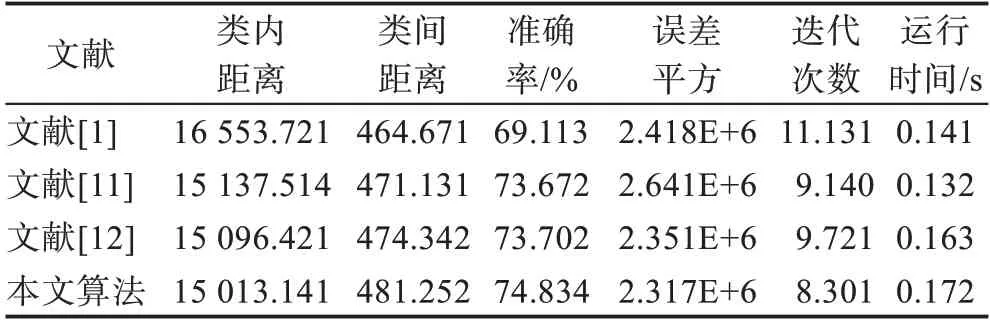
表3 Wine数据集性能比较Table 3 Performance comparison on Wine dataset dataset

表4 Balance-Scale数据集性能比较Table 4 Performance comparison on Balance-Scale dataset

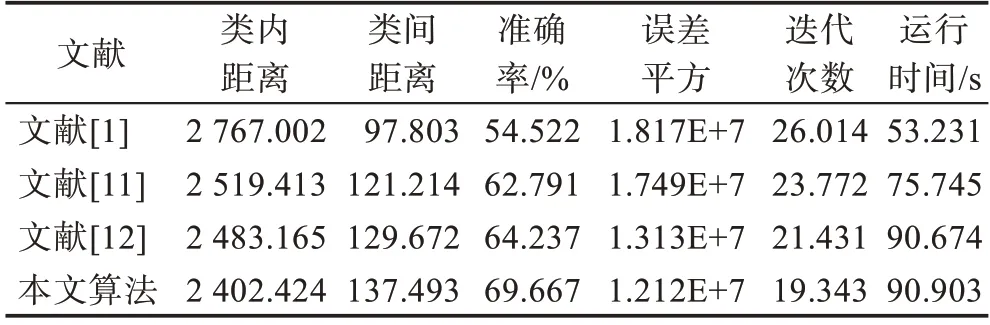
表5 Segmentation 数据集性能比较Table 5 Performance comparison on Segmentation dataset

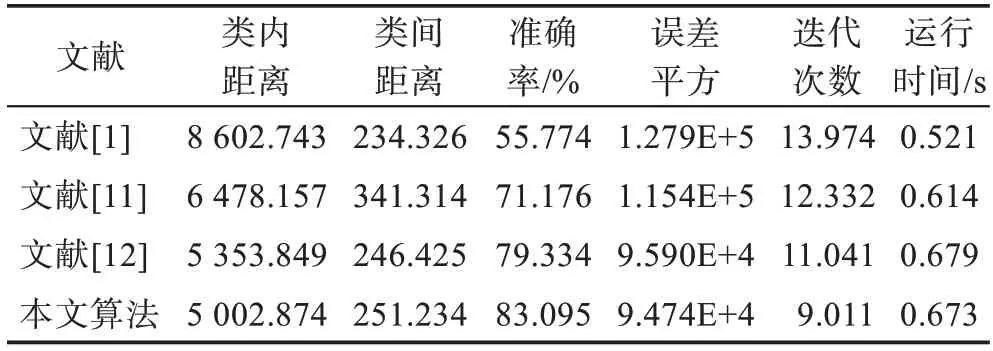
表6 Sonar数据集性能比较Table 6 Performance comparison on Sonar dataset

从式（17）和式（18）定义的类内和类间距离可知，类内距离越小，对象对聚类中心的分布越紧凑，对象相似度高；类间距离大，则不同类别中对象差异性大，得到的聚类结果误差就小。从表2～6 对比可知，本文算法在五个数据集上的类内距离、类间距离、误差平方和迭代次数四个指标都明显好于其他三个算法。准确率比较上，本文算法在上述五个数据集上好于其他三个算法。在大数据和高维数据集上，传统粗糙-means 算法聚类的准确率显著下降，本文算法依然取得了较好的效果。在运行时间上，由于本文算法每迭代一次，要计算下近似和边界集中对象相对聚类中心的距离分布和对象的隶属度，计算量比其他三个文献稍大，在Iris和Wine 数据集上程序运行耗时稍多一些，在Balance-Scale、Segmentation 和Sonar 数据集上与文献[12]相当。

对于聚类效果比较，本文采用文献[7]中用各类内对象对于整个数据中心的分布与类内对象距离的比值来衡量聚类效果，它是一种有效衡量聚类效果优劣的指标。其公式为：

由式（20）可知，同一类别中的对象分布越紧凑，距离越小；不同类别中的对象之间越离散，其到整个数据中心的距离越大。显然，比值的值越大，聚类效果就越好。实验得到的四种算法在三个数据集上距离比值的情况分别如图3～图7 所示。

从图3～图7 中的比值可以看出，本文算法得到了较好的聚类效果，而且收剑速度明显快于其他三个算法。显然，由人工蜂群优化的算法得到的聚类结果更符合数据实际分布特征。

图3 Iris数据集上距离比值比较Fig.3 Object distance ratio on Iris dataset

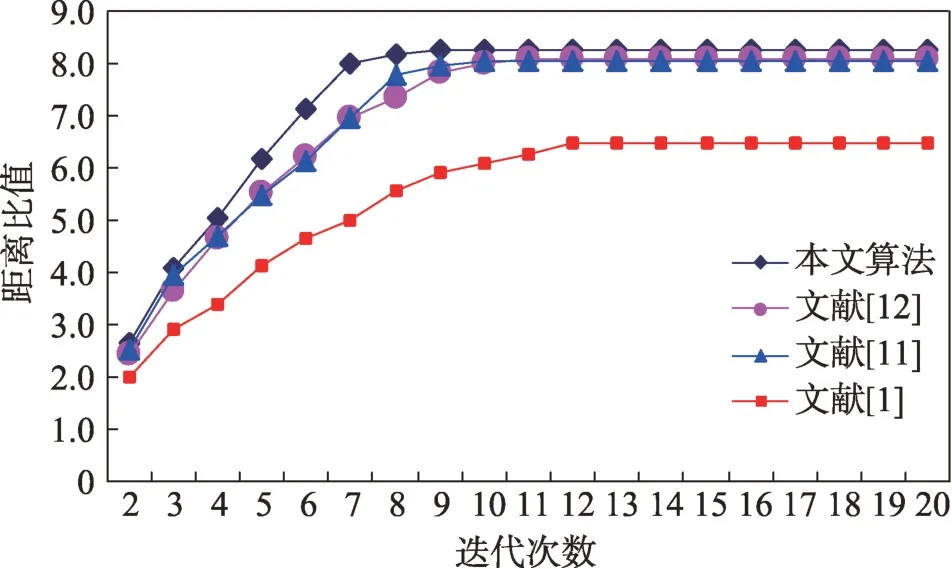
图4 Wine数据集上距离比值比较Fig.4 Object distance ratio on Wine dataset

图5 Balance-Scale数据集上距离比值比较Fig.5 Object distance ratio on Balance-Scale dataset

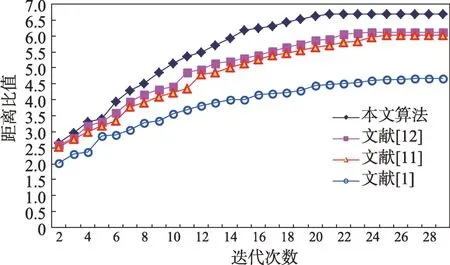
图6 Segmentation 数据集上距离比值比较Fig.6 Object distance ratio on Segmentation dataset

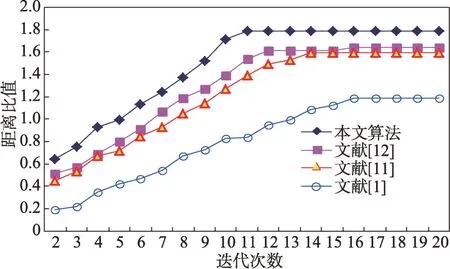
图7 Sonar 数据集上距离比值比较Fig.7 Object distance ratio on Sonar dataset

5 结束语

本文结合人工蜂群算法，在借鉴研究者们研究成果的基础上，对粗糙-means 聚类算法进行了改进。在下近似和边界集权重分配改进方面，本文给出的自适应动态确定下近似和边界集的权重方法，既考虑了下近似和边界集中对象数量变化的影响，也没有忽略对象对于聚类中心因距离分布差异性带来的影响，整体上提升了算法的性能。在初始聚类中心优化方面，每次迭代以蜂群找到的最好蜜源更新聚类中心位置并进行聚类，为改善算法因对初始数据的敏感性带来的不利影响提供了思路。但是，本文算法中设计的自适应权重调整方式增加了算法的计算工作量，在高维且样本数量多的数据集上更为明显；另外，簇类数值是事先根据已知簇类数的数据集给定好的。事实上，在实际应用中，很多时候事先并不知道数据集被分成多少簇类最合适。因此，簇类数的选取对算法的聚类效果影响较大。后续将结合文献[14]和文献[15]提出的对未知簇类鲁棒学习策略，进一步研究自适应寻找最佳类别数的方法。此外，优化本文算法的计算工作量，降低算法的时间复杂度，提升算法的执行效率也是今后要继续开展的研究工作。