多样性正则化极限学习机的集成方法

陈 洋，王士同

1.江南大学 人工智能与计算机学院，江苏 无锡214122

2.江南大学 江苏省媒体设计与软件技术重点实验室，江苏 无锡214122

集成学习，在过去的几十年里已经成为一个成熟的研究领域，是一种建立基分类器的基础上进行有效融合集成形成强分类器的方法，其中包括两个主要工作：一是基分类器的构建；二是多分类器的融合集成方法。直观地说，分类器集成成功的关键是基础分类器表现多样性。这种认识首先在理论上被误差模糊分解证明是正确的。=ˉ-ˉ，其中是整体的均方误差，ˉ是组成学习者的平均均方误差，ˉ是整体和组成学习者之间的平均差异。这种分解意味着，只要ˉ是固定的，组件学习者之间的较高差异就会导致更好的集成。此外，偏差-方差分解分析的学习方法也被用来解释分类器集成的成功。Brown声称，从信息论的角度来看，一个集合中的多样性确实存在于分类器之间的许多层次的相互作用中。这一工作启发了Zhou 等人从多信息的角度出发，提出应该最大化互信息以最小化集合的预测误差。随后，Yu 等人提出，在个体学习者的多样性正则化机器（diversity regularized machines，DRM）中以成对的方式使用个体学习者的多样性，可以降低假设空间的复杂度，这意味着控制多样性在集成方法中起到正则化的作用。上述理论都证实了个体学习者的多样性是集成学习的关键。

一些众所周知的算法，如Bagging和Boosting被认为是解决模式分类任务有效方法，Bagging 和Boosting 算法都是基于训练数据集的重采样方法，Bagging 算法是并行集成，而Boosting 是串行提升，都是使用输入数据的不同训练子集和同样的学习方法生成不同模型。2011 年基于Bagging 的集成分类器，即Bagging-ELM，已经得到了广泛的研究，并被证明可以在准确性方面显著提高极限学习机（extreme learning machine，ELM）的性能，但是由于计算量大，不适用于大规模数据集。2015 年Jiang 等人利用主成分分析对人脸特征进行约简，并将ELM 嵌入到AdaBoost 框架中进行人脸识别，实验证明，AdaBoost方法可以显著提高ELM 性能。2018 年一种基于代价敏感集成加权极限学习机的新方法（cost-sensitive ensemble weighted extreme learning machine，AE1-WELM）被提出，这种方法提出应用于文本分类，通过样本信息熵来度量文档的重要性，并根据文档的重要性生成代价敏感矩阵和因子，然后将代价敏感的加权ELM 嵌入到AdaBoost 中。该方法为文本分类提供了一种准确、可靠、有效的解决方案。

然而基于以上两者算法的极限学习机的集成方法都可以被解释为隐式地表达多样性，构建了不同的基本分类器。在集成学习算法中，如果术语“多样性”被明确定义和优化，就可以恰当地使用算法多样性。由于许多集成算法都是通过隐式寻求多样性而成功提出的，很自然地会考虑是否可以通过显式寻求多样性来获得更好的性能。

文献[12]中报道的一些结果表明，ELM 在回归和分类任务中都具有学习速度快、泛化性能好等显著特点。因此这种快速学习方案避免了基于梯度的优化技术中的困难，如停止标准、学习速率、学习周期和局部极小值等。但是单一的极限学习机在数据分类上是不稳定的。为了克服这一缺点，越来越多的研究人员考虑使用集成ELM，综合这些因素促使在集成学习中采用ELM 作为基础分类器。

（1）在一定程度上解决单个ELM 分类器的不稳定性问题。提高预测性能的同时，也具有很好的泛化能力和鲁棒性。

（2）10 个数据集上的实验结果表明本文所提出的基于多样性正则化极限学习机的集成方法可以更好地处理具有大量属性或样本数量的数据集。

（3）本文所提出的算法从初始化隐含层输入权重、偏置以及多样性惩罚项两个角度双重保证了最后集成模型的性能。

1 ELM 简介

近年来，ELM 的研究已有了较为迅速的进展，表现出广阔的发展和应用潜力，吸引了大量学术界和工业界研究人员的高度关注，并取得了丰硕的研究成果。本章将根据原始的ELM 算法和RELM（regularized extreme learning machines）算法详细介绍求解隐含层输出权重的方法。

ELM 最初是针对单隐层前馈神经网络（singlehidden layer feedforward neural network，SLFN）提出的，后来扩展到广义前馈网络。ELM 的显著优点在于隐藏节点参数（输入权重和偏差）的随机选择，并且网络输出权重可以通过使用最小二乘法求解线性系统来分析确定。训练阶段可以高效地完成，而不需要耗时的学习迭代，并且可以获得良好的泛化性能。如图1 所示的ELM 的网络结构模型。

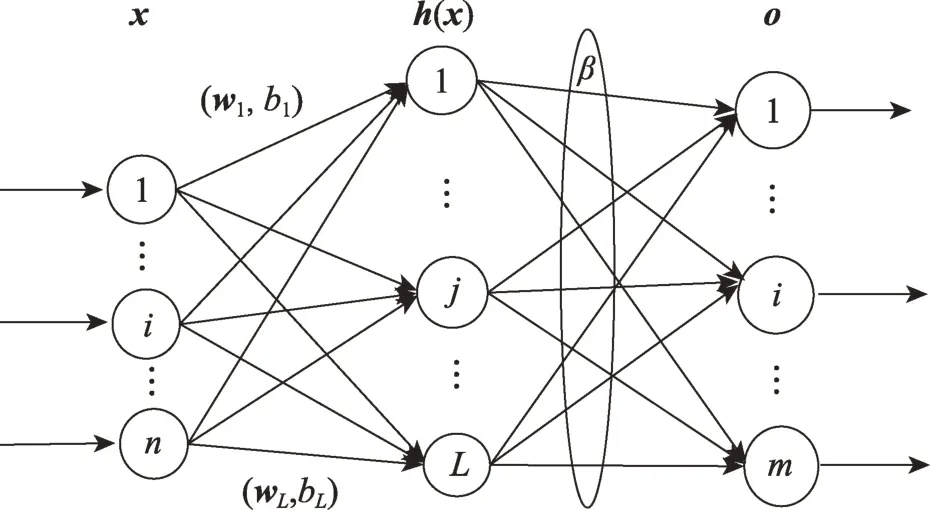
图1 ELM 模型框架Fig.1 ELM network structure

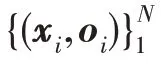
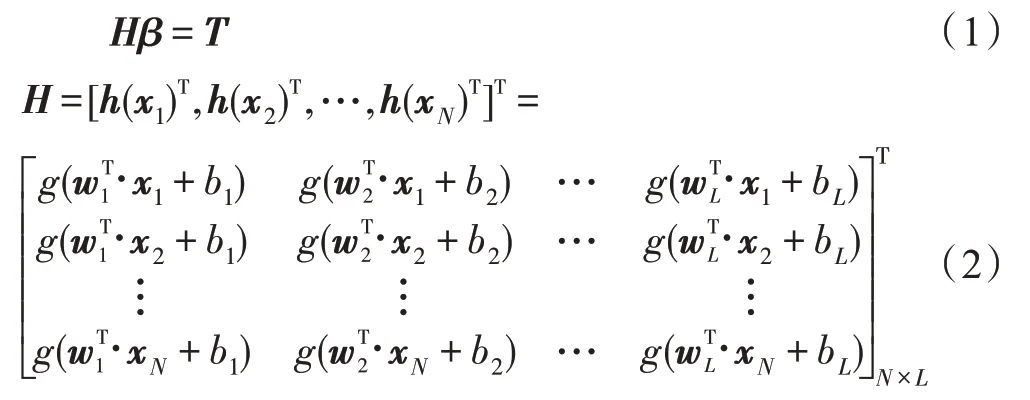
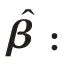
其中，表示隐层输出矩阵的广义逆矩阵。隐节点数是随机的，由通用逼近性可知激活函数无限可微分，隐含层输出近似看成连续函数。

（1）对于隐节点数等于输入样本个数，可找到矩阵，使得：

（2）对于隐节点数小于样本个数，对于任意＞0，总存在，使得：

利用最小方差寻找最优输出权重。即优化训练误差函数：

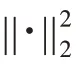
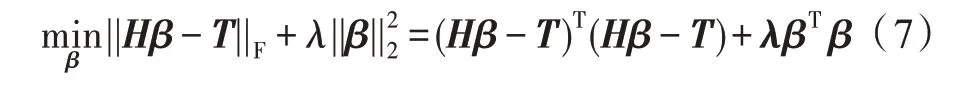
其中，是在训练误差项和正则项之间进行权衡的正则化参数。对进行微分得到：

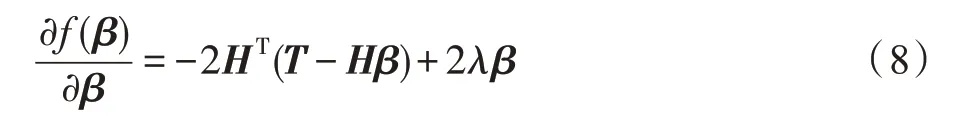
让梯度等于0，可以得到：

求解上式可以很容易地得到下面的解：

因为＞0，矩阵是正定的，又因为矩阵是半正定的，所以矩阵+是正定的。因为的出现使得矩阵+变成了非奇异矩阵，所以根据隐节点数与样本数的比较，求解可得输出权重形式如下，其中是单位矩阵：

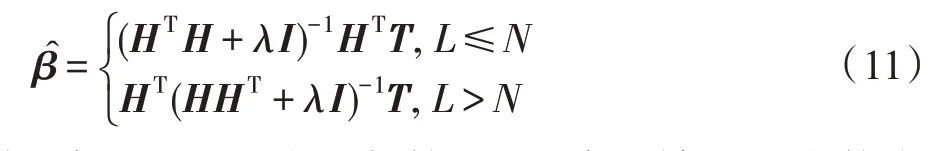
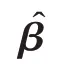
2 DRELM 模型建立

2.1 DRELM 网络结构图

集成的关键是保证多样性，一种简单的实现方法就是使用不同分布来初始化每个学习器的隐层节点参数。本文提出的基于差异性正则化极限学习机的集成方法，在生成每个ELM基学习器初始权重时选择了高斯分布和均匀分布等任意的随机分布，保证了集成时每个基学习器之间具有一定的差异性，并且隐藏层节点到输出层节点之间的权重则是通过最小二乘法求解得出，因此可知本文算法对初始值并不依赖。

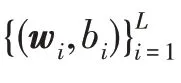
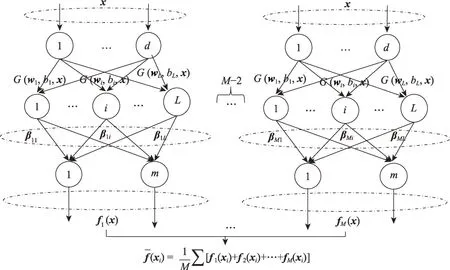
图2 多样性正则化ELM 集成学习系统模型框架Fig.2 Ensemble learning of different regularized ELM network structure

2.2 算法过程

注意到，在集成方法中虽然对于多样性应该以什么形式定义没有一致意见，但是所研究的多样性度量通常可以是成对的形式，即总多样性是成对差异度量的总和，用于度量分类有效性。这种多样性测度包括Qstatistics 测度、相关系数的度量、不一致测度、双错测度、统计测度等。因此，还考虑了一种基于成对差异的多样性形式。给定假设度量空间中的成对分集测度，考虑假设基学习器集合={,,…,c}，则可得到成对差异项的总和表达式如下：

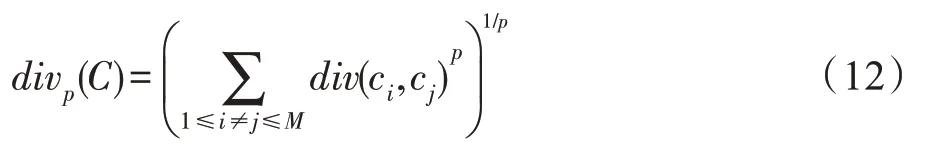
规定div({,,…,c})≥，其中，是多样性项最小值。则在对于ELM 集成问题中，改变输入权重和偏置的元素分布方式和范围，训练个不同的ELM 基学习器，′表示不同于的任意。考虑到隐点数优化问题，得到的每个ELM 的隐含层到输出层的权重矩阵的维度可能不一样。为了绕开这个问题，在本文中，将它们集成在一起时，提出一种明确的方法来管理各个基础学习者之间的差异。即将有关多样性的新惩罚项显式添加到整个集成的目标函数中。惩罚项表达式如下：

该表达式不会受不同的隐含层输出权重维度不一致的影响，多样性控制参数的值对应上式中的。在不失一般性的前提下，本文采用RELM 算法作为该算法的基础。为了提高泛化能力，本文也加入了对每个学习器的隐含层输出矩阵的泛化项，因此可以得到目标优化函数如下：

因为上式对于每个学习者是自然可分的，所以可以简化求解过程，采用了一种有效的交替优化技术。将所有′≠时的′当作已知固定量，交替优化依次求解，从数学上来说，把上面的目标函数转化为求解下面这个小目标函数：

上式分别对β求偏导得到：

正则化参数调节第三项的相对成本。较大的值会降低个体极限学习机的一致性，从而增强多样性，而较小的值则会产生一组几乎相似的极限学习机。但是存在的争议是，目标函数中的第三项使得目标函数可能不会变得凸。为了解决这样一个可能的问题，提出了以下方案来讨论参数的范围：

假设参数的上界值为，为了求出值，只要使得如下式子：

基分类器的集成及结果整合

ELM 算法中，影响网络泛化能力的一个重要因素是隐含层节点和正则化参数。一种确定ELM 中最优参数的方法是留一交叉验证策略。对于本文模型，为了确定隐含层节点的最终数目，需要计算不同隐含层节点数目时对应的留一交叉误差，最后选择误差最小时对应的隐含层节点数目。因此，为了优化隐节点数以及正则化参数，使用LOO交叉验证策略中的预测残差平方和（MSE）作为评估性能指标。

其中，为了减少MSE公式的计算复杂度和隐含层输出矩阵的重复计算，本文引用了奇异值分解（singular value decomposition，SVD）矩阵策略来分解隐含层输出矩阵：令=，其中，和均为酉矩阵，即=，=，是对角矩阵。

当≤时，=，则可以得到：

当＞时，=，则可以得到：

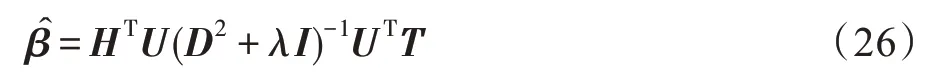
算法2 给出了基于LOO 误差的基分类器的实现方法。

基分类器的构建

设为输入训练样本个数，为初始输入样本特征维数，隐含层节点数设置为，输出层节点数为个，基学习器的数量为，则算法的时间复杂度包括两部分，即基学习器的训练步骤和基学习器的集成步骤。第一部分的时间复杂度集中于算法2 中步骤1.1 每个基学习器的隐含层输入矩阵的计算，时间复杂度为()，步骤1.2 中分别计算出每个基学习器的隐含层输出权重，时间复杂度为(+)，因此第一部分时间复杂度为(++)，其中是目标类别数。第二部分算法1 中步骤1 计算隐含层输入矩阵时间复杂度为()，步骤2 中，设迭代次数为，则步骤2 中计算更新隐含层输出权重的时间复杂度为()。因此总的算法时间复杂度为(2+++)。

图3所示为多样性正则化ELM集成方法流程图。

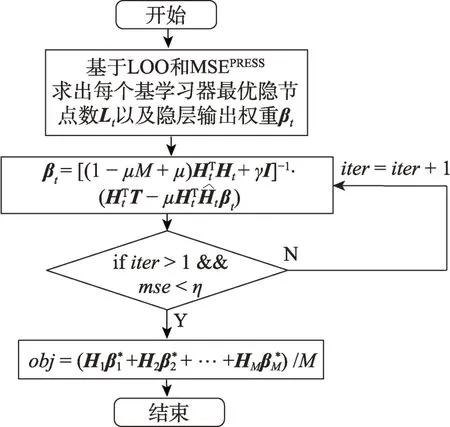
图3 多样性正则化ELM 集成方法流程图Fig.3 Flow chart of ensemble learning of different regularized ELM

3 实验及结果分析

3.1 数据集

本节通过大量数值实验来检验所提出的集成分类器的性能的分类效果，并对比了其他代表性的分类模型。为保证实验结果的真实准确，每个数据集对应的实验都进行了10 次实验，然后取其平均值和标准差作为最终结果。对于分类问题，采用常用的准确率（accuracy）作为衡量指标。实验从国际通用的加州大学欧文分校的UCI 数据库中选择了10 个分类数据集，表中涵盖了所测试的基准分类数据集的样本特征维数、训练样本数、测试样本数和类别数。表1列出了数据集的详细信息。本文所有实验均在同一环境下完成，采用在Windows 10 环境下搭建系统，计算机处理器配置为IntelCorei3-3240 CPU@3.40 GHz，内存8 GB，主算法在Matlab2016 中完成。

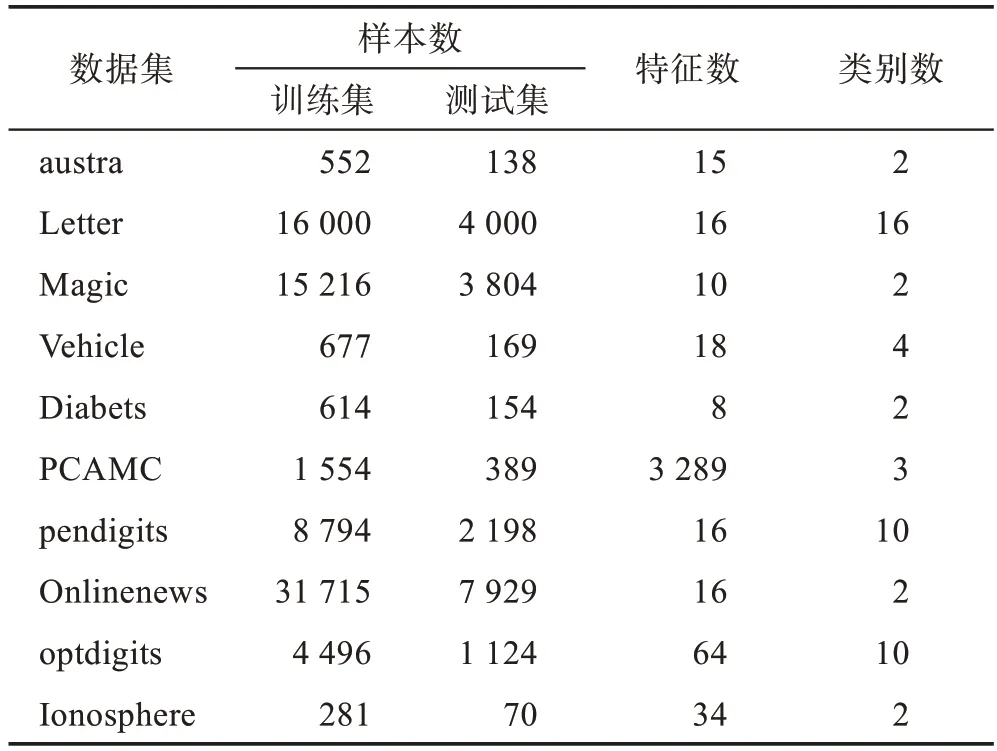
表1 UCI的10 个数据集的详细信息Table 1 Details of 10 datasets for UCI

3.2 敏感性分析

通过实验来研究泛化项系数、多样性控制参数以及基学习器数量对模型性能的影响。下面以austra 数据集为例进行敏感性分析。参数在{2,2,2,2,2}中确定，根据上一节中对参数范围的讨论，依据式（24）计算出它的上界值，为了保证值在它的有效取值范围以内，可得到参数在{2,2,2,2,2}中确定。在合适的基学习器数量（如=5）的前提下，图4（a）和（b）分别说明了在austra 数据集中，当其他参数不变时，精度随和值的增加而变化的情况。图4（c）中，探究的是基学习器数量对模型性能的影响，当正则化参数以及多样性控制参数都设置适当（如=2，=2）时，通过改变基学习器数量观察它对准确率的影响。

显然，由图4（a）和（b）可以看出，泛化项系数和多样性控制参数对DRELM 的分类准确性有相当大的影响。适当的值将有助于提高DRELM 的分类准确性。

从图4（c）可以看出，在集成学习中，基学习器的数量是影响模型性能的关键因素。一般认为，基学习器的数量越多，意味着模型的准确率越高，但当基学习器增加到一定数量以后模型性能达到最优且较为稳定时，再持续增加基学习器的数量，模型的性能反而会下降。对于本文中多样性正则化极限学习机的集成方法并不是基学习器的数量越多预测性能就越好，在本文实验所用的数据集中，最佳的基学习器数量大约为5 到6。

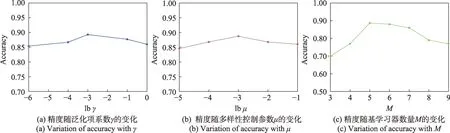
图4 austra 数据集的精度变化图Fig.4 Accuracy changes on austra dataset

3.3 参数设置

改进的二参数BP 算法对标准的Sigmoid 函数引入新的参数和，其中系数决定着Sigmoid型函数的幅度，引入参数增加了自变量值的弹性，通过调整参数可以大大改变误差曲面变化率，从而避开局部最小。对于本算法中泛化项系数使用网格搜索从{2,2,…,2}范围内搜索。对于较小的数据 集，例 如austra、Diabets 和Ionosphere 在[50：50：600]之间寻找最佳的隐节点数。像大样本数据集OnlineNews，Magic 则在[500：100：2 500]范围内搜索隐节点的最佳数目。剩余数据集在[500：100：1 500]寻找最佳的隐节点数目。各模型参数的设置详见表2。

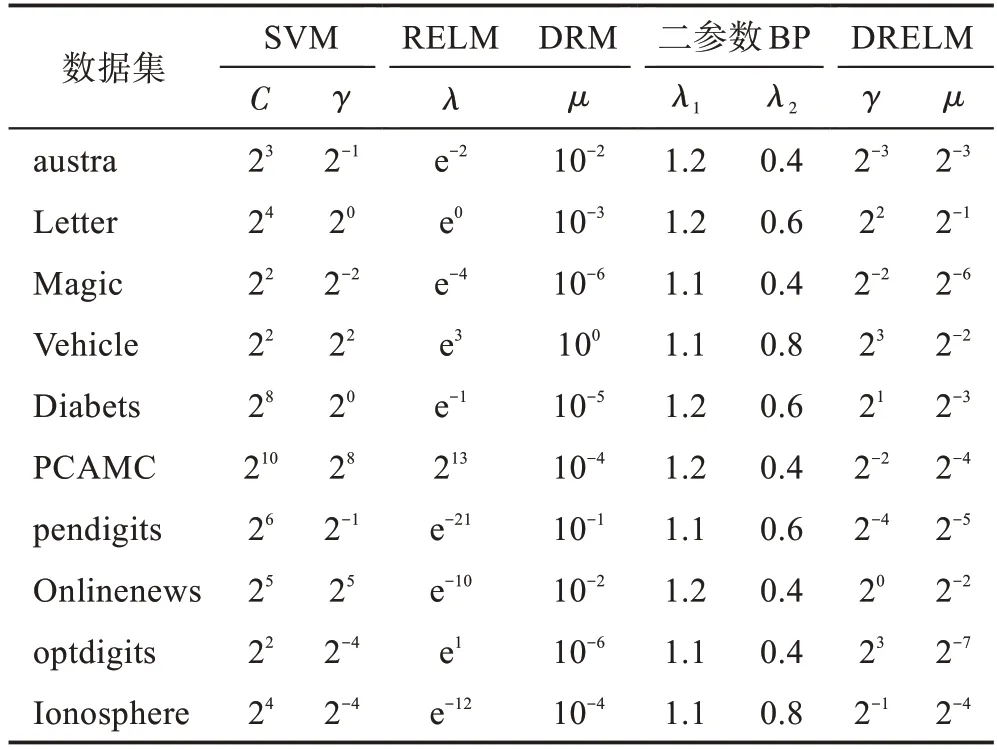
表2 用于UCI数据集的各种模型的参数设置Table 2 Parameter settings of various models for UCI datasets

3.4 实验结果

在将DRELM 算法与SVM（RBF）算法进行对比，RELM 算法与DRM 算法进行对比的时候，为了保证实验的公平性，首先，对于本文的DRELM 算法，基学习器数量设置成5 个（=5），DRM 算法也采用5 个SVM 基学习器集成的规模；其次，对于RELM 算法的隐节点数规模将设置成DRELM 算法隐节点数集成总数的规模。实验对比结果如表3 所示。

从表3 中可知各个数据集的分类准确率实验结果。针对SVM、RELM、DRM、二参数BP 和DRELM这五种算法，本文采用加粗样式标注最优测试精度，采用加粗并加下划线来标注最优标准差。由表中大多数数据集结果可以看出，DRM 算法和DRELM 算法的分类精度和标准差均较优于SVM、RELM 和二参数BP 模型。此外，尤其对于大样本或大特征维数的数据集而言，DRELM、DRM 算法的标准差明显低于其他三个算法，而DRELM 算法的标准差又明显低于DRM 算法。而RELM 算法在所有算法里面表现得相对较差。主要考虑到实验公平性，将RELM 算法的隐节点数设置成DRELM 算法所有基学习器的隐节点总数的规模，过多的隐节点数可能造成过拟合现象，从而导致它的测试精度表现得较差。

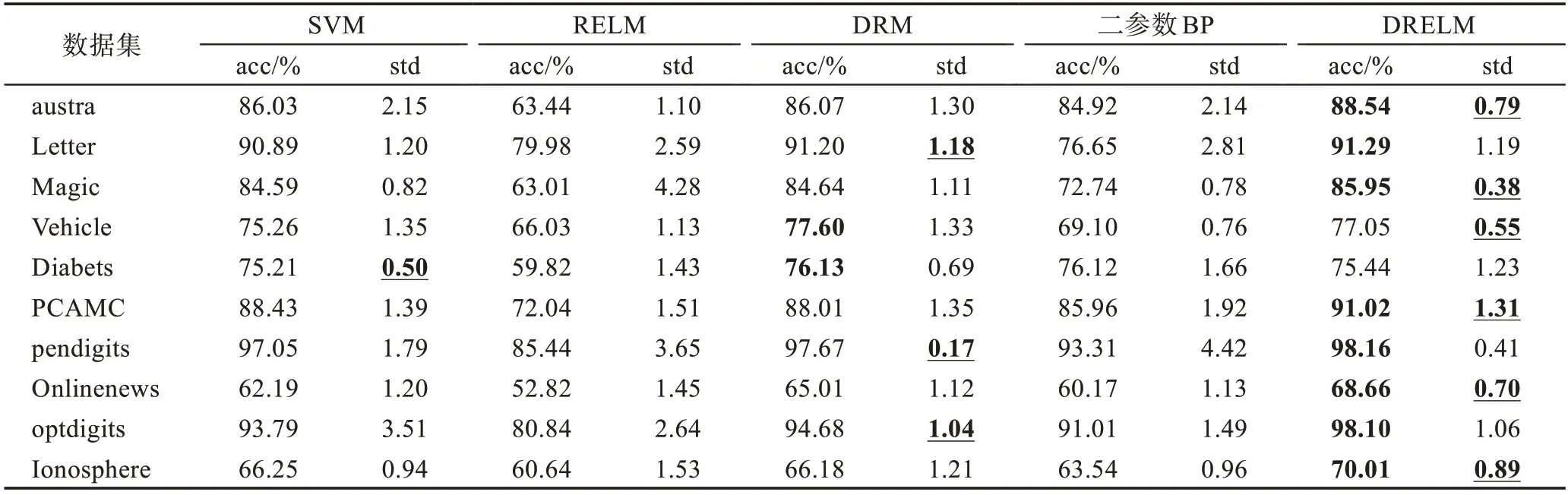
表3 各种模型对于不同数据集的测试结果与性能比较Table 3 Test result and performance comparison of various models on different datasets

在这10 个数据集中，可以发现austra、Letter、Magic、PCAMC、Pendigits、Onlinenews、optdigits、Ionosphere 数据集在DRELM 的测试精度比DRM高。同样，可以发现austra、Magic、Vehicle、PCAMC、Onlinenews、Ionosphere数据集在DRELM算法中的测试精度更加稳定集中；austra、Magic、PCMAC、Onlinenews、Ionospher 数据集在测试精度和标准差上DRELM 算法均优于DRM 算法。

并且，DRELM 算法比较原始RELM 算法，在精度提升方面最高达到了39.56%，并且标准差降低了28.18%。同时DRELM 对比DRM 算法，在精度提升方面最高达到了5.79%，但标准差方面最高有着26.45%的下降。

通过对比可以发现，在这些实验数据集中，本文介绍的DRELM 算法在精度方面优于原来的ELM 算法，也略优于DRM 算法，且具有较好的稳定性。从表4 中可知，ELM 是最快的学习者。在所有数据集上，RELM 以及本文提出的1DRELM 要比SVM、DRM 以及BP 训练耗时少得多。

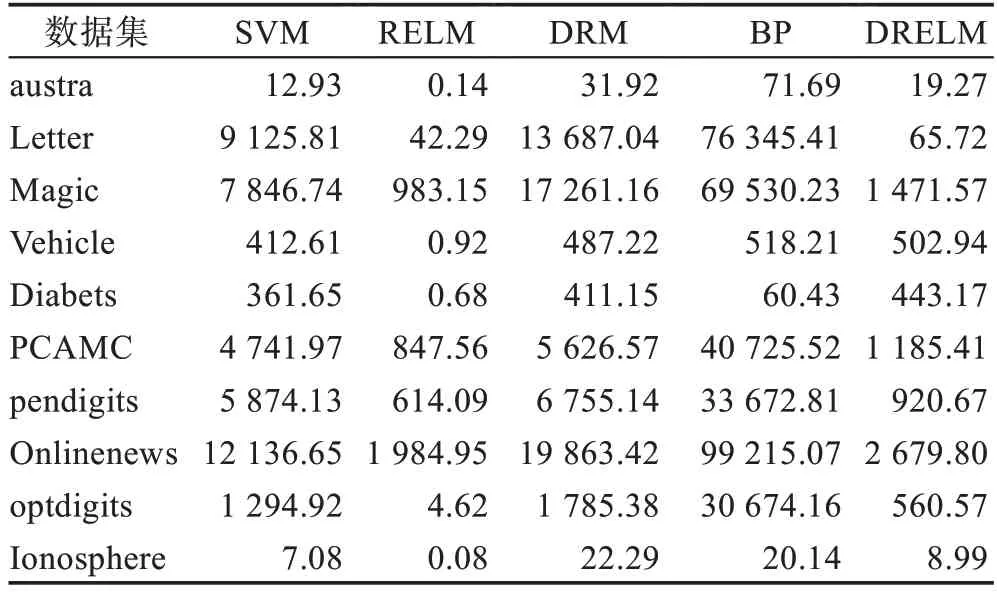
表4 各种模型对于不同数据集的训练时间比较Table 4 Training time comparison of various models on different datasets s

总的来说，改进的多样性正则化极限学习机集成算法比传统的基于梯度的方法（如BP 算法）以及ELM、SVM 具有更好的性能和稳定性，并且能以相对更短的训练时间提供令人满意的泛化性能。

4 结束语

多样性被认为是集成方法成功的关键。本文提出的算法从两方面保证了模型的多样性：首先，基学习器构建的时候，改变隐含层节点参数初始化的分布并优化得到每个学习器的最优隐含层输出矩阵和隐节点数，保证训练得到几个较为优秀而又不同的基学习器；其次，将有关多样性的新惩罚项显式添加到整个集成的目标函数中，明确控制基学习器之间的多样性。基于实验结果分析，本文方法能够提高预测性能，并在处理大数据集时表现得更加优越，也具有很好的泛化能力和鲁棒性并优于一些先进的集成方法，但仍有进一步研究的空间。例如，在实践中可能需要不同类型的基学习者进行集成学习，尽管可以通过网格搜索或交叉验证来确定正则化参数，但是相应的过程在计算上仍然是昂贵的，加快此过程的适当方法也很关键，需要深入研究。此外，进一步研究如何为特殊应用场景确定合适数量的基学习器也是值得考虑的。