复合点坝演化模式及成因分析

范洪军，王夏斌，胡光义，范廷恩，何明薇

中海油研究总院有限责任公司，北京 朝阳 100028

引言

Sadler 指出，研究精度越高，沉积体表现得越残缺、沉积过程越呈现为间断性[1]。这一点在曲流河复合点坝沉积中表现得尤为典型。胡光义等指出，曲流河沉积过程中，单个完整的点坝体基本只会发育在沉积末期，先期形成的点坝在水动力不断改造下迁移，往往遭受不同程度的破坏[2-3]。因此，经历埋藏成岩后的点坝，多以残缺体的形式与其他残缺单元镶嵌在一起，残缺体的空间几何形态通常十分复杂。复合点坝是由多期残缺点坝组合在一起形成的复合体[4-5]。曲流河点坝一直是沉积学研究的热点，前人主要从现代沉积、野外露头、沉积模拟、地下构型表征及开发生产等方面开展研究。现代沉积方面，赵晓明等通过对加拿大Beaver 河现代点坝的分析，建立了平移型点坝的机理模式类型[6]；Cosma等研究了意大利威尼斯潮汐点坝现代沉积，分析了水动力对点坝形态的影响[7]。野外露头方面，Mitten等通过解剖犹他州点坝露头剖面，统计了不同级次下构型单元的定量规模[8]；姚宗全等识别了准噶尔盆地侏罗系齐古组露头上的点坝砂体，总结了点坝的平面与剖面叠迁样式[9]。沉积模拟方面，Li 等测量了长江七弓岭段点坝的水流速度、沉积速度及沉积粒度等参数，在实验室内利用水槽实验模拟了该段点坝形成过程[10]。地下构型表征方面，岳大力等总结了曲流河点坝地下储层构型表征方法[11]；陈薪凯等利用测井相组合，识别了秦皇岛32–6 油田明下段点坝砂体[12]；Sun 等分析了沾化凹陷馆陶组点坝沉积特征，根据宽厚比将点坝分为5 类[13]。开发生产方面，李俊键等对高含水期点坝水平井挖潜适应性界限进行了研究[14]；刘卫等分析了点坝内部构型与不同井网的匹配性[15]。

综上，以往研究多是从点坝的形态、粒度、规模、水动力成因和地下构型表征方法去分析，极少考虑到点坝形成的“残缺性”，没有对残缺的“复合点坝”做定量研究和成因分析。本文选取了多种类型复合点坝演化资料，包括McMurray 复合点坝地震切片[16]、密西西比河新马德里段曲流河演化卫星影像[17]、Lageweg 等曲流河物理模拟和数值模拟资料[18-19]，通过对这些资料上复合点坝演化进行历史推演，定量各阶段点坝面积数据，分析数据规律，尝试研究其保存的“残缺性”，拟合出复合度和演化阶段的关系式。研究结论有助于分析地下复合点坝储层的内部结构和非均质性。

1 研究数据来源

由于复合点坝具有多期残缺复合性，特征复杂，对研究数据要求严苛。数据资料不仅需要反映复合点坝的构型特征、定量规模，也要反映复合点坝的演化规律。因此，本次研究从古代沉积、现代沉积及实验模拟3 个角度出发，选取特征明显、规律性强、易于测量的沉积体资料进行测量。广泛对比调研后，优选出加拿大下白垩统McMurray 组古代复合点坝地震切片[16]、密西西比河下游New Madrid现代曲流段卫星照片[17]、曲流河数值模拟[18]和物理模拟[19]资料。这4 类资料各有优缺点，将这4 类资料的拟合结果进行对比分析，可以取长补短，充分发挥各自优势，使结论具有说服力。其中，数值模拟和物理模拟资料本身就可以反映曲流河复合点坝的演化过程。古代和现代沉积则需要结合历史演化资料，才能得到复合点坝演化的过程数据。

2 复合点坝数据分析

2.1 古代沉积复合点坝数据分析

一系列等时地震切片可以反映古代沉积体的演化过程[20]。研究选取的地震切片要求资料品质高，且河道规模大。本次研究在做了调研后，选取了阿尔伯塔盆地下白垩统McMurray 组的地震切片[21]，该地震资料品质高，河道规模大，复合点坝长度在5 km 左右。在切片上，复合点坝叠置关系清楚，侧积体组合关系明晰，可以作为研究曲流河演化的资料（图1）。

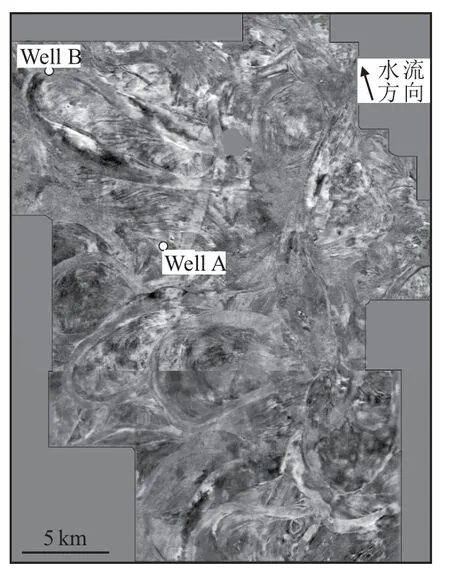
图1 阿尔伯塔盆地下白垩统McMurray 组曲流河地震切片Fig.1 Seismic slice of meandering river in early Cretaceous McMurray Formation in Alberta Basin

本次研究通过相邻层位切片对比、复合点坝叠置关系和侧积体的组合关系，恢复了McMurray 组曲流河复合点坝演化过程。具体恢复方法参考了Durkin 的曲流河演化恢复方法[22]。

一般以河道迁移两倍河道宽度为一个阶段，或者以发生如河道废弃、河道弯曲度发生较大变化等重要演化事件为一个阶段。如图2，最终恢复出复合点坝演化的12 个阶段。其中，阶段1 是最早期的河道，阶段12 是最晚期的河道。不同阶段之间河道迁移轨迹主要通过侧积体组合关系进行分析，参照切片演绎资料，同时利用弯曲度、河道宽度等参数和经验公式作为约束条件。

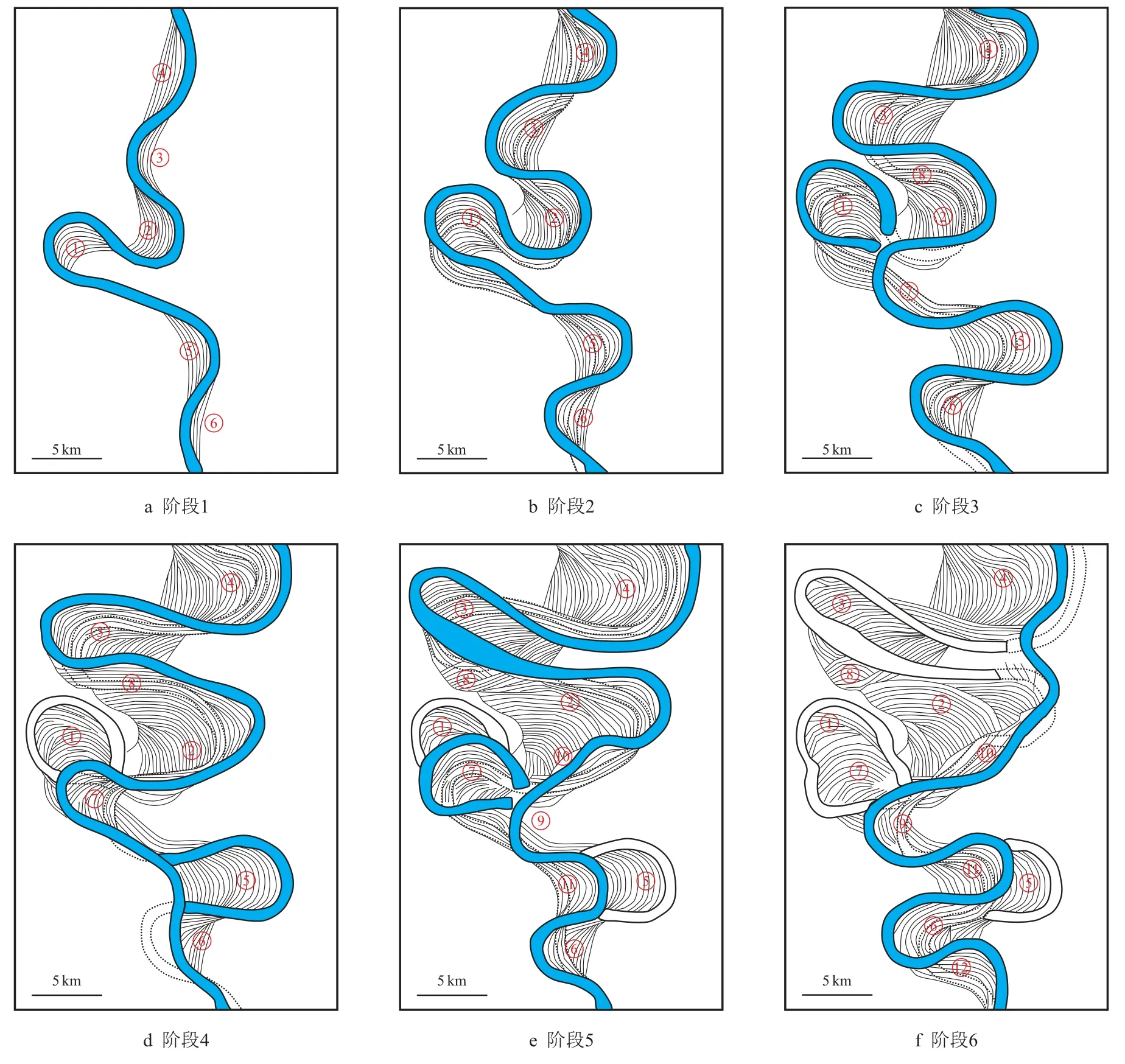
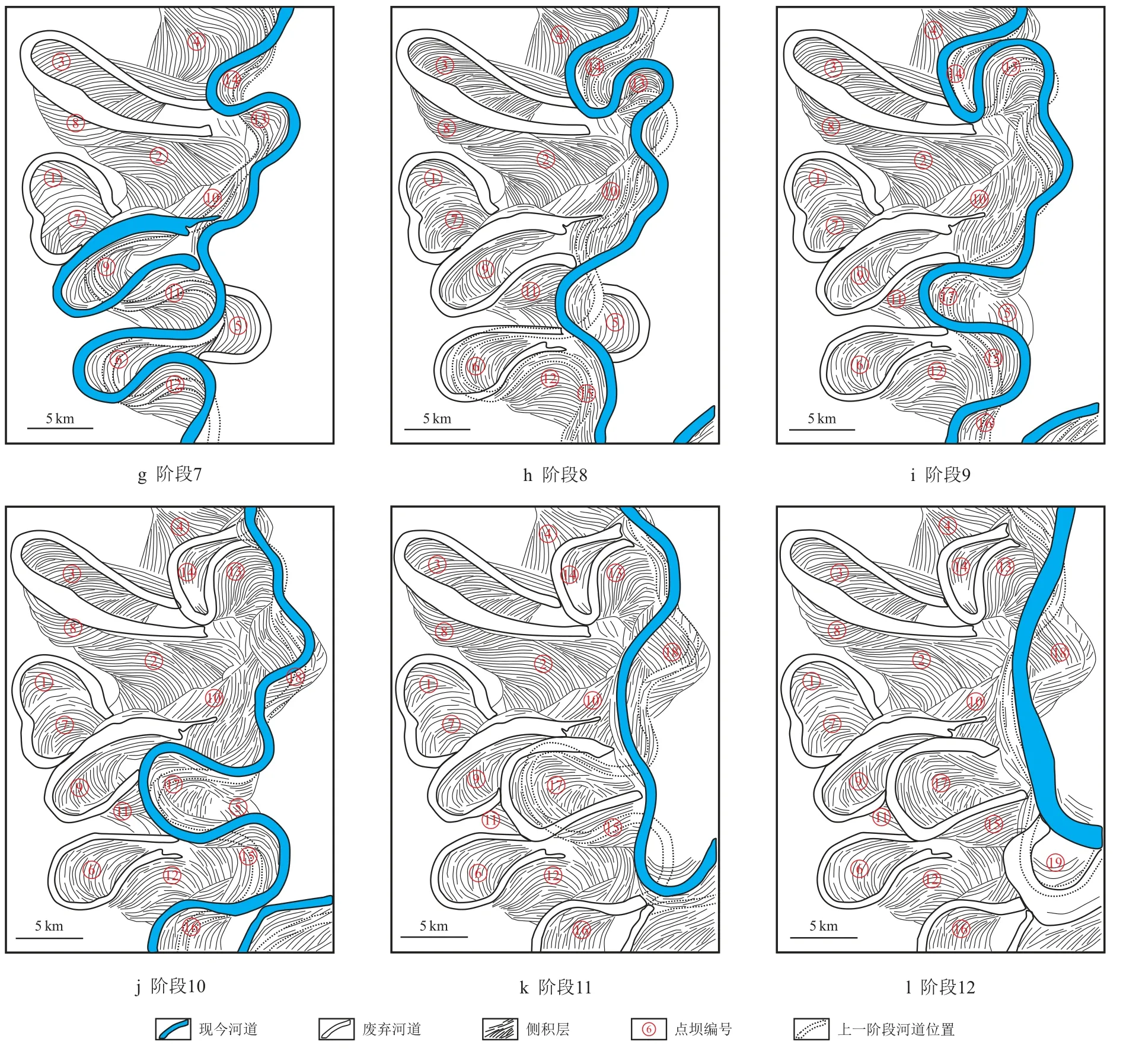
图2 McMurray 组曲流河演化恢复图Fig.2 Evolution and restoration map of meandering river of McMurray Formation

恢复过程中存在一些重要的演化节点：（1）阶段1 活动河道的弯曲度是1.68，阶段5 活动河道的弯曲度是2.52。由于点坝②、点坝③和点坝④持续侧向加积，使曲流河从阶段1 到阶段5 弯曲度快速增加。（2）从阶段2 至阶段3，点坝②反向侧积，造成点坝①对应的曲流段截弯取直，演化为废弃河道，点坝①演化为废弃点坝。（3）从阶段5 到阶段6，由于复合点坝③对应的曲流段曲颈取直，活动河道弯曲度显著降低，从阶段5 的2.52 降至阶段6 的1.94。（4）点坝①、点坝⑧、点坝⑫和点坝⑬被东部的后期点坝叠置破坏残缺。（5）从阶段10 到阶段12，曲流河弯曲度持续下降，从2.61 降至1.11，这是由于曲流段截弯取直和点坝不断向下游迁移造成的。阶段12为河道演化最终阶段，弯曲度低，点坝相互切叠复合，以砂岩充填为主。

点坝在曲流河演化的多个阶段都是变化的。曲流河侧向加积，点坝开始形成。形成初期，点坝面积小，但形态相对完整。之后，由于曲流河迁移、反向加积等作用，会破坏先期点坝，并形成新的点坝覆盖于先期点坝之上，形成复合点坝。点坝面积虽然增大，但是形态变得残缺不完整，甚至被完全破坏消失。为了便于研究点坝的演化，定义了完整点坝面积、保存点坝面积和复合度的概念。完整点坝面积是指点坝在某一阶段时未被破坏完整形态的面积；保存点坝面积是指点坝在某一阶段时破坏后保存下来的面积；复合度表示点坝在某个演化阶段时，其保存面积占完整面积的比例。由于点坝面积会增生变大，点坝演化晚期的面积一般大于早期的面积，但是复合度小于早期。具体测量点坝完整面积和保存面积时，需要参考曲流带包络形态、侧积体组合样式，同时需要参考前后演化阶段该点坝的形态。复合度可表示为

式中：y --复合度，%；s--保存点坝面积，km2；S--完整点坝面积，km2。

本次研究测量了19 个点坝在12 个阶段的完整面积和保存面积，并计算了这些点坝不同阶段的复合度，形成定量数据库。其中，点坝①～⑥在12 个阶段中均可观测到（点坝⑤在阶段12 复合度趋向于0）；点坝⑦～⑲在后期演化阶段中才出现。点坝④和点坝⑤在12 个阶段中是最连续变化的；其他点坝演化到一定阶段后，由于废弃并远离主河道，点坝形态和保存面积相对稳定，其中，点坝①和点坝③演化到阶段6 后趋于稳定不再变化，是保存稳定时期最长的点坝。点坝⑰最终保存度最高，复合度为90.18%；点坝⑤最终保存度最低，复合度为0（破坏消失）。点坝在早期阶段比晚期阶段面积小，但复合度高。阶段1，点坝总面积为18.725 km2；阶段12，点坝总面积为53.138 km2。点坝早期阶段复合度趋向于100.00%，演化到阶段12 时，平均复合度为63.72%。

以复合点坝演化阶段作为横坐标、复合度作为纵坐标，将统计数据投点至坐标轴，同时对纵轴数据制作箱型图，如图3 所示。

通过观察图3a 数据点可以发现，在点坝形成初期（1 期），复合度均为100.00%，即点坝未被破坏前是完整的。随后点坝逐渐被破坏叠置，复合度减小。有的点坝在某阶段后趋于稳定，复合度不发生变化了。整体上，复合度变化的趋势表现为先快速递减、后缓慢递减并趋于稳定，很吻合对数关系。所以用对数曲线拟合数据点，可以得到复合度与演化阶段的关系式：y=-0.1950 lnx+1，R2=0.7720。

通过观察箱型图（图3b）可以发现，随着演化阶段的增加，复合度数据的离散度增大，说明各复合点坝在形成初期，虽然破坏较大，但破坏程度是接近的，即复合度是接近的；各复合点坝在形成末期，经历了多期破坏复合，破坏程度大小不一，复合度是离散的。

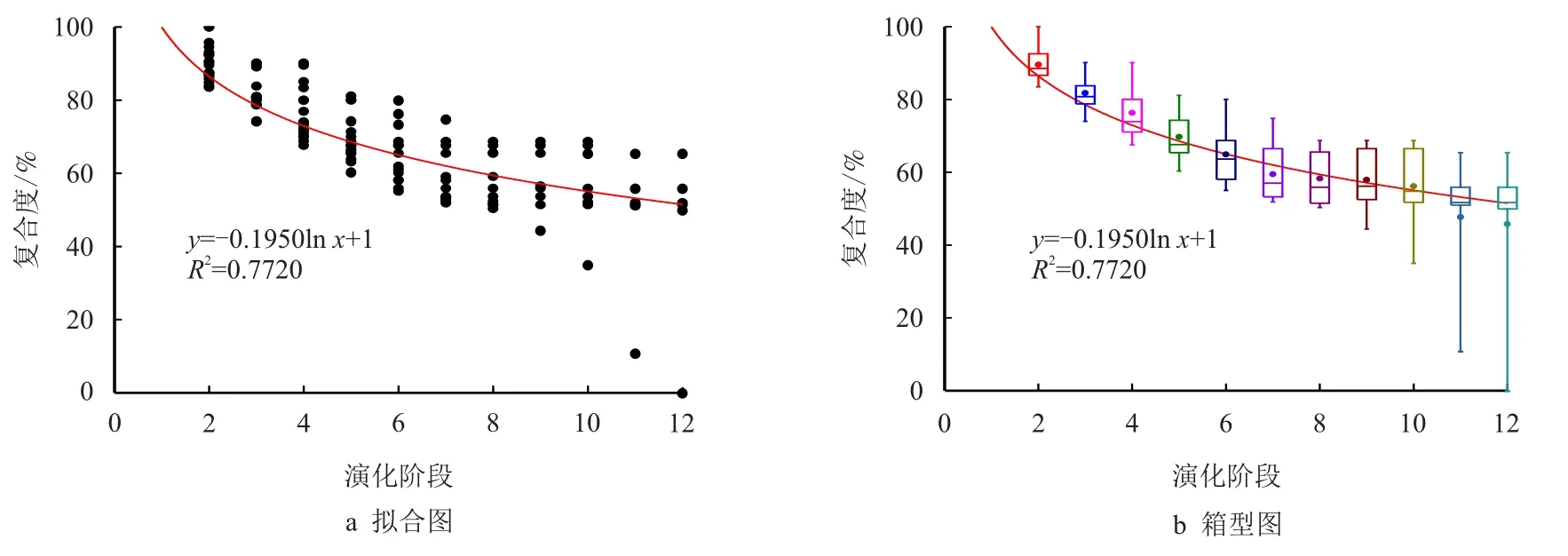
图3 McMurray 组复合点坝复合度与演化阶段拟合图及箱型图Fig.3 Fitting diagram of complex degree and evolution period of McMurray Formation composite point bars and box diagram

2.2 现代沉积复合点坝数据分析

密西西比河下游点坝发育，弯曲度高（弯曲度在1.5 以上），是典型的曲流河，且研究程度高。本次研究选取了密西西比河New Madrid 考察点（36°31′7.59′′N，89°30′44.03′′W）作为现代沉积复合点坝研究对象，进行数据统计和分析（图4）。

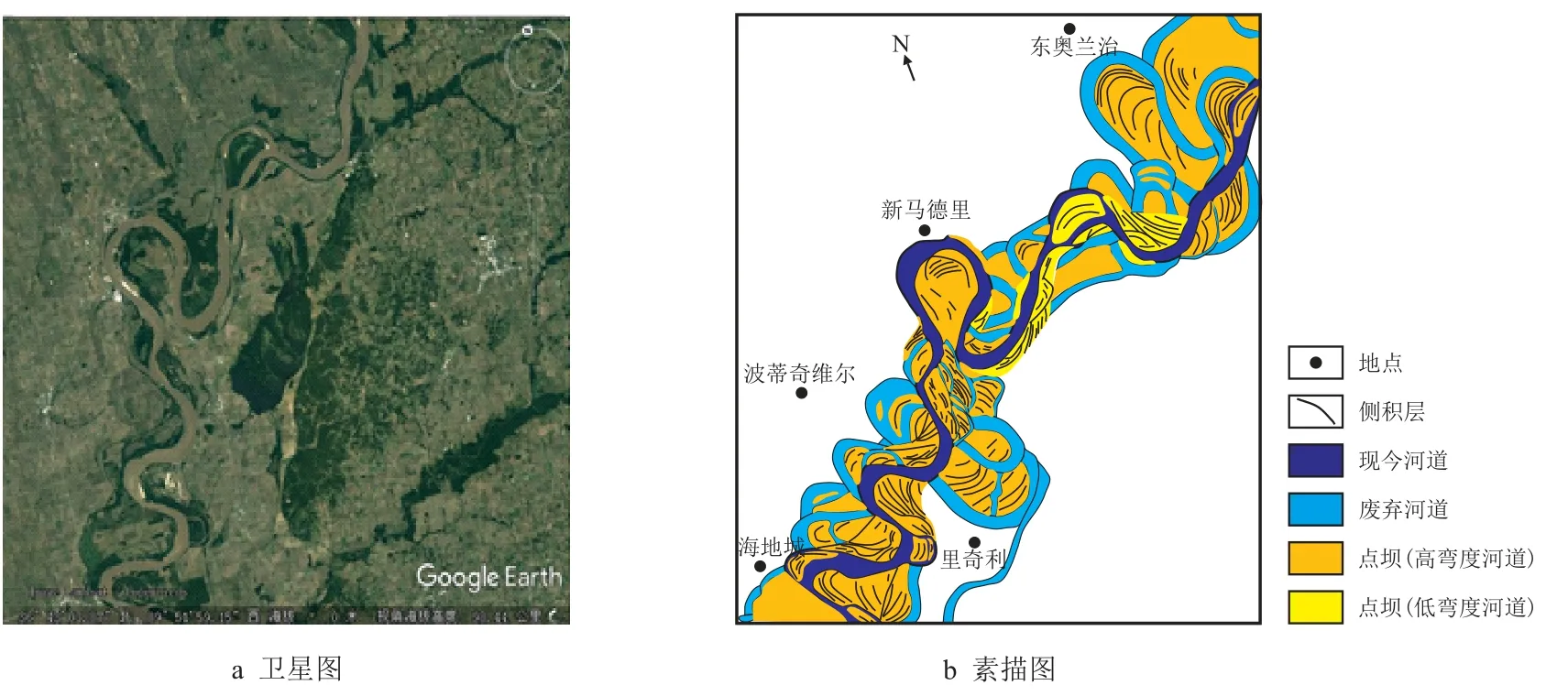
图4 密西西比河New Madrid 曲流河段卫星照片与素描图[17]Fig.4 Satellite photo and sketch of New Madrid meander section of Mississippi River

Google Earth 可以显示历年地表卫星图像。根据Google Earth 历史演化影像、文献资料等，恢复了密西西比河下游New Madrid 现代曲流段复合点坝演化过程。具体恢复过程参考了Holbrook 等的密西西比河演化图[17]和Durkin 的曲流河演化恢复方法[22]。如图5，最终恢复出复合点坝演化的9 个阶段。其中，阶段1 是最早期的河道，阶段9 是最晚期的河道，即现代河道。

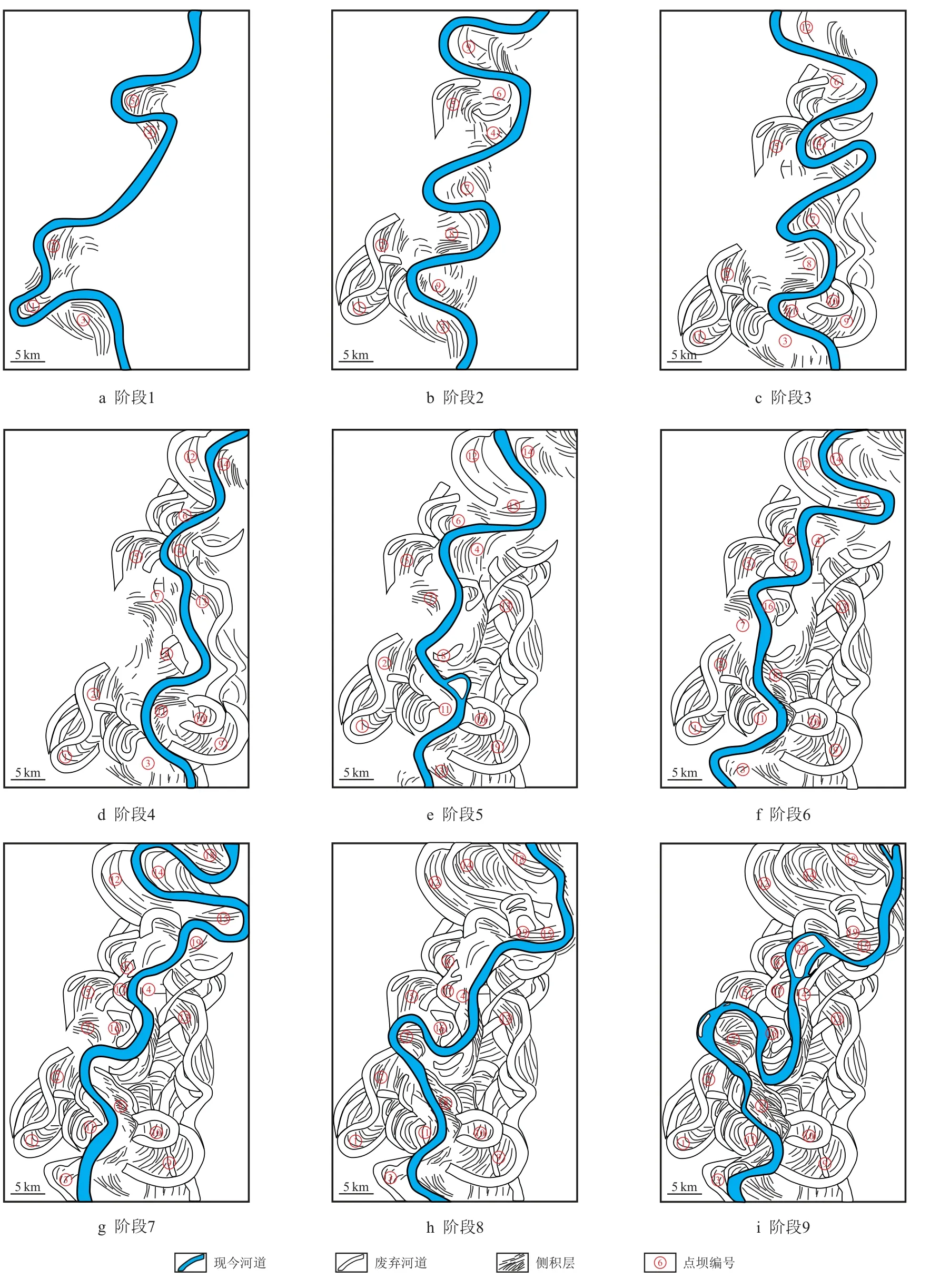
图5 密西西比河New Madrid 曲流河段演化恢复图Fig.5 Evolution and restoration map of New Madrid meander section of Mississippi River

每个阶段的节点是重要的废弃事件或活动河道弯曲度发生较大变化。重要的演化事件包括：（1）早期演化阶段的特征是曲流带横向迁移和扩张；（2）阶段1 至阶段2，点坝①、点坝②对应的曲流带发生了串沟取直，点坝①和点坝②成为废弃点坝，点坝⑤对应的曲流段发生了逆向摆动，点坝⑤成为废弃点坝；（3）阶段3 至阶段4，点坝⑦、点坝⑧对应的曲流段废弃，活动河道弯曲度降低；（4）阶段7 至阶段9，即曲流河演化晚期，河道有明显向下游迁移的趋势，点坝⑪、点坝⑮和点坝⑯均向下游加积。

本次研究测量了20 个点坝在9 个阶段的完整面积和保存面积，并计算了这些点坝不同阶段的复合度，形成定量数据库。其中，点坝①～⑤在12 个阶段中均可观测到；点坝⑥～⑳在后期演化阶段中才出现。点坝②～⑤在9 个阶段中是连续变化的；点坝①演化到阶段2 后趋于稳定不再变化，是保存稳定时期最长的点坝。点坝⑩最终保存度最高，复合度为83.22%；点坝④最终保存度最低，复合度为43.66%。点坝在早期阶段比晚期阶段面积小，但复合度高。阶段1，点坝总面积为92.95 km2；阶段9，点坝总面积为404.09 km2。点坝早期阶段复合度趋向于100.00%，演化到阶段9 时，其平均复合度为67.66%。

图6 为密西西比河New Madrid 段复合点坝复合度与演化阶段拟合图和箱型图。通过观察数据点（图6a），发现在点坝形成初期（1 期）时，复合度均为100.00%，即点坝未被破坏前是完整的。随后逐渐被破坏叠置，复合度减小。有的点坝在某阶段后趋于稳定，复合度不发生变化了。整体上，复合度变化的趋势表现为先快速递减、后缓慢递减并趋于稳定，很吻合对数关系。所以用对数曲线拟合数据点，可以得到关系复合度与演化阶段的关系式：y=-0.1830 lnx+1，R2=0.7444。通过观察箱型图（图6b）可以看出，随着演化阶段的增加，复合度数据的离散度增大。说明各复合点坝在形成初期，虽然破坏较大，但破坏程度是接近的，即复合度是接近的；各复合点坝在形成末期，经历了多期破坏复合，破坏程度大小不一，复合度是离散的。

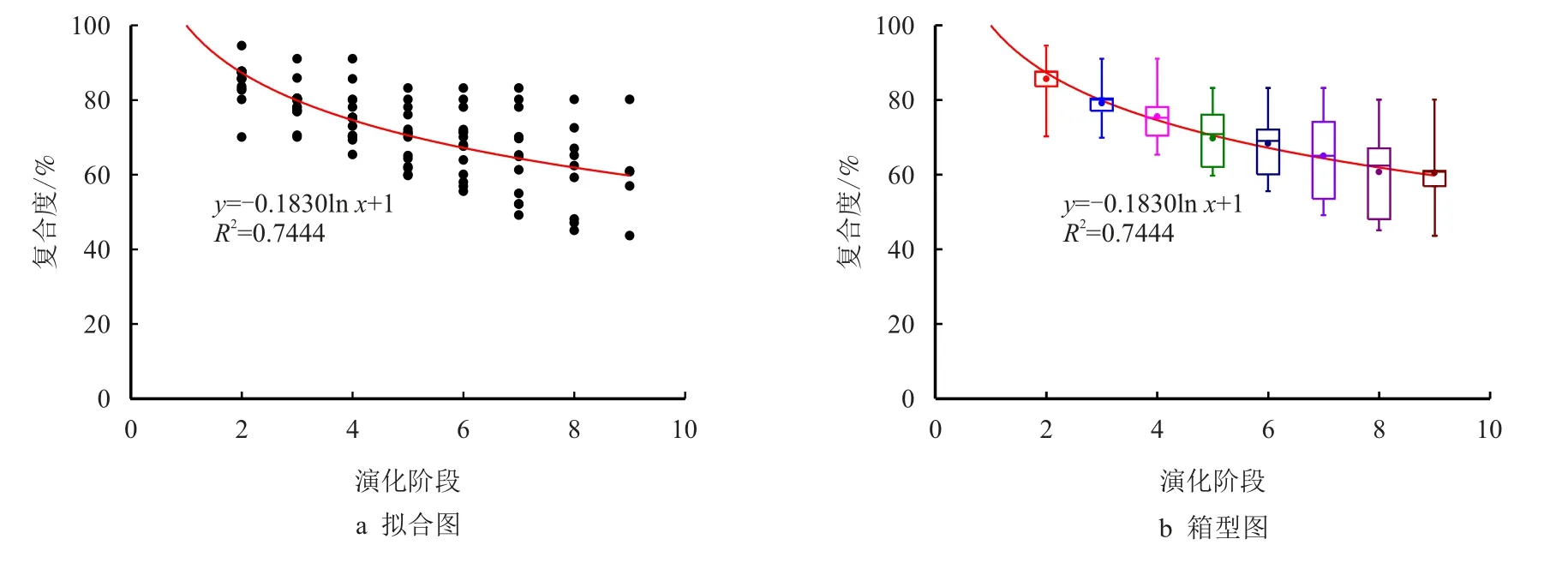
图6 密西西比河New Madrid 段复合点坝复合度与演化阶段拟合图和箱型图Fig.6 Fitting diagram of complex degree and evolution period of New Madrid composite point bars of Mississippi River and box diagram

2.3 数值模拟复合点坝数据分析

数字模拟复合点坝的数据来源于Lageweg 等采用“NAYS2D”数字模型器记录的曲流河演化过程[18]。NAYS2D 是一种基于二维流体动力学和沉积动力学模拟的数值模型，模型产生曲流河弯曲变化并不固定河岸侵蚀与加积之间的关系，允许河道在水动力条件下自由演化，更符合自然规律。模拟相关参数来源于莱茵河和密西西比河下游资料，包括河流流量、河谷坡度、沉积物粒度和泥沙淤积速率等[23-24]，此外，这两条河流也有较为详细的百年内演化历史数据[25-26]。

使用“NAYS2D”模型模拟曲流河加积弯曲的过程。模型域宽3 km，长10 km；模拟初始设置河道为一条宽200 m 的直线河道，坡度为2×10-4mm-1，沉积物平均粒度为2 mm；计算网格为20 m×20 m 的矩形。参数设置参考了Schuurman 简化后的水动力方程式[26]。

模拟运行期间，凹岸侵蚀和凸岸加积调整着河道流动轨迹。随着河道变化，网格边界不断拟合调整。通过时间步长记录沉积过程，每一个时间步长大致相当于两年河道的迁移。模型运行结束时，在坐标系中生成沉积物平面高度地貌成果图。

本次研究重点关注T=300 步长到T=1 336 步长的沉积过程，截取文献中提供的300，350，400，500，668 及1 336 步长6 个演化时间点成果图，河道演化时间范围大约相当于两千多年（图7）。

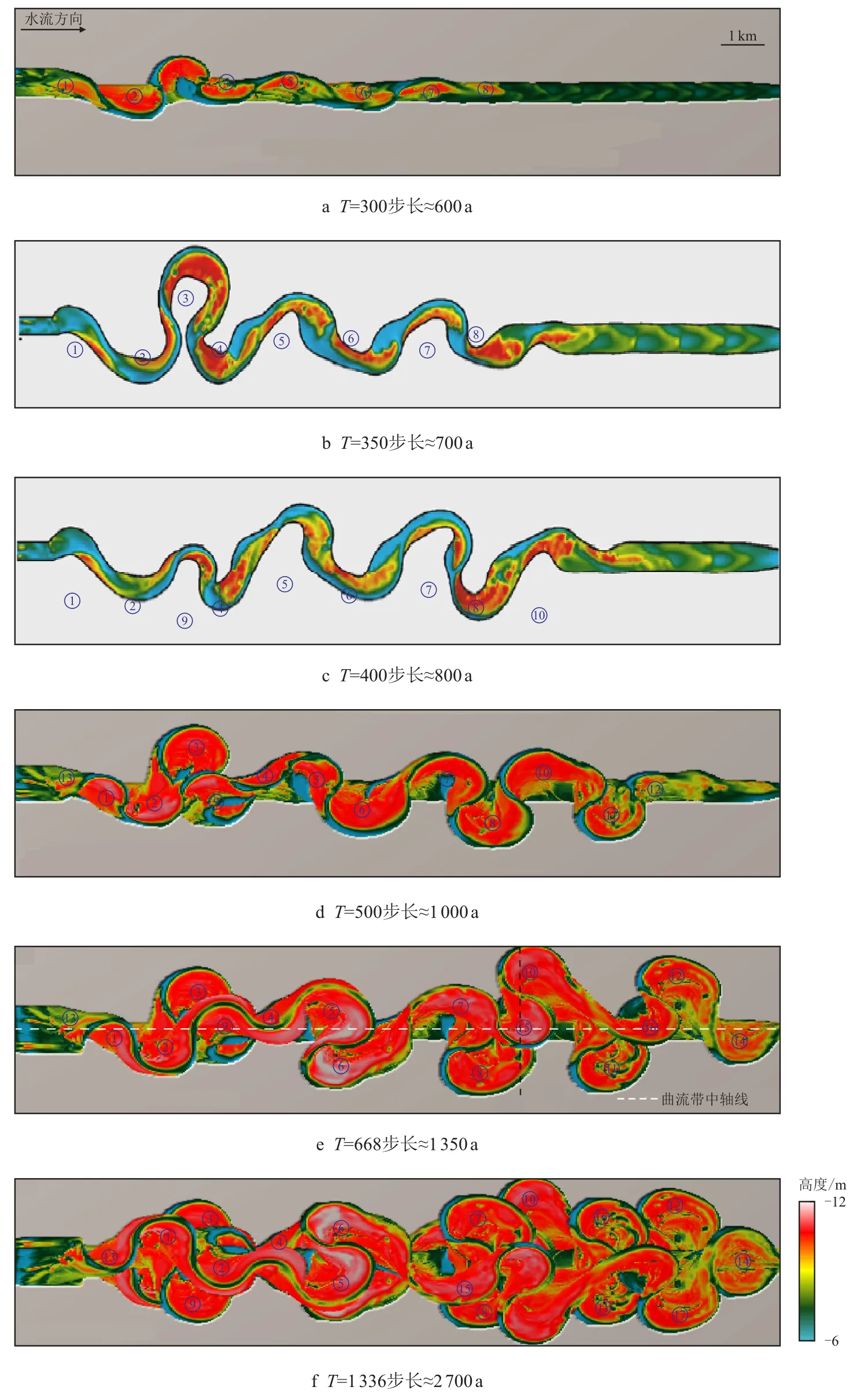
图7 NAYS2D 曲流河数值模拟模型[18]Fig.7 Numerical simulation model of NAYS2D meandering river

河道模拟至终期（T=1 336 步长）时，形成的冲积地貌长约9.0 km、宽约2.5 km，主河道弯曲度2.37，为高弯度曲流河。废弃河道和点坝相互叠置，形态复杂，列入本次数据统计的有16 个复合点坝。点坝长0.5～2.0 km，宽度大于1.0 km，废弃河道宽约150.0 m。根据横剖面数据，河道沉积厚约20.0 m。

NAYS2D 模型数值模拟成果可以直接提供曲流河的演化过程。Lageweg 等[18]提供了曲流河6 个阶段的演化成果图。阶段1（T=300 步长）是演化最早期的河道，阶段6（T=1 336 步长）是演化最晚期的河道（图7）。每个阶段河道都有一定程度的变化。重要的演化事件包括：（1）河道演化初始阶段弯曲度低，以侧向迁移作用为主；（2）复合点坝②向下游方向旋转传递迁移，导致复合点坝③被截弯取直后破坏（图7）；（3）复合点坝⑧在T=668 步长时被截弯取直，导致河道整体向下游传递加积；（4）下游点坝叠置复合程度大于上游点坝。

本次研究测量了16 个点坝在6 个阶段的完整面积和保存面积，并计算了这些点坝不同阶段的复合度，形成定量数据库。其中，点坝①～⑧在6 个阶段中均可观测到；点坝⑨～⑯在后期演化阶段中才出现。由于模拟展示的演化间隔步长，所以所有点坝在不同阶段均有变化，具有不同的复合度。具有6个阶段完整演化阶段的点坝中，点坝②最终保存度最高，复合度为82.52%；点坝⑧最终保存度最低，复合度为52.17%。点坝在早期阶段比晚期阶段面积小，但复合度高。阶段1，点坝总面积为12.4 km2；阶段6，点坝总面积为19.15 km2。点坝早期阶段复合度趋向于100.00%，演化到阶段6 时，其平均复合度为75.48%。

以演化阶段作为横坐标，复合度作为纵坐标，将统计数据投点至坐标轴，同时对纵轴数据制作箱型图件。通过观察数据点（图8a），发现在点坝形成初期（1 期）时，复合度均为100.00%，即点坝未被破坏前是完整的。随后点坝逐渐被破坏叠置，复合度减小。有的点坝在某阶段后趋于稳定，复合度不发生变化了。整体上，复合度变化的趋势表现为先快速递减、后缓慢递减并趋于稳定，很吻合对数关系。所以用对数曲线拟合数据点，可以得到关系复合度与演化阶段的关系式：y=-0.1580 lnx+1，R2=0.8003。通过箱型图（图8b），可以观察到随着演化阶段的增加，复合度数据的离散度增大。说明各复合点坝在形成初期，虽然破坏较大，但破坏程度是接近的，即复合度是接近的；各复合点坝在形成末期，经历了多期破坏复合，破坏程度大小不一，复合度是离散的。

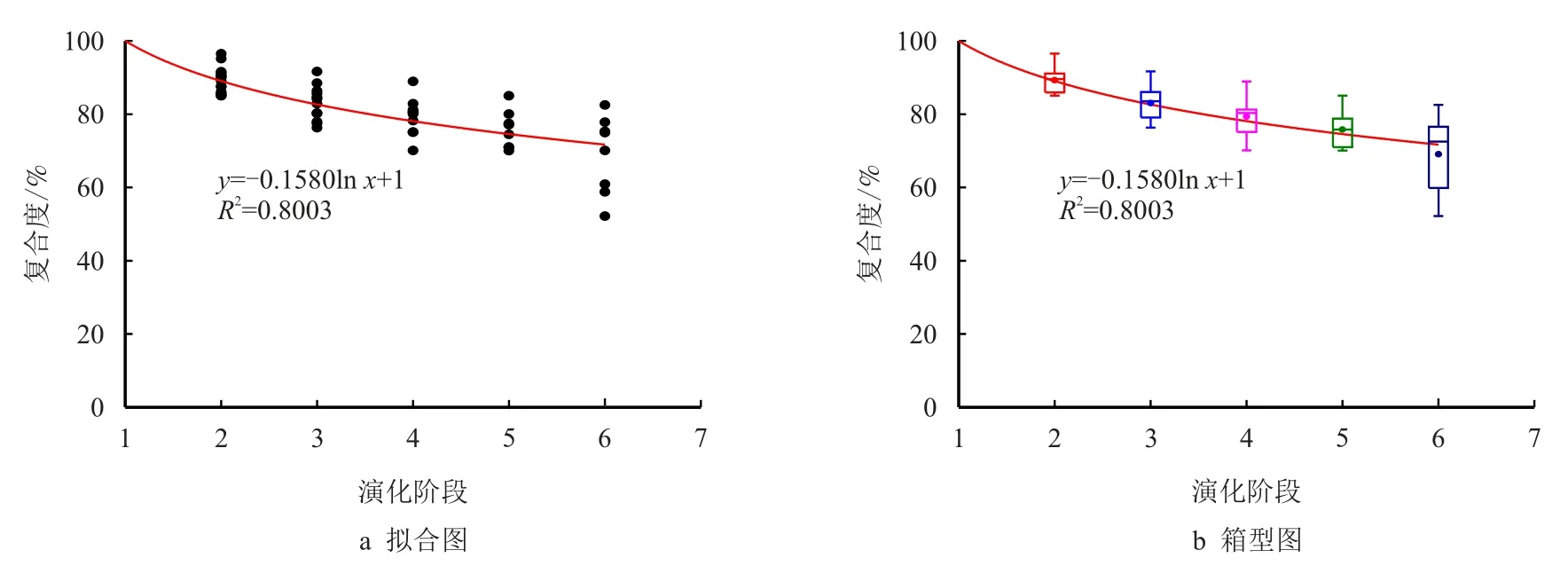
图8 曲流河数值模拟复合点坝复合度与演化阶段拟合图和箱型图Fig.8 Fitting diagram of complex degree and evolution period of numerical simulation model of NAYS2D meandering river and box diagram

2.4 物理模拟复合点坝数据分析

实验室沉积物理模拟可以辅助构建地质概念模型，通过模拟多种构造条件、多种水动力条件下的河流沉积过程，分析各构型要素空间展布规律[27]。本文物理模拟复合点坝的数据来源于Lageweg 等对砾石质曲流河的模拟实验[19]。实验装置为一个长11 m、宽6 m 的水槽，水槽坡度5.5×10-3mm-1。水槽中填充了一层厚10 cm 的差分选沉积物，在其中设计一条宽0.3 m、深0.015 m 的初始顺直河道。沉积物注入速率为1.25 kg/h，流体注入速率为11 m/s。下游边界为恒定水位的深水池，河流在深水池处形成三角洲。

物理模拟实验全过程260 h，采用垂直分辨率为0.2 mm 的激光仪记录河流地貌高度，共收集了40 组地貌高度数据，并用相机记录图像。为了获得较高的对比度，流体被染料染为紫色。关注T=0 到T=260 h 的沉积过程，截取0，30，58，128，150，171及260 h 演化时间点的成果图进行统计分析（图9）。

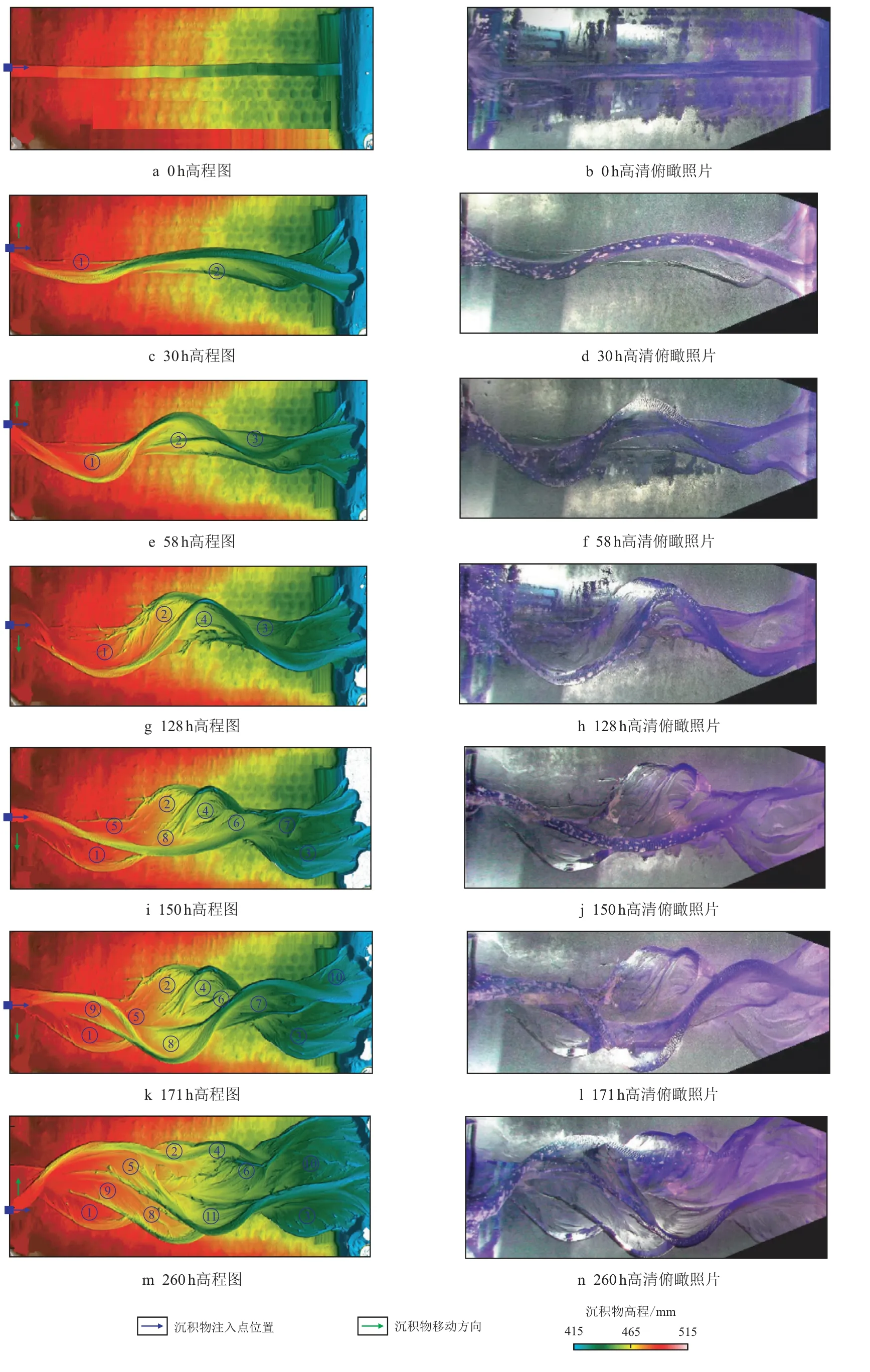
图9 曲流河物理模拟过程图[19]Fig.9 Physical simulation model of meandering river

模拟过程中，河道的规模是不断增大的。最初，河道宽度约0.6 m，流域面积约4 m2；实验结束时，河道宽度约2.1 m，流域面积约24 m2。

河道最初为设计的顺直河（图9a）。50 h 时，河道逐渐演化为低弯度曲流河，河道一侧侵蚀物提供物源，于下游相对侧形成点坝雏形，河道弯曲度增加至1.12（图9b）。随着上游沉积物不断被冲积到下游，点坝长度和宽度增加，弯曲度增加，至58 h时形成3 个点坝，河道弯曲度增加至1.30（图9c）。至128 h，出现明显点坝叠置复合现象，新形成的点坝④截断了曲流带，叠置于点坝②之上。同时，点坝内出现可以观察到的侧积体沉积，侧积体仅有几厘米宽，之间间隔具有规律性（图9d）。150 h 时，河流多个位置出现截弯取直现象，河道弯曲度迅速下降，几乎重新拉直，形成多个废弃点坝（图9e）。河道矫直后，至171 h，开始形成新的点坝，与先前点坝呈镜像关系，河道重新弯曲（图9f）。至260 h，河道演化过程大体与之前弯曲过程一致，不过由于漫滩为先期的废弃河道和点坝，后期形成的点坝多覆盖叠置于先期之上，在漫滩形成范围广泛的复杂复合点坝沉积（图9g）。

本次研究测量了10 个点坝在6 个阶段的完整面积和保存面积，并计算了这些点坝不同阶段的复合度，形成定量数据库。其中，点坝①、点坝②在6个阶段中均可观测到；点坝③～⑩在后期演化阶段中才出现。由于模拟展示的演化间隔时间长，所以所有点坝在不同阶段均有变化，具有不同的复合度。具有6 个阶段完整演化阶段的点坝中，点坝①最终保存度最高，复合度为70.50%；点坝②最终保存度最低，复合度为29.99%。点坝在早期阶段比晚期阶段面积小，但复合度高。阶段1，点坝总面积为4.93 m2；阶段6，点坝总面积为23.52 m2。点坝早期阶段复合度趋向于100.00%，演化到阶段6时，其平均复合度为68.27%。

图10 为曲流河物理模拟复合点坝演化阶段与复合度拟合图和箱型图。通过观察数据点，发现在点坝形成初期（1 期）时，复合度均为100.00%，即点坝未被破坏前是完整的。随后点坝逐渐被破坏叠置，复合度减小。有的点坝在某阶段后趋于稳定，复合度不发生变化了。整体上，复合度变化的趋势表现为先快速递减、后缓慢递减并趋于稳定，很吻合对数关系。所以，用对数曲线拟合数据点可以得到复合度与演化阶段的关系式：y=-0.2100 lnx+1，R2=0.6316。

通过箱型图（图10b）可以观察到，随着演化阶段的增加，复合度数据的离散度增大。说明各复合点坝在形成初期，虽然破坏较大，但破坏程度是接近的，即复合度是接近的；各复合点坝在形成末期，经历了多期破坏复合，破坏程度大小不一，复合度是离散的。

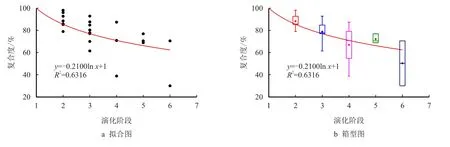
图10 曲流河物理模拟复合点坝复合度与演化阶段拟合图及箱型图Fig.10 Fitting diagram of complex degree and evolution period of numerical simulation model of meandering river

2.5 数据对比分析

由以上研究可以看出，4 种方法得到的演化阶段与复合度的拟合关系相似，其中，数值模拟数据拟合度最高，古代曲流河沉积数据（McMurray 组地震切片）和现代曲流河沉积数据（密西西比河下游段）拟合度次之（古代沉积数据略好于现代沉积数据），物理模拟数据拟合度最差。分析其原因，数值模拟采用以水动力方程为核心的计算机算法模拟曲流河演化过程，不会受到突发地质事件和人为因素的影响，故其拟合结果规律性最强，拟合度最高；古代和现代沉积反映的都是自然界实际河流，会受到突发地质事件的影响，所不同的是地震切片反映的是古代河流沉积，而卫星照片反映的是现代河流沉积（有人为因素的影响），因此，古代曲流河沉积数据拟合度略高于现代曲流河沉积数据；物理模拟法由于受到实验装置尺度、注水量和输沙量难以控制、模拟时间尺度小等因素的影响，拟合度最差。

3 复合点坝成因分析

通过以上古代复合点坝沉积（地震切片）、现代复合点坝沉积（卫星照片）、数值模拟和物理模拟等数据恢复出曲流河复合点坝演化历史，统计各演化阶段的复合度数据。在二维坐标轴投点后，都可以拟合得到一条相似的对数曲线（图11），这条曲线反映了复合点坝的成因规律，故将此曲线命名为复合度曲线。

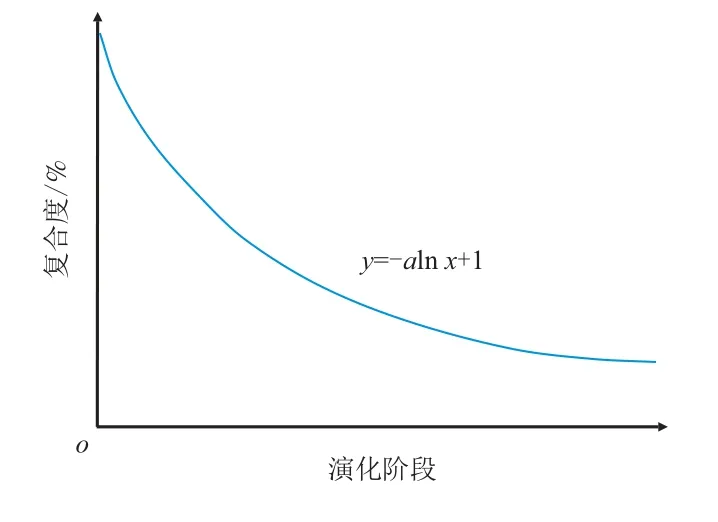
图11 复合度曲线Fig.11 Composite degree curve

复合点坝复合度与演化阶段之间普遍存在对数关系，其关系式为y=-alnx+1。关系式定义了点坝复合度为100.00%时演化阶段为1，表示点坝刚形成时形态是完整的。演化阶段增加，复合度逐渐减小，表示点坝逐渐被破坏残缺。演化阶段增加到一定程度，复合度逐渐趋于不变，表明点坝成为远离主河道的废弃点坝，形态趋于稳定。关系式与实际数据拟合度一般在0.600 0 以上，拟合度与数据来源、观测尺度及数据完整性等因素有关。不同尺度及不同观测数据都验证了这个关系式的正确性，因此，可以认为这个关系式在解释复合点坝成因时具有普遍意义，将此公式命名为复合度关系式。

复合度关系式中，系数a与河道规模、河道形态、基准面变化、水动力、地貌、植被及气候等因素有关。系数a决定了点坝的复合程度和演化速率。当系数a较小时，复合度曲线变化速率慢，说明点坝复合程度低，保存较好；当系数a较大时，复合度曲线变化速率快，说明点坝复合程度高，初期点坝不易保存，被迅速破坏甚至消失。

复合度曲线和复合度关系式揭示了复合点坝的成因规律，即：一条单一曲流河的凸岸为多期残缺的点坝组成的复合体，其中某一期点坝从形成至被破坏成残缺状态，其残缺程度（复合度）与演化阶段呈对数递减关系，最后趋于稳定或消失。复合点坝的演化规律从动态演化的角度定量分析曲流河复合点坝形成演化过程，而常规地质知识库、经验公式都是从静态角度研究。因此，对曲流河理论研究和砂体表征都具有一定的价值。

4 结论

（1）复合点坝复合度和演化阶段吻合关系式为y=-alnx+1，表示复合度与演化阶段呈对数递减关系。

（2）系数a决定了点坝的复合程度和演化速率。a较小时，点坝复合程度低，保存较好；a较大时，点坝复合程度高，初期点坝被迅速破坏甚至消失。

（3）各类数据中，古代沉积复合点坝数据拟合度最高，物理模拟复合度最低。