基于改进长短期记忆网络的短期负荷预测

王季， 李润清， 刘屾， 曹万水， 王昊，陈勇

(1.甘肃省机械科学研究院有限责任公司，甘肃 兰州 730030；2.兰州理工大学 电气工程与信息工程学院，甘肃 兰州 730050； 3.甘肃省工业过程先进控制重点实验室，甘肃 兰州 730050)

0 引 言

对于电力公司来说，减少配电网中断和电力负荷过损等问题，高精度预测是一项必不可少的工作。通常，电力负荷预测方法分为统计方法和人工智能的方法[1]。统计学方法如多元回归、自回归滑动模型和灰色预测法[2]。文献[3]研究了统计方法的模型。文献[4]介绍了长短期记忆网络(long short-term memory, LSTM)，但LSTM存在着模型复杂和训练时间久的问题。对此，文献[5]提出了一种门控循环单元(gated recurrent unit, GRU),在大部分测试中，GRU网络预测的准确性能优于LSTM网络，并且训练时间更短。单个模型往往难以获得最优的预测结果，为此文献[6]提出了一种CNN-GRU组合模型。

为了进一步提高短期负荷预测精度，本文提出了一种新的基于Attention和自相关系数的双向GRU、LSTM和卷积神经网络(convolutional neural network, CNN)的组合模型。该模型在多因素情况下最大化提高了电力系统负荷预测模型的性能。

1 CNN-LSTM-GRU模块

1.1 卷积神经网络模块

CNN主要由输入层、卷积层、ReLU层、池化层、全连接层和Softmax层构成。当处理分类任务时，把CNN输出的特征空间作为全连接层的输入，用全连接层来完成从输入到标签集的映射，即分类。一维卷积对于时间序列的特征提取输出为：

Y=σ(w·x+b)

(1)

式中：Y为提取的特征；σ为sigmoid激活函数；w为权重矩阵；x为时间序列；b为偏置向量。

1.2 LSTM模块

LSTM是一种递归神经网络结构，比传统的RNN有更好的存储和访问信息的能力。LSTM单元结构如图1所示。LSTM通过式(2)～式(5)分别确定遗忘门(ψft)、输入门(ψit)、输入节点(ψgt)和输出门(ψot)。式(6)～式(7)分别确定记忆单元在时间步长t时的状态和在时间步长t时的隐藏状态。

ψft=sigmoid(wfx+wfhht-1+bf)

(2)

ψit=sigmoid(wix+wihht-1+bi)

(3)

ψgt=tanh(wgx+wghht-1+bg)

(4)

ψot=sigmoid(wox+wohht-1+bo)

(5)

ht=tanh(st)×ψot

(6)

st=ψgt×ψit+st-1×ψft

(7)

式中:st为时间步长为t的存储单元;ht为时间步长为t的隐藏状态;w为相应的权值。

图1 LSTM单元结构

1.3 GRU模块

图2所示结构旨在解决传统RNN的不足，如消失梯度。GRU包含两个门：更新门(ψzt)和重置门(ψrt)。GRU单元在时间步长内的操作可通过以下公式表示。

ψzt=σ(wz·[ht-1,xt])

(8)

ψrt=σ(wr·[ht-1,xt])

(9)

(10)

(11)

图2 GRU单元结构

2 自相关分析与数据预处理

在此阶段，计算电力负载负荷时间序列的自相关系数。经过自相关分析和数据归一化后，将电负荷作为图像像素处理。电负荷的时间序列在输入层使用二维图像表示。

输入层必须确定电力负荷序列的长度，以用作预测框架的输入。在所提模型中，输入负载序列长度为28D,负载序列[L1,…，L28]被重新排列成二维矩阵，如式(12)所示。

(12)

2.1 特征提取阶段

使用二维卷积层提取电力负荷的重要信息，将电力负荷数据集扩展到多维特征数据集。下面给出卷积层的细节以及如何确定其内核大小。

卷积层：该模型中使用的参数为[frow，fcol，nfilter，stride]，其中frow和fcol为过滤器的行数和列数，nfilter为过滤器的数量，stride为过滤器步长的长度。frow和fcol是由使用一天和过去几天的自相关系数来决定的。

fcol={n|n=1,2,…,28:ACCn.>TH}

(13)

fcol={m+1|m≥0:ACCm×28+1>TH}

(14)

2.2 预测阶段

将二维卷积层提取的多维负荷特征作为LSTM和GRU递归层的输入。

循环层：二维卷积层的输出为4-D张量的形状与负荷相关的卷积层的输出连接起来，重构为一个三维张量。将这个三维张量应用于递归层，步骤如下所示。

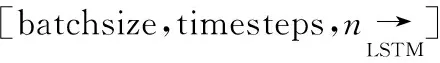
连接层1：该层连接LSTM层的输出(正向传播)和GRU层的输出(反向传播)。LSTM(反向传播)和GRU(正向传播)层：连接层1的输出同时应用为LSTM(反向传播)层和GRU层(正向传播)的输入。

连接层2：该层连接第二个LSTM层的输出(反向传播)和第二个GRU层的输出(正向传播)。

Attention层:对连接层1和连接层2的输出通过训练迭代，更新权重,输入到全连接层。

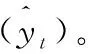
3 试验结果分析

试验利用西北某地区2006年1月1日至2007年12月30日每小时电力负荷数据集对构建的模型进行了训练。以2007年1月1日至 2007年6月30日的数据作为验证数据，以2007年7月1日至2008年12月31日的数据作为测试集。预测期为2007年7月1日至2007年7月7日。图3为从2003年12月到2014年12月西北某地区的每小时电力负荷，图4为真实值与预测值的可视化结果。

图3 西北某地区每小时的电力负荷

图4 模型真实值与预测值

该模型的性能使用二个指标进行评估。第一个指标是平均绝对百分比误差(MAPE)，第二个指标是平均绝对误差(MAE)，其定义如下：

(15)

(16)

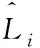
为了验证所提预测模型的可行性，将所提模型与表1所示模型进行了效果对比。相同条件下分别对测试集进行试验，根据预测结果可知，所提模型效果最佳。

如表1所示，所提模型CNN-BiLSTM-BiGRU利用式(15)和式(16)计算得出在2007年7月的MAE和MAPE中含量最低。根据表1的结果，该方法MAE的改善率优于小波神经网络(wavelet neural network, WNN),WNN+人工神经网络(artificial neural network, ANN),GRU,LSTM,LSTM-支持向量回归(support vector regression, SVR), LSTM-GRU,约为27.15%，5.4%，25.65%，20.27%，6.18%，10.32%。从试验表明，所提模型相较与其他模型具有良好的泛化能力。

表1 各模型的MAE和MAPE

4 结束语

本文分析了电力系统负荷受天气、季节、工作日、周末和节假日等多种不确定外部因素影响的问题，提出了改进的LSTM模型。分析结果表明，利用负载序列的自相关系数来确定卷积层的核大小，卷积层通过应用二维卷积核将一维特征转换为多维特征，增加了递归神经网络的预测能力。为了进一步提高短期负荷预测精度，提出了CNN-BiLSTM和BiGRU模型，再用Attention进行权重再分配，输入到全连接层进行预测，为短期负荷预测提供了新的思路。