循环荷载作用下广州软土长期累积变形特性试验研究
王 强
(中铁十一局集团有限公司,湖北 武汉 430061)
软黏土广泛分布于我国的渤海湾、长江三角洲、珠江三角洲、长江沿岸以及江浙沿海等地区,因其具有强度低、蠕变性强、灵敏度高等特点[1-2],受到工程界的广泛关注,国内外对软黏土工程地质性质的研究也越来越多。软土地区的地铁振动诱发了一系列城市岩土工程问题,根据大量工程实践资料反映,软黏土地区的地铁隧道在经过一段时间的运营后,软黏土地基将会产生较大的沉降。如林永国等[3]通过对上海地铁一号线软黏土地基的变形进行现场检测,发现地铁隧道纵向变形量过大,严重影响了地铁的安全运营;蒋军等[4]通过对长期循环荷载作用下黏土的一维沉降进行研究,发现我国京九线、京秦线等线路的粉土地基地段出现了不同程度的下沉松软、翻浆冒泥、道渣陷槽等问题;Yasuhara等[5]研究发现,日本某低路堤高速公路在投入运营后,路基的5 a沉降量达到了1~2 m[5]。由此可见,长期的循环振动荷载对软黏土地基沉降具有较大的影响。
目前国内外众多学者对软黏土动力学特性进行了大量的研究,并取得了丰硕的成果。在国外,Matsui等[6]在0.02~0.5 Hz下对塑性指数为55的软黏土进行了循环三轴试验,发现软黏土的孔隙水压力和轴向应变随循环振动次数的增加而增加,且荷载频率越低,软黏土的孔隙水压力和轴向应变越大;Monismith等[7]通过对不同应力水平下软黏土进行动力试验研究,提出了表征软黏土长期累积塑性变形与循环次数的指数模型;Li等[8]提出了修正的软黏土长期累积变形计算的Power模型;Hyodo等[9]引入相对循环应力比的概念,提出了软黏土残余应变的计算模型;Stewart等[10]则建议用半对数方程来建立软黏土长期累积塑性应变的计算模型。在国内,朱登峰等[11]根据对上海淤泥质黏土进行循环三轴试验和不排水蠕变试验的结果,分析了饱和软黏土的孔隙水压力、变形随循环周数和应力幅值变化的增长规律;Ren等[2]提出了循环荷载下饱和软黏土长期累积塑性应变的计算模型,该模型仅有3个参数,且物理意义明确、容易确定;黄茂松等[12]通过对上海地区典型饱和软黏土进行不排水循环三轴试验,分析了影响软黏土累积塑性变形的主要因素,并研究了不同静、循环动应力组合应力历史影响下软黏土的不排水循环长期累积变形特征。
由于形成环境的不同,软黏土的形成过程也会有所不同,因此软黏土具有明显的区域性。目前我国学者对宁波[13-14]、上海[14-15]、天津[16]等地软黏土的动力特性和变形方面的研究较多,而对广州地区软黏土的研究相对较少,仅有少数研究见诸报道,如匡月青等[17]对地铁列车作用下广州软黏土进行了动力响应试验研究,但是该研究未涉及到软黏土的长期塑性累积变形方面。目前,针对地铁、高铁、公路等交通振动荷载作用下广州软土长期累积变形特性方面的认识不足,特别是针对广州软土变形随循环荷载次数的变化规律和软土长期变形预测模型方面的研究还不够全面。
广州市目前有多条地铁线路穿越软土地区,比如地铁1号线、2号线、4号线、18号线等,因此研究循环荷载作用下广州软土长期累积变形特性和变形预测模型对该地区软土地铁隧道沉降变形控制至关重要。为此,本文以广州南沙地区典型的软土即淤泥质黏土和淤泥质粉质黏土为研究对象,采用室内GDS循环三轴试验仪,考虑不同土体性质和不同荷载频率两种影响因素,对广州软土进行了循环动三轴试验,研究了循环荷载作用下广州地铁隧道附近软黏土的长期累积塑性变形特性和规律。该研究成果可为广州软土地区地铁隧道在长期振动荷载作用下软黏土的变形控制提供依据。
1 循环动三轴试验
1. 1 试验土样
试验土样取自广州南沙区。南沙区位于广州市沙湾水道以南,除十八罗汉山、黄山鲁等少数丘陵地貌外,基本全区覆盖深厚软土层[18]。南沙区软土以海陆交互相软土为主,其中与地铁等人类工程密切相关的典型软土是淤泥质黏土和淤泥质粉质黏土。本次淤泥质黏土取土深度为6.3~15.7 m,淤泥质粉质黏土取土深度为18.1~26.6 m,两种试验土样的基本物理力学性质指标,见表1。

表1 试验土样的基本物理力学性质指标
1. 2 试验仪器
本试验采用英国进口的多功能动态循环三轴试验系统,如图1所示。该设备实时监控整个试验过程,高速采集并储存试验数据,是一套具有精度高、操作简单、结果可靠等优点的数字化试验设备。

图1 多功能动态循环三轴试验系统Fig.1 Multifunctional dynamic cyclic triaxial test system
该试验系统由加压系统、量测系统和控制系统三部分组成。其中,加压系统分别由3个控制器(反压控制器、围压控制器和轴压控制器)来实现,反压控制器主要用来控制试样中的孔隙水或空气,并提供反压饱和时的反压力;围压控制器主要为压力仓提供围压;轴压控制器主要用来提供轴力并控制试样的轴向变形(应变控制式和应力控制式试验均通过该泵来实现)。试样的变形、压力等数据通过传感器传至计算机处理控制系统。
1. 3 试验方案
原状饱和软黏土在天然应力条件下,应力状态处于K0固结应力条件。根据唐益群等[15]的研究成果可知,地铁列车经过时引起土体的响应频率有两个,高频一般为2.4~2.6 Hz,低频一般为0.4~0.6 Hz。因此,本次室内试验采用的两个荷载频率分别为0.5 Hz和2.5 Hz。
根据前人的研究结果[15],列车及隧道体系施加给隧道底部的附加应力在20~40 kPa之间,故本次试验采用的循环应力幅值为30 kPa。试验的最大振动次数为5 000次,当试样的应变在循环荷载次数100次以内小于0.05%即可结束试验。试验方案及控制参数见表2。

表2 试验方案及控制参数
2 试验结果与分析
2. 1 土体性质对土体循环累积变形特性的影响
图2为典型循环荷载作用下土体轴向应变随时间的变化曲线。在一次循环荷载中,土体应变可分为峰值、谷值和中值(中值为峰值和谷值的平均值),为了便于分析,以下土体的累积塑性应变量均取中值。
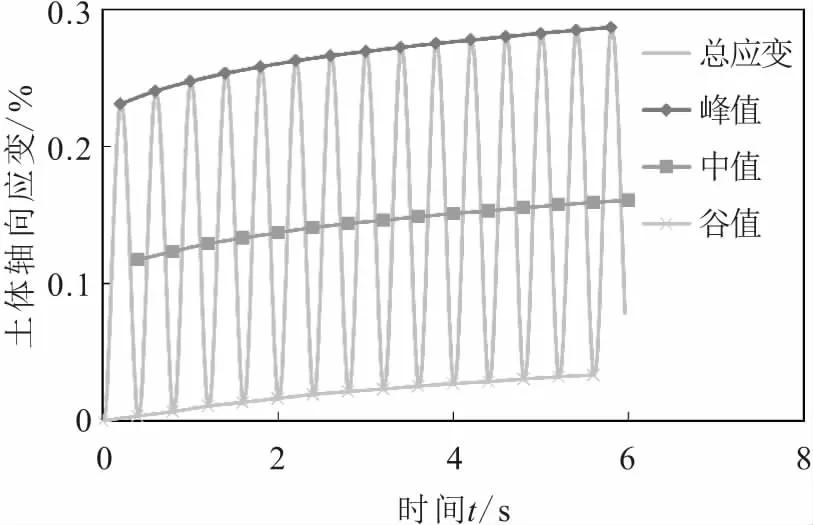
图2 循环荷载作用下土体轴向应变的峰值、中值和谷值Fig.2 Peak,median and the valley values of soil axial strain under cyclic loads
图3和图4为在荷载频率分别为2.5 Hz和0.5 Hz的循环荷载作用下淤泥质黏土和淤泥质粉质黏土的循环累积变形曲线。
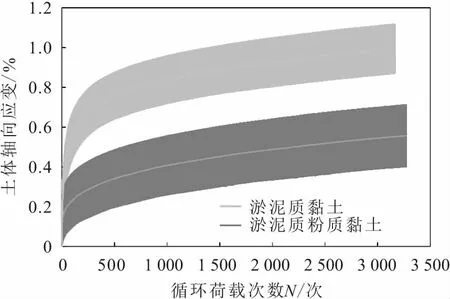
图3 荷载频率为2.5 Hz的循环荷载作用下广州软土的 循环累积变形曲线(中间曲线为土体应变中值线)Fig.3 Cyclic cumulative deformation curves of Guangzhou soft clay of soil under load frequency of 2.5 Hz (The middle yellow curve is the median strain line.)
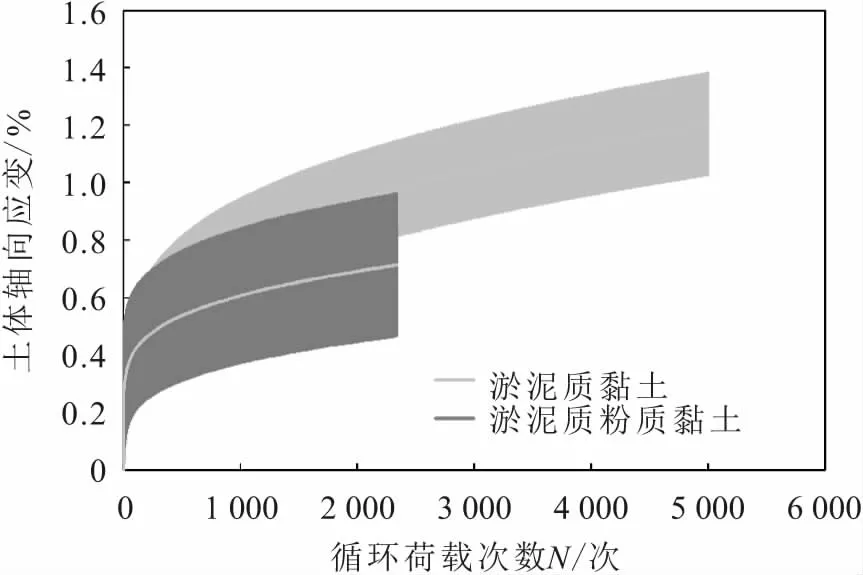
图4 荷载频率为0.5 Hz的循环荷载作用下广州软土的 循环累积变形曲线(中间曲线为应变中值线)Fig.4 Cyclic cumulative deformation curves of Guangzhou soft clay of soil under loads with frequency of 0.5 Hz (The middle yellow curve is the median strain line.)
由图3和图4可知:不论是在0.5 Hz还是在2.5 Hz的循环荷载作用下,淤泥质黏土和粉质黏土的循环累积变形曲线的变化趋势基本一致,但两种土体的累积塑性变形量明显不同,淤泥质黏土的累积塑性变形量明显大于淤泥质粉质黏土,且前者的累积塑性变形量约为后者的1.6倍。
2. 2 荷载频率对土体循环累积变形特性的影响
图5为在荷载频率为2.5 Hz和0.5 Hz的循环荷载作用下淤泥质黏土的循环累积变形曲线。
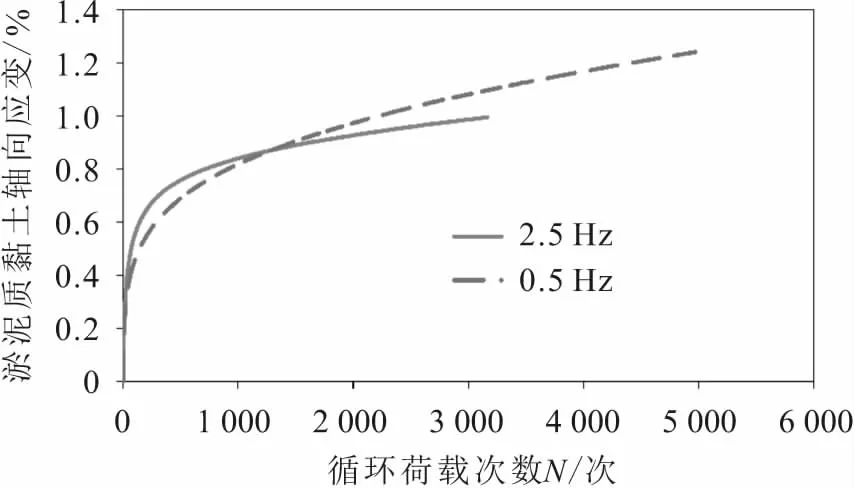
图5 荷载频率为2.5 Hz和0.5 Hz循环荷载作用下 淤泥质黏土的循环累积变形曲线Fig.5 Cyclic cumulative deformation curves of silty clay under the cyclic loads with frequency of 2.5 Hz and 0.5 Hz
由图5可知:以循环荷载次数N为1 500次为界限,1 500次之前2.5 Hz循环荷载作用下淤泥质黏土的累积塑性变形量大于0.5 Hz循环荷载作用下的淤泥质黏土,这是由于2.5 Hz循环荷载作用下的淤泥质黏土的累积塑性变形速率(即土体累积塑性应变与循环荷载次数N的比值,单位为%/次)大于0.5 Hz下的淤泥质黏土;1 500次以后2.5 Hz循环荷载作用下淤泥质黏土的累积塑性变形速率逐渐小于0.5 Hz下的淤泥质黏土,从而导致2.5 Hz循环荷载作用下的淤泥质黏土的最终累积塑性变形量小于0.5 Hz下的淤泥质黏土。
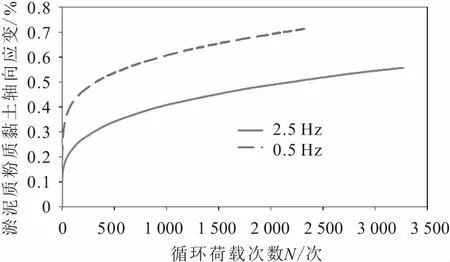
图6 荷载频率为2.5 Hz和0.5 Hz的循环荷载作用 下淤泥质粉质黏土的循环累积变形曲线Fig.6 Cyclic cumulative deformation curves of mucky silty clay under loads with frequency of 2.5 Hz and 0.5 Hz
图6为在荷载频率为2.5 Hz和0.5 Hz的循环荷载作用下淤泥质粉质黏土的循环累积变形曲线。
由图6可知:在荷载频率为0.5 Hz的循环荷载作用下的淤泥质粉质黏土的累积塑性变形速率和最终累积塑性变形量均明显高于2.5 Hz循环荷载作用下的淤泥质粉质黏土。
图7为荷载频率对广州软土累积塑性变形速率的影响。
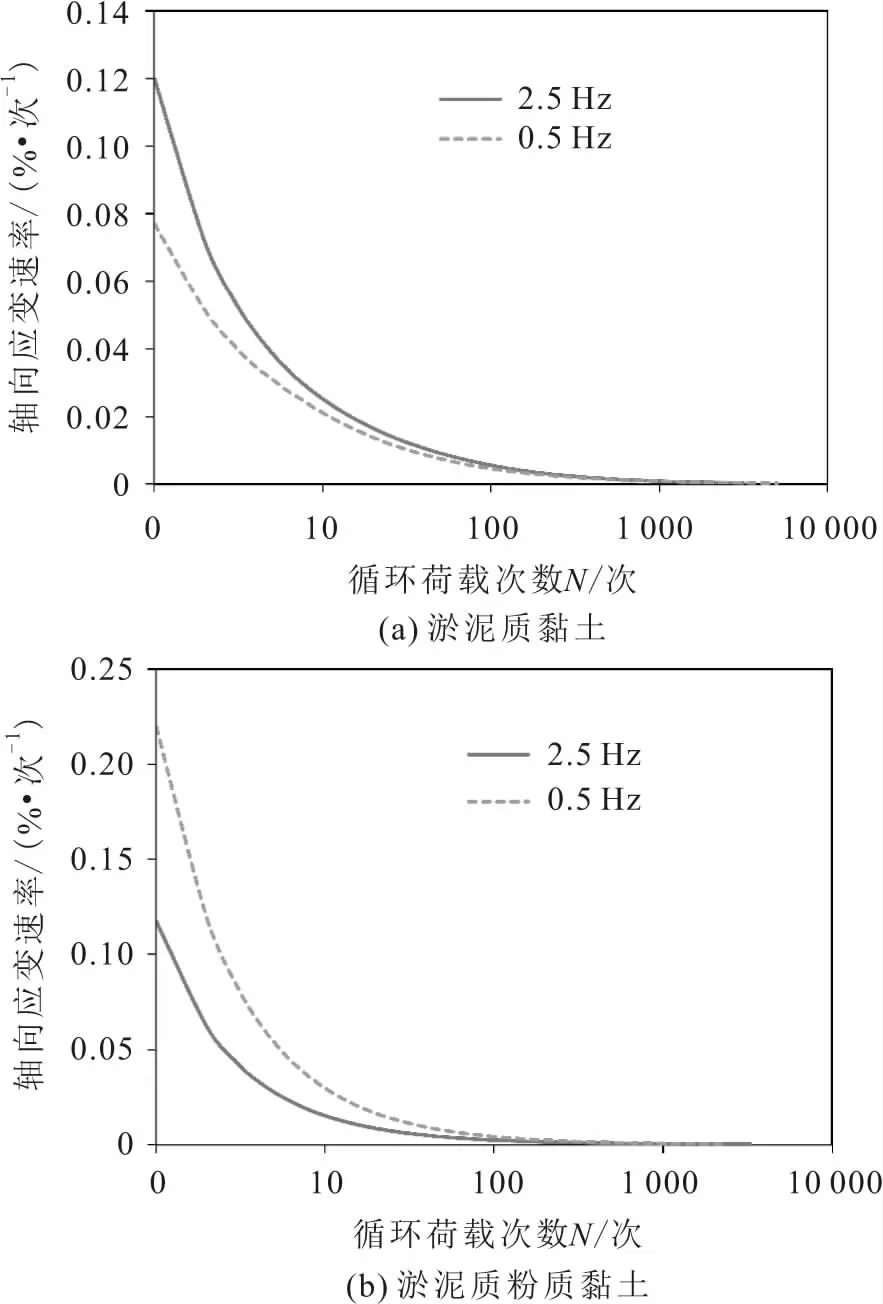
图7 荷载频率对广州软土累积塑性变形速率的影响Fig.7 Influence of frequency on accumulative plastic strain rate of Guangzhou soft clay
由图7可见:荷载频率对淤泥质黏土和淤泥质粉质黏土累积塑性变形速率的影响具有明显的不同,区别主要表现在循环荷载作用的前期(N<1 500次),对于淤泥质黏土,2.5 Hz循环荷载作用下的土体的累积塑性变形速率大于0.5 Hz下的土体,而淤泥质粉质黏土则相反。这可能是由于荷载频率对软黏土变形的影响与软土的黏滞性、敏感程度和判断标准有关,目前国内外对此尚无定论。
2. 3 软黏土的累积塑性应变计算模型
由前述可知,前人在考虑了多种因素对循环荷载作用下软黏土累积塑性变形的影响下,已经建立了许多软黏土累积塑性应变的计算模型。然而,目前使用较为广泛的是Monismith等[7]提出的经典指数模型:
εp=α·Nb
(2)
式中:εp为土体的累积塑性应变(%);N为循环荷载次数(次);a、b为模型参数。
该模型主要考虑了循环荷载次数和土体特性对土体累积塑性应变的影响。
图8给出了广州软土累积轴向应变模型计算值与实测值的对比曲线。
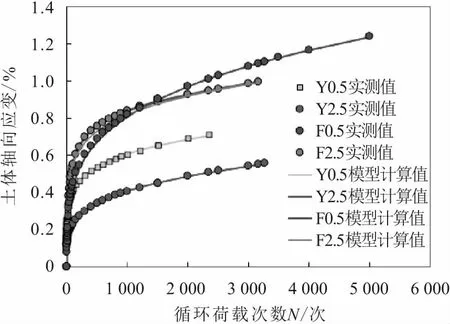
图8 广州软土累积轴向应变模型计算值与实测值 的对比曲线Fig.8 Comparison of the accumulative axial strain model of Guangzhou soft clay between calculated results and measurements注:图中Y0.5表示0.5 Hz循环荷载下淤泥质黏土的轴向应变;F0.5表示0.5 Hz循环荷载作用下淤泥质粉质黏土的轴向应变。依此类推。
由图8可知:模型拟合曲线与实测曲线完全吻合。可见,Monismith指数模型能够满足5 000次振动荷载作用下广州软土变形特性的描述和计算。
3 讨 论
由于本试验数据的缺乏,本文未考虑频率、应力历史、动偏应力等其他影响因素。本文根据Monismith指数模型所获得的模型参数仅对广州软黏土在本试验所设计的围压、反压、荷载频率、固结度、循环应力幅值等条件下才适用,不具有普遍适用性。
准确、合理的土体累积塑性应变计算模型是建立在正确的影响因素分析之上的,而影响土体动力变形特性的因素有很多,主要有土体的物理性质(含水量、液限、塑限、密度、粒径、颗粒比表面积等)、受力状态(循环动应力水平、围压、超固结比、荷载频率等)、应力路径(加载荷载波形、加载方式、试验控制方式等)等。在这些影响因素中,对于给定的土体,循环动应力水平和围压是决定土体长期累积变形最关键的因素。很多学者研究表明,土体存在临界循环应力,当循环应力水平小于临界循环应力时,无论循环荷载作用多长时间和多少次数,土体都不会发生破坏,即土体的累积塑性变形不会随着循环荷载次数的增加而一直增大,而是趋于某一稳定值;当循环应力水平大于临界循环应力时,土体会在有限的循环荷载和次数内发生破坏[1-2]。表3给出了不同黏性土的临界循环应力值。通过本文的试验结果可以发现,广州地区淤泥质黏土和淤泥质粉质黏土的临界循环应力值应大于30 kPa。
由于高铁、地铁等行车荷载在地基软土内产生的动应力实际上往往低于其临界循环应力值,因此行车荷载诱发的土体累积塑性变形在列车运营的初期会逐渐增大,但土体累积塑性变形速率逐渐减小到一定时间后土体累积塑性变形量达到最大并趋于稳定,不再随列车的运行而继续增大。Monismith指数模型的土体累积塑性应变会随着循环荷载次数的增加而持续增大,不能稳定,因此该模型描述软土长期累积变形可能是不恰当的,并且该模型参数是纯粹的经验参数,且物理意义不明确,也不能通过容易获得的土体物理力学参数而确定[2]。鉴于此,Ren等[2]在前人研究的基础上,提出了循环荷载作用下饱和软黏土累积塑性应变的双曲线计算模型,该模型仅有3个参数,且物理意义明确、容易确定。该模型可表述如下:
(3)
式中:a、b、c分别表示土体初始应变、应变率、最终累积应变。
Ren等[2]也给出了该模型中a、b、c3个参数的计算公式和取值范围,但a、c参数都与循环荷载动应力比(CSR)有关。
可见,对于广州地区的淤泥质黏土和淤泥质粉质黏土,Monismith指数模型可以描述中-短期循环荷载作用下土体的累积塑性变形,或者描述循环应力略大于临界循环应力的土体累积塑性变形。而Ren模型适用于描述循环应力小于临界循环应力的土体长期循环累积塑性变形(或者最终变形量),可应用于广州地铁等行车荷载作用下软土地基长期变形的控制与计算。
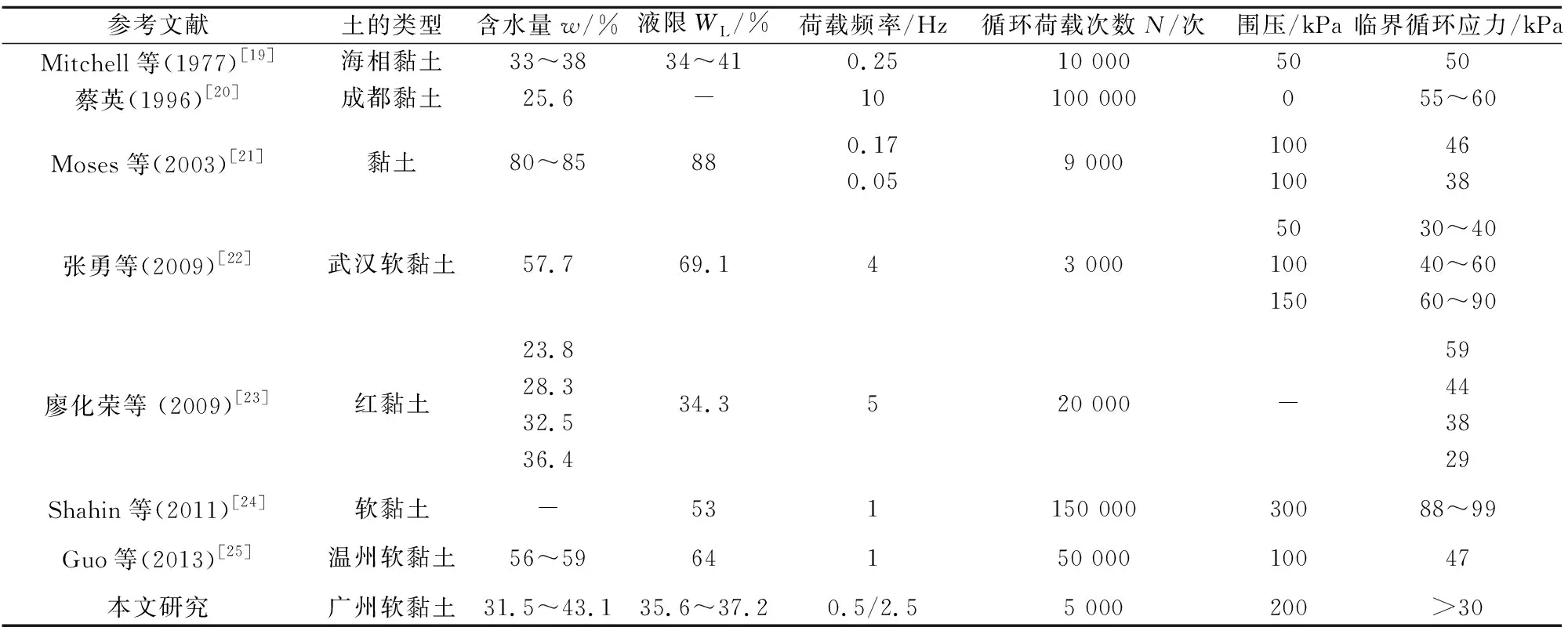
表3 不同黏性土的临界循环应力值(根据Ren等[2]修改)
4 结论与建议
本文以广州南沙区淤泥质黏土和淤泥质粉质黏土为研究对象,通过室内GDS循环三轴仪,在考虑土体性质和荷载频率两种影响因素下对广州软黏土进行了循环动三轴试验,研究了循环荷载作用下广州软黏土的累积塑性变形特性和规律,得到的主要结论如下:
(1) 土体类别和循环荷载频率对土体变形均影响显著。不论是在2.5 Hz还是在0.5 Hz的循环荷载作用下,淤泥质黏土的最终变形量显著大于淤泥质粉质黏土,且对于同一类土体,0.5 Hz循环荷载作用下土体的最终变形量大于2.5Hz下的土体。
(2) 在循环荷载应力幅值小于土体临界循环应力时,广州软土的最终变形量随时间(或循环荷载次数)的增加而逐渐趋于稳定。
(3) 广州南沙区淤泥质黏土和淤泥质粉质黏土的临界循环应力值不小于30 kPa。
(4) 分析了现有常用的土体累积塑性应变计算模型的优缺点和适用范围,并推荐给出了适合广州地铁行车荷载作用下软土地基长期变形控制与计算的模型。
需要指出的是,影响循环荷载作用下土体长期累积变形的因素很多,本文仅就土体类型(土的基本物性)和荷载频率两种因素进行了初步探索。今后拟对循环应力比、围压等重要影响因素展开研究。本研究成果是下一步工作的基础,也可为广州软土地区地铁隧道变形控制与计算提供依据。

