基于MILP模型的氢气供应链路径优化
赵 罡
国家石油天然气管网集团有限公司建设项目管理分公司
关键字:MILP模型;氢能;供应链;优化;纯氢管道;运输方式;技术经济性
0 引言
近年来,中国一直积极发展可再生能源,建造相关基础设施,以期实现国家能源可持续发展的目标、满足不断增长的能源需求[1]。作为近年来广受关注的新能源之一,氢气不仅广泛应用于煤化工、炼油、炼钢、焦化等传统工业,还涉及氢燃料电池汽车、固定式燃料电池储能等新兴产业[2-3]。从我国氢能发展趋势来看[4-5],随着工业部门脱碳需求以及氢燃料需求量的增长,氢能需求量可能会呈大幅度增长趋势。为适应氢能产业的发展,首先需要考虑实现高效、经济的氢气供应运输途径,形成区域性氢能供应网络。而当前我国各区域氢能产业发展不均衡,运输方式也较为多样化,相关情况的不确定性给氢能基础设施的规划发展和氢能供应网络的形成造成障碍。为此,综合考虑上述因素,以氢气供应链运行最小费用为目标函数,建立氢气运输路径优化模型,以期为氢气供应链系统的建设提供参考。
1 现有氢气运输方式经济性的研究
当前,氢气主要通过长管拖车(高压气氢)、管道输送(管道输氢)、液氢槽车(低温液氢)等多种方式运输[6]。相关学者[6-8]分析比较了高压气氢、管道输氢、低温液氢等不同运输方式的优缺点、适用场景和经济性。研究结果认为,单位造价最高的管道输氢方式在长距离、大规模的氢气运输中具有运输效率和成本优势。管道输氢的成本主要来源于管道初始建设投资费用,随着氢气输送量增大、管道建设成本在总成本中的比例不断降低,管道输氢的效率及成本逐渐体现出优势。当下游氢气利用程度较低时,长管拖车运输高压气氢可能是最经济的交付模式;随着下游市场规模扩大、运输距离增长[9],管道输送和液氢槽车的优势开始显现[10]。
黄宣旭等[2]通过构建氢气储运供应链成本计算方法,比较分析了不同氢气储运方式的经济性。常乐等[11]以运氢规模和运输距离为特征参数,对比分析了各种运输方式在不同情景下的成本、能耗和二氧化碳排放特性。马建新[12]定性分析了不同运输方式的成本、能源消耗安全性。目前相关研究主要是通过建立混合整数线性规划模型或混合整数非线性规划(Mixed Integer Nonlinear Programming,MINLP)模型来优化氢气供应链中的运输方式[13-16]。现有的模型[17-20]主要考虑运输方式在制氢厂至氢气需求地之间的经济性。
2 氢气供应链优化模型
2.1 模型假设
在氢气供应链的实际运行过程中,受供需双方地域分布和运输方式适用性的影响[19],氢气从制氢厂运输到需求地往往需要使用多种运输方式。由于可选择的运输方式组合类型较多,一般采用能源系统建模(特别是优化建模)方式,以最大限度地降低投资和运营成本。氢气供应链整体框架如图1所示,制氢厂在满足当地氢气消纳的同时,可以通过液氢槽车、长管拖车、天然气掺氢管道与纯氢管道运输至不同的氢气需求点。因此,只有整合各个地区的氢气资源和需求,对氢气供应链进行整体优化,保证氢气运输方式的合理性及经济性,才能使整个氢能产业产生最大的效益。

图1 氢气供应链整体框架图
氢气供应链在实际运行过程中会受到诸多复杂因素的影响,如经济因素、地理因素、运输因素等。为了方便模型的建立与求解,在不影响模型合理性与有效性的基础上作如下假设:
1)已知上游制氢厂的制氢方式和制氢单价,忽略制氢厂的建设周期。
2)只要上游制氢厂的供应能力满足下游氢气需求点的需求量,即视为氢气可销售,不考虑销售过程中的竞争关系[21]。
3)将运输情景抽象为“点对点”运输:即将制氢厂和氢气需求地均视作一个点,从制氢厂到氢气需求地之间是连接两点的直线运输[22]。
4)新建纯氢管道被假定为在现有管道旁边建造,以便能够忽略部分外协费。
2.2 目标函数
以制氢厂至氢气需求地的运输费用、氢气需求地的氢气需求量偏差费用和纯氢管道建设成本最小为目标函数,建立MILP模型。以表示制氢厂编号的集合,i表示制氢厂编号;以表示氢气需求地编号的集合,j表示氢气需求地编号;以表示运输方式编号的集合,r表示运输方式编号。目标的函数表达式为:
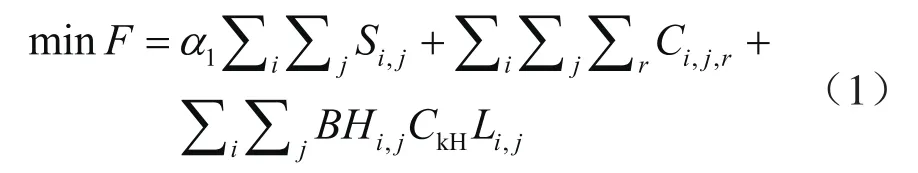
式中F表示氢气供应链运行总费用,元;α1表示未满足氢气需求量的惩罚费用,元/t;Si,j表示从第i制氢厂至第j氢气需求地的运输量与需求量的偏差,t;Ci,j,r表示第i制氢厂到第j氢气需求地采用运输方式r的运输成本,元;BHi,j表征是否建设纯氢管道的二元变量,BHi,j=1表示第i制氢厂和第j氢气需求地之间建设一条纯氢管道,BHi,j=0表示第i制氢厂和第j氢气需求地之间不需要建设一条纯氢管道;CkH表示建设一条纯氢管道的单位建设成本,元/km;Li,j表示第i制氢厂和第j氢气需求地之间的运输距离,km。
2.3 约束条件
2.3.1 氢气供应能力约束
由制氢厂向氢气需求地供应氢气的输氢量和制氢厂当地消纳的氢气量不能大于该制氢厂的生产能力,其表达式为:
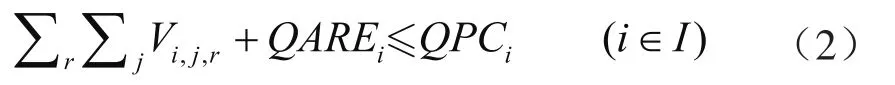
式中QAREi表示第i制氢厂的当地氢气消耗量,t/a;QPCi表示制氢厂i的氢气生产能力,t。
2.3.2 管道掺氢比例约束
将氢气掺入天然气管道的现有技术的可行性已经得到验证[23-24]。为确保天然气掺氢管道运输安全,需要严格限制管道气氢混合比,其表达式为:

式中Vi,j,2,kH表示从第i制氢厂到第j氢气需求地采用天然气掺氢管道的氢气运输量,t;Vi,j,2,kN表示从第i制氢厂到第j氢气需求地采用天然气掺氢管道的天然气运输量,t;φp表示天然气管道掺氢的最大混合比例,初设为10%。
2.3.3 运输能力约束
制氢厂只有通过被选中的运输方式才能向氢气需求地运输氢气,但选中的运输方式的运输量须满足运输方式的运输上下限,其表达式为:
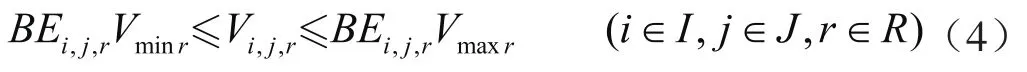
式中Vmaxr表示第r运输方式的最大运输能力,t;Vminr表示第r运输方式的最小运输能力,t;BEi,j,r表示0~1变量,如果在制氢厂i和氢气需求地j之间的运输方式r可以使用时为1,否则为0。
2.3.4 运输费用
由制氢厂至氢气需求地的运输方式考虑了天然气掺氢管道、纯氢管道、长管拖车、液氢槽车等4种运输方式。对于氢气供应链中的不同运输方式,运输距离和输送氢气重量是决定运输成本的重要参数。
其中长管拖车的总费用包含租金费用和运输费用,其表达式为:

式中Ci,j,rg表示第i制氢厂采用长管拖车运输氢气到第j氢气需求地的总运输成本,元;Ci,j,rgz表示第i制氢厂采用长管拖车运输氢气到第j氢气需求地的租金费用,元;Ci,j,rgy表示第i制氢厂采用长管拖车运输氢气到第j氢气需求地的运输费用,元;crg表示采用长管拖车的运价率,元/(t·km)。
纯氢管道运输费用的表达式为:

式中Ci,j,rhp表示第i制氢厂采用纯氢管道运输氢气到第j氢气需求地的运输成本,元;crhp表示采用纯氢管道运输方式的运价率,元/(t·km)。
其中天然气掺氢管道运输费用的表达式为:
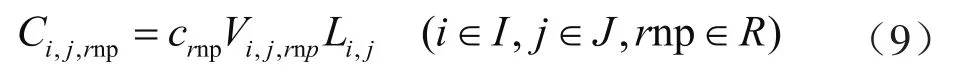
式中Ci,j,rnp表示第i制氢厂采用天然气掺氢管道运输到第j氢气需求地的运输成本,元;crnp表示采用天然气掺氢管道的运价率,元/(t·km)。
其中液氢槽车运输费用的表达式为:
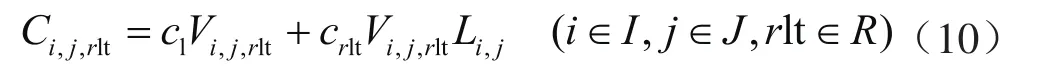
式中Ci,j,rlt表示第i制氢厂采用液氢槽车运输氢气到第j氢气需求地的运输成本,元;cl表示采用液氢槽车运输方式的液化单价,元/t;crlt表示采用液氢槽车的运价率,元/(t·km)。
2.3.5 需求偏差约束
氢气需求地从制氢厂接收氢气资源的量与偏差量总和必须等于氢气需求地的氢气需求量,其表达式为:

式中Vi,j,r表示从第i制氢厂到第j氢气需求地的运输氢气量,t;Si,j表示从第i制氢厂到第j氢气需求地的氢气的运输量与需求量的偏差,t;QREj表示第j氢气需求地的氢气需求量,t。
2.3.6 新建纯氢管道约束
纯氢管道新建的条件是其他3种运输方式的运输量不满足氢气需求地的需求量。若长管拖车、天然气掺氢管道和液氢槽车运输的氢气量小于氢气需求地的需求量,则需要新建纯氢管道;如果可以满足需求量,则不需要新建纯氢管道。其表达式如下:
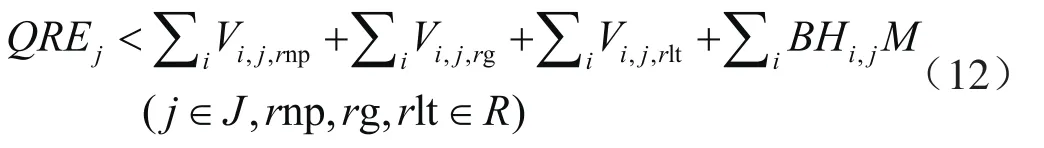
式中QREj表示氢气需求地j的氢气需求量,t;Vi,j,rnp表示第i制氢厂采用天然气掺氢管道运输至第j氢气需求地的氢气量,t;Vi,j,rg表示第i制氢厂采用长管拖车运输至第j氢气需求地的氢气量,t;Vi,j,rlt表示第i制氢厂采用液氢槽车运输至第j氢气需求地的氢气量,t;M为极大值,即尽可能大的值。
只有新建一条纯氢管道,才能由制氢厂运输氢气至氢气需求地,其表达式如下:
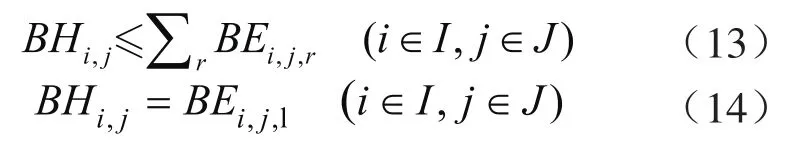
2.4 模型求解
针对本文建立的MILP模型,可直接采用Matlab中Intlinprog函数求得全局最优解。Intlinprog函数可求解的MILP问题的标准写法如下:
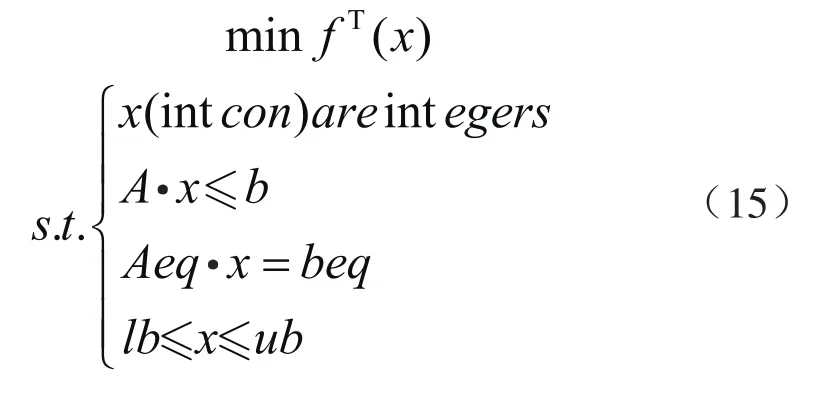
3 实际应用
3.1 基础数据
以中国南方区域的氢气供应链为研究对象,基于相关基础参数,对氢气供应链进行优化研究,求解氢气运输方案及新建纯氢管道方案。该区域制氢量及氢气需求量分布如表1所示,其中制氢厂共20个,编号为Z1~Z20(表2);氢气需求地共33个,编号为J1~J33(表3);氢气和天然气通过长管拖车、液氢槽车、天然气掺氢管道、待建纯氢管道运输(表4)。目前氢气产量的统计通常采取由下游产品产量倒推计算的方法,然而企业在实际生产过程中通常会有余量,因此产量统计数据略有差异[25]。

表1 部分区域制氢及氢气需求分布表 单位:t/a

表2 制氢厂的氢气生产能力表 单位:104 t/a
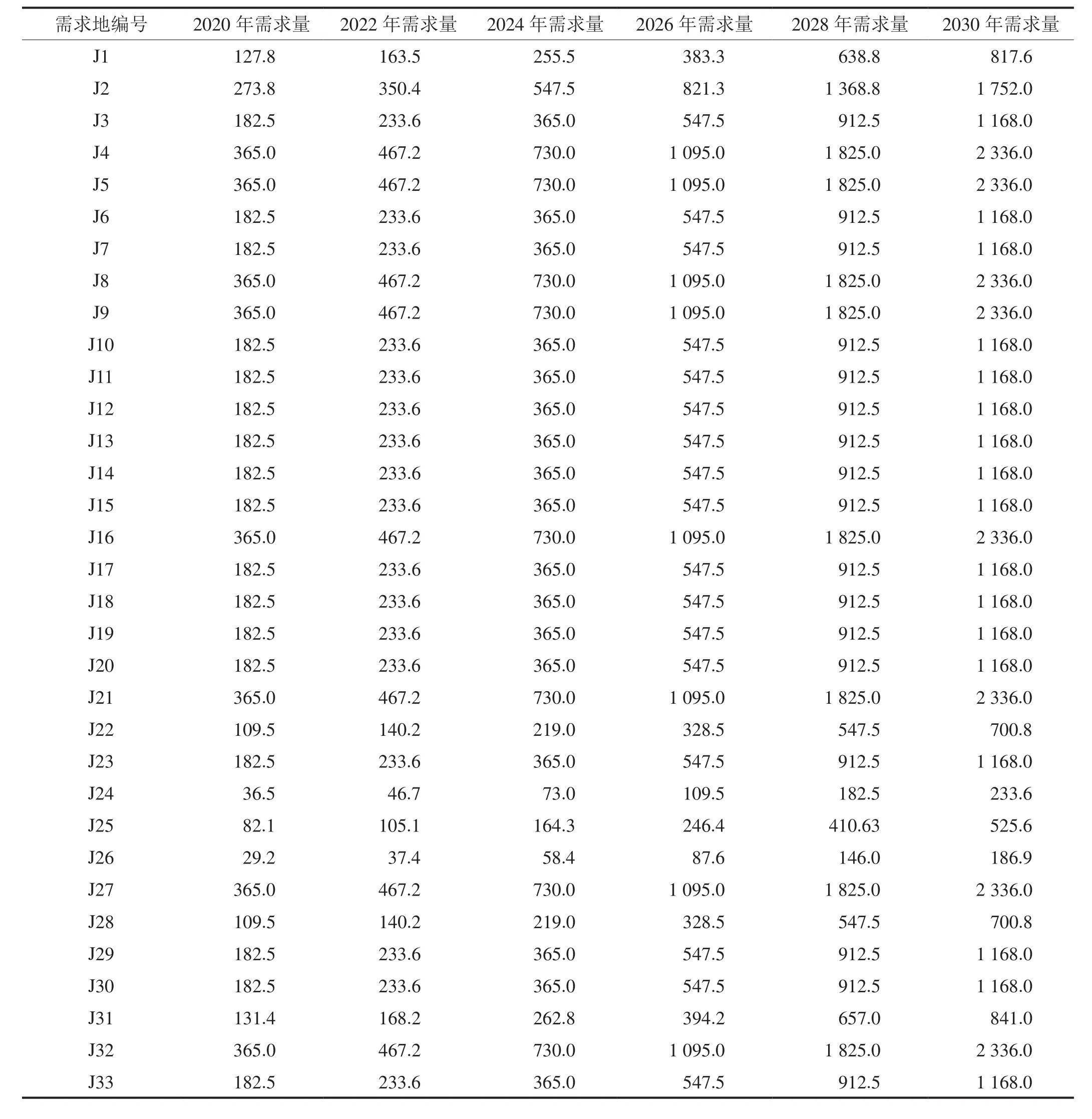
表3 氢气需求地的现有及未来预估氢气需求量表[5] 单位:t/a

表4 不同运输方式的运价率表
氢气需求量对规划氢气供应基础设施非常重要,是唯一变化的输入参数。根据《中国氢能产业发展报告2020》可知,预计2030年全国氢气需求量达3 500×104t,根据研究区域GDP占全国GDP比例估算,低情景下该区域氢气需求量约40 000 t,氢气需求地的现有及未来氢气需求量如表3所示。本次研究中氢气供应链共采用液氢槽车、长管拖车、天然气掺氢管道及新建的纯氢管道运输这4种运输方式,其运价率如表4所示。其中液氢槽车的液化氢气成本为34.29 元/kg,长管拖车的租金费用与运输距离和运输量有关,新建纯氢管道的单位建设成本为52 300元/km。
3.2 结果分析
在Matlab 2016环境下编程,该问题的连续变量、整数变量和与约束条件分别为11 881、3 299、12 626,计算用时6 s,求解得到该区域的氢气供应链优化后的运输方式选择方案(表5)。随着下游氢燃料需求的增长,采用不同运输方式的运输氢气量逐渐增加。由于氢气管道初始建设成本较高,当氢气需求量未达到2×104t之前,运输氢气量主要以长管拖车运输为主;当氢气需求量大于2×104t时,运输氢气量以纯氢管道运输为主。
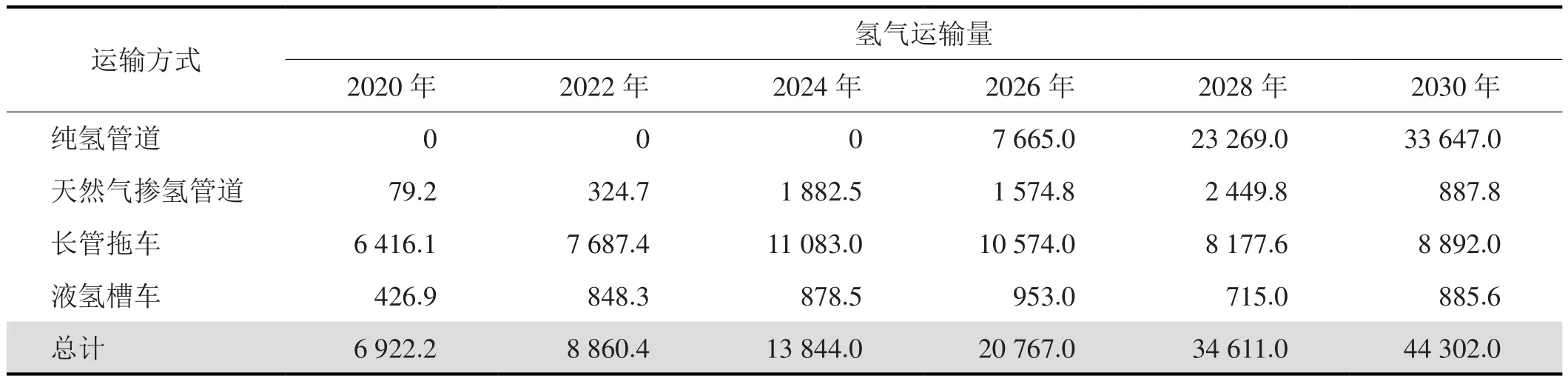
表5 氢气供应链运输方式选择方案表 单位:t
将已知条件代入模型进行求解,即可得到该区域的氢气供应链优化后的新建纯氢管道运输方案。如表6所示,在不同氢气需求量下,新建纯氢管道节段数逐渐增加,通过纯氢管道运输的氢气量也逐渐增加,同时氢气供应链的运行总成本随着氢气需求量和新建纯氢管道节段数的增加而呈增长趋势,如图2所示。

表6 研究区域的氢气供应链优化后需新建的纯氢管道运输方案表

图2 求解后不同年份的新建纯氢管道方案图
3.3 与单一输氢方式的经济性对比
通过模型求解,在未来不同氢气需求量的情景下,综合对比多种运输方式组合和单一输氢方式下的运行费用(图3)。研究结果表明,在未来不同氢气需求量的情景下,相较于单一氢气运输方式,通过模型优化所得的运输方案在考虑氢气管道规划建设的基础上组合纯氢管道运输、天然气掺氢管道运输、液氢槽车、长管拖车四种运输方式进行运输,显著降低运输成本,具有较好的经济效益,适用于未来氢气运输行业的发展。

图3 不同输氢方式的经济性对比图
综上可知,求解获得的氢气供应链方案综合考虑了输氢成本和满足氢气需求量的要求,一定程度上保证了资源的均匀分配,提升了供应链效益。
4 结论
基于纯氢管道运输、天然气掺氢管道运输、液氢槽车、长管拖车四种运输方式,考虑基础设施建设、输送流量、需求量等因素,建立以运行费用最小为目标函数的数学模型。研究结果表明,在现有氢气市场需求量的情况下,氢气通过长管拖车短距离输送、天然气管道掺氢输送是较好选择;随着未来氢气利用市场规模扩大、需求量增加,新建纯氢管道则逐渐表现出较好的经济性。研究提出的模型能够在满足氢气需求地需求量的同时保证其经济性最优,可为氢气供应链系统建设提供参考。

