复合磨损模式下的套管失效风险预测方法——以Ø193.68 mm×12.7 mm套管为例

黄文君 张星坤 高德利

中国石油大学石油工程教育部重点实验室

0 引言

在深井、超深井、大位移井等复杂油气井钻井作业中，钻柱长时间的磨损套管内壁会导致套管壁变薄甚至磨穿的情况，磨损缺陷的出现破坏了套管的完整性，导致套管的强度降低，增加了套管的失效风险。如何准确预测套管的剩余强度，并在套管设计中留有余量，是保证套管安全的关键所在。

Tamano等[1]开展了套管剩余强度实验，提出了套管在均匀载荷下极限外挤压力的经验公式。Wooley等[2]开展了套管失效的室内实验，通过测井数据来剖析套管的失效位置与失效形式，为套管的失效测试提供了依据。Adams等[3]采用数据分析方法建立了套管与油管系统定量风险分析的通用方法，为钻井工程的风险评估和确定风险最小的操作方法带来有价值的参考。以上研究为套管剩余强度的预测起到了奠基作用。美国石油学会（API）基于前人的研究，通过理论分析并开展套管破坏试验，得出一套完整套管强度的计算公式[4]，并不断地进行修订。Kuriyama[5]针对厚壁套管，提出一套新式的套管弹塑性破坏理论公式，该公式在径厚比12～24之间有足够的精度。

磨损套管强度的研究主要分为理论方法和数值模拟方法。目前的理论研究主要集中在单月牙磨损模式上，已经建立了多种模型。对于不同的模型，磨损面积的简化也不同。例如，长槽模型[6-7]将磨损区域视为矩形槽。偏心模型[8-13]假设磨损套管相当于内壁圆和外壁圆偏心的套管。等效缺陷模型[14-16]将磨损区域等同于套管的不圆度与壁厚的不均匀度。理论模型的优点是计算速度快，但理论推导中的假设和简化会导致不可忽略的误差。与理论方法相比，数值模拟方法[17-22]可以获得更精确的结果。然而，其明显的缺点是数值模拟过于耗时，尤其是在设计阶段。对于几千米深的油井，用数值模拟计算套管强度是不现实的。因此，需要建立一种兼具理论方法和数值方法优点的新方法。

1 套管复杂磨损条件

1.1 复杂磨损形状描述

钻井作业中，钻柱对套管的磨损作用会使套管的内壁形成磨损缺陷，使套管的强度降低。前人关于磨损套管剩余强度的研究大多针对单月牙磨损模式，而在实际的井下作业中，复合磨损模式也常有发生，不同的磨损模式对套管强度的影响不尽相同。图1是4类磨损模式的示意图。

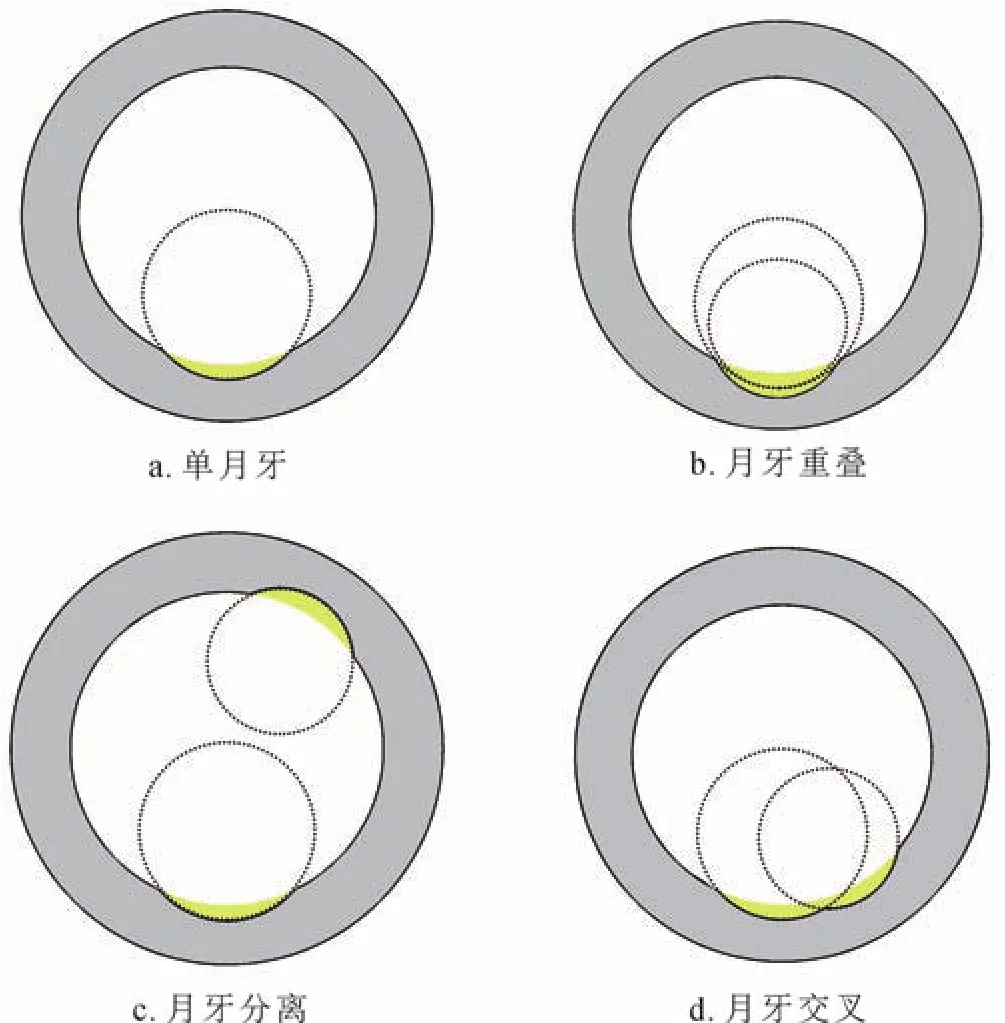
图1 不同磨损模式示意图

图1-a是传统的单月牙磨损模式，图1-b～d为复合磨损模式。图1-b是月牙重叠磨损模式，即不同直径的月牙形磨损区域在相同的位置重叠。图1-c是月牙分离磨损模式，即月牙形磨损发生在不同的位置，彼此间无交集。图1-d为月牙交叉磨损模式，即月牙形磨损的磨损位置非常接近，磨损区域相互交叉但又不完全重叠。

根据磨损形状的特点，将套管磨损模式分为4类：单月牙磨损、多月牙重叠磨损、多月牙分离磨损和多月牙交叉磨损。图1仅展示了包含两个月牙形磨损区域的复合磨损模式，而实际的磨损形状一般由多个月牙形磨损区域共同叠加形成。

1.2 套管磨损形状简化与描述

为方便计算磨损套管的剩余强度，将磨损形状进行适当的简化。通常，套管段上的磨损区域不超过两个，即使可能有3个或更多的磨损区域，也只考虑主要磨损区域和次要磨损区域，其他磨损区域相比前二者较小，可以忽略。然后，将磨损模式分为一个磨损区域和两个磨损区域。

将一个磨损区域视为近似的单月牙磨损模式，一个磨损区域可由两个参数描述：磨损深度e和磨损宽度w。磨损深度定义为磨损区域内最大磨损深度d与套管壁厚b0之比，磨损宽度定义为磨损区域圆周角θ与180°之比，如图2-a所示。这两个参数以百分数表示为：

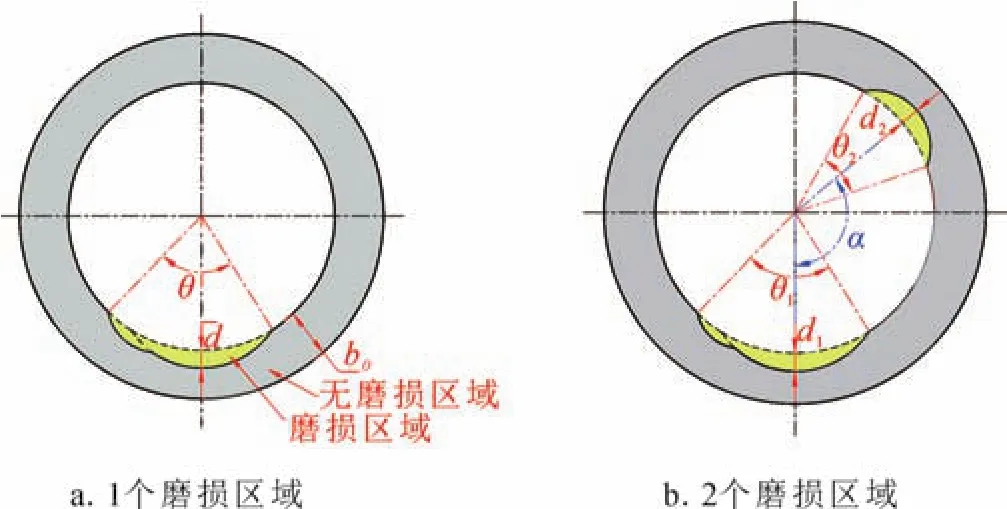
图2 套管上磨损区域示意图

对于两个磨损区域，可以将他们近似地看作两个月牙形磨损区域，即双月牙分离模式。一个是主要磨损区域，另一个是次要磨损区域。2个磨损区域可以用5个参数来描述：主磨损区域的磨损深度e1和磨损宽度w1，次磨损区域的磨损深度e2和磨损宽度w2，以及这两个区域之间的分离角α，如图2-b所示。

2 复杂磨损条件下套管失效机理与判断条件

2.1 套管内压失效

为了揭示磨损套管的失效机理，开展了一系列套管在内压作用下的失效实验。实验采用Ø193.68 mm×12.7 mm，钢级TP140V的套管，套管的磨损形式分别为无磨损、1个磨损区域与2个磨损区域。对于单一磨损区域的情形，其磨损深度与磨损宽度均为20%；对于2个磨损区域的情形，主磨损区域的磨损深度与磨损宽度均为20%，次磨损区域的磨损深度与磨损宽度均为10%。

表1给出了这3种情况下的套管内压失效的临界压力。实验结果表明，当内压增加到临界值时，套管壁会突然爆破开裂。套管内压失效是一种强度失效，失效发生在磨损最严重的部位。对于单一磨损区域的套管，在磨损区域发生开裂；对于有两个磨损区域的套管，则在主磨损区域开裂。

表1 套管抗内压强度的实验值与数值模拟计算值表

为了进一步分析套管内压失效的力学机理，开展了内压作用下磨损套管失效的数值模拟研究。选择主磨损区最大磨损深度处的径向管体，将管体由内壁向外壁等分为11个单元进行应力计算分析。对于无磨损套管，则可任选一处的径向管体。内压分别设置为从实验中获得的不同磨损套管失效的临界内压。图3为临界载荷作用下最大磨损深度处Mises应力沿着套管壁厚的分布情况。

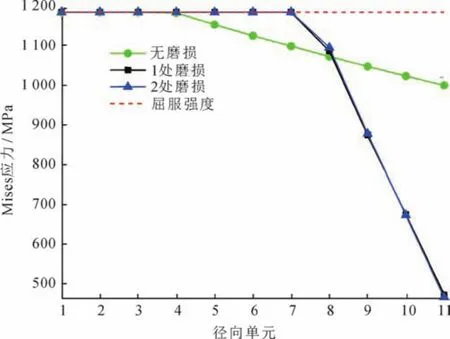
图3 临界压力下管体单元应力分布图

结果表明，当主磨损区域内管壁中部的等效应力接近材料的屈服强度时，将会发生内压失效。如果内压继续增加，主磨损区附近的套管局部变形将加速，套管破裂迅速出现。

基于上述分析可知，套管发生内压失效的临界条件为主磨损区套管壁中部的等效应力达到材料的屈服强度。采用该失效准则进行了数值模拟，并将数值结果与实验结果进行了比较，如表1所示。结果表明，数值模拟与实验结果的偏差小于4%，表明此套管内压失效准则是准确的。

2.2 套管外挤失效

与套管内压失效一样，采用同样规格与磨损形状的套管，进行了一系列外压作用下的失效实验，套管失效的临界外压值如表2所示。实验结果表明，当外压增大到一定值时，套管的椭圆变形急剧增大，并迅速被挤扁。

表2 套管抗外挤强度的实验值与数值模拟计算值表

由实验结果可知，套管的外挤失效是一种稳定性失效，套管截面形状的椭圆度是判断外挤失效是否发生的关键指标。采用数值模拟的方法计算了实验套管在外压逐渐增加过程中椭圆度的变化情况，结果如图4所示。起初，套管的椭圆度几乎不随外压的增加而变化。当椭圆度达到一临界值时，外挤压力的轻微增加会导致椭圆度急剧增加，套管被挤扁而产生外挤失效。

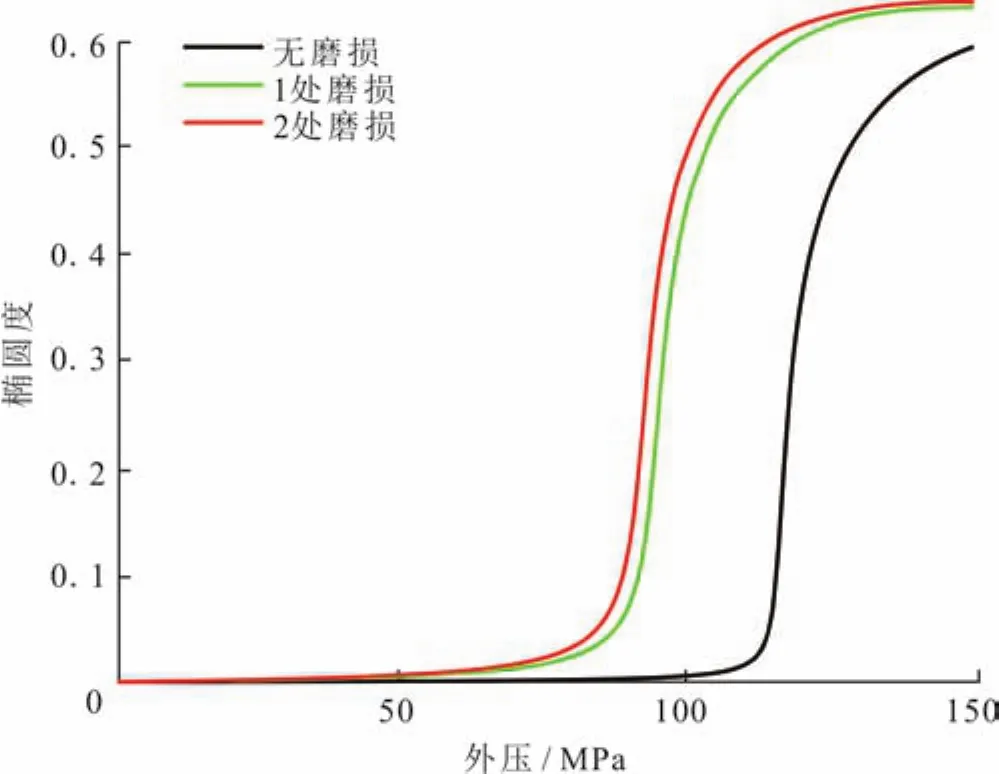
图4 不同外压作用下套管椭圆度的变化图

基于该失效准则，开展了数值模拟研究，并将数值结果与实验结果进行了比较，结果如表2所示。数值模拟结果与试验结果的误差小于3%，表明该失效准则是准确的。

3 套管剩余强度与失效风险预测方法

影响套管的剩余强度因素较多，需要通过敏感性分析明确套管剩余强度的主控因素与次要因素。根据前文建立的套管内外压失效准则，分析不同因素对套管剩余强度的影响。

3.1 套管剩余强度主控因素分析

3.1.1 单月牙磨损的影响

对于实验规格和钢级的套管，关键参数包括外径193.68 mm，壁厚12.7 mm，屈服强度1 160 MPa，添加一处月牙形磨损。分析磨损深度时，保持磨损宽度为40%，仅改变磨损深度；分析磨损宽度时，保持磨损深度为20%，仅改变磨损宽度。它们对剩余强度的影响如表3所示。

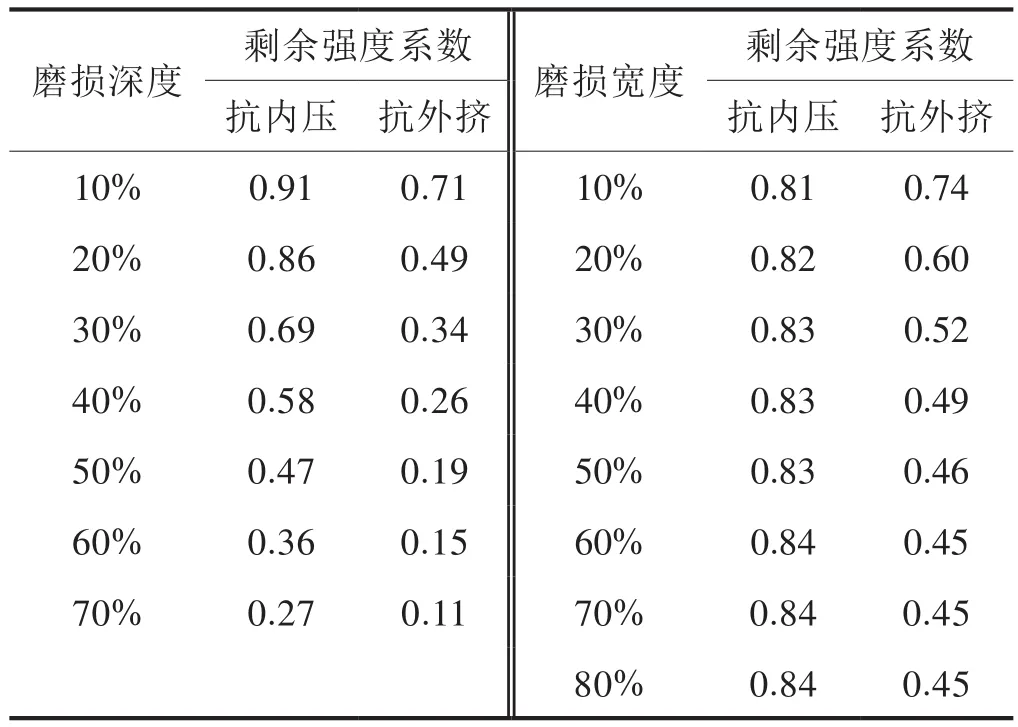
表3 单月牙磨损对剩余强度系数的影响表

为在同一标准下比较磨损对套管内压与外挤强度的影响，对剩余强度进行无量纲处理，下同。剩余强度采用剩余强度系数的形式，即：

式中k表示剩余强度系数，无因次；pw、p0分别表示磨损套管、未磨损套管的剩余强度，MPa，未磨损套管强度通常由生产厂家或API公式计算得到。

随着磨损深度的增加，套管的抗外挤强度和内压强度都在显著降低，磨损深度从10%升高至70%，抗内压强度降低了70.55%，抗外挤强度降低了83.84%；随着磨损宽度的增加，套管的抗内压强度略有增加，抗外挤强度随之降低。磨损宽度从10%升高至80%，抗内压强度升高了2.74%，抗外挤强度降低了37.86%。

3.1.2 双月牙分离磨损对剩余内压强度的影响

对实验规格和钢级的套管，添加两处月牙形磨损，保持一处磨损的深度为20%，宽度为10%，第二处的磨损宽度为10%不变，改变第二处的磨损深度与两处磨损的夹角，其对抗内压强度的影响如图5所示。

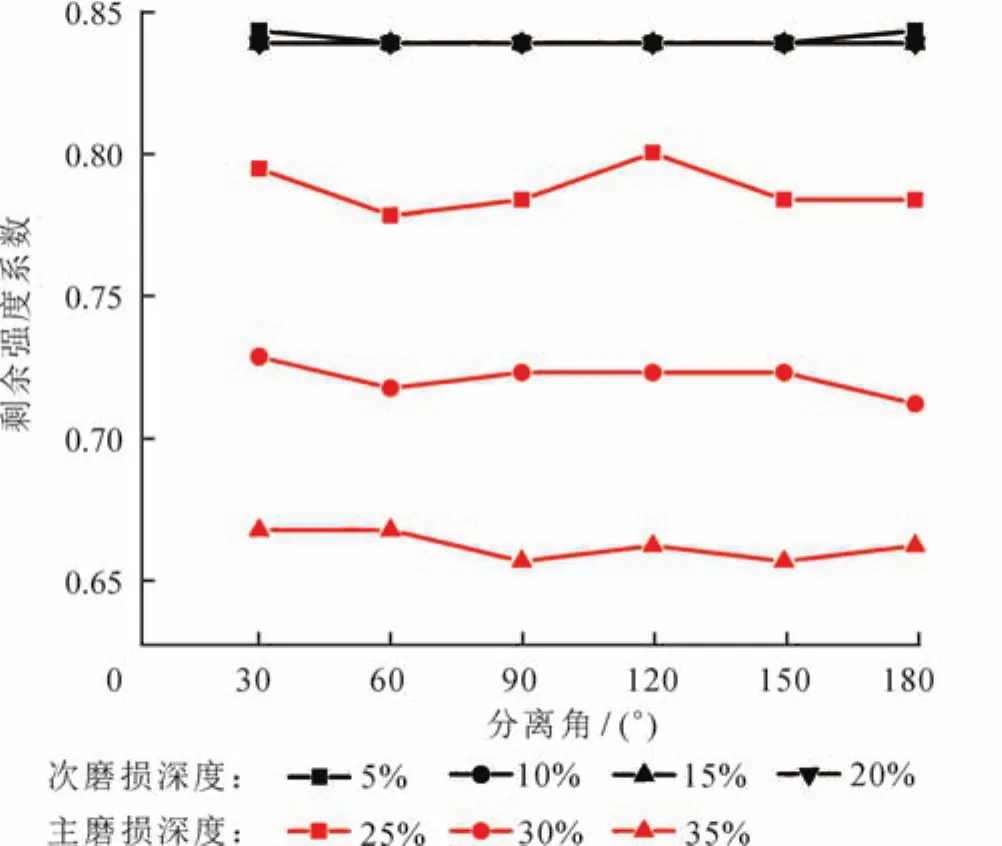
图5 磨损深度和分离角对剩余内压强度的影响图

由图5可知，磨损缺陷之间的分离角对套管的抗内压强度影响较小，7组不同的磨损缺陷组合，夹角从30°到180°，抗内压强度最大变化2.85%；次磨损深度增大5%，抗内压强度平均减小0.007 5%，次磨损深度的增加对抗内压强度影响很小；主磨损深度增大5%，抗内压强度平均减小8.35%，主磨损深度的增加对抗内压强度影响较大。由于磨损宽度对抗内压强度影响很小，故不再分析一处磨损宽度改变对剩余强度的影响。

3.1.3 双月牙分离磨损对剩余外挤强度的影响

3.1.3.1 改变一处的磨损深度

对实验规格和钢级的套管，添加两处月牙形磨损，保持一处磨损的深度为20%，宽度为10%，第二处的磨损宽度为10%不变，改变第二处的磨损深度与两处磨损的夹角，其对抗外挤强度的影响如图6所示。

图6 磨损深度和分离角对剩余外挤强度的影响图

由图6可知，对于同一组磨损缺陷组合，抗外挤强度在90°夹角附近最大，在两侧逐渐减小，两处磨损的缺陷大小越相近，夹角对外挤强度的影响越显著；次磨损深度增大5%，抗外挤强度平均减小0.83%，次磨损深度的增加对抗外挤强度的影响较小；主磨损深度增大5%，抗外挤强度平均减小14.37%，主磨损深度的增加对抗外挤强度的影响较大。

3.1.3.2 改变一处的磨损宽度

对实验规格和钢级的套管，添加两处月牙形磨损，保持一处磨损的深度为20%，宽度为20%，第二处的磨损深度为20%不变，改变第二处的磨损宽度与两处磨损的夹角，其对抗外挤强度的影响如图7所示。

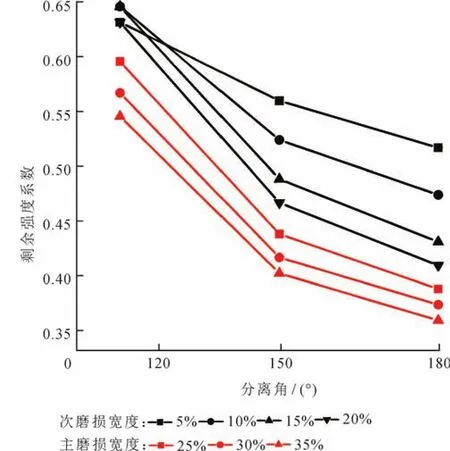
图7 磨损宽度和分离角对剩余外挤强度的影响图

由图7可知，主磨损宽度的增加对剩余强度的影响大于次磨损；次磨损宽度增大5%，抗外挤强度平均减小4.08%；主磨损宽度增大5%，抗外挤强度平均减小4.12%。

3.1.4 径厚比和屈服强度的影响

分析径厚比时，套管的屈服强度设为800 MPa不变，仅改变套管的径厚比，有磨损套管添加一处磨损深度、宽度均为20%的磨损缺陷；分析屈服强度时，对于实验规格的套管，仅改变材料的屈服强度，有磨损的套管分析时，添加一处月牙形磨损，保持磨损深度宽度均为20%。

随着径厚比的增加，套管的抗内压与抗外挤强度逐渐降低。径厚比从15升高至21，无磨损套管抗内压强度、抗外挤强度分别降低了27.20%和62.07%；磨损套管抗内压强度、抗外挤强度分别降低了31.07%和58.82%。

当屈服强度从500 MPa增加到1 200 MPa时，非磨损套管的剩余抗内压强度与剩余抗外挤强度分别增加了113.75%和82.86%；磨损套管的剩余抗内压强度与剩余抗外挤强度分别增加了138.71%和59.62%。随着屈服强度的增加，套管的剩余抗内压强度与剩余抗外挤强度都大幅度增加。

3.2 套管剩余强度的智能预测模型

虽然数值模拟可计算套管的剩余强度，但每次计算都需要重新建模，计算耗时长，可移植性差。为解决该问题，本节建立了套管剩余强度智能预测模型。首先，通过有限元软件的二次开发，获得了大量不同规格、钢级和磨损形式的套管剩余强度。其次，考虑套管剩余强度的主控因素，建立了套管剩余强度的神经网络预测模型。最后，将神经网络模型的预测结果、实验测试结果与数值模拟结果进行了横向对比，分析了智能模型的预测精度。

套管剩余强度预测问题的神经网络结构共包含三层：输入层、隐藏层和输出层。输入层为套管剩余强度的主控因素，隐藏层包含10个节点，输出层为套管剩余强度。

3.2.1 数值仿真方案

3.2.1.1 抗内压强度的计算

影响套管剩余抗内压强度的因素包括径厚比、屈服强度、磨损深度、磨损宽度和分离角。其中，磨损宽度和分离角对套管剩余强度的影响不大，为便于后续计算，将磨损宽度和分离角分别设置为40%和180°。因此，仅需要考虑不同的径厚比（15～25，5个位级）、材料屈服强度（500～1 200 MPa，5个位级）、磨损深度（主磨损深度0～80%，次磨损深度0～80%，均为9个位级）的组合，共有1 125组抗内压强度的计算结果。

3.2.1.2 抗外挤强度的计算

影响套管剩余抗外挤强度的因素包括径厚比、屈服强度、磨损深度、磨损宽度和分离角。当分离角为180°时，套管的剩余抗外挤强度最小，为了保守起见，分离角度设置为180°。仅需要考虑不同的径厚比（15～25，3个位级）、材料屈服强度（500～1 200 MPa，3个位级）、磨损深度（主磨损深度0～75%，次磨损深度0～75%，均为6个位级）、磨损宽度（主磨损宽度0～75%，次磨损宽度0～75%，均为6个位级）的组合，共有3 159组抗外挤强度的计算结果。

3.2.2 神经网络模型结果

数值模拟结果中，80%用作训练集，15%用作验证集，5%用作测试集，采用Levenberg-Marquardt算法对神经网络进行训练。

3.2.2.1 训练结果

在回归图中，横坐标表示数值模拟的结果值，纵坐标表示神经网络模型的结果，回归线的角度约为45°，内压和外挤模型对应的相关系数分别为0.998 76和0.994 17，如图8所示，表明神经网络模型在训练集和验证集上有较好的拟合效果。

图8 模型训练结果回归图

3.2.2.2 神经网络模型的测试结果

神经网络模型的训练效果良好，但其泛化能力仍需进一步的测试。因此，选择了约100组未经训练的数据，对神经网络模型进行泛化能力测试。结果表明，回归线的角度约为45°，内压和外挤与对应的相关系数分别为0.966 3和0.966 3，泛化能力良好。

对于规格为Ø193.68 mm×12.7 mm、钢级为TP140V的套管，对比了实验测试、数值模拟和神经网络模型的剩余强度结果，如表4所示。数值模拟和神经网络模型的精度均大于90%。因此，神经网络模型是可靠的，可以用来计算套管的剩余强度。

表4 套管剩余强度结果对比表

3.3 套管失效风险预测

磨损套管剩余强度的计算公式由式（3）转化为：

套管抗内压与抗外挤强度计算时不仅要考虑套管尺寸、材料、磨损形状等因素，还要计入套管的轴向力的影响。通常而言，套管上的轴向力为轴向拉力，轴向拉力会提高套管的抗内压强度，但是会减小套管的抗外挤强度。因此，套管抗外挤强度要考虑轴向力的影响，而抗内压强度则不考虑。考虑轴向力影响的套管强度计算公式为：

式中p0'表示无磨损套管存在轴向力时的外挤或内压强度，MPa；ka表示修正系数，无因次。

关于修正系数ka的计算，目前主要有3类方法：Bull5c3模型[4]、Tamano模型[1]与 OCTG 模型[14]。将这3种模型计算结果与数值模拟结果进行了对比，如图9所示。结果表明，当套管的径厚比逐渐增大时，修正系数ka也不断增大。因此，当套管的径厚比越大时，套管越容易被挤毁，轴向力对外挤强度的影响反而越小。相关研究表明[23]，当套管的径厚比增大到某一值时，套管的外挤破坏进入到弹性失稳区，此时套管轴向力不会影响套管外挤强度，这与数值模拟的认识一致。

图9 不同模型初始强度下降系数随径厚比的变化图

由图9可知，相较于数值模拟结果，Tamano模型进入弹性失稳区过早，Bull5c3模型在弹性失稳区中轴向力的影响过大，OCTG模型在弹性失稳区与数值模拟结果较为接近。通过综合对比，选择OCTG模型来计算修正系数ka，最大误差不超过6.4%。

利用OCTG模型计算式（5）中修正系数ka得到p0'，再将式（4）中的p0换成式（5）的p0'，即可得到综合考虑套管磨损和轴向力影响的剩余强度p'w。

为保障井下作业的安全性，可采用安全系数的方法来预测套管的失效风险。我国规定了套管设计的安全系数，抗外挤安全系数So=1.0；抗内压安全系数Si=1.1。因此，校核套管的安全性时，应保证实际的安全系数大于或等于规定值：

式中S'表示实际的安全系数，无因次；p表示套管实际的外载，即内压或外挤压力，MPa；S表示允许的安全系数，无因次，So=1.0，Si=1.1。

4 案例分析

以我国西北部某超深井X为例，进行套管失效风险预测。X井的测深为8 270 m，六开井身结构，一开井眼尺寸为660.4 mm，井深601.86 m，完钻后下入Ø508 mm套管固井；二开井眼尺寸为444.5 mm，井深4 123.3 m，完钻后下入Ø365.13 mm套管固井；三开井眼尺寸为333.38 mm，井深6 431 m，完钻后下入Ø273.1 mm套管固井；四开井眼尺寸为241.3 mm，井深7 180 m，完钻后下入Ø206.4 mm+Ø193.7 mm套管至井深7 179.47 m固井；五开井眼尺寸为165.1 mm，井深7 777 m，完钻后下入Ø139.7 mm套管固井，悬挂井段6 870～7 777 m；六开井眼尺寸为120.65 mm，井深8 270 m，裸眼完成。

五开钻进过程中，四开套管内壁产生磨损；六开钻进过程中，四开套管和五开尾管内壁都产生磨损。鉴于四开套管和五开尾管的磨损问题最突出，且是整个井筒完整性的关键屏障之一，因此是本节的主要研究对象。

X井六开完钻后，采用60臂井径测量仪器对套管内径进行了测量。由于受限于井下高温高压条件以及测量仪器的工作性能，只获取到了井深4 575 m以内的测量数据。可通过套管磨损预测模型[24]计算井深4 575 m以外的套管的磨损量，再结合4 575 m以内的测量数据得到整口井套管的磨损量，如图10所示；最后，采用套管失效风险预测方法计算整口井的套管强度与最大工作载荷。

图10 最大磨损深度的测量与计算图

利用磨损套管剩余强度的智能预测模型结合套管的失效风险预测方法，考虑磨损与轴向力作用，计算套管剩余强度，如图11所示，并给出了最大工作载荷。磨损包括无磨损、考虑主磨损区域、考虑全部磨损区域。无磨损无轴向力表示既不考虑套管的磨损也不考虑轴向力对剩余强度的影响。

图11 套管的剩余强度图

结果表明：忽略磨损与轴向力作用的套管剩余强度会明显大于考虑磨损与轴向力作用套管的剩余强度。抗内压强度主要由主磨损区域决定，次磨损区域对套管抗内压强度的影响可忽略不计；主磨损和次磨损对套管的抗外挤强度均有较为明显的影响，因此两个磨损区域都不能忽略。套管的轴向力一般为轴向拉力，轴向拉力的存在会减小套管的抗外挤强度，在计算套管的抗外挤强度时，不能忽略轴向力的作用。

由套管抗内压强度结果可知，最危险的井段位于0 m和7 000 m井深附近，因为该井深附近的套管磨损严重，导致套管抗内压强度最小，抗内压强度最小值约为63.0 MPa。根据套管失效风险预测方法，应使套管的实际安全系数大于或等于规定的抗内压安全系数Si，由式（5）计算，安全内压值最大为57.3 MPa。因此，后续生产过程中井筒压力要小于57.3 MPa。如果不考虑套管磨损的影响，则6 000 m井深附近无磨损套管的抗内压强度最低，为最危险井段，该结论与实际情况不符。

由套管抗外挤强度结果可知，最危险的井段位于井深0 m、4 500 m和7 000 m附近。0 m井深附近套管的轴向力最大，导致套管的抗外挤强度较小；4 500 m和7 000 m井深附近的套管磨损严重，导致套管的抗外挤强度大幅度降低，在7 000 m井深附近达到最小值18.3 MPa。根据套管失效风险预测方法，由式（6）计算，安全外挤值最大为18.3 MPa。如果忽略套管磨损的影响，则井底为套管外挤失效最危险的位置，该结论与实际情况不符。

表5为考虑轴向力套管磨损后的抗内压和抗外挤强度的降低幅度。

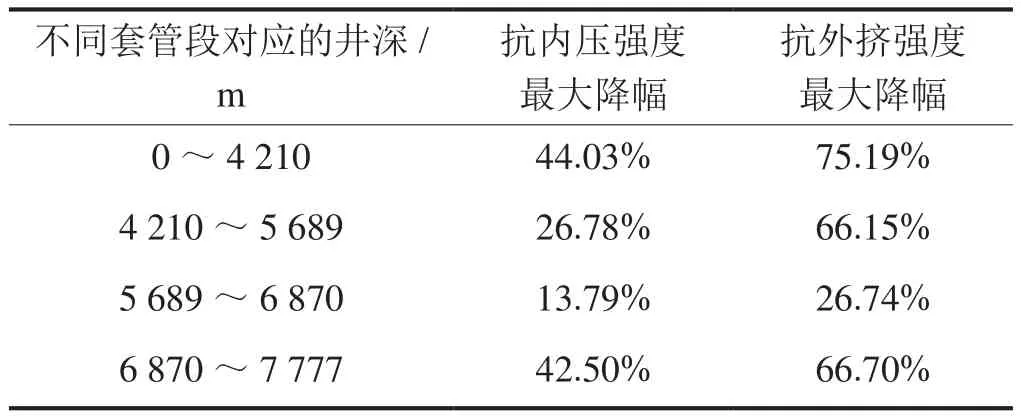
表5 套管磨损后强度降幅表

计算结果表明，磨损对套管强度的影响不可忽略，抗外挤强度还需考虑套管轴向力的影响。如果在施工设计中未充分考虑套管磨损和轴向力的影响，将会高估套管的安全性，导致较高的井筒完整性失效风险。

5 结论

1）套管磨损形状并不仅仅是单月牙，还会出现多月牙重叠、交叉和分离的复合磨损形状。

2）磨损套管的内压失效是一种强度失效，当主磨损区套管壁中部的等效应力达到材料的屈服强度时，内压失效发生；套管的外挤失效是一种稳定性失效，当套管截面形状的椭圆度达到临界值时，外挤失效发生。

3）磨损深度、套管径厚比和材料的屈服强度是套管抗内压强度的主要影响因素；磨损深度、磨损宽度、分离角、径厚比和屈服强度是套管抗外挤强度的主要影响因素。

4）建立了磨损套管剩余强度的智能预测模型，预测精度在90%以上，并结合理论公式对存在轴向力套管的剩余强度计算进行了修正，采用安全系数的方法来预测套管的失效风险。

5）深井超深井钻井过程中套管磨损问题非常突出，磨损对套管强度的影响不可忽略，抗外挤强度还需考虑套管轴向力的影响。若在施工设计中忽略套管磨损的影响，将会严重高估套管的设计强度，导致较高的井筒完整性失效风险。