碎石桩加固砂土地基数值模拟

徐文栋，李学丰，杨文伟

（1.宁夏大学 土木与水利工程学院，宁夏 银川 750021；2.宁夏大学 固体力学研究所，宁夏 银川 750021；3.宁夏土木工程防震减灾工程技术研究中心，宁夏 银川 750021）

0 引 言

风积砂广泛分布于腾格里沙漠地表，是该地区大多数工程建设中地基处理设计与施工都会遇到的特殊土体地基。风积砂作为一种特殊土体，具有颗粒细、级配不良、低渗透性、无黏性等不良的工程特性，这些不良的工程特性给该地区的公路建设带来极大的困难。然而，随着中国经济的高速发展，尤其是“西部大开发”和“一带一路”政策的逐步落实，高速公路的覆盖面积越来越广，在腾格里沙漠区必然会逐步开展公路建设。《国家公路网规划（2013—2030年）》中乌海至玛沁公路（编号：G1816、下称乌玛公路）自西南向经过腾格里沙漠南缘。

乌玛高速沙漠段位于宁夏三大地震带的交织部位，东北侧为华北地震区的银川地震带，西南侧为青藏高原地震区的卫宁地震带及西海固地震带。其中银川地震带与卫宁地震带对本项目影响较大，项目区域历史上发生Ms＞4.7级的地震，见表1。

表1 乌玛公路沙漠区地震调查Table 1 Seismic survey of Wu-Ma highway desert area

根据《中国地震动峰值加速度区划图》（GB 18306—2015）与《中国地震动反应谱特征周期区划图》（GB 18306—2015）的划分，该区域地震动峰值加速度0.20 g，反应谱特征周期为0.45 s，对应地震烈度8度，设计地震分组为第二组，属强震区。

采用碎石桩对可液化地基土层进行加固形成碎石桩复合地基，能够有效提高其地基承载力，减小沉降变形，并且其高渗透性有利于加快土体中超静孔隙水压力的消散[1]。同时具有取材便利、施工快速简便、造价经济等优点，因此被广泛应用于工程实践中[2]。国内外已有许多学者采用理论和试验的方法对碎石桩复合地基的承载力和变形进行了研究[3-6]。由于桩土之间存在着复杂的相互作用限制了理论解析的应用，因此许多学者也采用数值模拟的方法对碎石桩复合地基展开研究。蒋敏敏等[7]通过数值计算，分析了高速公路碎石桩复合地基在桩体施工、路堤路面分层填筑以及交通荷载作用下变形等问题。李华明[8]结合京沪高铁的建设使用碎石桩桩网加固工法对高速铁路饱和粉土液化地基进行了初步设计，对加固前后的饱和粉土地基动力特性和地基路基整体抗震稳定性进行了深入的研究，结果表明加固后土体动强度和液化强度有大幅提高。王武刚[9]对安徽泗浒高速公路区粉砂土地基采用了格栅碎石桩进行处理，通过一系列试验及运用FLAC 3D进行有限元分析，结果表明采用格栅碎石桩加固可液化粉土路基不仅能够充分利用碎石桩的排水减压作用，而且能够增强碎石桩的整体抗剪能力；碎石桩的排水效应对饱和粉土地基抗震液化作用是十分有效的。ADALIER等[10-11]通过振动离心模型试验研究了地震荷载下碎石桩的加固原理和砂土液化机理。HAN等[12]对碎石桩复合地基的固结进行了理论分析，引入修正固结系数来考虑石柱-土模量比的影响。

本文通过 ABAQUS有限元数值模拟软件建立天然地基与碎石桩加固地基模型，模拟并分析了天然地基与碎石桩复合地基在静力和地震动力荷载作用下的力学响应特征，有助于深入认识碎石桩加固砂土地基特性，可为从事地基加固处理相关研究、工程人员提供参考。

1 天然地基模型及计算

1.1 模型尺寸及计算参数

本文中地基模型为平面模型，在X水平方向模型取10 m，Y深度方向模型取20 m。相应的计算参数见表2。

表2 模型计算参数Table 2 Calculated parameters of the model

在模型计算过程中，所有的计算都要满足以下基本假定：（1）土体为完全饱和土，且土中的流体渗流服从达西定律；（2）假定土体的压缩系数和渗透系数为常数，且各向渗透系数取同一常数；（3）土体颗粒和孔隙水具有不可压缩性。

1.2 天然地基静力计算

静力计算采用流固耦合分析步，分析未加固砂土地基在静力荷载作用下的应力、位移、孔压等响应。利用Mohr-Coulomb弹塑性模型使土体在重力及初始应力（100 kPa）作用下达到初始应力平衡，相应的初始孔压云图见图1，竖向应力云图见图2所示。

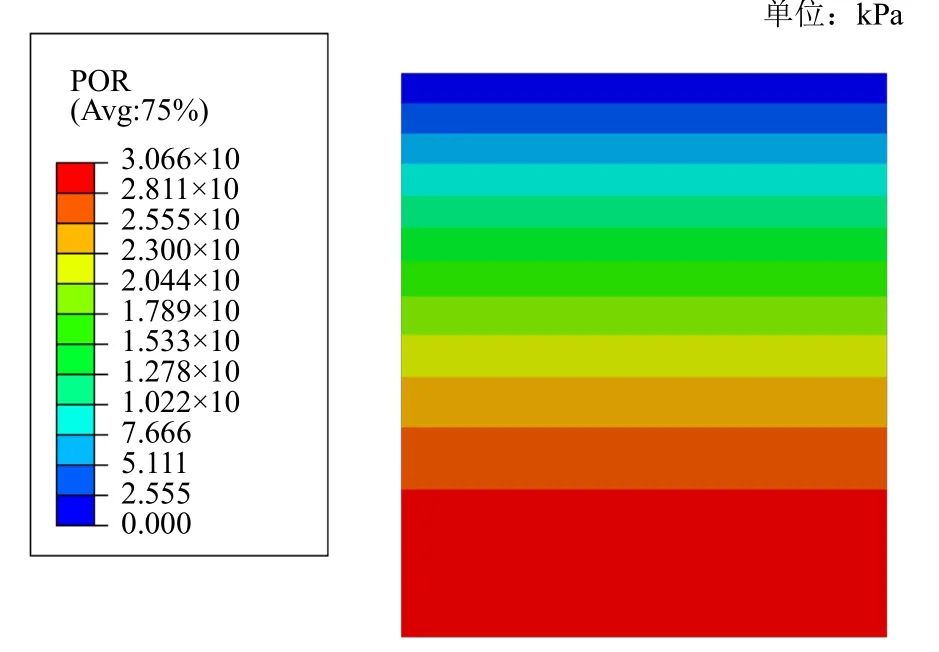
图1 初始孔压云图Fig.1 Initial pore pressure field

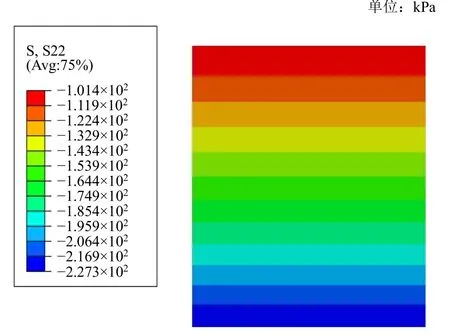
图2 初始竖向应力云图Fig.2 Initial vertical stress field

为了验证计算模型土体所受到的初始竖向应力场是否正确，通常将数值模拟和理论计算的结果进行对比验证分析，并将两者的计算结果进行比较：通过有限元程序 ABAQUS计算得到的应力值为257.9 kPa（227.3 kPa+30.6 kPa）；而按照理论计算公式（σ=γ′h+p0）计算出的土层最底层的竖向应力值为260 kPa，对比可知两者比较接近，说明了通过有限元计算得到的初始竖向应力结果是十分可靠的。

1.3 天然地基动力计算

在动力计算过程中，土体的应力应变关系采用等效线性动力模型，该模型通过迭代的手段来反映土体的非弹性和非线性。由于每个迭代的过程是线性的，这种方法计算效率高，且对于大多数情况，尤其是应变较小（小于2%）、地震加速度在0.3 g的情况下都能提供较精确的结果[13]。等效线性动力模型应力应变关系为：

式中：G是剪切模量；ηG是剪切黏滞系数；τ是剪应力；γ是剪应变。其中：

式中：λ为阻尼比；ω为圆频率。剪切模量比值G/Gmax为：

最大剪切模量Gmax可表示为：

式中：σ3′是围压；pa是大气压；k1、k2、n为材料参数；阻尼比的比值为：

根据等效线性动力模型编制 UMAT用户材料子程序，用于ABAQUS的分析计算中。

运用等效线性动力模型进行动力计算通过以下步骤实现：（1）频率的提取。通过线性摄动分析步提取模型的基频；（2）迭代计算。将上一步中提取的模型基频作为材料的圆频率参数，利用隐式动力分析步，通过迭代计算出各单元的剪切模量比G/Gmax、阻尼比λ和最大剪应变γmax。将每次迭代计算得到的结果作为下次迭代计算的输入参数，整个过程重复几次直到材料性质基本稳定。计算模型底部输入的地震加速度时程曲线如图3所示，其最大峰值为0.1 g。

图3 输入地震波加速度时程曲线Fig.3 Input seismic wave acceleration time-history curve

通过对模型底部输入地震波得到地基底部和顶部的加速度时程曲线如图4所示。由图4可以看出地基顶部加速度相较于地基底部加速度较大。图5为加速的极值沿高度的分布，由图中可明显观察到加速度沿高度的放大现象。

图4 天然地基不同位置水平向加速度时程曲线Fig.4 Horizontal accelerations versus time at different positions of natural ground

图5 加速度极值沿深度的分布Fig.5 Distribution of acceleration extremes with depth

2 碎石桩加固地基

2.1 模型尺寸及计算参数

计算模型选为轴对称模型：在X水平方向模型取 10 m，Y深度方向模型取 20 m。碎石桩桩长取10 m，桩径取0.5 m。桩体采用弹性模型，弹性模量E=20 GPa，泊松比ν=0.15。在静力计算中，砂土地基选用Mohr-Coulomb和修正剑桥模型模拟，碎石桩桩体采用弹性模型模拟。模型顶面设置为加载过程中孔压为0的边界，模型两侧为有侧限的位移边界，模型底部为固定的位移边界。

碎石桩与砂土之间的相互作用通过定义接触面的力学模型，砂土地基与碎石桩之间的法向接触面采用“Hard”接触设定，即假设为当砂土地基与碎石桩之间出现拉力时两者之间接触面即刻分离。两者之间的切向接触类型设定为Coulomb摩擦，即当接触面上剪应力大于它们之间的最大摩擦力时，土体与桩基础之间产生切向相对滑动，本数值模型选取摩擦系数为0.557（tanφ）。

2.2 碎石桩静力计算

首先对碎石桩进行承载力计算，分别选用Mohr-Coulomb和修正剑桥模型模拟砂土地基，得到碎石桩的荷载位移曲线，如图6所示。

图6 碎石桩荷载位移曲线Fig.6 Load-displacement curves of gravel pile

由图6可以看出修正剑桥模型计算出的碎石桩承载力为286.6 kN，Mohr-Coulomb模型计算出的碎石桩承载力为 356.9 kN。图7和图8为 Mohr-Coulomb和修正剑桥模型计算出加载结束时砂土地基的孔压应力云图（文中云图为模型部分代表性区域云图）。两种不同模型均反映出位于桩端的土体产生较大的孔隙水压力，其中Mohr-Coulomb模型计算出的孔压最大值为59.6 kPa，修正剑桥模型计算出的孔压最大值为12.1 kPa。虽然修正剑桥模型计算出的孔压最大值小于Mohr-Coulomb模型计算出的孔压最大值，但剑桥模型计算出正的孔压影响范围大于Mohr-Coulomb模型计算出正的孔压影响范围。

图7 复合地基孔压场（Mohr-Coulomb模型）Fig.7 Pore pressure field of composite foundation (Mohr-Coulomb model)

图8 复合地基孔压场（修正剑桥模型）Fig.8 Pore pressure field of composite foundation (Modified Cam-Clay model)

2.3 碎石桩复合地基动力计算

通过对碎石桩加固的砂土地基模型施加图3所示的地震波，得到其模型底部和顶部的加速度时程曲线，如图9所示。

图9 复合地基底部和顶部水平向加速度时程曲线Fig.9 Horizontal accelerations versus time at different positions of composite ground

通过将图9与图4对比可以发现碎石桩加固砂土地基的峰值加速度小于天然地基的峰值加速度。值得注意的是，在地震波施加后期（峰值加速度之后）碎石桩加固砂土地基的加速度大于天然地基。主要原因是在加载初期由于碎石桩的作用使土体抗剪切能力增强，而在加载后期土体已经出现较大的变形，此时碎石桩对提高土体抗剪切能力并不起作用。

根据数值计算的结果绘制出路基中最大剪应力沿深度的分布情况，如图10所示。SEED等[14]研究发现当地基中动剪应力大于某一值时，地基中土体将发生液化。由图10可知碎石桩加固的砂土地基可在一定程度上降低桩端土体的动剪应力，因此能够提高土体的抗液化强度。

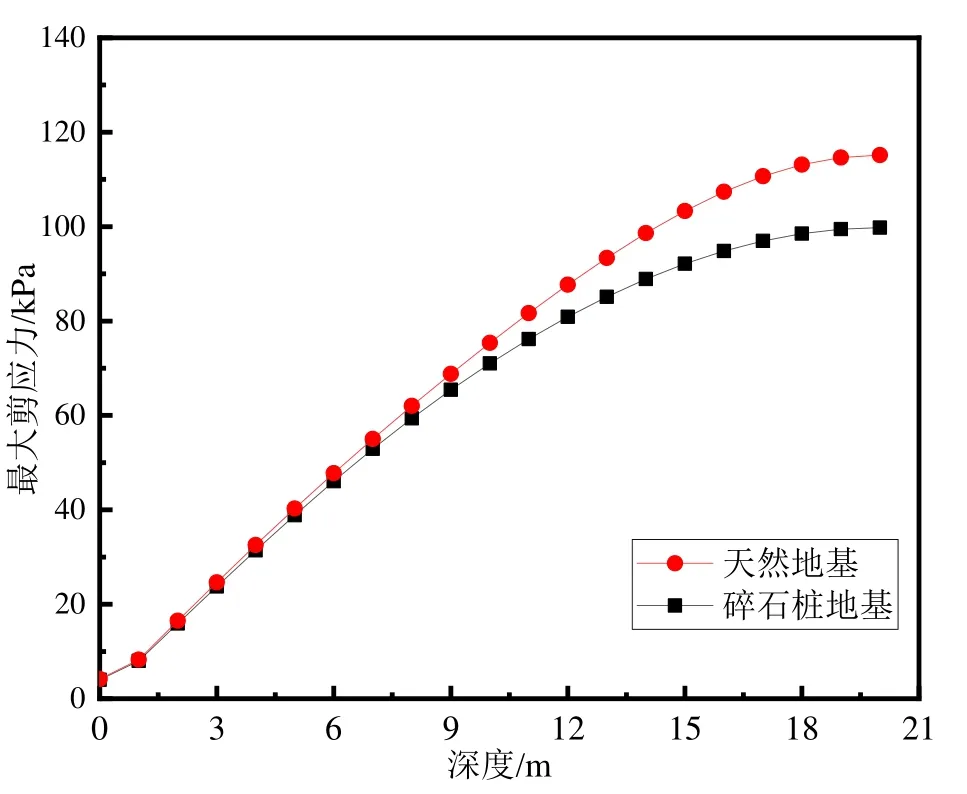
图10 最大剪应力沿地基深度分布Fig.10 Distribution of maximum shear stresses along foundation depth

3 结 论

通过数值计算，分析了天然地基与碎石桩复合地基在静力与地震动力荷载条件下的响应，得到如下结论：

（1）在地震荷载的作用下等效线性动力模型能够较好的模拟地基土体的响应，其地基顶部的水平向加速度相较于地基底部的水平向加速度较大。在天然地基内，随着深度的降低其水平加速度极值逐渐增加。

（2）砂土模型采用修正剑桥模型计算出的碎石桩承载力为286.6 kN，Mohr-Coulomb模型计算出的碎石桩承载力为356.9 kN。在地震荷载的作用下，碎石桩加固砂土地基的峰值加速度小于天然地基的峰值加速度。在整个地基内，碎石桩加固的砂土地基可在一定程度上降低桩端土体的动剪应力，土体的抗液化强度显著提高。