多尺度离散裂缝性致密砂岩气藏数值试井新方法——以塔里木盆地克拉苏气田为例

孙贺东 欧阳伟平 朱松柏 万义钊 唐永亮 曹 雯

1.中国石油勘探开发研究院 2.中国石油川庆钻探工程有限公司长庆井下技术作业公司 3.中国石油塔里木油田公司 4.青岛海洋地质研究所

0 引言

塔里木盆地深层超高压气藏资源丰富，尤其以库车山前盐下白垩系砂岩气藏最为富集[1-5]。气藏特征国内外罕见，具有埋深大、地表地下构造复杂、基质储层致密、断裂系统发育且非均质性强、气藏温度及压力高等特殊地质条件，具有井间产能差异大、压力响应异常迅速、水侵高速不均匀等生产特征，可谓集多种复杂情况于一身。储层动静态描述难度大，气藏高效开发过程中遇到诸多世界级难题。储层天然裂缝及断层发育，储层包含基质、裂缝及断层（大裂缝）三种孔隙介质，非均质性强，渗流机理复杂[6-7]，现有连续介质渗流理论难以精确描述其渗流规律、开发机理以及储层动态特征[8-9]。天然裂缝发育具有较强的随机性，给描述储层天然裂缝分布带来了很大挑战[10]。通过地震资料解释可获得大裂缝信息，但无法确定中小裂缝和未测量区域的裂缝，因此根据已知信息建立确定裂缝模型的方法很难用于描述微裂缝极其发育的储层。20世纪80年代开始，基于统计理论建立随机裂缝网络模型的方法在岩石工程研究中得到了广泛应用[11-20]。虽然无法对储层内所有的裂缝都进行测量，但可根据区域地质统计的裂缝几何参数概率分布函数来模拟服从这些分布规律的裂缝网络。利用Monte-Carlo法随机生成裂缝网络，不仅满足已知区域的裂缝统计学特征，而且描述了未知区域裂缝发育的随机性，与研究区域内的实际裂缝具有统计学上的相似性[21]。

裂缝性储层的试井模型可以分为连续介质模型[22-25]和离散裂缝模型[26-32]两大类。目前以连续介质模型为主，该类模型基于连续介质假设，即假定储层中任何一个位置同时存在裂缝和基质两种介质。实际储层天然裂缝通常表现为离散、不规则特征，裂缝在长度、开度以及间距等方面存在差异，尤其在裂缝分散、间距较大的情况下，采用双重或者三重孔隙连续介质来描述孔—缝—断（大裂缝）的裂缝性储层，与实际情况存在较大偏差，将造成试井曲线无法拟合、解释参数误差较大的情况。对储层认识不正确，将导致开发决策失误。离散裂缝模型则通过对裂缝（断层）进行显式处理来准确描述任意裂缝的形态、方位及导流能力，因此该模型在处理裂缝性砂岩储层上具有明显的优势。然而，目前离散裂缝模型的裂缝为确定性裂缝，不适用高度随机发育的裂缝性储层。

为此，通过分批次分区域的天然裂缝网络随机生成方法构建多尺度离散裂缝网络，建立一种考虑断层（大裂缝）、裂缝和基质3种孔隙介质的直井不稳定渗流数学模型。对裂缝及断层降维处理，采用非结构化网格对离散裂缝网络进行完全匹配，利用三角单元和线单元混合的有限元方法对模型进行求解，旨在满足试井动态模拟的早期高精度要求，进而实现非连续多尺度渗流精确表征。将离散裂缝模型结果与传统双重孔隙介质模型的结果进行对比，探讨双重孔隙介质模型的适用条件，分析讨论不同随机缝网分布模式的试井典型曲线特征，并讨论缝网随机生成对试井曲线的影响，最后用现场实例应用验证模型的可靠性及实用性。

1 天然裂缝网络随机生成方法

针对实际地层存在不同尺度的裂缝网络且不同区域裂缝发育存在较大差异的特点，通过分批次分区域多次随机生成裂缝再组合的方式构建多尺度随机裂缝网络。随机生成的裂缝网络中每组裂缝的每个几何参数都可以采用一种概率分布函数表示，这些分布会随裂缝组数和几何参数的不同而变化，主要有均匀分布、标准正态分布、对数正态分布、指数分布和Fisher分布等。根据实际情况选择合适的概率分布函数，采用Monte-Carlo逆变换方法模拟实现所选取概率分布的随机抽样，生成满足上述概率分布的随机数列[33-34]。随机数的数量越大，随机数概率分布越接近于所选择的概率分布函数。

1.1 裂缝中心位置随机生成

试井测试储层范围内裂缝中心位置基本满足均匀分布特征，因此为了研究方便，按照均匀分布的方式随机生成，均匀分布随机变量的概率密度函数为：

式中a、b分别表示随机变量选取范围的最大值和最小值。

假设ξ为[0,1]区间均匀分布的随机数列，则：

式中ηc表示[a,b]区间均匀分布的随机数列，ξ由计算机提供的随机数生成函数生成。

由式（2）得到：

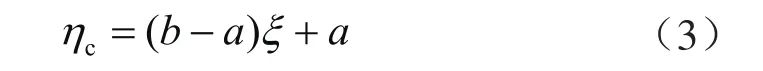
1.2 裂缝长度随机生成

天然裂缝长度虽然也是随机分布，但裂缝长度越大，概率密度越小，因此假定天然裂缝长度满足指数分布。采用指数分布的随机数生成方法生成裂缝长度数据。指数分布随机变量的概率密度函数为：

式中μ表示随机变量的最小值，λ表示大于0的系数。通过积分求逆法得到：

式中ηl表示大于μ服从指数分布的随机数列，其数学期望为μ+1/λ。

根据公式（6）的物理意义，可以得到生成裂缝长度随机数的公式：

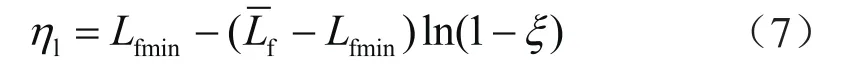
式中Lfmin表示最小裂缝长度，m；表示平均裂缝长度，m；ξ表示[0,1]区间均匀分布的随机数。

1.3 裂缝方位随机生成

由于地应力的影响，天然裂缝存在一定的方向，为此假定天然裂缝方位满足正态分布。采用正态分布的随机数生成方法生成裂缝方位数据。正态分布随机变量的概率密度函数为：

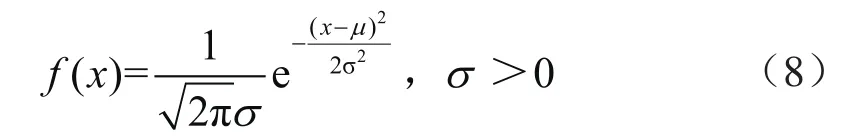
式中σ表示标准差，μ表示数学期望。

标准正态分布的累计分布函数为：

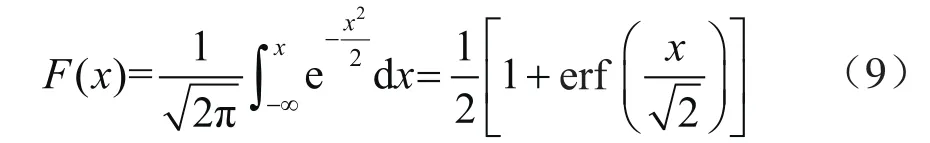
式中erf表示误差函数。

由此得到标准正态分布随机数：

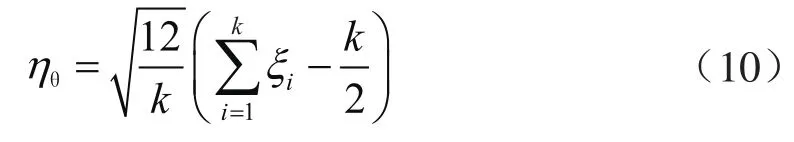
式中k表示随机变量的个数。

裂缝方位角随机数生成公式为：

1.4 裂缝随机生成效果

利用上述随机裂缝生成方法，可以生成各种裂缝分布形态，如图1所示。相同的随机裂缝生成参数，并不一定生成相同的裂缝分布，但两者具有统计上的相似性。针对不同区块裂缝发育差异性较大的问题，可以通过裂缝数量（裂缝密度）和平均裂缝长度来控制发育的程度，通过裂缝方位角控制裂缝发育的方向，此外还可以通过叠加两种类型裂缝来区分断层和小裂缝，并将两者导流能力差异化设置，从而实现多尺度裂缝的描述。

图1 裂缝随机生成效果图

2 离散裂缝网络试井模型

2.1 物理模型及假设条件

考虑裂缝性致密砂岩气藏储层中有一口直井，井筒周边存在断层（大裂缝）、天然裂缝和人工裂缝，如图2所示。模型假设条件如下：①原始储层存在3种孔隙介质，分别为基质、裂缝和断层（大裂缝），3种介质的渗透率差异至少在一个数量级以上；②忽略气体滑脱效应[35]，气体流动为单相渗流，且满足达西定律；③流体在裂缝和断层中的流动为一维流动，在基质中的流动为二维流动，裂缝和断层均为有限导流裂缝，但导流能力各不相同；④天然裂缝与断层（大裂缝）按照概率分布函数随机生成，人工裂缝为双翼对称缝。⑤气体压缩系数、黏度、偏差系数等高压物性参数是压力的函数，考虑井筒储存效应和表皮效应。

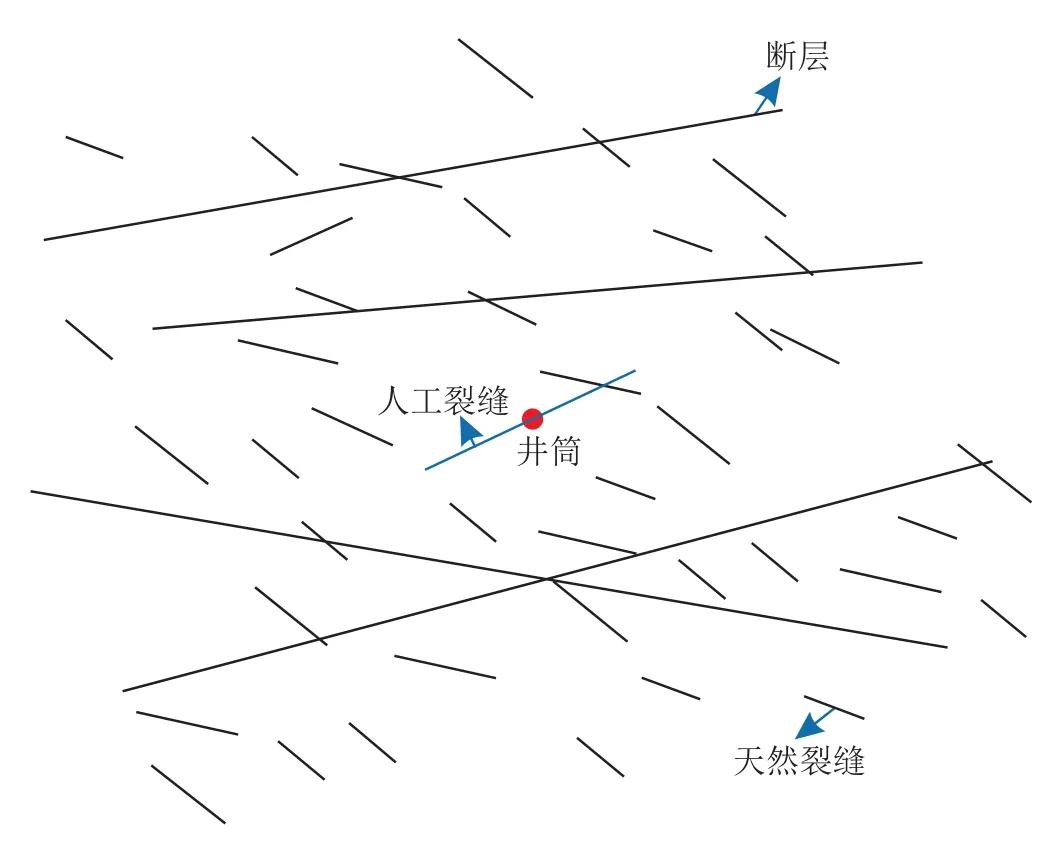
图2 物理模型示意图

2.2 数学模型

2.3 模型求解

利用非结构化网格离散技术对包含随机裂缝的计算区域进行Delaunay三角网格剖分，剖分后的网格与裂缝网络完全匹配。对裂缝和断层中流体流动进行降维处理，使裂缝、断层成为一维线单元，基质为二维三角单元。基于混合单元有限元方法对模型进行求解，将整个计算区域划分为流体发生二维流动的基质区域、流体发生一维流动的天然裂缝区域、断层区域和人工裂缝区域4个部分。在求解数学模型时，利用Galerkin加权余量法推导出基质、裂缝和断层单元的有限元计算格式，根据有限元计算格式建立单元刚度矩阵，再由单元刚度矩阵组成系统刚度矩阵，实现基质、裂缝和断层耦合流动问题的求解，具体求解方法可以参考本文文献[36]。

3 离散裂缝模型与双重孔隙介质模型对比

传统双重孔隙连续介质模型是一种理想的视均质模型，为了探讨其适用条件，对比传统连续介质模型与离散裂缝模型的结果。采用Saphir软件的双重孔隙介质非稳态窜流模型计算连续介质模型结果，为了便于对比，简化本文离散裂缝模型，暂且仅考虑天然裂缝，忽略断层（大裂缝和小断距断层）和人工裂缝，并假设天然裂缝连续且均匀正交分布。由于正交缝网间距对两种模型的对比结果具有较大影响，为此分别讨论裂缝间距为5 m×5 m和0.5 m×0.5 m的正交缝网结果。

3.1 5 m×5 m正交缝网

假定天然裂缝正交，横纵方向的间距均为5 m，渗透率均为200 mD，宽度均为0.01 m，基质渗透率为0.01 mD，井筒半径为0.1 m，根据等效换算，双重孔隙介质模型中储容比为0.004，窜流系数为0.000 32，等效裂缝渗透率为0.4 mD。假定储层孔隙度为10 %，初始地层压力为50 MPa，温度为120 ℃，圆形外边界半径为100 m。分别采用离散裂缝模型与双重孔隙非稳态模型计算以产量10 000 m3/d生产1 000 h的压降，由此得到的试井曲线如图3所示。

图3 5 m×5 m离散裂缝模型与双重孔隙介质模型试井曲线对比图

从图3中试井曲线对比可知，即使假定裂缝连续且正交，双重孔隙介质模型与离散裂缝模型仍然存在一定的差异，尤其是早期井筒储存效应、表皮效应阶段，后期窜流阶段、径向流阶段及拟稳定流阶段的导数曲线基本一致，两者主要差异可通过表皮系数来处理。本算例中裂缝穿过井筒时，离散裂缝模型要比双重孔隙介质模型的流动阻力更小，表现为更小的拟表皮；当裂缝不穿过井筒时，离散裂缝模型计算的流动阻力要大于双重孔隙介质模型。图4为离散裂缝模型裂缝正好穿过井筒时的压力场分布，由图可知，压力率先沿着天然缝网扩散，然后逐渐扩展到基质。裂缝与基质压力传导的快慢由两者渗透率差异决定，即双重孔隙介质中所定义的窜流系数。裂缝渗透率越大，基质渗透率越小，压力场在裂缝中的扩散速度更快，在基质中的扩散速度越慢。

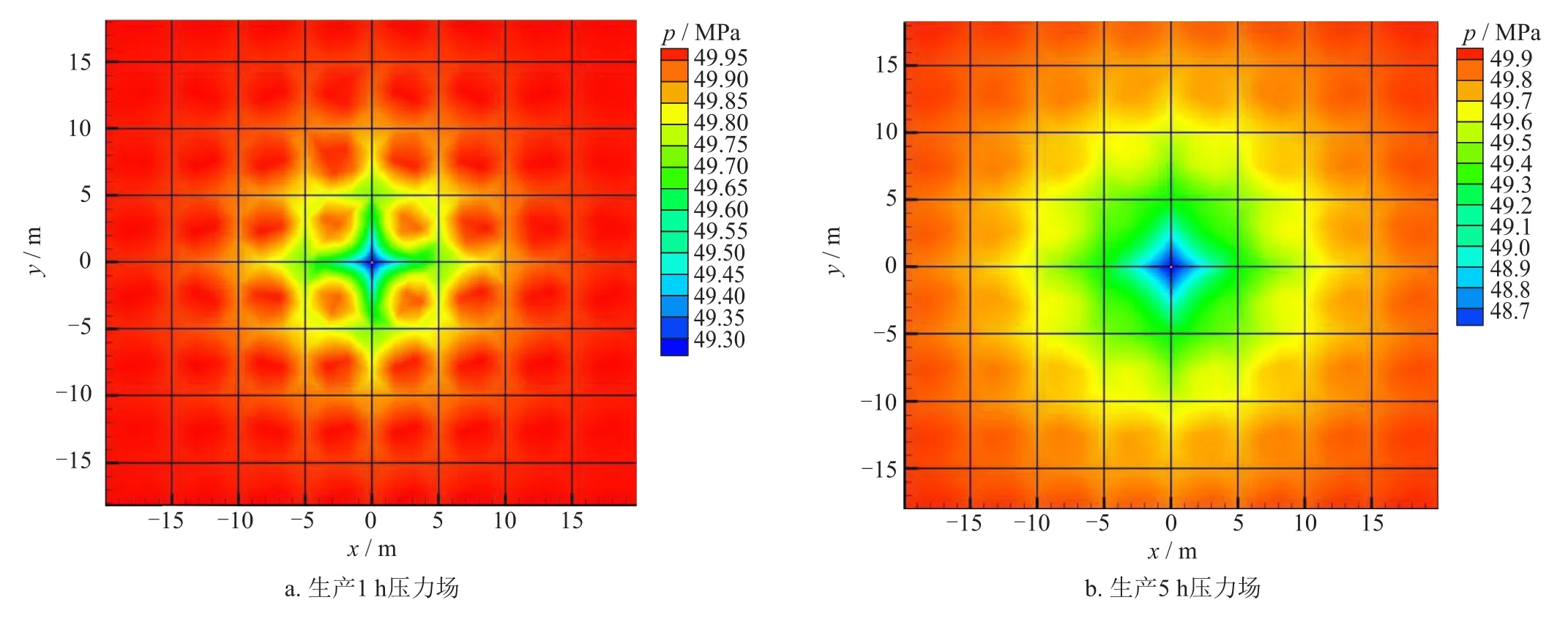
图4 5 m×5 m正交缝网离散裂缝模型压力场分布图

3.2 0.5 m×0.5 m正交缝网

假定正交天然裂缝横纵方向的间距均为0.5 m，渗透率均为1 000 mD，宽度均为0.01 m，基质渗透率为0.1 mD，井筒半径为0.1 m，根据等效换算，双重孔隙介质模型中储容比为0.04，窜流系数为0.006 4，等效裂缝渗透率为20 mD。假定储层孔隙度为10%，初始地层压力为50 MPa，温度为120 ℃，圆形外边界半径为30 m。分别采用离散裂缝模型与双重孔隙介质模型计算以产量10 000 m3/d生产100 h的压降，得到的试井曲线如图5所示。

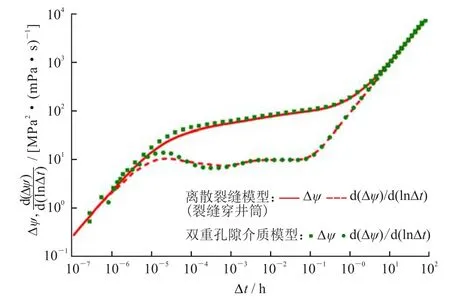
图5 0.5 m×0.5 m离散裂缝模型与双重孔隙介质模型曲线对比图

从图5中试井曲线对比可知，相比于5 m×5 m正交缝网，0.5 m×0.5 m的离散裂缝模型与双重孔隙介质模型计算结果的差异更小，除了井筒表皮阶段存在较小差异外，其余阶段两者基本一致。相比于5 m×5 m缝网，0.5 m×0.5 m缝网更快达到系统径向流。两种模型对比结果可以说明双重孔隙介质模型仅仅是离散裂缝模型中裂缝均匀分布且间距无限小的一种特例，因此双重孔隙介质模型严格上只适用于裂缝分布均匀且间距较小的储层。

4 不同随机缝网分布模式的试井曲线特征

克拉苏气田克深2气藏井下测试数据表明，试井双对数图表现为离散裂缝性储层特征，压力导数后期上翘，斜率介于0.5～1之间[37]，即使测试时间超过1 000 h，也未出现径向流，说明基质渗透率很低，可划分为如下三种模式。

4.1 I类模式（方向性断层发育+裂缝部分发育）

该模式发育方向性断层（大裂缝，小断距断层），并伴有小裂缝，但小裂缝发育不充分，储层渗流特征表现为具有明显的方向性。为计算该模式的试井曲线特征，假定纵向断层发育，数量200条，导流能力为104mD·m，平均长度200 m，横向发育少量裂缝，数量100条，导流系数分别为100 mD·m、500 mD·m和5 000 mD·m，平均长度100 m，基质渗透率0.1 mD。根据所建立的渗流模型计算得到该模式的典型试井曲线如图6所示，压力场如图7所示。从计算结果可知，该地质模式下的试井典型曲线未见到水平井径向流线，经过井筒储存效应和表皮效应阶段后，表现为裂缝线性流动特征，但是由于裂缝发育各向异性使得流动后期压力导数曲线斜率并非0.5，而是介于0.5～1之间，斜率值主要由两个方向（裂缝与断层）导流能力差异大小决定，差异越小，斜率越大。压降曲线在封闭边界的影响下最终均变为斜率值为1的直线，压恢曲线由于裂缝发育，压力趋于稳定的时间较早，压力导数曲线“下掉”。图7中显示的压力场也能充分反映出地层线性流动特征，以方向性断层走向决定地层线性流动方向，但由于储层还发育另一方向的小裂缝，因此该线性流动并非严格意义上的单方向线性流动，也就造成了试井双对数导数线斜率值并非严格为0.5。

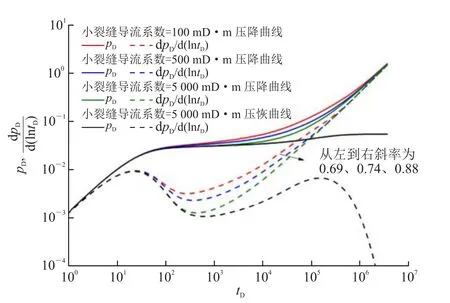
图6 I类缝网分布模式的试井典型曲线图

图7 I类缝网分布模式的压力场分布图

由于天然裂缝均由计算机随机生成，因此有必要讨论相同参数下随机生成对试井典型曲线的影响。图8为按照相同参数随机生成3次天然裂缝下的试井曲线对比图，从对比结果可知，3次随机裂缝下的试井典型曲线并不完全一致，虽然天然裂缝是按照一定的概率统计生成得到，但是空间分布还是存在一定的差异，尤其是井筒周围裂缝分布的差异对试井典型曲线的影响较大，但是3次随机裂缝表现出具有相似的试井曲线形态，且后期线性流斜率基本一致。实际解释过程中，随机裂缝分布带来的影响也可以通过表皮效应来近似处理，具体增加还是减小表皮系数需根据导数曲线“驼峰”的高低来判断。

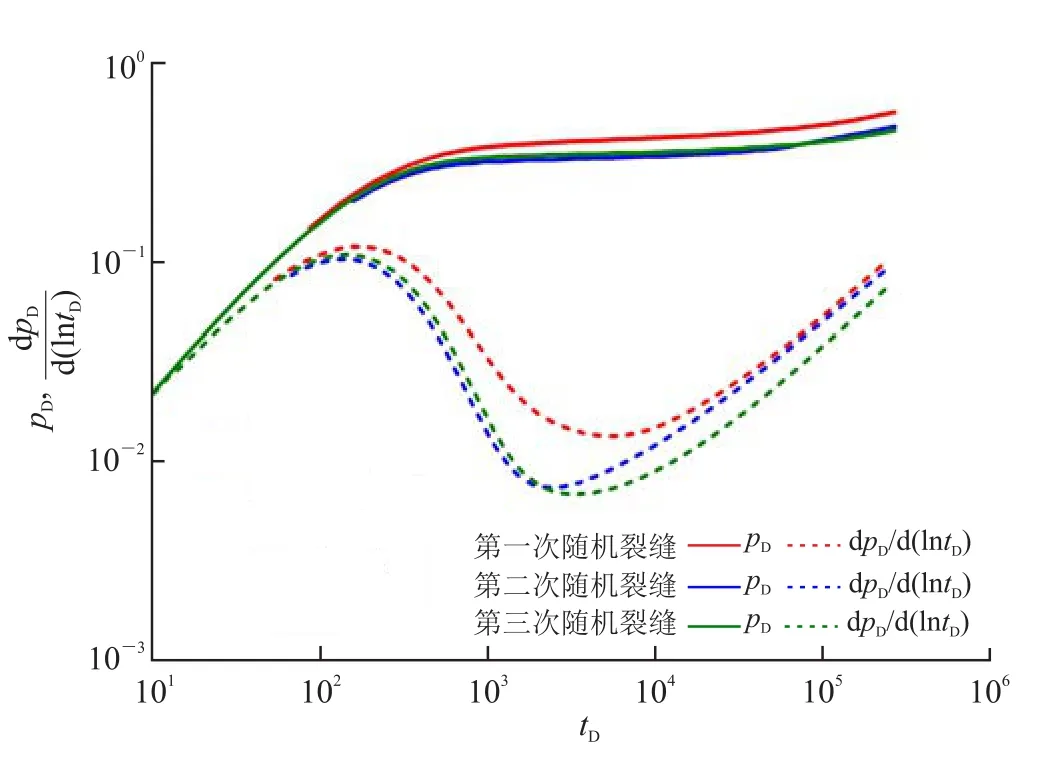
图8 裂缝随机生成对试井典型曲线的影响图

4.2 Ⅱ类模式（裂缝发育+断层贯穿）

孔—缝—断的组合模式为裂缝多方向发育+断层贯穿+基质。为计算该组合模式下的试井典型曲线，假定天然裂缝400条，平均长度150 m，天然裂缝导流能力分别设置为200 mD·m、1 000 mD·m和5 000 mD·m，基质渗透率0.1 mD，断层（大裂缝，小断层）贯穿，断层导流能力为104mD·m。计算得到该模式的典型试井曲线如图9所示，压力场如图10所示。从计算结果可知，该模式多方向天然裂缝相互沟通，压力向多方向扩散，并很快达到裂缝系统的流动拟稳态，此后基质往裂缝中流动，试井压力导数曲线呈现斜率值为1的直线。裂缝导流能力越大，井筒储存效应、表皮效应阶段过后的压力导数曲线“下掉”得越明显，压力曲线值越小，表明流动阻力越小。由于裂缝发育充分，并有断层贯穿，流动阻力较小，压力扩展速度很快，压力扩散在较短时间内就波及到了整个区域，且整个区域的压差较小，如图10所示。此外，从压力场分析可知压力扩散形态与裂缝分布及裂缝沟通情况息息相关。

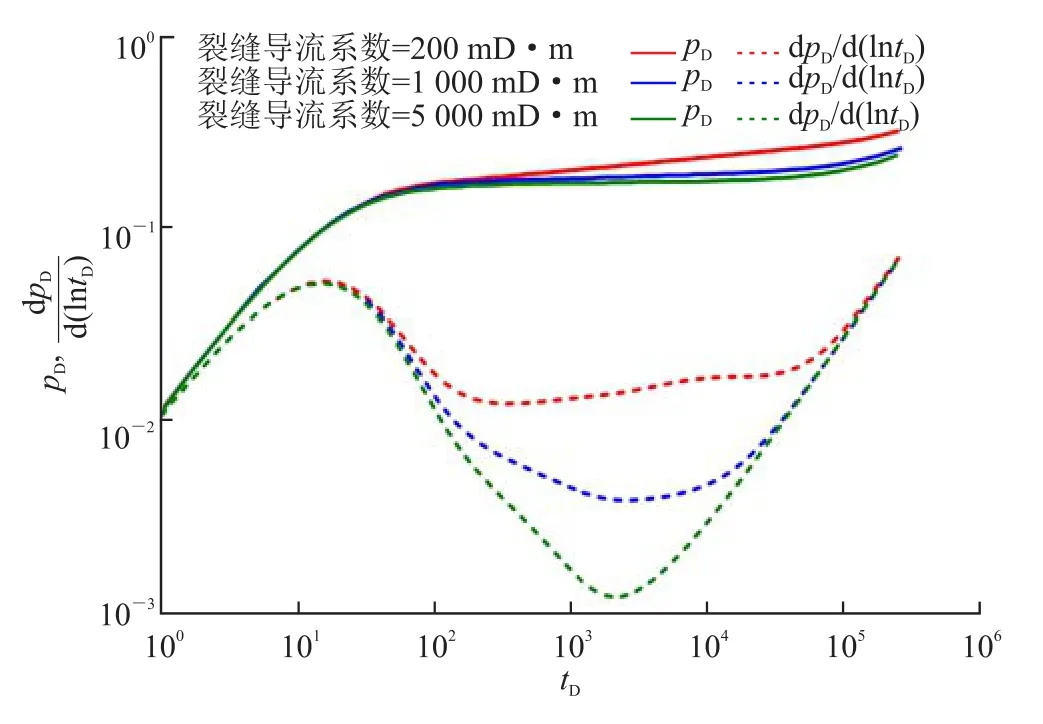
图9 Ⅱ类缝网分布模式的试井典型曲线图

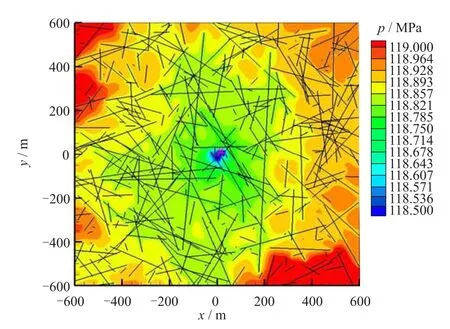
图10 Ⅱ类缝网分布模式的压力场分布图

4.3 Ⅲ类模式（短裂缝高度发育，无断层）

该模式多方向发育高密度低导流能力的短缝，无断层贯穿。为计算该模式的试井曲线，假定裂缝多方向发育，数量2 000条，平均长度20 m，导流系数500 mD·m，基质渗透率0.4 mD。计算得到该模式的典型试井曲线如图11所示，压力场如图12所示。由于裂缝长度和导流能力均较小，导致试井曲线压降幅度较大，生产压差较大，小裂缝分布较均匀，因此试井压力导数曲线能够呈现系统径向流，由于天然裂缝的影响，径向流压力导数值小于0.5。压力场也呈现出拟径向流方式的压力扩散特征，在外边界作用下斜率值为1的直线。该缝网分布模式下的试井曲线特征与双重孔隙介质非稳态窜流模型的试井曲线特征具有一定的相似性。

5 实例应用

塔里木盆地克拉苏气田是我国第一个成功开发的深度超过8 000 m的气田，目的层为下白垩统巴什基奇克组，属于扇三角洲—辫状河三角洲前缘相沉积，砂体厚度大，横向叠置连片，隔/夹层不发育。储层基质物性较差，岩心孔隙度介于2%～8%，平均值为4.1%；基质渗透率介于0.001～0.100 mD，平均值为0.05 mD。受强构造挤压变形影响，断裂发育且储层非均质性强。气藏埋深普遍为6 000～8 000 m，原始地层压力90～150 MPa，地层温度125～190 ℃，属超深超高压高温气藏[38-39]。

克拉苏气田克深2气藏为斜向挤压变形区，发育一系列基底卷入式逆冲断层，不同级别裂缝发育，投产前储层普遍进行体积改造。其中一口气井于2016年4月至5月进行了压力恢复测试，该井关井前日产量为57.1 ×104m3。该井储层厚度161 m，基质孔隙度为6.45%，储层温度为160 ℃，气体相对密度0.57。压恢试井曲线形态如图13所示，测试时间超过200 h，但未出现径向流，用常规试井模型无法进行试井解释，利用本文所建立的随机离散裂缝模型对该井进行压恢试井解释，解释结果如表1所示。

图13 克拉苏气田某井试井双对数曲线拟合图

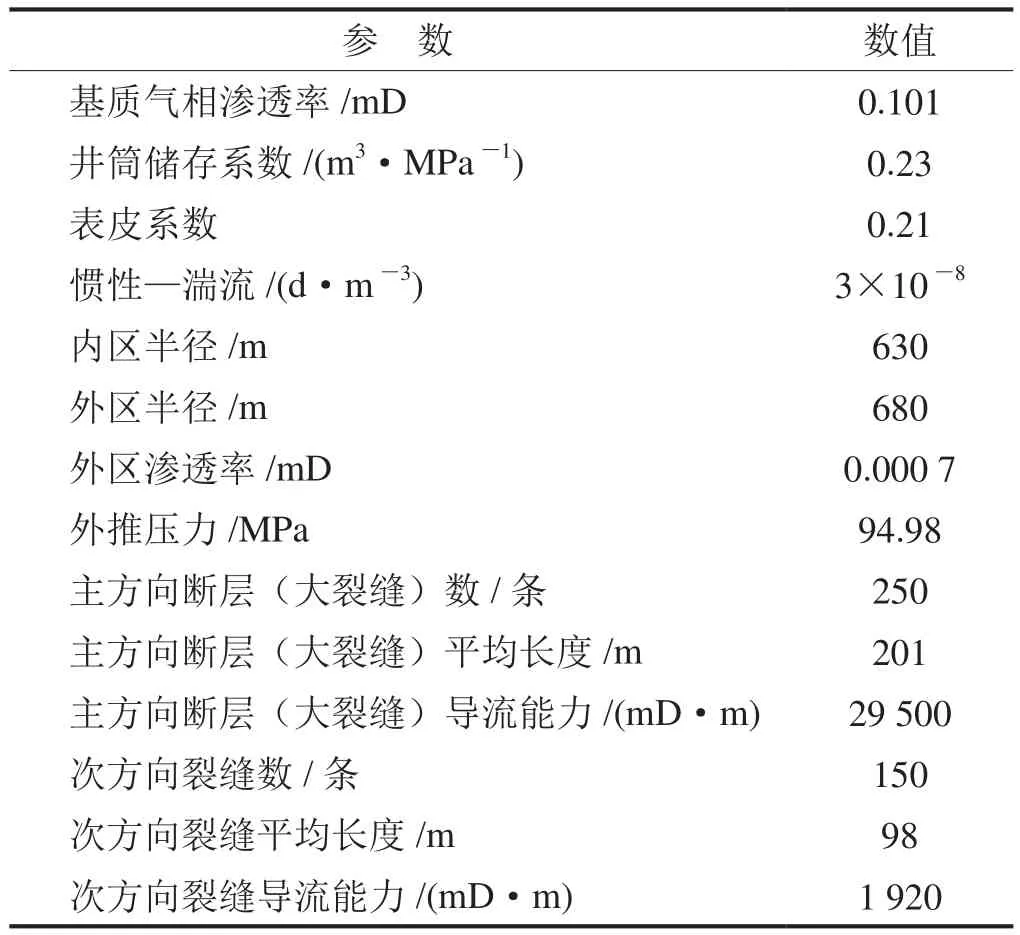
表1 克拉苏气田某井压恢试井解释结果数据表

实测试井压力导数曲线无径向流水平线特征，井筒储存效应、表皮效应阶段过后，压力导数曲线“下掉”程度较大，后期曲线斜率值为0.68，曲线综合表现符合本文Ⅰ类缝网分布模式的试井曲线特征，这与该区块挤压型高陡式断背斜构造特征符合[40]。因此采用方向性断层发育+裂缝部分发育组合的方式进行随机裂缝建模，根据实际曲线拟合情况，将I类随机缝网分布模式与分区复合模型进行结合，内区为随机方向性断层和裂缝部分发育组合，外区为致密区。从双对数曲线拟合图可知，本文模型计算的典型曲线与实测曲线具有较好的一致性，而采用常规双重孔隙或三重孔隙连续介质模型无法对该测试曲线进行拟合，主要原因在于该井地层裂缝随机发育具有较大离散性，非均质性较强，连续介质模型无法进行等效处理。本文方法不仅可以获得常规储层参数，还可以获得天然裂缝及断层参数，为了解储层天然裂缝发育情况提供了有效手段，达到了以动补静的效果，进而为合理开发技术政策的制定及后期提高采收率奠定了基础。

6 结论

1）离散裂缝模型与传统双重孔隙介质模型结果对比表明，裂缝间距较大情况下，离散裂缝模型与双重孔隙介质模型结果存在较大差异，但在小间距正交缝网条件下，两者结果基本一致，说明双重孔隙介质模型是离散裂缝模型中裂缝均匀分布且间距无限小的一种特例。

2）相同概率统计参数下生成的裂缝空间分布存在一定差异，尤其是井筒周围裂缝分布的差异对试井典型曲线的影响较大，因此相同参数下裂缝网络随机生成的试井典型曲线并不完全一致，但是随机裂缝表现出具有相似的试井曲线形态。

3）分别讨论了3种缝网分布模式下的试井曲线特征，研究结果表明：Ⅰ类缝网分布模式后期压力导数曲线斜率值介于1/2～1，这是识别这种模式的重要特征。Ⅱ类和Ⅲ类缝网分布模式下，试井压力导数曲线后期呈现斜率为1的直线，Ⅲ类模式的试井曲线存在系统拟径向流特征，且生产压差大于Ⅰ类和Ⅲ类。从压力场分布可知，断层贯穿的地层压力扩散非常快，且整个区域的压差非常小。

4）应用所建立的随机离散裂缝试井解释模型成功解释了常规双重孔隙三重孔隙连续介质无法解释的试井测试曲线，曲线拟合效果理想，解释得到的参数合理。

5）本文模型突破了双重连续介质渗流理论的局限，揭示了不同尺度介质间逐级动用、协同供气的开发机理，解释了井间产能差异大、井间压力响应异常迅速的开发特征，进而为合理开发技术政策的制定及后期提高采收率奠定了基础。