中子能谱测量中的解谱技术研究进展

黄迁明，刘 斌，陆 婷，王 波，唐松乾，吕焕文，应栋川，翟梓安

(中国核动力研究设计院核反应堆系统设计技术重点实验室，成都 610213)

中子能谱测量是中子探测学的重要组成部分[1-4]，主要用于获取准确的中子能谱信息，通过相应解谱算法的研究，可在一定程度上提高实验测量的精度，且解谱算法性能的提高有助于在有限测量条件下降低探测系统硬件的要求，在各类核装置的设计和运行、辐射防护计量学和屏蔽验证、核军备控制以及反恐等应用中发挥着关键作用。近年来，在核不扩散和核军备反恐安检的大应用背景下，基于中子能谱的核素识别技术对于核材料准确、高效的识别具有很强的优势[5-9]，国内外在中子能谱的解谱方法上进行了广泛研究。中子能谱测量难度较大，主要面临中子能谱差异大、中子能量跨度区间大、伽马本底干扰、中子场的统计涨落和测量系统噪声等问题[10-12]。目前中子能谱测量的手段主要有：飞行时间方法[13]、有机闪烁体测量方法[14-19]、多球谱仪方法[20-23]以及多箔活化方法[24-26]等。除飞行时间法外，其余三种测量方法的中子能谱均不能直接获取，而是需要结合探测系统的响应函数从测量值中进行解谱获得，即通过探测器探测到一个输入能谱，根据探测器对不同中子的响应特性，反推出测量点的真实能谱。现阶段能谱测量的难点主要由探测器测量数据统计误差、测量系统的噪声干扰、解谱函数不具有唯一解以及先验谱的可靠性造成，通过优化探测系统和解谱算法能一定程度上提高中子能谱测量精度。

1 国内外中子能谱解谱方法研究现状

1.1 解谱模型

在经典的解谱模型中，对于有机闪烁体、多球谱仪以及多箔活化测量系统，探测器测量结果均可用式(1)所示的第一类Fredholm积分方程表征[27-28]：

(1)

式中，Mi为探测器计数，对于有机闪烁体测量系统，其为第i道闪烁光子脉冲高度；对于多球谱仪测量系统，其为第i个慢化球对应的热中子探测器计数；对于多箔活化测量系统，其为第i个活化箔辐照结束后的放射性活度；εi为测量结果的不确定度，其通常与探测器计数的统计特性、中子场统计涨落以及测量系统电子学噪声等因素相关；Ri为第i个探测器的中子能量响应函数，对于有机闪烁体测量系统，其为第i道多道不同中子入射产生的闪烁光子脉冲高度分布；对于多球谱仪测量系统，其为第i个慢化球对应的中子能量响应函数；而对于多箔活化测量系统，其为第i个活化箔对应的活化反应的多群截面；φ(E)为所要求解的中子能谱。

而求解式(1)面临诸多困难，包括：(1)方程组不具有唯一解；(2)误差引起解的剧烈震荡，从而造成求解的失败；(3)探测器计数的统计特性、测量系统的噪声及中子辐射场本底造成求解困难；(4)解的非负值约束、系统响应不确定性的传递等问题。

因此，该类问题在测量领域被称为“逆问题”，利用测量系统的响应函数对真实能谱进行倒推成为解谱的新思路。

1.2 响应函数获取

响应函数的获取是中子能谱解谱的前提，针对不同的中子能谱测量方式可以制定对应的响应函数测量方法，一般有实验测量方法和理论计算结合实验标定方法。

1.2.1实验测量

在有机闪烁体测量实验中，通常的手段主要采用单色性较好的加速器中子源结合飞行时间法对中子能量进行甄别，比如Lawrence等人[29]采用加速器中子源结合飞行时间窗对EJ-309和EJ-299-33有机闪烁体的响应函数进行测量得到图1的响应函数。而在多球谱实验中，主要的实现方法是采用加速器中子源结合慢化材料以实现不同能量中子的响应函数标定，同样采用飞行时间方法对中子能量进行甄别，图2为Pioch等人[30]采用加速器中子源对多球谱仪系统进行能量标定的方案。

图1 EJ-309和EJ-299-33有机闪烁体相关能点的系统响应函数

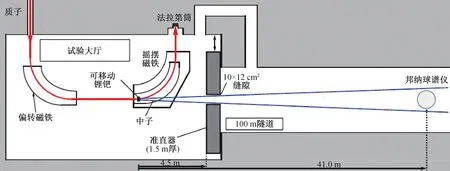
图2 采用加速器中子源标定多球谱仪能量响应方案

1.2.2理论计算结合实验标定

在有机闪烁体测量实验中，Dickens等人[31-32]开发了基于蒙特卡罗算法的SCINFUL、NRESP7等程序进行闪烁体响应函数计算，但它们仅适用于圆柱几何，且无法描述复杂的粒子源分布。2007年，Pozzi等人[33-34]基于MCNP程序开发了MCNP-PoliMi、MCNP-PHOTRACK等程序，其可对探测器的复杂几何结构进行描述且可描述复杂分布的中子源，其中MCNP-PoliMi程序计算的系统响应函数如图3所示[33]，由于其采用耦合计算的策略，后处理的工作量十分巨大。

图3 采用MCNP-PoliMi程序计算的系统响应函数

2014年，Hartwig等人[35-37]建立了基于Geant4程序的有机闪烁体中子物理过程模拟方法，并成功应用于EJ-301有机闪烁体的系统能量响应函数及粒子甄别情况的模拟，模拟结果与实验结果吻合较好，如图4所示[37]。

图4 EJ-301有机闪烁体系统响应Geant4模拟

而在多球谱实验中，随着Monte-Carlo计算方法的发展，采用MCNP和Geant4程序进行多球谱仪系统响应函数计算的研究越来越多，图5(a)、5(b)为Mares等人[22]采用MCNP对不同热中子探测器6LiI(Eu)和3He正比计数管多球谱仪能量响应函数的模拟结果。Geant4程序由于其具备对高能物理过程的模拟能力，近年来研究者们建立了基于Geant4程序进行多球谱仪系统能量响应函数的计算方法，图5(c)为Garny等人[38]采用Geant4程序对10-11～100 MeV能量范围内多球谱仪能量响应函数的模拟。

图5 多球谱仪系统响应函数MCNP模拟以及Geant4模拟结果

与有机闪烁体测量方法、多球谱仪测量方法不同，多箔活化测量方法的能量响应函数为多箔活化材料的中子多群活化截面，能量响应函数的获取本质上为活化材料中子多群活化截面的制作。早在1969年，McElroy等人[26]建立了用于SAND程序解谱的640群活化截面。2008年，中国工程物理研究院的邓勇军等人[39]针对厚活化箔和活化箔包裹热中子吸收材料后多群截面的修正方法开展了相关研究，得到不同厚度(0.048 mm、0.28 mm)Au活化箔640群多群截面和包裹0.5 mm厚度Cd的Au活化箔修正截面，理论和实验符合较好，如图6所示。

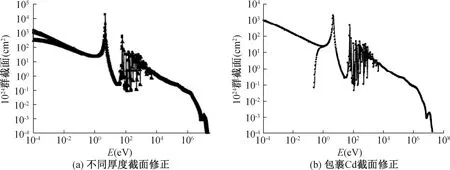
图6 179Au活化箔多群截面修正

1.3 解谱不确定度

中子能谱测量的误差主要来自两方面：一是输入数据的不确定度，二是用于描述物理过程的数学模型近似表示的不确定性以及算法本身缺少唯一解等，一般假设数学模型近似表示的不确定性可以忽略。Manfred Matzke[40]于2002年提出了针对最小二乘法和最大熵方法的中子能谱解谱误差传递方法,最小二乘算法可通过数学推导由先验谱、活化率、截面等信息的协方差数据精确给出中子能谱的不确定度，但该方法限制较多通用性不强，SAND程序的适用性更强，但其中子能谱不确定度相对不完善，通常采用不考虑先验谱的影响和截面协方差的蒙特卡罗抽样方法，或将相关输入量的不确定度按相关性为零的假设进行处理，给出合成不确定度，其他解谱方法的误差处理方式类似。

2009年，王松林等人[41]在采用多箔活化法测量Am-Be中子源屏蔽辐照腔内的中子能谱时，考虑了初始谱引入的误差、解谱所用的截面误差。在活化箔片灵敏区不能覆盖或覆盖较弱的能区，最后的解谱对初始谱有很大的依赖，而在活化箔片灵敏区覆盖较好的能区，最后的解谱对初始谱依赖较小；不同的截面库之间存在微小差异，一般通过选取合适的截面库进行解谱，这部分误差可忽略。

2015年，陈晓亮等人[42]基于广义最小二乘法开发了NSAGLS程序并进行了误差分析，在考虑了输入谱、核反应截面及测量活度不确定度导致的误差后，解谱效果良好。

2016年，李达等人[43]针对SAND-II程序解谱过程提出了一种基于先验谱、活化率和截面协方差的不确定度蒙特卡罗分析方法，首先建立基于线性变换的截面协方差抽样方法，然后利用MCNP计算误差，使用迭代方法估计先验谱的不确定度，最后结合活化率的测量不确定度，利用蒙特卡罗抽样方法计算中子能谱的不确定度，与传统方法计算的不确定度比较接近。

2 主要解谱算法及程序

中子能谱的解谱方法主要有：广义最小二乘算法、奇异值分解和正则化算法、最大熵算法、贝叶斯算法、蒙特卡罗算法、遗传算法、神经网络算法、MLEM算法以及基于压缩感知理论的中子能谱解谱方法，具体情况列于表1。

表1 常用解谱程序介绍

广义最小二乘算法由于发展成熟，目前已有大量解谱程序应用，其他解谱方法由于数学上的复杂性以及发展历史较短的缘故，基于其开发的解谱程序较少，而对于其他一些较新的方法，如神经网络算法以及压缩感知方法，目前研究者们仅对其建立了相应的算法，而未专门开展相关的程序开发。

2.1 广义最小二乘算法

早在1964年，Gold等人[44-45]就提出采用解谱计算值和实验测量值之间的最小二乘偏差作为求解目标，通过迭代策略的设置来保证解的非负性进行中子能谱解谱。

2010—2015年，陈晓亮、孙征等人[46-47]基于广义最小二乘原理对迭代策略进行了修正并开发了程序NSAGLS和2NP。随后Chen等人[42]在有机闪烁体测量实验中采用GRAVEL算法进行了解谱研究，采用GRAVEL程序对测量结果进行了解谱处理，解谱结果与参考解基本吻合,如图7所示。

图7 GRAVEL算法解谱结果

Seghour等人[48-49]在2001年采用SAND-II程序对ANO例题进行了解谱研究，中国工程物理研究院在2014年开展了采用多箔活化方法对中物院某临界装置的中子能谱测量实验，并采用SAND-II程序对测量结果进行了解谱研究，得到不超过2%的偏差，证明了SAND-II解谱的准确度，如图8所示。

图8 SAND-II程序解谱结果

广义最小二乘法通过将计算值和实验测量值之间的最小二乘偏差作为求解目标，从而将中子能谱解谱问题转化为围绕先验值的拟合问题，先验信息通常作为迭代的初值进行使用。目前应用最广的迭代策略为GRAVEL算法，以GRAVEL算法作为核心的解谱程序主要有SAND系列程序，主要包括SANDC、SAND、SAND-II、MSAND等。广义最小二乘解谱算法在有机闪烁体、多球谱仪和多箔活化中子能谱测量实验中进行了广泛的应用，其解谱结果与参考解吻合较好，对于闪烁体解谱的超定问题，该方法对与矩阵病态问题的适应能力尚有提高空间，解谱结果呈现出一定的震荡性；对于多球谱仪以及多箔活化解谱的欠定问题，求解准确程度对迭代的初值依赖性很大。

2.2 最大熵算法

1989年，Weise等人首次将“熵”的概念引入到解谱问题当中[50]，并定义了解谱问题的熵函数，如(2)式所示：

(2)

式中,φDEF为求解中子能谱的先验信息，在最大熵算法中称为预置谱；φj为所求解的中子能谱，其中j为中子能量分段数量；S为所求的熵。

1998年，Reginatto[51]采用基于最大熵算法的MAXED程序对多球谱仪测量结果进行了解谱研究，多球谱仪由8个聚乙烯球组成，对普林斯顿大学等离子物理实验室的托卡马克聚变反应堆装置120 m处中子能谱进行了测量，如图9(a)所示。解谱结果靠近预置谱收敛，但由于测量值与理论值之间存在的偏差，造成解谱结果也与预置谱存在一定的偏差。

Reginatto[52]于2002年针对大气层中～20 km处宇宙射线激发中子的多球谱仪测量结果进行了解谱研究，Green等人[53]于2008年采用MAXED程序对加速器驱动次临界装置的多箔活化测量结果进行了解谱研究并采用MCNP程序对装置中子能谱进行了模拟，祝庆军等人[54]于2014年采用最大熵算法对多球谱仪测量结果开展了解谱研究，雄厚华等人[55]于2018年采用多箔活化方法对聚变包层DFLL-TBM中子能谱进行测量，均证实MAXED程序解谱效果与模拟值吻合较好，如图9(b)、9(c)、9(d)所示。

图9 MAXED程序解谱结果

最大熵算法通过求取约束条件下熵值最大的解来实现解谱，从而将解谱问题转化为优化问题，该方法可以给出非负、连续的中子能谱。最大熵方法在多球谱仪和多箔活化测量结果的解谱中应用较广，其对聚变、裂变以及放射性同位素中子源各种类型的中子能谱也具有较好的适应性。最大熵方法最大的特点为先验信息通过“预置谱”的方式在熵函数构造中进行使用，因此该方法又被认为是先验信息与实测信息相干性最小的解谱方法之一。

2.3 贝叶斯算法

2006年，Reginatto等人[56]又提出基于贝耶斯分析方法进行中子能谱解谱，该方法以贝叶斯理论为基础，将中子能谱解谱问题转化为贝叶斯参数估计问题进行求解，并对多球谱仪测量结果进行解谱研究，解谱结果与Monte-Carlo模拟结果吻合较好，相对偏差通常小于4%，如图10所示。

图10 多球谱仪测量结果贝叶斯解谱结果

2018年，Mazrou等人[47]提出将中子注量率按热区、超热区以及快中子能量区间采用麦克斯韦分布、1/E分布以及瓦特裂变谱的叠加：

φ=φt+φe+φf

(3)

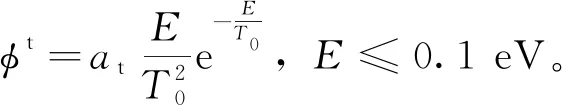
(4)

式中，at、ae、af分别代表热区、超热区、快中子能量区间能量峰的重要性；T0为麦克斯韦分布最可几能量，取0.025 eV；Ed为超热区最低能量，取0.070 7 eV；b和β′分别为控制曲线上升和下降的斜率参数；α和β分别为描述快谱形状和峰值的参数。在他们的研究中采用贝叶斯算法对多球谱仪241Am-Be源中子能谱测量结果进行解谱，如图11所示，采用贝叶斯算法解谱结果与GRAVEL、MAXED等程序结果吻合较好，但在能量峰值上有细微差别，贝叶斯法中该值比MAXED法、GRAVEL法中稍低，这可能与是否设置预置谱和采用不同的解谱方法有关。采用贝叶斯算法解谱结果可以达到较高的精度，解谱结果中子总注量率和剂量率相对偏差小于1%。

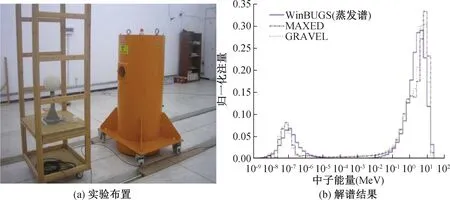
图11 多球谱仪测量241Am-Be源中子能谱

2017年，宋鸿鹄等人[57]采用贝叶斯算法对241Am-Be源中子能谱有机闪烁体测量结果进行了解谱研究，解谱结果如图12所示。在形状上与ISO的标准谱吻合较好，解谱不确定度与实际源的分布、ISO选取有关。

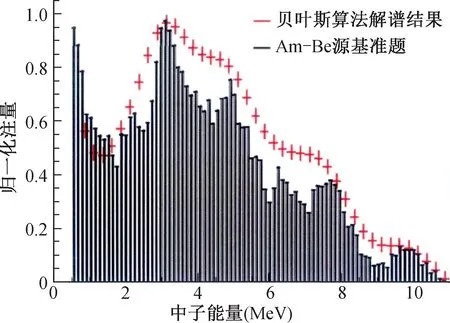
图12 241Am-Be源中子能谱解谱

贝叶斯算法以贝叶斯理论为基础，通过将中子能谱进行参数化表征从而将解谱问题转化为基于贝叶斯理论的参数估计问题，目前的参数化表征方式主要有将中子注量率按热区、超热区以及快中子能量区间采用麦克斯韦分布、1/E分布以及瓦特裂变谱的叠加表征方法。该方法经验性强，在先验较为充分的情况下可以取得比较精确的结果，但目前的参数化表征方式也限定了其使用范围。

2.4 蒙特卡罗算法

2007年，Bedogni等人[58]提出了采用蒙特卡罗算法进行中子能谱解谱。在贝叶斯参数化方法的基础上，增加了蒸发谱和高斯谱模型对快中子能量分布进行表征，增加了蒸发谱对高能区中子能量分布进行表征，代表性的程序为FRUIT。Bedogni等人[59]采用FRUIT程序对241Am-Be源中子能谱、252Cf自发裂变中子能谱、252Cf(D2O)中子能谱、12C离子束碰撞中子源能谱、LINAC放疗中子能谱以及CERF装置中子能谱开展了解谱研究，如图13示。采用蒙特卡罗解谱可以取得较好的解谱效果，解谱结果与参考解吻合较好。对于241Am-Be源中子能谱，解谱结果显得过于光滑，参考解中特征能峰部位有一定的偏差，如图13所示，表明蒙特卡罗算法可以取得较好的解谱精度，其解谱结果总注量率与参考解的最大偏差在5%以内。

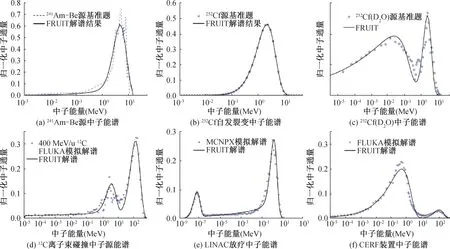
图13 蒙特卡罗解谱方法求解效果

蒙特卡罗中子能谱解谱算法在对中子能谱参数化的基础上，采用蒙特卡罗方法随机生成可表征中子能谱的参数集，然后依据该参数集表征的中子能谱和测量系统的响应函数计算探测器的计数并与实验值进行比较，重复该过程直至满足相应的收敛。该方法的使用具有很强的经验性，其优点为仅需指定中子场类型而无需提供初始能谱，其比较适用于无法通过理论计算获取初始谱的情况。由于采用蒙特卡罗方法作为迭代策略，该方法需要较长的计算时间，另外该方法解谱结果也有可能出现不符合物理意义的结果。

2.5 其他解谱方法

1999年，Freeman等人[60]通过将探测器计数的计算值与实验值差值的平方和作为适应度函数，从而将解谱问题等价为可应用遗传算法进行求解的全局优化问题，然后采用标准遗传算法实现解谱。此后Mukherjee、王东等人[61-65]也进行了相关研究，但该算法始终存在精度较差和能谱不光滑特性。

2002年，Braga等人[66]首次利用神经网络技术对多球谱仪测量结果进行了中子能谱解谱，其采用三层神经网络结构，应用于中子能谱解谱的神经网络结构均比较简单且需要大量样本进行训练，在所求解中子能谱能群数目较少的情况下可以给出比较好的解，但也容易产生“过拟合”或“拟合不足”等学习现象。

2013年，Pehlivanovic等人[67]采用ML-EM算法对特征峰中子能谱、252Cf中子能谱的有机闪烁体测量结果进行了解谱研究，解谱结果与参考解基本吻合，但结果不够平滑，出现了较多不属于参考解的错误峰值，如图14所示。2017年，Molina等人[68]使用ML-EM方法对RECH-1反应堆中子能谱的多箔活化测量结果进行了解谱研究，如图15所示，结果表明在先验信息充足的情况下，ML-EM方法可以取得较好的解谱结果。

图14 闪烁体中子能谱

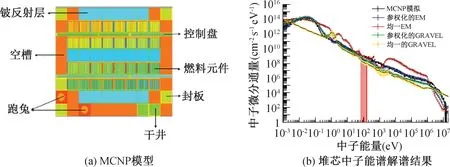
图15 RECH-1反应堆

2004—2006年间由Candes、Romberg和Tao等人[69-73]提出了压缩感知理论，其被认为是对经典采样理论Nyquist-Shannon定理的突破和补充，已广泛应用于信号处理，医学、雷达图像重建，数据压缩、数据传输等领域。刘斌等人[74]于2019年建立了基于压缩感知理论的中子能谱解谱方法，对于核反应堆屏蔽结构典型中子能谱，解谱结果与参考解的总注量率相对偏差在4%以内，如图16所示，对于反应堆辐照监管中多处位置的中子能谱解谱结果与参考解相对偏差小于2%，说明其对高欠定程度的解谱问题也有较好适应性。

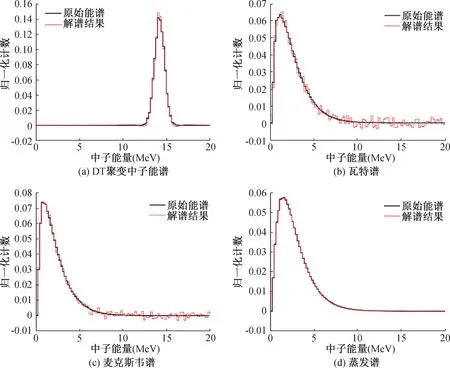
图16 几种典型中子能谱解谱效果

由于研究起步晚，遗传算法、神经网络算法等新兴算法的研究成果还比较少，在解谱稳定性或精度方面不及最小二乘算法等经典算法，但由于新兴算法具有较大的解谱精度和扩展潜力，若能解决现存问题并达到可应用的程度，遗传算法、神经网络算法等将有望在中子能谱解谱中发挥重要作用。

3 总结和展望

文章总结了中子能谱解谱模型、响应函数获取方法，以及解谱过程中的误差产生、处理方法，重点介绍了国内外中子能谱测量技术研究现状以及中子能谱解谱算法研究现状，总结了不同解谱算法的特点，接着介绍了根据不同解谱算法发展的解谱程序，对比了不同解谱算法及程序的优缺点，并推介了目前最适合用于中子能谱解谱的程序。

针对解谱方法的原创性研究国外研究者占大多数，国内学者的研究主要集中在跟踪研究、已有算法应用改进以及依据已有算法开展解谱程序的研发等方面，对于解谱方法本身突破性的研究，尚有较大的提升空间。现有解谱程序主要依赖于发展较早、较成熟的算法开发，基于最小二乘算法的程序最多，包括SAND系列程序、NSAGLS、ANNs等，基于最大熵算法的有MAXED程序，基于蒙特卡罗算法的有FRUIT程序，功能较强、应用最广泛的还属SAND系列程序和MAXED程序。

而对于较新的算法，如贝叶斯算法、正则化算法虽然已有较多研究，解谱效果也一般，尚无通用的程序公开，其他诸如遗传算法、神经网络算法等尚处于原理研究阶段，而遗传算法、神经网络算法具有功能强大、扩展性强的特点，若能解决现在遇到的一些问题，这些新兴算法将在中子能谱解谱中发挥重要作用，这方面还有很多工作可以做，包括解决遗传算法的解谱结果不光滑问题、优化算法提高求解速度等。

经过梳理可发现，目前大多数解谱程序都是采用单一解谱算法，尚无综合多种解谱方法的解谱程序研发，而就目前对解谱效果的调研来看，每种解谱方法对特定的中子能谱类型往往具有适用性，比如ML-EM方法对特征峰类型的能谱往往具有很好的适应性，正则化算法对于平滑的中子能谱具有很好的适应性，尚无对所有中子能谱都有很好适应性的解谱方法。因此，开发包含多种解谱方法的综合性解谱程序具备较强的应用需求，相信随着中子能谱解谱技术的发展，必将在各类核装置的设计和运行、辐射防护剂量学和屏蔽验证以及核军备控制和反恐等领域发挥重要作用。