基于改进UKF算法的锂电池SOC估计

董策勇，李红月

(安徽理工大学 电气与信息工程学院,安徽 淮南 232001)

1 引言

锂电池SOC是电池管理系统(BMS)中的一个重要参数，SOC的精确估计对电动汽车的安全、稳定运行发挥着重要作用[1，2]。然而SOC却无法像电流、电压那样通过传感器直接获得，需要通过特殊的方法进行估计。现阶段，常见的SOC估计方法有：安时积分法[3]、开路电压法[4]、神经网络法[5，6]以及卡尔曼滤波法[7，8]等。其中，安时积分法由于SOC估计时初始值难以确定，导致SOC估计误差不断累积，其精度会随着降低；开路电压法需要把电池静置很长时间，才能获取精确的开路电压值，这种条件在电动汽车实际运行中很难达到；神经网络法需要大量的数据对模型进行训练，但当训练不充分时，SOC估计的精度就会降低。

由于卡尔曼滤波算法(KF)只能解决线性系统问题，国内外研究学者对KF算法进行改进，提出了扩展卡尔曼滤波算法[9，10](EKF)和无迹卡尔曼滤波算法[11](UKF)等非线性系统算法。EKF算法在进行线性化处理时，由于忽略一阶以上的高阶项，引入了线性误差问题，并且还容易造成算法的发散。UKF算法针对线性化方法进行了改进，采用无迹变换求取协方差和均值，避免了线性误差问题，有效地提高了SOC估计的精度[12，13]。但是UKF算法在SOC估计过程中忽略了系统噪声的时变特性，采用固定的系统噪声值，导致了锂电池SOC估计精度较低、稳定性较差[14]。因此，本文采用了Sage-Husa自适应滤波器对系统噪声进行实时估算和修正，再与UKF算法相结合的AUKF算法。

本文基于Thevenin电路等效模型，通过可变遗忘因子最小二乘算法(VFFRLS)对模型参数进行实时辨识，再将参数辨识结果传递给AUKF算法进行SOC的在线估计。最后在UDDS工况对该算法进行了验证。

2 电池模型建立与参数辨识

2.1 电池模型建立

建立锂电池电路等效模型是锂电池SOC估计的重要一步，模型的精度将会直接影响最终SOC估计精度。本文采用如图1所示的Thevenin等效电路模型，相比较于其它模型具有结构简单、计算复杂度低以及SOC估计精度高的特点。

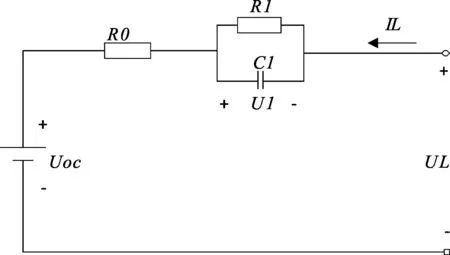
图1 Thevenin等效电路模型

图1中，Uoc为开路电压，R0为欧姆内阻，R1和C1分别表示极化电阻和极化电容，UL为锂电池端电压，IL为电池干路电流。该模型的数学表达式为：

(1)

锂电池SOC的计算表达式为：

(2)

式(2)中，SOC(t)为当前t时刻的值；CN为电池额定容量；I(t)为t时刻电流；SOC(t0)为t0时刻SOC值。

2.2 OCV-SOC拟合曲线

开路电压Uoc和SOC之间有着很强的对应关系，它们的关系曲线在SOC估计中发挥着重要作用。本文以容量为3200 mAh的18650型三元锂电池为研究对象，对该锂电池进行HPPC工况实验来获取OCV-SOC关系曲线。首先对电池充满电，静置1 h以上；采用0.3 C横流放电，每次循环放电10%SOC，直至SOC为0。最后将得到的10组OCV-SOC数据通过MATLAB/Curve Fitting软件进行关系拟合，关系曲线如图2所示。

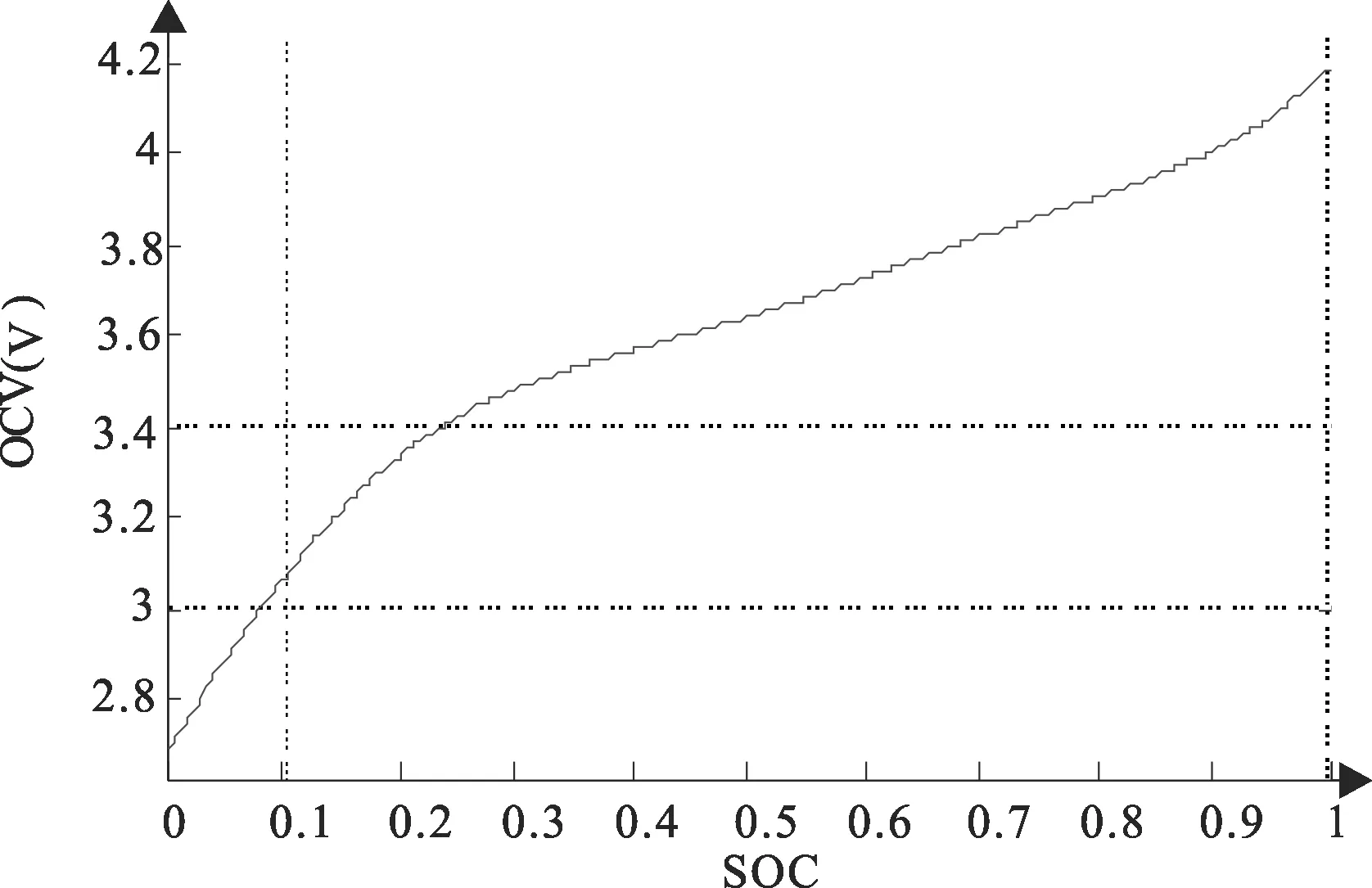
图2 OCV和SOC关系曲线

2.3 基于VFFRLS算法的参数辨识

VFFRLS算法是对RLS算法的改进，可以根据估计误差的大小实时的计算出RLS算法中可变遗忘因子的最优值。可变遗忘因子λ的计算公式如下[15,16]：

(3)

式(3)中，λ(k)为当前时刻的遗忘因子；ρ为敏感因子。λmax、λmin分别为遗忘因子的最大值和最小值；M为窗口大小；ei为i时刻的参数估计误差。

计算出λ值后，再结合RLS算法对锂电池模型参数进行辨识。RLS算法的具体递推公式如下：

(4)

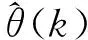
结合VFFRLS算法，对模型表达式(1)进行离散化处理，得到用于锂电池参数辨识的离散化系统方程：

UL(k)=Uoc(k)+a1IL(k)+a2IL(k-1)

+a3[Uoc(k-1)-UL(k-1)]

(5)

式(5)中，a1～a3是用R0，R1和C1表示的参数，通过对a1～a3的反解得到每个时刻R0，R1和C1的参数值，最后再把参数辨识结果传递给AUKF算法进行锂电池的SOC估计。

3 基于AUKF算法的SOC估计

3.1 UKF算法

UKF算法是采用无迹变换(UT)解决了系统噪声的均值和协方差非线性问题。有效克服了无迹卡尔曼滤液(UKF)算法忽略高阶项而导致的精度低，稳定性差的缺陷。

系统的状态方程和测量方程为：

(6)

式(6)中，xk为k时刻的状态向量；wk为系统白噪声；yk为观测向量；vk为测量噪声。

UKF算法估计SOC的具体流程：

流程二：计算k-1时刻的Sigma采样点：

(7)

流程三：状态变量时间更新。

利用步骤(2)获得的Sigma采样点，计算出k时刻状态变量均值和协方差的预测值:

(8)

流程四：测量变量时间更新。计算k时刻观测变量的预测值。

(9)

流程五：协方差与卡尔曼增益矩阵Kk更新。

+Rk

(10)

(11)

(12)

流程六：状态变量和协方差测量更新。

(13)

(14)

将锂电池SOC估计的非线性系统方程(1)和(2)经过离散化处理，应用到上述UKF算法中，从而实现SOC的估计。

3.2 AUKF算法

使用UKF算法对锂电池SOC进行估计时，往往将系统的噪声设定为定值，但是电动汽车实际行驶过程中系统噪声是时变的，不变的系统噪声导致了SOC估计的精度不高。针对以上问题，本文在UKF算法的基础上加入了Sage-Husa自适应滤波器对系统噪声进行实时的估计和校正，以提高SOC的估计精度。Sage-Husa自适应滤波算法对系统噪声的估算如下:

3.2.1 过程噪声均值和协方差的计算

(15)

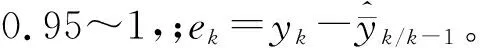
3.2.2 测量噪声均值和协方差的计算

(16)

通过对系统过程噪声和测量噪声自适应更新后，再与UKF算法SOC估计流程相结合，进而提高SOC估计的精度和稳定性。

4 仿真结果与分析

本文选用容量为3200 mAh的18650型三元锂电池作为研究对象。采用UDDS循环工况数据作为验证数据，将UDDS工况数据导入MATLAB软件中，进行AUKF算法的精度验证，并与UKF算法对比。SOC初始值设定为0.8，实际初始值为1，采样间隔为0.1s。图3为两种估计算法的SOC估计结果对比图，图4为SOC估计误差对比图。

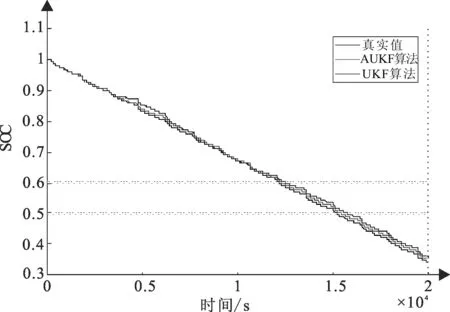
图3 SOC估计结果对比

由图3的SOC估计结果可以看出AUKF算法比UKF算法更加逼近SOC真实值。由图4的SOC误差对比可以看出AUKF算法明显优于UKF，具有更好的估计精度和稳定性。为了更直观体现2种SOC算法的估计效果，本文选取SOC平均误差与SOC最大误差作为评价指标，如表1所示。

图4 SOC误差对比

由表1数据对比可知，AUKF的SOC最大误差与SOC平均误差均比UKF算法小。相比较与UKF算法，AUKF算法SOC精度提高了1.04%。充分验证了AUKF算法的精确性和稳定性。

表1 2种算法的SOC估计误差对比 %

5 结论与讨论

本文为提高UKF算法的SOC估计精度，利用Sage-Husa自适应滤波器对系统噪声进行实时估算和修正，形成AUKF算法。基于Thevenin等效电路模型，利用VFFRLS算法对等效模型参数进行辨识，再把参数辨识结果传递给AUKF算法进行SOC估计。通过仿真结果对比，验证了AUKF算法的SOC估计能力要优于UKF算法，SOC估计精度提升了超1%，具有更好的精确性和收敛性。