层理灰岩抗拉力学参数各向异性及破裂特征分析
黄 殷 婷,左 双 英,钟 帅,刘 博
(1.贵州大学 资源与环境工程学院,贵州 贵阳 550025; 2.贵州大学 喀斯特地质资源与环境教育部重点实验室,贵州 贵阳 550025)
0 引 言
岩体内部存在的层理、节理、裂隙等结构面导致了其具有明显的各向异性[1]。同时试验研究和工程实践表明层状岩体在荷载作用下的侧向变形及破裂与张拉裂纹的累积和扩展密切相关,常常表现为拉破坏,严重危及到边坡、基坑、洞室顶板、高位危岩体处置等工程的安全[2-4],因此,开展岩体在受拉状态下各向异性力学特性及破裂特征研究具有重要意义。
巴西劈裂试验是测试岩石抗拉强度的间接拉伸方法之一,国内外学者利用巴西劈裂试验开展了一系列岩体抗拉各向异性的研究。刘运思等[5]结合单弱面理论,对板岩进行巴西劈裂试验,建立了抗拉强度与层理倾角之间的关系式,发现板岩抗拉强度随层理倾角增大而减小。Dan等[6]对砂岩、片麻岩、板岩进行巴西劈裂试验,研究层理倾角、加载方向角对抗拉强度和破坏模式的影响。Abbass等[7]研究发现,随着层理倾角的增大,板岩抗拉强度、裂缝长度和圆盘试样破坏所需的能耗逐渐降低。武鹏飞[8]、许多等[9]对煤岩进行了劈裂试验,发现沿垂直层理方向进行加载裂纹更易传播与扩展。杨志鹏等[10]针对页岩做了劈裂试验,发现随层理倾角增加,页岩试件破裂产状由直线型向曲弧形过渡。钟帅等[11-12]对7组不同角度层理灰岩进行巴西劈裂试验,根据岩石声发射累计振铃次数定义拉裂损伤变量,推导了抗拉强度、劈裂模量及损伤变量随层理倾角的变化规律,并建立了横观各向同性本构关系。
三维激光扫描技术能精确提取扫描对象三维空间坐标数据,部分学者通过扫描岩体破裂面,对细观破裂面形态及结构面统计参数进行了研究。黄达等[13]结合三维激光扫描与扫描电镜技术,发现三轴高应力条件下卸荷破裂的大理岩破裂面细微观断裂性质与围压的卸荷速率和初始应力状态密切相关。陈珺等[14]对黑砂岩进行直接拉伸与拉伸剪切试验,通三维扫描技术,总结了拉应力下岩石破裂面粗糙度随应力状态的变化规律,探讨了不同破裂机制对破裂面形貌的影响。而粗糙度作为评估结构面起伏程度的参数之一,常用来定量评价拉裂与剪切破坏状态。彭守建等[15]发现采用粗糙度JRC评价结构面各向异性时,劈裂断裂结构面与剪切断裂结构面各向异性差异较大。陈世江等[16]则通过比较已有结构面粗糙度的定量表征方法,发现分形维数是结构面粗糙度定量描述的有效方法。
以上研究成果主要展现了层状岩体抗拉力学特性及破坏裂缝走向与层理倾角有强烈相关性,也针对单一结构面不同区域粗糙度量化参数进行了评价与比较,但对于在巴西劈裂试验条件下受层理结构影响的破裂面各向异性特征及定量化研究较少涉及。因此,本文基于不同层理倾角灰岩的巴西劈裂试验,研究层理倾角对应力-应变曲线的影响以及灰岩力学参数的各向异性特征,观测灰岩宏-细观破坏形态与裂缝扩展过程,利用三维激光扫描技术与结构面粗糙度量化参数,对不同层理倾角灰岩破裂面内部发展过程与力学演化机制进行综合探讨,为进一步完善层状岩体张拉破坏内部演化机制研究提供参考。
1 试验方案
1.1 试样材料
试验岩样为三叠系大冶组中风化中厚层状灰岩。将层理面与水平面夹角θ定义为层理角倾角,钻取直径50 mm、厚度25 mm的试样块并进行端面研磨,保证上下两端平行度在±0.05 mm以内,表面平整度控制在±0.03 mm以内,所有试样均在室温干燥环境中保存。每个角度3个试样,共21个试样,部分样品如图1所示。
1.2 试验设备及方法
本次试验采用WAW-1000kN型微机控制电液伺服万能试验机对试样进行加载。DH3818静态应变数据采集仪记录加载过程中岩体的累积应变值。试样表面前后对称,布置两条长20 mm、宽3 mm的应变片(见图2),设定压力机加载速率为0.05 kN/s。
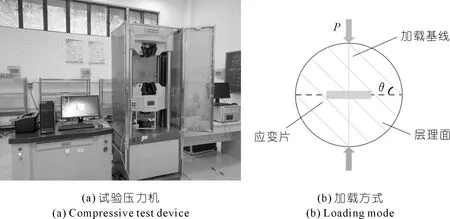
图2 试验仪器及加载方式示意Fig.2 Schematic diagram of test instrument and loading mode
为了定量分析不同层理倾角巴西劈裂试验过程中破裂面的细观结构特征变化规律,本文采用福建锐品科技有限公司出品的高精度三维激光扫描仪对岩样的主破裂面进行扫描测试。扫描仪由两个ONSEMI工业测量传感器(363万像素,1280×800)、结构光栅发生器以及支架组成,如图3所示。扫描仪单帧精度可达±0.04 mm,扫描速度≤0.3 s,利用该扫描仪可对岩样破裂面进行多视角测量并进行全自动拼接,可轻松获取高精度表面三维数据与纹理信息,真实展示破裂面形貌特征,为进一步参数计算提供数据支持。

图3 三维扫描仪器设备Fig.3 3D laser scanner
2 不同倾角层理灰岩抗拉力学参数各向异性分析
2.1 拉应力-应变曲线
试验过程中,可以采集到圆盘试件的竖向荷载,计算出岩石的水平拉应力[17]:
(1)
式中:P为任意时刻的竖向荷载,kN;D为圆盘直径,mm;t为圆盘厚度,mm。当P达到最大值时,σmax即为抗拉强度。
绘制水平拉应力-应变曲线如图4所示。可以观察到各个层理倾角岩样对应的应力-应变曲线差异较大,但总体仍表现出孔隙压密、弹性变形和破坏3个阶段。加载初期,由于灰岩内部存在孔隙或微裂缝,试样表面与加载板接触后先产生了局部压密变形,随后很快进入弹性变形阶段,随着荷载增大,变形曲线近似呈直线上升趋势。应力随着应变的增加到达峰值后,试样发生破坏,应力-应变曲线陡降,应力值近乎垂直于横向坐标轴发生跌落,而灰岩试样脆性较强导致破坏在瞬间产生,部分试样飞溅,所以无明显的峰后曲线。
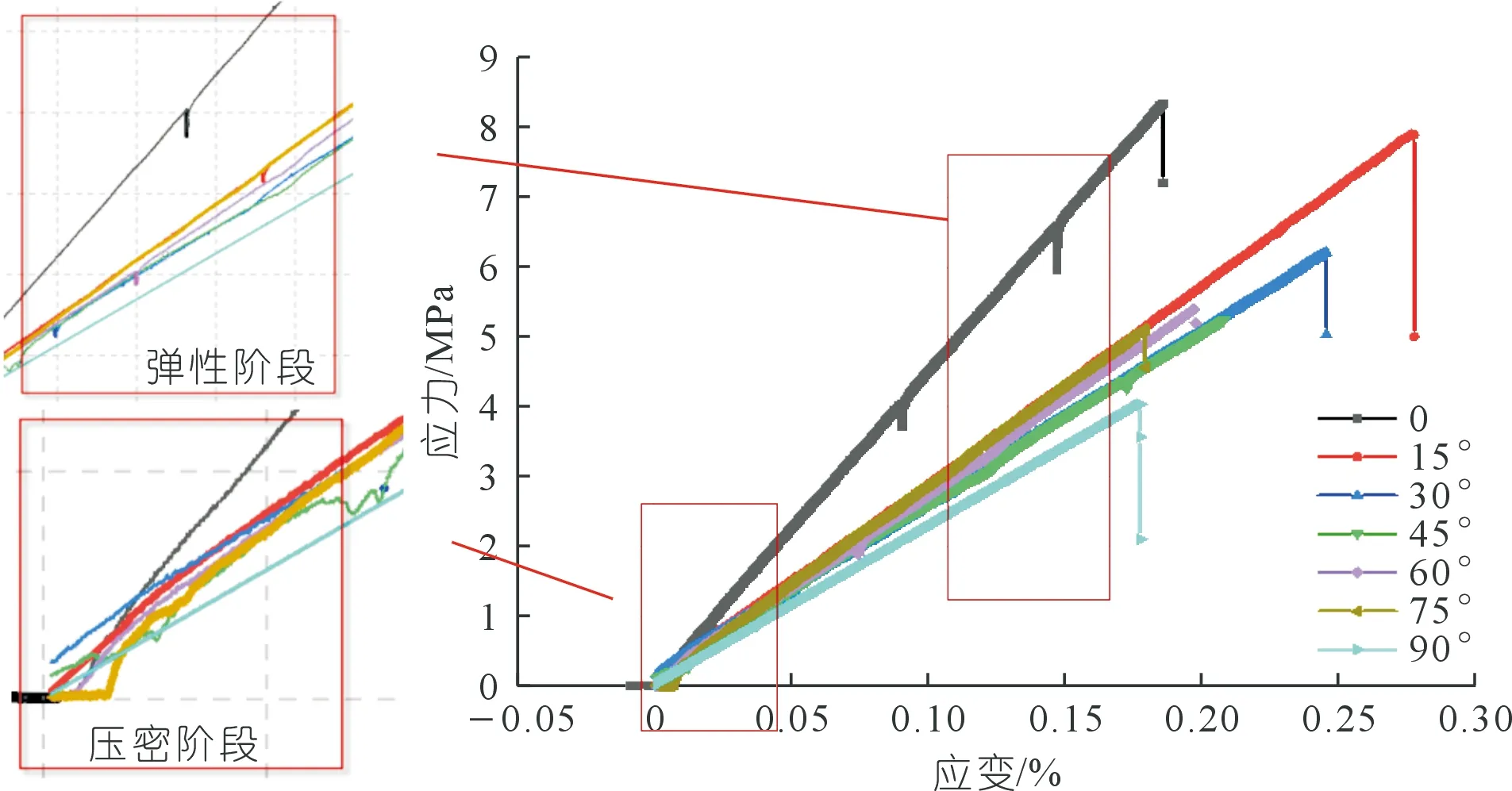
图4 灰岩试样典型拉应力-应变曲线Fig.4 Typical tensile stress-strain curves of limestone samples
对于含层理灰岩,采用宫凤强等[18]推导的公式计算拉伸模量:
(2)
式中:Pt为破坏荷载,kN;Δut为最终拉伸长度,mm。
2.2 抗拉力学参数各向异性分析
对不同层理倾角灰岩的巴西劈裂试验结果进行处理,得到每组试样抗拉强度与拉伸模量平均值,并依据结果计算出每组试样泊松比,绘制岩样力学参数与各层理倾角之间的关系曲线,如图5所示。
由图5(a)对比分析可知,随着层理倾角的增大,岩石试样抗拉强度与拉伸模量整体呈现下降趋势,其中拉伸模量在30°~60°范围内随层理倾角的增加曲线斜率由小变大,而抗拉强度的曲线斜率则反之。如图5(b)所示,泊松比整体则随层理倾角的增大呈上升趋势,在90°时最大,为0.259;峰值应变则在层理倾角为15°时达到峰值,为0.278,之后随倾角的继续增大呈减小的趋势,在90°时最小,为0.178。
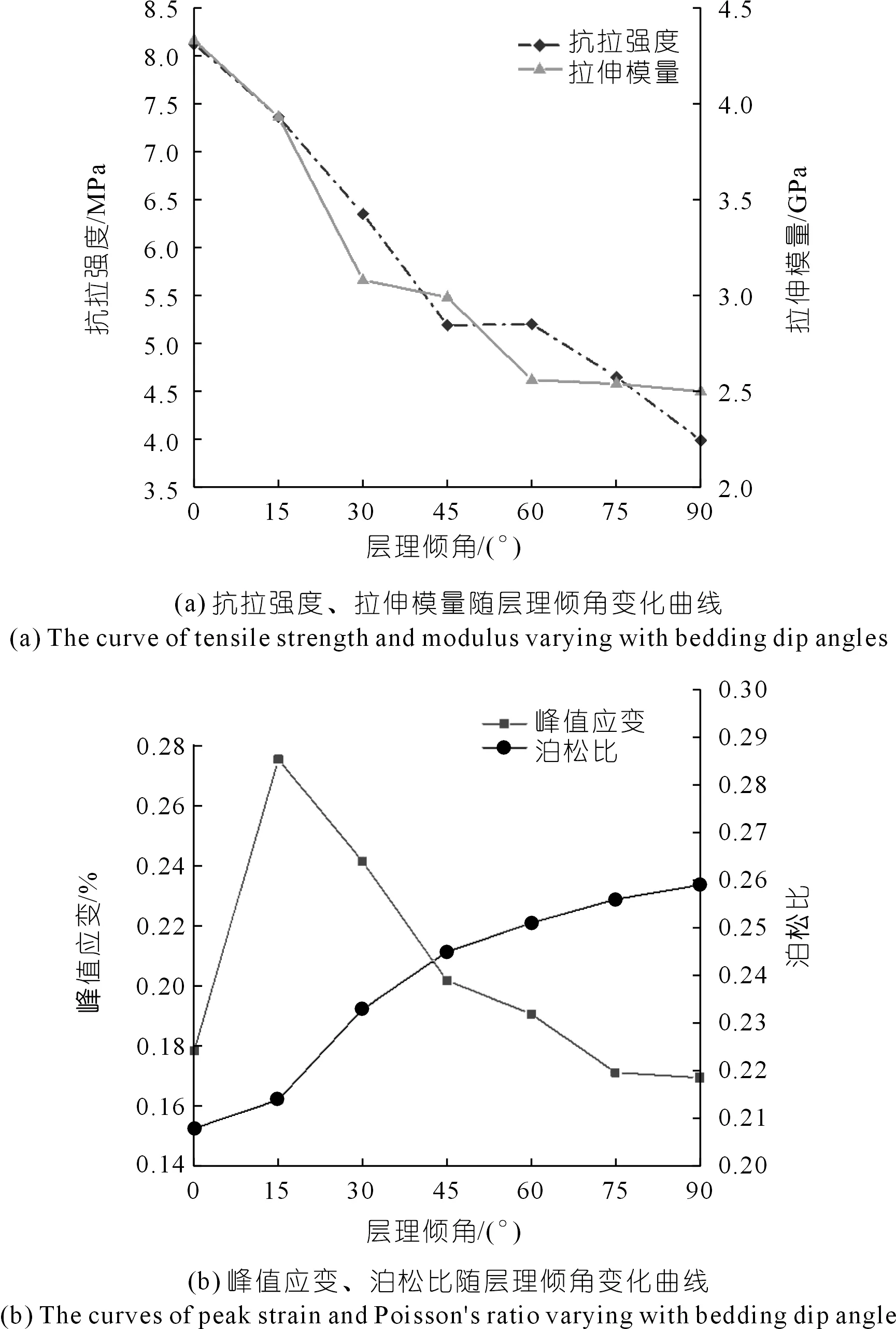
图5 典型灰岩试样力学参数随层理倾角变化曲线Fig.5 Curves of mechanical parameters varying with bedding dip angle
为了表征层理倾角对各力学参数各向异性影响的程度,引入各向异性度参数α(θ),表示不同层理倾角灰岩力学参数与水平层理(θ=0)力学参数对比的降低幅度,即:
(3)
式中:ζ(θ)为不同层理倾角的力学参数,如抗拉强度、拉伸模量等;ζ(0)为层理倾角为0时的力学参数。
α(θ)越大,表明岩样力学参数受层理倾角影响越大,各向异性特征、层理结构效应越明显。按照式(3)计算,不同层理倾角灰岩的力学参数各向异性度变化曲线如图6所示。
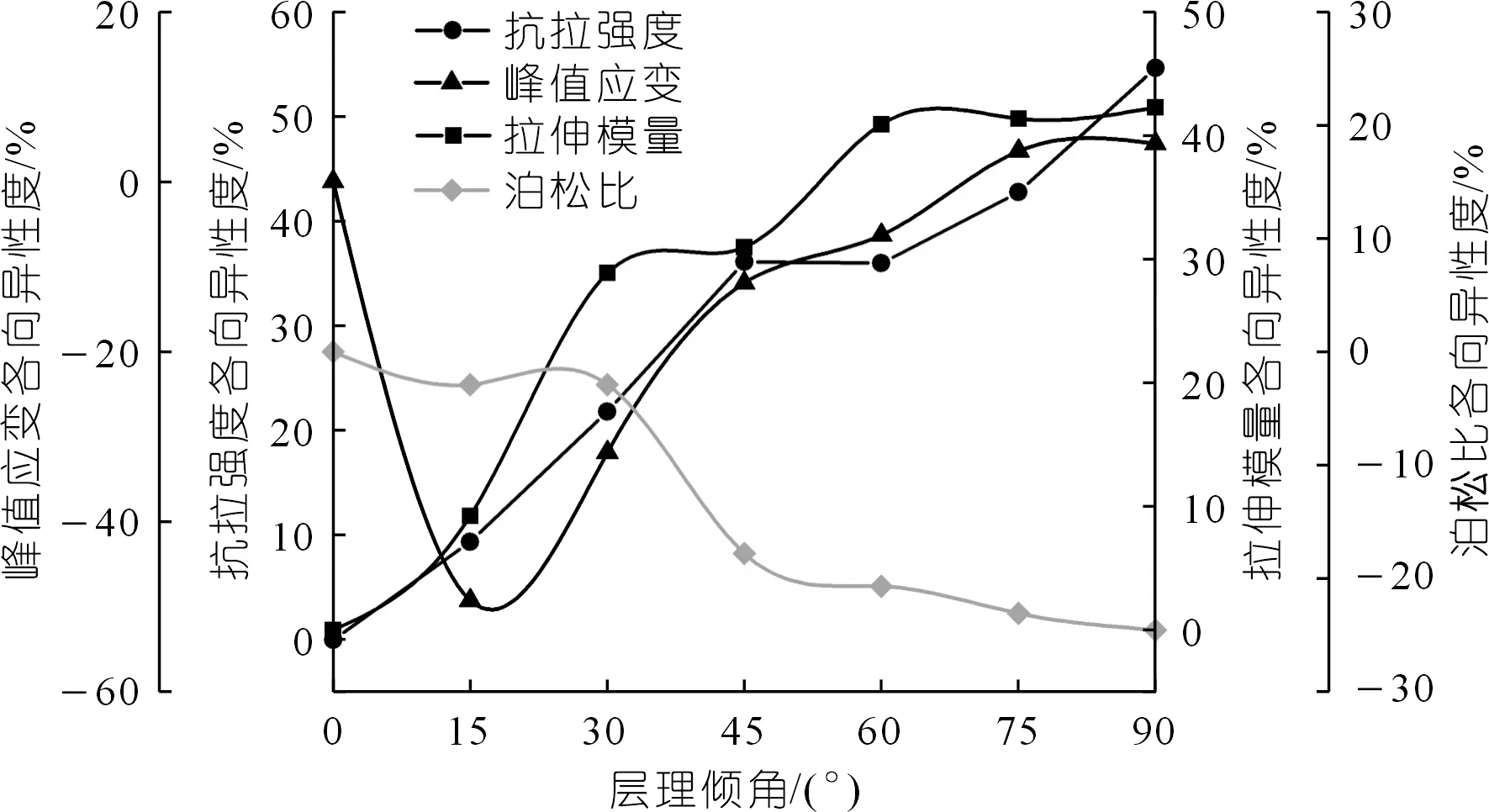
图6 力学参数各向异性度曲线Fig.6 Curves of anisotropic mechanical parameters
从图6中可以观察到:随着层理倾角的增加,抗拉强度和拉伸模量各向异性度曲线逐渐上升,在90°达到最大,相对于0°,增量分别约为55%,42%;泊松比各向异性度曲线随着层理倾角增大呈负增长趋势,也在90°时达到最大,相对于0°,增量约为25%;而峰值应变各向异性度(绝对值)在层理倾角为15°时达到最大50%,随后逐渐减小。这表明层理倾角对各个力学指标均有影响,其中对抗拉强度和拉伸模量影响最大。
3 宏-细观破坏形式及机制分析
3.1 宏观破坏形态各向异性
将不同层理倾角的典型试样加载过程中形成的宏观裂隙进行统计与素描,如图7所示。从裂隙整体形态来看,破裂形态以张拉为主,部分出现沿层理剪切,主裂缝扩展方向与试件所受最大主应力方向一致。当层理倾角为0时,应力垂直于层理方向,抑制了试样沿层理方向滑移破坏的发生,主裂缝受到拉应力作用穿过圆盘中心向两端延伸,最终贯通形成垂直于层理方向的“直线”状裂缝,为劈裂破坏,并且由于加载两端产生应力集中,所以加载点附近的岩样出现次生裂缝,部分岩体碎屑掉落。此时测得的抗拉强度可以认为是灰岩基质体的抗拉强度,因此θ=0°时的抗拉强度值为最大值。当层理倾角θ=15°~30°时,裂缝呈“月牙形”,即岩石样品中间的裂缝向侧面凸出。这是因为随着层理倾角逐渐增大,虽然主裂缝仍沿加载点起裂,以张拉破坏为主,但因受到薄弱层理面与矿物成分的影响,局部有剪切破坏产生,这也导致裂缝偏离圆盘中心扩展,且有沿层理方向发展的趋势。当层理倾角θ=45°~60°时,主裂缝沿弱面层理方向剪切型直线扩展,在圆盘中心位置有局部次生张拉破坏。当层理倾角θ=60°~75°时,裂缝扩展方向愈加接近于层理弱面,这会导致抗拉强度进一步降低。当θ=90°时,虽然加载方向与层理面方向一致,但是加载点处无临空剪出口,试样沿层理弱面发生张拉破坏,此时所测抗拉强度本质是层理弱面的抗拉强度,故此时的抗拉强度最小。
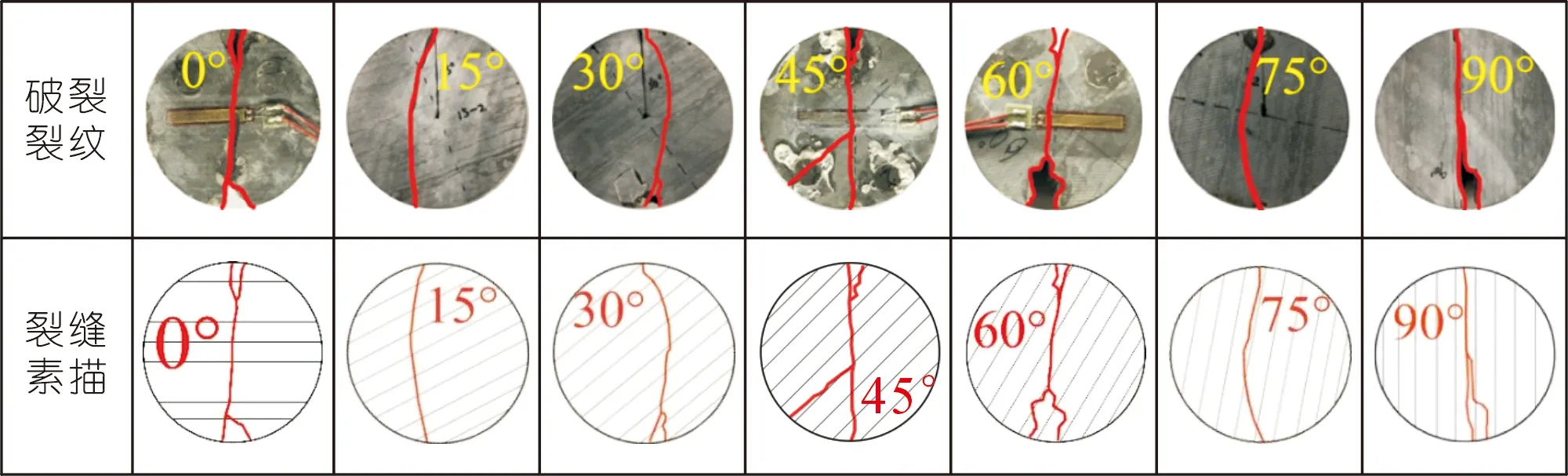
图7 岩石破坏裂纹扩展图Fig.7 Crack propagation diagram of rock failure
3.2 破裂面细观特征各向异性
将0,15°,30°,45°,60°,75°,90°等7种倾角的灰岩进行巴西劈裂试验后,取其正、反典型破裂面进行高精度三维扫描,获得7组点云数据,并用Geomagic系列软件对扫描面进行平滑、降噪与封装,提取坐标并导入Surfer 12中进行处理,生成的不同层理倾角灰岩正、反破裂面三维数字图像如图8所示。

图8 不同倾角典型岩样破裂示意Fig.8 Schematic diagram of crack plane with different dip angle
当层理倾角θ=0°时,因加载点处出现小范围的应力集中而导致试样发生局部到整体的张拉破坏,破裂面受力边缘处比中间略显粗糙。θ=15°~30°时,岩样发生部分剪切破坏,破裂面较θ=0°时平滑,正反两块岩样破裂面凹凸起伏基本吻合,沿中心线部分岩体高于两侧岩体,这是由于岩样受力范围较小,先沿加载中心线方向发生张拉破坏,随后再向两侧沿薄弱结构面发生剪切扩展,岩样剖面呈“月牙形”。层理倾角θ=45°时,破裂面粗糙,并且正反破裂面吻合度较低,起伏程度及凹凸位置均不相同。如反向破裂面右扫描图所示,破裂面下缘呈台阶状,中部破裂面较为破碎,试验后可观察到较多岩石碎块从岩样上掉落。分析原因是由于此时发生的破坏不仅是层理面与灰岩基质体的拉伸-剪切破坏,还存在裂缝在发展过程中因局部应力产生的二次张拉破坏,多种破坏同时作用导致岩样呈破碎状。当层理倾角θ=60°~75°时,受到剪切-拉伸作用的影响,岩样剖面呈“弧形”,且如正反破裂面扫描图所示,因为层理面作为岩体的薄弱结构面,黏聚力较低,所以当破坏平行于层理面产生时,破裂面较为光滑。层理倾角θ=90°时,加载方向与层理面方向平行,裂缝沿最薄弱层理面产生张拉破坏,受层理面内充填矿物成分影响,破裂面又变粗糙。
3.3 破裂面结构量化参数各向异性
3.3.1节理线粗糙度系数
Barton[19]在1973年首次提出节理粗糙度系数JRC的概念后,相关学者通过大量试验与研究给出了10条典型节理轮廓线,根据结构面粗糙程度将JRC值定义在10~20数值范围内,此方法在工程实践中得到了广泛应用。但由于此方法是基于人工观察对粗糙度进行的大致估计,受主观性影响较大,故采用Gentier等[20]提出的裂隙面粗糙度的经验模型,通过建立投影面积与实际面积的联系,对不同层理倾角灰岩破裂面线粗糙度进行计算。本次试验定义破裂面切口面积为截面面积,又因试验采用了统一直径为50 mm、厚度为25 mm的试样,故定义标准截面面积1 250 mm2。通过三维扫描仪获取点云数据,并对不同层理倾角下岩样断裂面面积进行数值化处理后获得不同层理倾角破裂面实际表面积,以式(4)进行计算:
(4)
式中:RL为裂隙的线粗糙度,无量纲,与破裂面粗糙程度呈正相关;RA为粗糙裂隙面实际面积与裂隙面投影面积之比。
3.3.2粗糙度分形维数
自Mandelbrot将分形几何运用于岩体结构面粗糙度系数研究以来[21],分形理论逐渐成为处理复杂系统的有力工具,而盒维数法在粗糙度分形理论中有着广泛的应用[22]。使用边长为ε的立方体盒子依次覆盖试样破裂面表面,N(ε)为覆盖试样破裂面所需要的边长为ε的立方体个数,得到:
N=ε-D
(5)
式(5)等号两边取对数,可得:
lgN=-Dlgε
(6)
取不同尺寸的ε,其对应的N(ε)是恒定的,将两者用最小二乘法拟合成直线,直线斜率的相反数即为该破裂面粗糙度盒维数,即:
(7)
式中:ε为立方体的边长;N(ε)为破裂面被覆盖所需的边长为ε的立方体个数;DB为破裂面粗糙度盒维数。
试样破裂面越粗糙,起伏程度越大,覆盖破裂面需要的盒子数就越多,所得粗糙度盒维数就越大。在巴西劈裂试验条件下,选取不同层理倾角灰岩破裂面进行三维激光扫描,通过MATLAB编写盒维数算法对扫描数据进行处理,使破裂面三维成像并置于一平面上,将平面用网格进行划分,然后用不同边长εi的立方体盒子去覆盖三维破裂面,程序中将盒子尺寸设置为2n(mm)依次进行覆盖,覆盖过程如图9所示
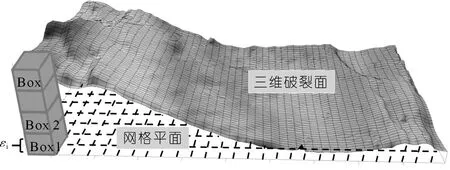
图9 盒维数计算示意Fig.9 Schematic diagram of box dimension calculation
计算不同层理倾角灰岩线粗糙度与盒维数值结果如表1所列,绘制结构面量化参数各向异性曲线如图10所示,两者随着层理倾角的增大变化趋势基本一致。
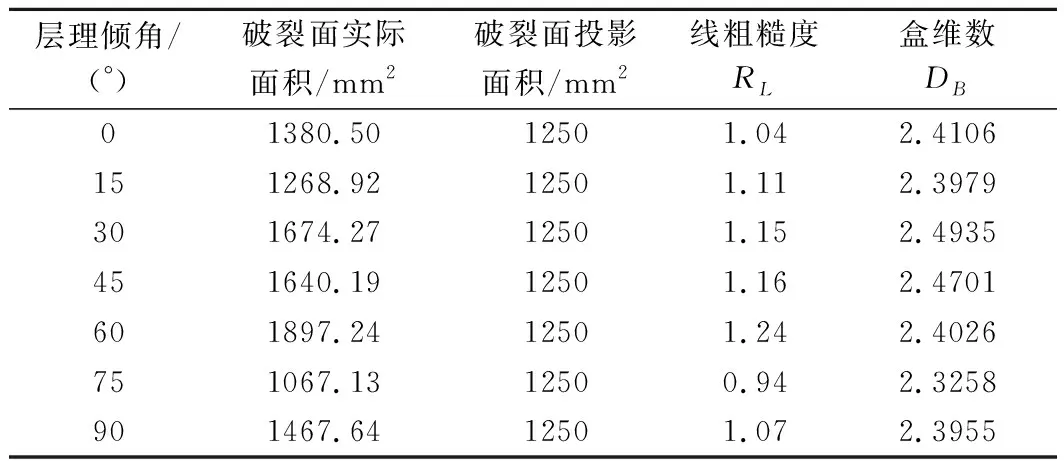
表1 不同层理倾角灰岩结构面量化参数
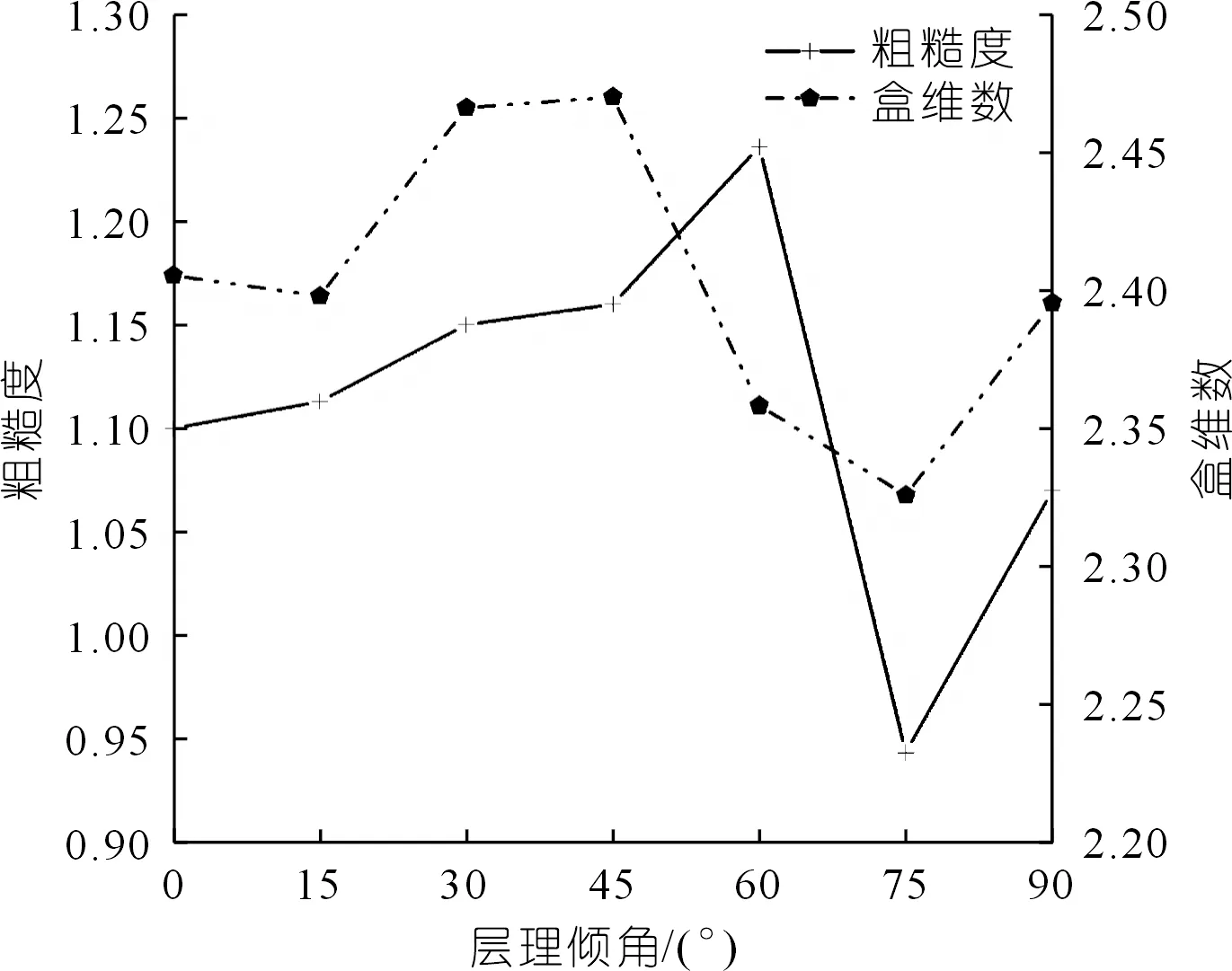
图10 结构面量化参数各向异性系数对比曲线Fig.10 Comparison curve of anisotropy coefficient of quantitative parameters of discontinuity
层理倾角θ=0°时的结构面量化参数均大于层理倾角θ=90°时的对应参数,即层理倾角θ=90°的破裂面较层理倾角θ=0°时的破裂面光滑。这是因为当层理倾角θ=0°时,试样裂缝贯通灰岩基质体,拉应力由灰岩基质体承担,而θ=90°时试样是沿层理弱面发生张拉破坏,因层理弱面强度较小发生张拉破坏时裂缝扩展所受阻力更小,破裂面更光滑。就盒维数随层理倾角变化曲线而言,DB(θ=0°)略大于DB(θ=15°),这是因为θ=15°时的岩样破坏模式开始受到层理倾角的影响,开始有局部的剪切破坏产生,破裂面的部分凸起体被剪切磨平,粗糙度开始降低。当层理倾角θ=30°~45°时,由加载点施加的轴向应力分解为沿层理面的剪应力与沿加载中心线的法向应力,虽然此时仍以拉伸破坏为主导并伴随局部的剪切破坏,但随着破坏的进一步发展,应力分配不断变化,破裂面变化情况复杂,破裂面如洼地等起伏形态增多,所需要覆盖破裂面的盒子数变多,DB变大。当层理倾角θ=60°~75°时,随着层理面逐渐倾向于加载中心线,沿层理面剪应力逐渐增大,裂缝路径逐渐沿层理方向扩展,大量破裂面凸起体逐渐从被剪短磨损进入剪切滑移阶段,破裂面光滑部分增多,盒维数减少。当层理倾角θ=90°时发生层理面张拉破坏,此时破裂面的粗糙程度又有所增大,因此曲线又反向增大,这是由层理弱面矿物成分等因素决定的。
整体而言,盒维数DB的变化趋势与宏-细观破裂特征较符合,随着层理倾角的增大,盒维数在θ=30°~45°达到峰值后逐渐减小,这说明拉-剪复合作用下破裂面破坏状况较复杂,随着裂缝路径逐渐偏向层理倾角,剪切破坏起主导作用,破裂面逐渐变得平滑。线粗糙度RL整体走势虽与盒维数DB相近,随层理倾角的变化呈先增大后减小的趋势,但相较于盒维数DB在θ=45°达到峰值,线粗糙度RL则于θ=75°时达到峰值,并且在层理倾角θ=0°~45°时,RL逐步增大,并未如盒维数DB一般在θ=15°出现小幅减小的情况。笔者认为这是由于θ=15°~30°,θ=45°~70°时,岩样剖面呈“弧形”或“月牙形”,由线粗糙度定义可知,破裂面曲度会对线粗糙度值产生一定影响,因此发现相较于线粗糙度,盒维数能更好地量化反映灰岩破裂面粗糙程度随层理倾角的变化规律,可为研究破裂面之间的差异特征提供有效手段。
4 结 论
针对不同层理倾角灰岩开展了巴西劈裂试验研究,对层理灰岩力学参数各向异性特征进行了比较分析,利用三维扫描技术对宏观破裂形态与细观破裂特征进行了总结与量化统计,得到以下主要结论:
(1) 层理灰岩抗拉力学特性具有明显的各向异性,通过各向异性度比较发现,抗拉强度与拉伸模量受层理倾角影响较强烈,两者随层理倾角的增大呈减小的趋势。当θ=0时,抗拉强度与拉伸模量最大,分别为8.12 MPa和4.33 GPa,这是灰岩基质体的力学参数。当θ=90°时,抗拉强度与拉伸模量最小,分别为3.99 MPa和2.50 GPa,这是灰岩层理弱面的力学参数。
(2) 灰岩的宏观破坏裂缝可分为3种典型形态:直线型、月牙形、弧形。当层理倾角θ=0,90°时宏观裂缝均呈“直线型”的张拉破坏;当层理倾角15°≤θ≤30°时,宏观裂缝呈“月牙形”,岩样中间的裂缝向一侧突出,此时有局部剪切破坏产生;当层理倾角45°≤θ≤75°时,宏观裂缝呈“弧形”,属于拉-剪复合破坏形态,次生裂缝发育丰富。
(3) 通过三维激光扫描技术对破裂面进行数字化处理,采用RL,DB两种结构面量化参数评价破裂面粗糙程度,发现层状岩体破裂面粗糙程度也具有明显的各向异性:在θ=0°~90°区间内,粗糙程度整体呈先增大后减小的趋势,破裂面张拉作用越强,起伏粗糙度越大,剪切作用越强,起伏粗糙度越低。而通过比较结构面量化参数RL,DB发现,盒维数DB各向异性特征较明显,能较好反映不同层理倾角破裂面之间的差异特征,线粗糙度则受试样剖面曲度因素影响较大。

