基于GR4J-LSTM混合模型的洪水预报研究

崔 震，郭 生 练，王 俊，王 何 予，尹 家 波，巴 欢 欢

(1.武汉大学 水资源与水电工程科学国家重点实验室，湖北 武汉 430072； 2.长江勘测规划设计研究有限责任公司，湖北 武汉 430010)

0 引 言

准确的洪水预报对水库运行管理至关重要，同时对于预报工作者更是一项重大的挑战[1]。水文模型可以概化复杂的水文现象和过程，因此洪水预报通常基于水文模型，以降水、蒸发等水文要素为依据判断径流响应。从反映水文运动物理规律的科学性和复杂性程度而言，水文模型主要分为3类：概念性模型、物理模型和数据驱动模型(黑箱子模型)[2]。概念性模型使用较简单的物理概念和经验公式(如蒸发公式、汇流单位线等)或含有物理意义的结构单元(如线性水库、线性河段等)，构成一个系统来近似地描述流域水文过程，其可操作性较强，近年来被广泛应用[3]。例如，Perrin等[4]开发的GR4J (modèle du Génie Rural à 4 paramètres Journalier)模型仅采用4个参数描述产汇流过程，国内外学者在多个流域验证了其具有良好的降雨径流模拟效果[5]。由于降雨径流转化过程极其复杂，其非线性和非稳态特征使水文模拟及预报工作充满不同来源的不确定性，这导致概念性水文模型难以保持准确的多时段过程预报[6]。数据驱动模型被证实能够有效处理非线性、非稳态特征的数据集[7]，其中最具代表性的是人工神经网络(Artificial Neural Network，ANN)。近年来，随着计算机硬件条件和网络算法的迅速发展，深度学习(Deep Learning)技术在各个领域得到广泛应用[8]。Hochreiter等[9]提出了长短时记忆神经网络(Long Short-Term Memory Neural Network，LSTM)，因其克服了循环神经网络(Recurrent Neural Network，RNN)中梯度爆炸或消失等问题而得到众多关注[10]。单输出的LSTM神经网络能够较好地模拟洪水过程和处理一定程度的噪声[11]，但不能考虑降雨径流转化机制，并常受输入变量可获得性的限制，存在较长预见期的预报精度偏低等问题，故在实际预报业务中应用较少。

为了提高水文模型的预报精度，水文学家做了大量研究，比如预处理方法(小波转换[12]，奇异谱频分析法[13]等)和后处理方法(卡尔曼滤波法[14]，贝叶斯平均法[15]等)。其中，将概念性水文模型的输出作为ANNs的输入是提高洪水预报精度的一个新思路。Pang等[16]建立了基于ANN的非线性扰动模型(Nonlinear Perturbation Model，NLPM)，用ANN代替线性响应函数，模拟未知的输入扰动和输出扰动间的关系，定义为NLPM-ANN，提高了降雨-径流预报的效率和准确性。Ren等[17]在高寒地区将HBV模型生成的积雪融化和冰川融化径流输入到贝叶斯神经网络(Bayesian Neural Network，BNN)中，建立了适用于高寒地区的径流预报模型，不仅能够提供更精确的径流预报，还可以生成合理的不确定性区间。Young等[18]使用HEC-HMS模型的模拟流量作为反向传播神经网络(Backpropagation Neural Network，BPNN)和支持向量回归(Support Vector Regression，SVR)的额外输入，结果表明两种混合模型均能够提高HEC-HMS模型的模拟精度。目前，探讨概念性水文模型和LSTM神经网络混合模型的文献不仅相对较少，而且未能结合实际的预报降水资料进行研究，更无法从模型内部解释混合模型模拟精度提高的机理。

基于上述研究，本文结合GR4J模型和LSTM神经网络的优点，建立GR4J-LSTM混合模型，并结合欧洲中期天气预报中心(European Centre for Medium-Range Weather Forecasts，ECMWF)的3 h预报降水产品，将GR4J模型的预报流量以补充神经网络输入变量的策略耦合到LSTM神经网络中，并在陆水水库入库流量的多时段过程预报中检验混合模型的有效性，最后采用平均影响值(MIV)算法评估输入变量的相对重要性。

1 模型和方法

1.1 GR4J模型简介

GR4J模型为集总式概念性水文模型，仅含有4个参数，分别为：产流水库容量(X1)、地下水交换系数(X2)、汇流水库容量(X3)和单位线汇流时间(X4)。该模型采用产流水库、汇流水库两个非线性水库进行产汇流计算[5]。本文以纳什效率系数(NSE)为目标函数，采用SCE-UA算法率定GR4J模型参数，具体公式见文献[19]。

1.2 LSTM神经网络

LSTM神经网络是一种特殊的RNN神经网络。LSTM与其他神经网络的区别在于LSTM中的隐藏层由内部自循环单元组成[7]，能够克服RNN在时间反向传播(Backpropagation Through Time，BPTT)算法中容易出现的梯度爆炸或消失等问题。因此，LSTM在处理各种时间序列的预测方面具有良好的适用性。LSTM通常由输入层、隐藏层和输出层组成全连接神经网络。为消除样本量纲的影响，需首先对样本数据归一化，再采用Adam算法训练模型和Sigmoid函数计算隐藏层和输出层的输出值。以NSE指标为目标函数，采用遗传算法(GA)优选LSTM的超参数。为了便于分析输入变量的相对重要性及其变化，构建单输出LSTM神经网络用于洪水预报。

1.3 GR4J-LSTM混合模型

GR4J-LSTM混合模型将GR4J模型保留一定物理特性的预报流量、前期流量及降水信息作为LSTM神经网络的输入变量。GR4J模型能够产生合理精度的水文过程线，但考虑到研究流域可能受到人为因素的影响，依靠自然降水-径流转化机制的GR4J模型可能难以捕捉实测流量的响应变化，而这种变化似乎可以被LSTM模型从时间序列的某些特征中捕获。因此，将GR4J模型与能够处理一定噪声(可能由偶然误差和人为因素等导致)的LSTM结合，有望提高基准模型的预报性能。

人工神经网络的输入一般为前期降水和流量等相关特征[16]。假设神经网络的输入由降水和流量两类特征组成，洪水预报依据时间为t，TP和TQ分别表示降水和流量的最大时滞，s表示预见期长度，则可以得出这一类混合模型的通用公式：

(1)

(2)

图1描述了在s≤TP，s≤TQ的情况下GR4J-LSTM混合模型的结构，f(·)表示某一类输入特征的集合。GR4J模型的预报流量以补充神经网络输入变量的策略耦合到LSTM神经网络中。在模拟阶段，首先将观测到的降水量和蒸发量作为GR4J模型的输入，然后将GR4J模型的模拟流量、前期流量及降水数据作为LSTM神经网络的输入，完成模型的训练和验证。在预报阶段，GR4J模型结合预报降水资料生成的预报流量和ECMWF的预报降水数据作为LSTM神经网络的输入，以测试混合模型在实际应用中的有效性。

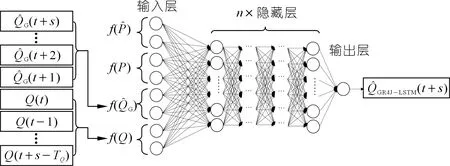
图1 GR4J-LSTM混合模型的结构Fig.1 Structure of the GR4J-LSTM hybrid model

1.4 评价指标

采用纳什效率系数(NSE)、Kling-Gupta Efficiency(KGE)系数、皮尔逊相关系数(R)和均方根误差(RMSE)4个常用指标对模型预报结果进行评价，具体计算公式见文献[20]。

R指标可以评估实测和预报流量之间的相似程度，NSE和KGE指标能够评估高流量样本对模型性能的影响，RMSE指标能够评估洪量对模型性能的影响。NSE、KGE和R值越接近于1、RMSE值越接近于0，表明预报结果和实测结果的拟合度越高。

2 应用实例

2.1 研究流域及数据资料

陆水为长江中游右岸的一级支流，陆水水库流域面积3 950 km2，属于亚热带季风气候区，年平均气温约15.5 ℃。年平均降水量为1 550 mm，年内和年际变化较大。雨季较早，一般集中在4～9月，占全年降水量的70%。平均年径流量约为33.02亿m3，最大的洪水一般发生在5～6月。陆水水库库容约为7.42亿m3，位于干流的出口处。由于库容较小和预报不确定性的限制，陆水水库在雨季面临巨大的防洪压力。因此，陆水水库需要更为准确的洪水预报，为防洪和水资源管理提供有效的决策支持。

研究资料为长江水利委员会水文局提供的陆水水库汛期(5月1日至10月31日)与洪水事件相关的数据集，包括2012～2019年17个测站的3 h降水，陆水水库入库流量和蒸发资料；2017～2019年汛期每日上午08：00的ECMWF栅格化3 h降水预报数据(空间分辨率为0.125°E×0.125°N)。

为获得水文模型输入，分别基于测站和栅格数据集插值得到流域面降水系列。研究的预见期的范围设定为3～12 h，间隔时间为3 h(定义为Dt)。在研究中，数据集被分为3部分，用于模型训练、验证和测试。训练、验证和测试期以及模拟和预报阶段的数据集如表1所列。图2表示了训练期和验证期的降雨-径流过程线。

表1 训练、验证和测试阶段以及模拟和预报阶段的数据集

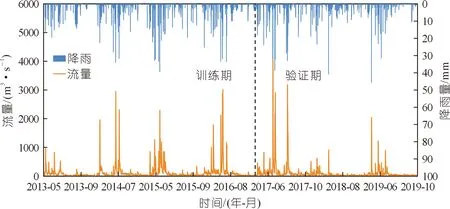
图2 训练期(2013～2016年)和验证期(2017～2019年)的降雨和径流过程线Fig.2 Rainfall and runoff hydrographs in the training (2013～2016) and validation (2017～2019) periods

此外，在测试阶段，洪水预报的起始时间为每日上午08：00(t)。因此，预见期3 h(t+Dt)、6 h(t+2Dt)、9 h(t+3Dt)和12 h(t+4Dt)的预报结果分别是2017～2019年汛期每日11：00、14：00、17：00和20：00的瞬时预报数据。

为了避免过度拟合问题，使得神经网络模型具有较好的泛化能力，表2展示了训练期、验证期和测试期流量数据集的统计特征。由表2可知，不同时期的流量数据集表现出类似的统计特征，这表明训练期的流量数据有一定的代表性[21-23]，能够训练神经网络来模拟验证期和测试期的数据。

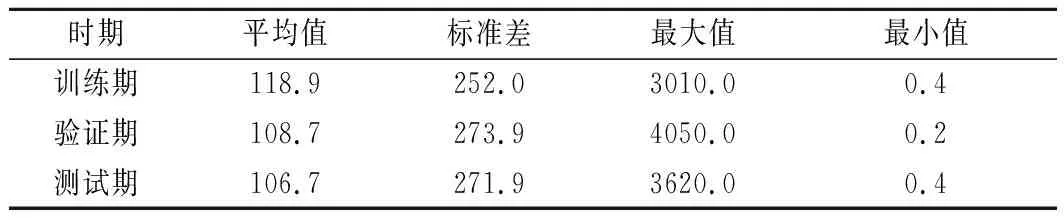
表2 训练期、验证期和测试期流量数据集的统计特征值

2.2 优选模型输入

GR4J模型的输入是降水和蒸发资料，输出是陆水水库的入库流量。LSTM神经网络的输入和GR4J-LSTM混合模型的LSTM模块相似，都是由前期降水、预报降水、前期流量和预报流量组成。期望输出为实测流量，神经网络的输入需要进一步优选。陆水流域的产汇流时间约为12 h，为了满足陆水水库运行管理的需要，降水和流量的最大时滞选为12 h。表3展示了GR4J模型和根据公式(1)和(2)得出的神经网络输入输出结构。

表3 神经网络的一个时间步的输入输出结构

3 结果分析

3.1 模拟效果分析

采用SCE-UA算法来率定GR4J模型参数。表4列出GR4J、LSTM和GR4J-LSTM模型在训练和验证阶段的洪水模拟性能。GR4J模型结构内部具有稳定的物理机制，其模拟结果的评价指标较为优良。与GR4J模型相比，LSTM模型在3 h和6 h预见期具有较高的精度，但在9 h和12 h预见期的效果较差。分析原因认为，在LSTM神经网络中，由于与输出变量相关性较高的输入变量(如前期流量特征)随着预见期的增加逐渐减少，导致捕捉输入、输出变量关系的能力变弱。如果能够持续为LSTM神经网络提供与输出变量相关性较高的输入变量，可有效缓解此类问题。由RMSE指标可以得出：GR4J模型的模拟流量具有较小的水量误差，并且R值在0.94以上，表明GR4J模型的模拟流量与实测流量具有较高的相关性。若将GR4J模型的模拟流量作为LSTM模型的输入，有望提高LSTM模型的模拟精度。

表4 GR4J、LSTM模型和GR4J-LSTM模型在训练和验证阶段的洪水模拟结果评价指标

由表4可知，GR4J-LSTM模型的NSE、R和RMSE值在不同预见期均优于基准模型(GR4J模型和LSTM模型)。GR4J-LSTM模拟流量的NSE值均在0.920以上，R值均在0.960以上，这表明GR4J-LSTM模型能够利用GR4J模型的模拟流量，在补充相关性较高的输入后，有效提高LSTM模型的模拟精度。

图3为3种模型在训练和验证阶段的实测和模拟流量散点图。与基准模型相比，混合模型的散点图更为接近1∶1线，如表4所列R值，GR4J-LSTM模型几乎一直是最优的。在9 h预见期之后，GR4J模型的R值高于LSTM模型。在验证阶段有较多高流量散点位于1∶1线以下，原因可能是参与训练阶段的高流量样本较少，所以验证阶段的高流量点被低估。

图3 3种模型在训练和验证阶段的实测和模拟流量Fig.3 Scatter plots of observed and simulated discharges by the three models in training and validation period

3.2 预报精度分析

在预报阶段，利用ECMWF的预报降水信息和地面站实测蒸发数据，驱动3种模型预报流量，以指导陆水水库的运行管理。LSTM模型的输入数据和GR4J模型的预报流量作为混合模型(即GR4J-LSTM)中LSTM模块的输入数据。洪水预报的起始时间为预报阶段每日上午08：00。因此，3，6，9 h和12 h的预报结果分别为2017～2019年汛期每日11：00、14：00、17：00和20：00的瞬时预报数据。

表5为在预报阶段3种模型洪水预报结果的评价指标。评价指标的变化规律与模拟阶段相似，但性能下降幅度大于模拟阶段，说明模拟与实际应用之间存在较大偏差。在相同的预见期下，GR4J-LSTM模型的各项指标在相同预见期下几乎均优于GR4J和LSTM模型，这表明混合模型明显改善了基准模型的多时段过程预报性能。其中，混合模型对GR4J模型的NSE指标改善较大，对LSTM模型的KGE指标和水量误差改善较大。在较长预见期下，GR4J模型的RMSE指标优于LSTM模型，具有相对较小的水量误差，这得益于模型内部稳定的降雨径流物理转化机制。

表5 在预报阶段3种模型洪水预报结果的评价指标

LSTM神经网络可以处理一定程度非线性和随机性等特点的数据。因此，经过LSTM神经网络的类似于后处理校正工作，GR4J模型的NSE指标在较高预见期内的预报流量精度得到明显改善。另一方面，由于GR4J模型的预报流量可以补充LSTM模型的输入变量，混合模型(即GR4J-LSTM)明显改善了LSTM模型的预报性能，延长了LSTM模型的预见期。这进一步突出了GR4J模型的预报流量对保持LSTM网络的预报精度具有重要意义。然而，这种程度的改善在NSE、KGE和R值方面并不是无限的，因为混合模型也会受到不同来源的不确定性的影响。例如，当输入误差随着预见期的增加而变大，混合模型的预报性能也会受到很大影响。

本次研究评估了2018年5月29日至6月3日的一场洪水事件(见图4)的预报性能。可以发现，随着预见期的增加，3个模型的洪水过程逐渐偏离实测值，说明预报性能逐渐下降。其中，LSTM模型的洪水过程线恶化最严重，GR4J模型次之，混合模型相对最优。LSTM模型低估了峰值流量，洪水过程线出现不规则波动。GR4J模型虽然由于预报降水的不确定性高估了峰值流量，但与实测洪水过程线保持相似的形状。GR4J-LSTM模型的洪水过程线同样保持了合理的形状，这说明GR4J模型的预报流量可以向混合模型传递产汇流特征，使混合模型保持合理的洪水过程线。随着预见期增加，混合模型的预报误差也加大，但它显著提高了基准模型的预报性能。

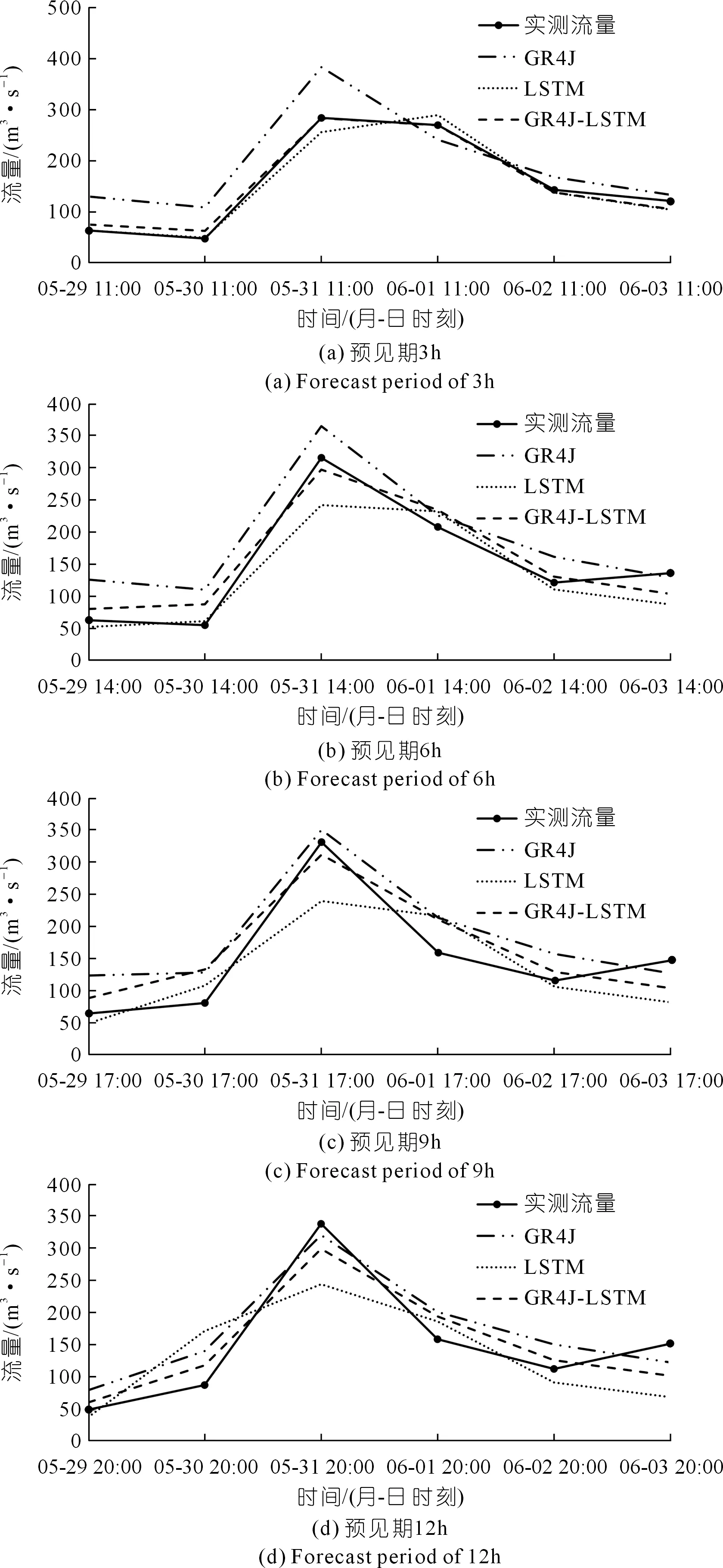
图4 3种模型在2018年5月29日至6月3日期间预报流量过程线Fig.4 Forecasted flood process lines by the three models from May 29 to June 3，2018

3.3 输入变量对模型性能的相对重要性

为了定量描述输入变量对混合模型的影响，采用了平均影响值(Mean Impact Value，MIV)算法来分析输入的相对重要性。MIV算法由Dombi等[21]提出，用来反映神经网络中权重矩阵的变化。它常用于输入变量的选择，同时它也被认为是评估输入变量对神经网络性能影响的有效技术之一。训练完成的神经网络结构是应用MIV的先决条件。MIV在训练期间对样本N的某个输入增加或减少10%，获得两个新的训练样本N1和N2；并在训练完成的网络中进行模拟，得到两个结果A1和A2，其中A1和A2的差值就是输入对输出的影响值(IV)。依次对每个输入的影响值(IV)进行算术平均计算，获得每个输入的MIV。最后，MIV的绝对值越大，对应输入变量的相对重要性就越高。为了直观地比较不同网络结构下输入变量的相对重要性，进而说明GR4J预报流量对预测精度的影响程度，本次研究对MIV的绝对值进行归一化处理。归一化后的MIV等于0或1，分别表示该输入变量在该网络结构中是相对最不重要或最重要。

图5是LSTM和GR4J-LSTM模型输入变量的MIV变化图。流量的自相关系数优于降水量与流量的相关系数，说明前期流量对模型的预报精度有较大影响。在LSTM模型中，相对重要的变量一直是时滞最小的前期流量信息。随着预见期的增加和前期实测流量数量的减少，降水量的相对重要性逐渐增加，从而导致预报精度的下降。而在混合模型中，随着预见期的增加，GR4J模拟流量的MIV逐渐增加。从预见期9 h开始，模拟流量一直处于相对最重要的位置，这对保持较长预见期的预报精度起着关键作用。考虑到预报误差是ECMWF产品的固有特性，根据MIV可以适当减少降水输入组合以降低预报结果的不确定性。通过MIV方法对神经网络结构的分析，证实GR4J的模拟流量对提高LSTM模型的预报精度有较大影响。

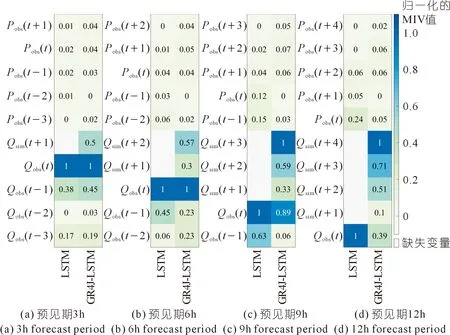
图5 LSTM和GR4J-LSTM模型输入变量的MIV变化Fig.5 Mean impact value variation of input variables for LSTM and GR4J-LSTM models

4 结 论

本文将GR4J模型的输出以补充输入变量的策略耦合到LSTM神经网络中，构成了GR4J-LSTM混合模型，在考虑ECMWF的预报降水情况下对陆水水库进行洪水过程预报，并根据MIV法进一步解释GR4J预报流量的相对重要性，得到以下结论：

(1) 降水预报的不确定性对水文预报有很大的影响，混合模型通过LSTM模块可以有效处理预报降水的噪声，改善基准模型的多时段过程预报性能。从NSE、KGE和R评价指标看，GR4J-LSTM混合模型性能明显优于GR4J和LSTM模型。

(2) 平均影响值(MIV)方法表明，GR4J的预报流量对维持混合模型较高的预报精度起着重要作用，混合模型不仅有效延长了LSTM的预见期，而且有助于维持较长预见期的预报精度。

(3) 在混合模型的框架中，LSTM神经网络可以作为后处理方法，修正GR4J模型的预报误差，而GR4J模型可以作为预处理方法，为LSTM神经网络补充产汇流过程信息，提高洪水预报精度。所提混合模型的框架可为后续概念性模型和LSTM模型结合的研究提供参考。