WSN中利用熵权自适应分簇和改进PSO的路由优化算法

杨明丽 路 翀

1(新疆交通职业技术学院运输管理学院 新疆 乌鲁木齐 831401) 2(新疆财经大学信息管理学院 新疆 乌鲁木齐 830012)

0 引 言

随着软计算的发展，无线传感器网络(WSN)在灾害预警系统、医疗保健、环境监测、安全以及监视、入侵检测、防御侦察等关键领域具有广阔的应用前景[1-2]。传感器节点包含数据聚合单元、传感单元、通信组件、能量单元。每个传感器节点可以配置全球定位系统以在给定目标区域或区域内前进。传感器网络用于从环境中收集数据并构建有关监控对象的推论。这些传感器节点通常由于功率和带宽限制而具有有限的通信能力。由于WSN的传感器节点电源一般是由电量有限的电池提供，如何高效率利用传感器能量、提高网络生命周期是路由算法研究的重点工作之一[3-4]。因此，研究无线传感器网络的能量消耗以及如何提升其使用生命周期具有很好的现实意义和实用价值。

国内外许多专家及学者围绕无线传感器的能量消耗以及如何提升其使用生命周期的问题展开了深入的研究。文献[5]基于均衡节点通信负载选择簇头，并且簇头与基站的通信使用多跳方式，以弥补单跳通信中存在能耗过大的问题。但该通信方式造成离基站近的簇头会高频率地传送离基站远的簇头信息，加剧节点死亡。文献[6]中利用非均匀分簇的方式动态调整簇半径，以缩减离基站近的簇通信半径，实现网络负载均衡。文献[7-8]基于节点的剩余能量调节下一跳的选取方位，但该方法容易出现局部最优，而无法实现网络总体低能耗的目标。文献[9]利用模糊理论与蚁群算法融合的方式构建网络路由，该算法提高了网络节点的存活率，但两个算法的权重分配具有主观性，因此结果的准确性需要进一步验证。因此，以上算法仍有一定的创新和改进空间[10]。

本文提出的模糊神经网络结合粒子群算法(FNNPSO)的WSN路由优化算法，利用模糊逻辑推理明确簇头的选择，以加强簇内架构的稳定性，并且簇间选择合适的中继节点，可增强簇间路由的健壮性与可靠性。其主要创新点为：

(1) 现有的大多数算法易陷入局部最优，无法实现网络整体低能耗，而本文算法运用模糊神经网络推理选择簇头，由熵权法确定簇头节点指标的权重，并且采用神经网络推理的评估标准获得簇头的转发概率，从而选取最优的中继节点，逐层完成信息传输，提高了网络生命周期和整体网络性能。

(2) 现有的大多数算法中，节点选取的约束条件较少且WSN的能量损耗较大，而本文算法考虑中继节点的数量、网关到基站之间的距离和网络的中继负载因子，设计了新型适应度函数，降低了网络的能量消耗，提高了簇内结构的稳定性。

(3) 现有的大多数算法中，提高了网络节点的存活率，但权重分配的主观性导致评价结果说服力不强，而本文算法利用模糊逻辑推理明确簇头的选择，且利用优化后的粒子群算法选取簇间中继节点，以增强簇间路由的健壮性与可靠性。

实验结果表明，提出的优化算法相比其他几种较新的算法，有效降低了网络的能量消耗，提高了网络生命周期，提升了网络性能。

1 算法介绍

1.1 模糊神经网络模型设计

1.1.1簇头选取

(1) 明确模糊变量。模糊变量包括节点的相对剩余能量、向心率、成功发送率和成为簇头的概率值。其中节点相对剩余能量Err是当前能量与簇内其他节点(节点总数为n)剩余能量均值的比值，该值越大，则成为簇头的可能性越大[11]。Err的计算如下：

(1)

节点向心率(Near Heart Rate，NHR)是簇头—基站的距离与簇头—簇内节点的距离之和的倒数，距离越小，NHR越大，因此该值可作为平衡能量损耗的标准。NHR的计算如下：

(2)

式中：dij是簇头与簇内节点之间的距离；dtoBS(i)是簇头与基站之间的距离。

节点成功发送率为数据成功传送至目的地的比率，计算如下：

(3)

式中：Dr是目的节点收到的信息；Tr是节点已发送信息的总量；σ是下一跳节点是否存在相邻节点的因子。

此外，节点成为簇头的概率利用模糊变量概率值获取。

(2) 构建模糊规则库。利用上述四个模糊变量构建规则库如表1所示。其节点相对剩余能量越少，向心率越小，成功发送率越小，节点成为簇头的概率就越低，反之则概率值越高[12]。

表1 模糊规则

(3) 解模糊化。根据模糊规则获得的是模糊量，但不可直接使用，因此需要一个解模糊化的过程[13]。经典的解模糊化方法有最大隶属度法、重心法、加权平均法等。由于加权平均法的运算量小且易于使用，因此本文方法的解模糊化过程采用此方法。

1.1.2熵权自适应分簇

高质量的路由中继节点能够很大程度地提高链路的性能。在进行该中继节点选取的过程中，首先利用熵权法明确簇头权重，然后结合综合评估法明确中继节点。

(2) 明确中继节点。利用模糊综合评估法选择中继节点的流程如下。

步骤1各传输层的簇头指标向量计算如下：

CHlm(ErrNHRSSR)T，其中：l=1，2，…，L；m=1，2，…，M。

步骤2根据簇头指标向量及其权重，第l层中簇头的综合评估数值理论推导为：

CVCH-lm=ωn×CHlm

(4)

式中：l=1，2，…，L；m=1，2，…，M。

步骤3各层簇头的转发概率为：

(5)

式中：PCH-lm是第m(m=1,2,…,M)个簇头在同一传输层簇头中的转发概率。

(3) 路由优化的神经网络分类。假定路由的输入层中存在2n个一样的神经元，并结合其属性获得神经元的状态usi(k)表达：

usi(k)=netsi(k)

(6)

式中：net表示神经元网络。

而针对n组不正常网络数据中呈现弱相关特征，利用模糊神经网络分类对其进行自适应训练。训练式表述为：

(7)

式中：rs表示卷积层；ys表示输出层。

经过神经网络分类算法，得到的神经元输出为：

(8)

在上述分析运算的基础上，结合神经元输出的测量偏差作相应的自适应修正，以此获得不正常网络数据挖掘的输出偏差e。其偏差表述如下：

(9)

式中：φa表示神经元a的测量偏差；φad表示神经元ad的测量偏差。

1.2 利用FNNPSO的WSN路由优化算法

在基于集群的WSN中，传感器节点被分成若干组，称为集群。每个集群都有一个簇头(Cluster Heads，CH)，其从附近的传感器节点收集数据并处理该数据，然后直接或通过其他CH发送到基站。在基于集群的WSN中，与其他传感器节点相比，CHs具有更多的工作负载。因此需要更好的方式以高效地利用其电池电量。网关可以根据网络结构和设备的可用性将数据发送到另一个网关或直接发送到基站。网关的数据处理能力与其功率成正比[14]。如果任何网关由于缺乏能量而出现故障，则会影响网络中的相关设备。如果任何中间节点发生故障，则使用此中间节点的节点必须搜索其他备用节点以发送数据，并对新识别的备用节点造成更多负载。使用网关之间的高效路由可以缓解这个问题。

PSO的灵感来源于自然界中的鱼类群体和鸟类群体活动。这些鸟类为了搜索食物或住所，经常一起活动，却没有任何碰撞。群组中的每个成员通过调整其速度和位置来跟踪组信息，由于共享群组信息，在群组中搜索食物和住所的每个鸟或成员个体减少[15]。

FNNPSO由预定义数量的粒子(Sn)组成，每个粒子为特定的问题实例提供解决方案。每个粒子将通过适应度函数进行评估。所有颗粒具有相同的尺寸。每个粒子Pi在超空间的第d维中具有位置(Pi,d)和速度(Veli,d)。因此，在任何时间点，粒子Pi都表示为：

Pi={Pi,1,Pi,2,Pi,3,…,Pi,d}

(10)

为了达到全局最佳位置，每个粒子Pi都遵循自己的最佳(Lbesti)和全局最佳(Gbest)来迭代地更新其位置和速度。使用式(10)和式(11)执行递归位置(Pi,d)和速度(Veli,d)更新。

Veli,d(t+1)=w×Veli,d(t)+a1×r1×

(Lbesti,d-Pi,d(t))+a2×

r2×Gbestd-Pi,d(t)

(11)

Pi,d(t+1)=Pi,d(t)+Veli,d(t)

(12)

式中：w是惯性权重；a1和a2是加速常数，它们是非负实数；r1和r2是均匀分布的[0,1]范围内的两个随机数。重复此更新过程，直到找到全局最佳或达到最大迭代次数。整个算法的过程如图1所示。

图1 FNNPSO算法流程

1.2.1粒子初始化

每个粒子编码为网络(包含从每个网关(gi)到基站Bs的路径)。每个粒子Pi的尺寸为D(CH或网关的数量)。用范围(0,1]中均匀分布的随机生成的数字初始化每个网关(Pi,d|||1≤i≤Sn,1≤d≤D)。第d个网关的值(即Pi,d指定一个新节点(比方说gk)到gd作为Bs的直接邻居。也就是说，gd将数据发送给gk，gk将数据发送给Bs。图2为具有12个网关和一个基站的WSN拓扑。

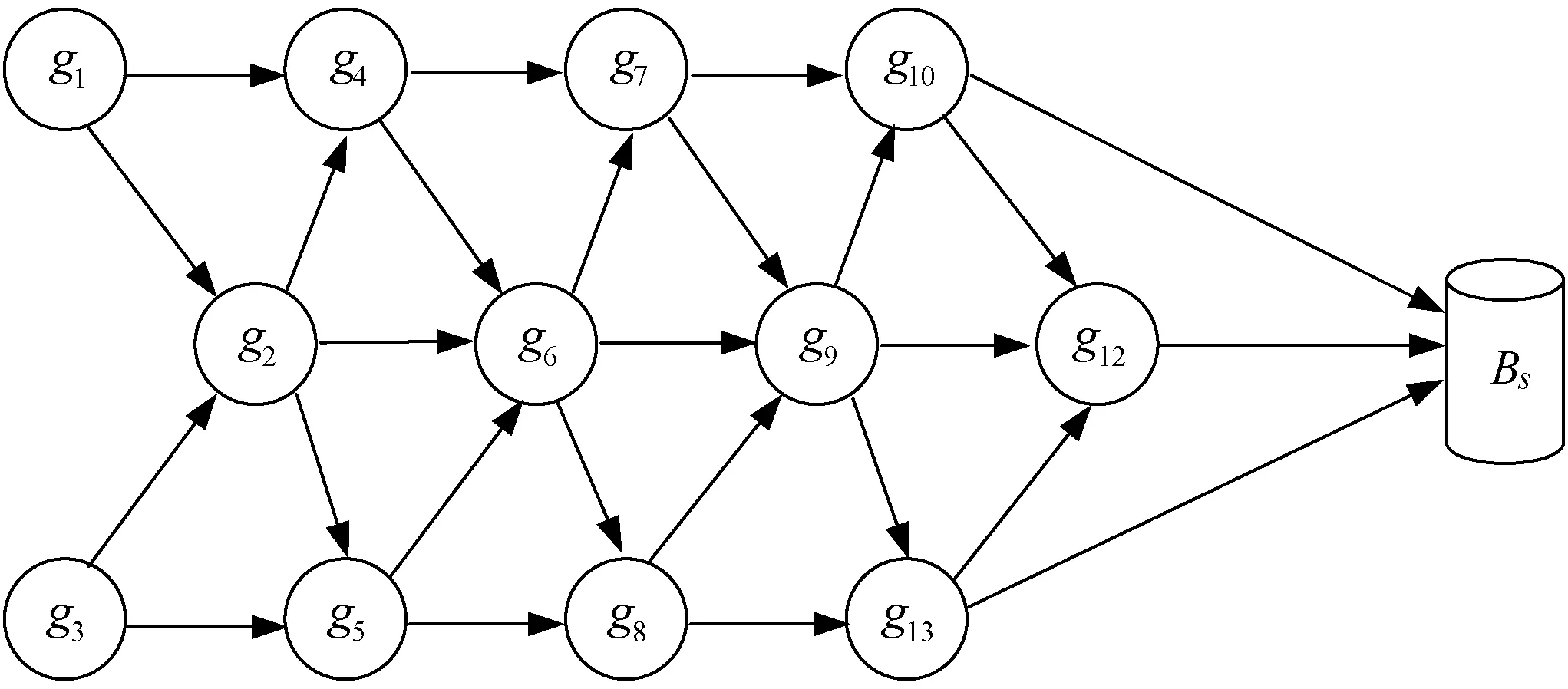
图2 具有12个网关和一个基站的WSN拓扑

1.2.2位置和速度更新

在每次迭代中，使用式(11)和式(12)更新每个粒子的位置和速度。在更新粒子的速度和位置时，由于代数加法和减法，可能会获得新的位置。新位置值可以小于或等于0，或者大于1。但是粒子位置必须在(0,1)的范围内。为了得到正确的范围值，必须在提出的算法中进行以下更改：

(1) 如果更新的位置值小于或等于零，则使用新生成的随机数修改该值，该随机数的值趋于零。

(2) 如果更新的位置值高于1，则将值修改为1。

在获得修改的位置之后，使用适应度函数来评估粒子Pi。每个粒子最佳适应值Lbesti本身都会被修改，只有当它的当前适应值优于Lbesti适应值时。在满足终止条件(迭代次数)之前，以迭代方式更新速度和位置值。在终止基于PSO的路由算法之后，最终解决方案由Gbest表示。

1.2.3适应度函数

为了评估所产生的粒子网络的良好性，提出一种新的适应度函数。拟议的适应度函数在式(13)中给出。从式(13)中可以清楚地看出，所提出的适应度函数是通过考虑三个目标而构成的。第一个目标是最小化到基站的网关之间的最大距离。第二个目标是最小化网关(网关到基站之间)用于数据传输的中继节点的数量。第三个目标是最小化网络的中继负载因子。

F=α×objective1+β×objective2+γ×objective3

objective1:minimisze{distance(gi,RelayNodes(gi))},1≤i≤N

objective2:minimisze{RelayNodeCount(gi)},1≤i≤N

objective3:minimisze{RelayLoadFactor}

(13)

式中：α、β和γ分别表示三个目标的权重，且α+β+γ=1，0<α,β,γ≤1；RelayLoadFactor=所有中继节点的总和RelayLoad值，其RelayLoad值高于AvgRelayLoad值。即:

RelayLoad(gi)≥AvgRelayLoad}

(14)

式中：RelayLoad(gi)=直接或间接通过gi发送数据的网关数。

如果网关gi不作为中继节点参与，则RelayLoad(gi)为零。AvgRelayLoad的计算如式(15)所示。

(15)

为了更好的解决方案，需要最小化适应度函数，即较低的适应度值表示最佳网络。

图3为随机粒子的表示图，中继节点为{g2,g5,g6,g8,g9,g11,g12}。{g2,g5,g6,g8,g9,g11,g12}的RelayLoad值分别为{2,31,4,3,9,11}。

图3 随机粒子的表示图

然后AvgRelayLoad=「33」/7=4且RelayLoadFactor=4+9+11=24。

请注意，在实现上述目标中的任何一个时，可能会放松对其他目标的控制。应该将所有三个目标都包括在单个适应度函数中并使其最小。为了克服目标之间的贸易问题，使用加权和方法通过考虑所有目标来制定提出的适应度函数。

2 实 验

2.1 实验准备及相关参数

基于MATLAB仿真平台，将本文算法与文献[6]、文献[8]中算法进行对比分析。其中参数设置：节点区域设为320 m×320 m，节点总数N=400，节点能量的初始值Einit=0.5 J，多路径衰减和自由空间信道模型的能量消耗分别为εmp=0.001 5 pJ/(bit·m4)和εfs=10 pJ/(bit·m2)，数据包长度L=4 000 bit，距离最大值d0=87 m，电路能量损耗Eelee=50 nJ/bit。

本文算法中，任一节点成为簇头的概率值取决于节点的相对剩余能量、向心率和成功发送率。如果三个因素中的任意一个数值较低，即使其他两个数值都较高，节点成为簇头的可能性都较小；此外，当节点相对剩余能量越多、向心率越大、成功发送率越大时，其成为簇头的可能性就越高。

使用MATLAB 2016a工具和C++语言实现本文方法。所有实验都是在两个不同的WSN场景下进行的，即WSN1和WSN2。WSN1和WSN2由50到70个网关和100到400个传感器节点组成。WSN1和WSN2仅在网络结构(拓扑)和基站放置中有所区别。WSN1和WSN2的基站位置分别为(150,200)和(300,200)。表2显示了WSN1和WSN2的常见模拟参数。为了进行比较，实现了文献[6]算法和文献[8]算法。为了验证本文方法的性能，将其与文献[6]和文献[8]所提算法在网络能量消耗、网络生命周期、总跳数和平均中继负载方面进行比较。

表2 实验模拟参数

2.2 实验结果及对比

2.2.1网络能量消耗

本文算法与文献[6]、文献[8]中方法在网络能量损耗方面的性能对比结果如图4所示。

图4 三种算法网络能耗对比

可以看出，各个算法在初始阶段的节点相对剩余能量较多，而能量损耗的差值不大，不过该值会随着网络运行轮数的上升而增加。总体上，文献[6]和文献[8]中算法的能耗量均高于本文算法，并且曲线的上升幅度也比本文算法快，由此可说明本文算法可降低网络的能量损耗。

2.2.2网络生命周期

本文算法与文献[6]、文献[8]中方法在网络生命周期方面的性能对比结果如图5所示。

图5 三种算法网络生命周期对比

可以看出，相较于文献[6]和文献[8]，本文算法中所有节点死亡时间有了一定的延长。由于算法利用模糊逻辑推理算法深层次地评价节点的性能，根据熵权法全面剖析各个因素后获得中继节点，如此可进一步平衡网络负载，进而增加节点的存活时间。

对多个传感器节点100、200、300和400执行实验。对于WSN1和WSN2两者，网络的生命周期是根据轮数(网络有多少轮数)来计算的。对于50、60和70个网关，WSN1的实验结果如图6所示。类似地，图7中展示了用于50、60和70个网关的WSN2结果。从结果可以看出，与现有技术相比，使用本文方法延长了WSN1和WSN2的生命周期。这是因为通过替代路由路径重定向来平衡特定中继节点上的负载。此过程有时可能会选择较长的路由路径作为替代方案。它增加了跳数，但整体负载分配是正确的。因此，它将增加网络生命周期。

(a) 与50个网关的生命周期比较

(a) 与50个网关的生命周期比较

2.2.3总跳数

对多个网关50、60和70执行实验，对于WSN1和WSN2两者，根据网关之间的通信计算跳数(每个网关到达基站需要多少跳数)。对于50、60和70个网关，WSN1的实验结果如图8(a)所示。类似地，图8(b)中示出了50、60和70个网关的WSN2结果。从结果可以看出，与现有文献[9]算法和PSO相比，本文方法有时需要更多的跳数。这是因为如果任意中继节点负载很重，那么本文方法选择另一个可能更长的备选路由路径。虽然本文方法有时会选择更长的路由路径，但这有助于延长网络的使用生命周期。

(a) WSN1

2.2.4平均中继负载

对多个网关50、60和70进行实验，对于WSN1和WSN2，网络上的平均中继负载被计算为网络中所有中继负载的平均值。对于50、60和70个网关，WSN1的这些实验结果在图9(a)中示出。类似地，图9(b)中显示了50、60和70个网关的WSN2结果。可以看出，与现有文献[6]算法和文献[8]算法相比，本文方法需要更少的平均继电器负载。这是由于在提出的适应度函数中考虑了中继负载因子。

(a) WSN1

3 结 语

本文提出一种WSN中利用熵权自适应分簇和改进PSO的路由算法，通过MATLAB完成仿真实验，相比其他几种较新的算法，本文算法可以有效降低网络能量消耗并且延长节点的死亡时间，进而增加了网络的生命周期。

未来主要有两个研究方向：(1) 重视路由健壮性的问题，并以路由健壮性为优化目标，通过本文算法找出网络生存期和路由健壮性的最佳适应值；(2) 考虑网络拥塞的情况，导致拥塞的主要原因是在线网络流量的增加，并且会严重影响到网络的性能，因此，考虑网络的拥塞情况也是下一步的工作重点。