线性代数课程涉农专业教学案例的设计与实践

韦丽梅

（广西大学行健文理学院，广西 南宁 530005）

0 引言

新农科概念于2017 年开始引起众多教育专家的重点关注。 在2018 年，中办和国办联合发布文件明确将“新农科”列为“四新”发展方向之一。 同年，“新农科建设协作组”在教育部高教司落地成立，“新时代农科高等教育战略研究项目”也在中国工程院顺利启动。教育部于2019 年成立了“新农科建设工作组”并发布了《安吉共识》，开启了中国高等农林教育的新纪元。

“新农科”的“新”有如下特征：（1）“新农科”专业的设置要逐步适应农业农村现代化发展需求；（2）“新农科”要服务农业农村现代化发展过程中的新产业和新业态；（3）“新农科”专业的设置要反映科学技术和新兴产业发展的最新成果。

“新农科”建设对农业学科发展和社会经济发展有深刻影响。一方面，“新农科”代表着经济社会发展、科学技术发展的农科发展方向。 建设“新农科”需要建设可适应经济社会发展和现代化发展要求的新农林高校。另一方面，通过“新农科”建设能更好地为农业农村现代化和经济社会发展提供合格的人力资源， 使人才培养、经济社会发展和农业农村现代化更好地融合。截至目前，农林高校已经具备了发展“新农科”的基础，但也存在相当多短板， 其最大的短板之一就是农林高校的理工教育和人文教育仍不够， 其发展所必需的信息技术、生物技术、工程技术、材料技术、政策研究等需要强大的数理化和人文学科的支持不够。

1 新农科背景下线性代数课程教学存在问题

广西农业职业技术大学 （以下简称 “广西农职大”）于2021 年5 月由原广西大学行健文理学院和原广西农业职业技术学院合并转设。 作为广西第一所农业类职业本科大学，在新农科背景下，如何发展一条具有区域特色的专业建设道路仍在探索之中。 线性代数作为经济管理类、理工类、农学类专业本科生的一门公共必修课，涉及的主要课程内容有：矩阵、行列式、向量组的线性相关性、线性方程组、矩阵对角化等内容。 通过多年的教学实践与学生反馈，广西农职大学生在线性代数学习过程中存在以下两大问题：（1）课程内容抽象，课程知识点前后逻辑性强，学生在学习过程中缺乏积极性和主动性，前期学习基础不扎实严重影响后续学习效果；（2）课程学时压缩与课程内容丰富的天然矛盾，导致众多知识点只能泛泛而谈，无法满足涉农专业实际的需求。 文献[2]主要介绍了线性代数在现实生活中的几个应用案例， 但是案例中没有建立与农业专业的关联。 在新农科背景下，如何将线性代数有关理论知识点涉农专业建立关联，展开具有广西农业职业技术大学特点的教学以实现产教结合，是广西农职大线性代数教学急需攻克的一个难点。 本文总结了广西农职大涉农专业的几个典型应用案例，将其融入线性代数课堂教学实践，改变学生对涉农专业不需要数学知识的错误印象，增加了课堂教学的趣味性和互动性，学生的学习兴趣热情高涨，教学效果和质量得到保证。

2 典型应用案例介绍

案例1：广西农职大与现代农业展示基地、综合性生态园八桂田园接壤，拥有规模庞大的现代农业示范园区，利于农林园艺系学生利用“专业劳动课”时间参与护理一批水果，水果涉及的品种多样，有火龙果、沙糖桔、皇帝柑、大青枣、草莓等。 已知火龙果（记为A）、沙糖桔（记为B）、皇帝柑（记为C）每斤的成本及产量分别如表1 和表2 所示。

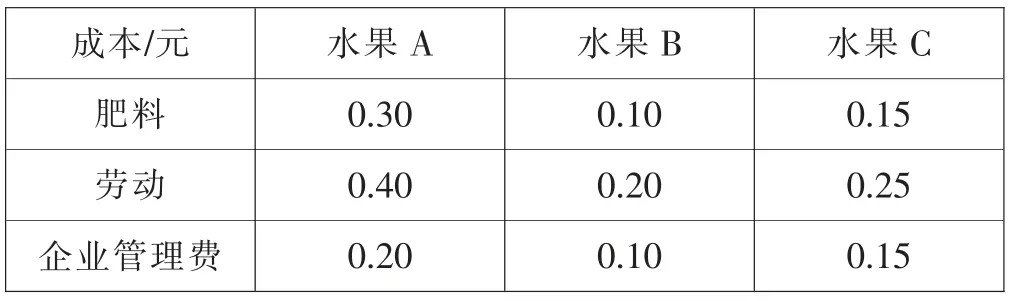
表1 每斤水果的分类成本

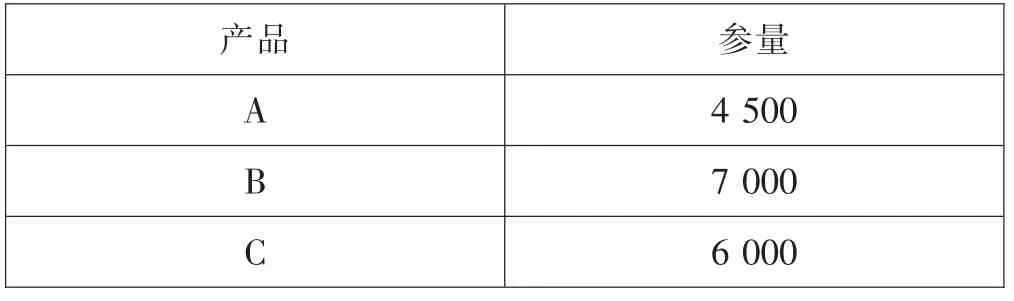
表2 产量数

要求学生核算现代农业示范园区水果种植总成本。

案例2：广西农职大动科系学生的实训课要求大鹏养殖一批60 天左右的公鸡和母鸡。 为保证鸡的存活率，大棚安装了暖气管，保证白天温度为20℃，夜间温度为22℃。 月用电量和用电费用如下表4、表5所示。

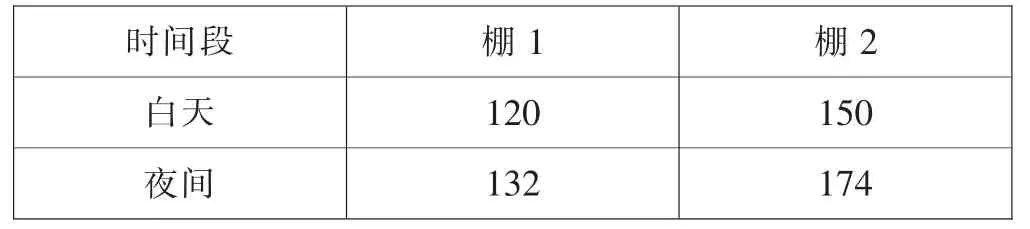
表4 月用电量

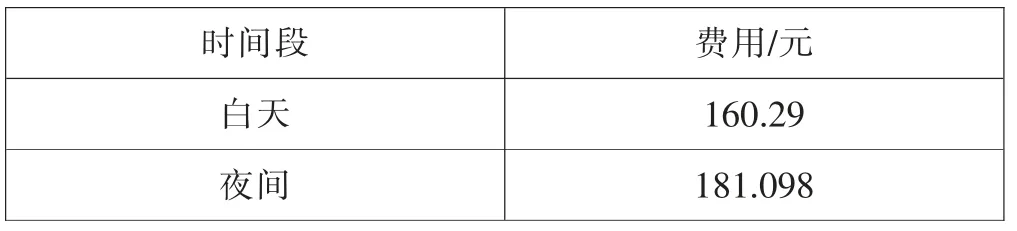
表5 用电费用

要求学生计算并比较白天和夜间的暖气管费用。

案例3：栽培技术是广西农职大的优势专业之一。比如大棚种植草莓，根据专家的建议，当温度在20℃～25℃时有利于草莓的生长。 为了控制棚内的温度，棚内安装有薄金属板。 根据实践测得该平板的周边温度如图1 所示。

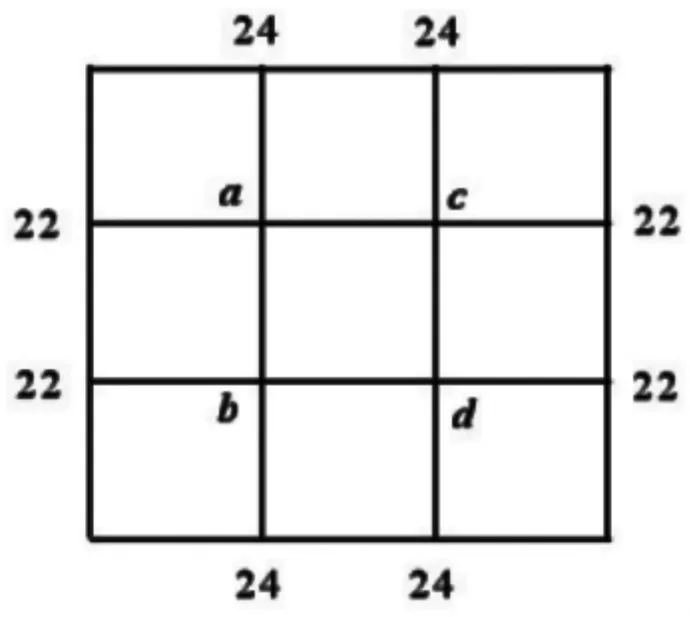
图1 大棚金属板上温度分布示意图

要求学生计算铁板中间4 个点a，b，c，d 处的温度，使其达到种植草莓的适宜温度。

案例4：畜牧兽医是广西农职大的另一优势专业。动科系学生利用“专业劳动课”时间，自己购买原料和青鱼苗，按照某青鱼饲料配方自己配制饲料。 根据兽医推荐，青鱼食谱中蛋白质、脂肪和碳水化合物三种物质的黄金比例应为40%、6.5%和30%， 目前仅备有干草（记为A）、菜籽粉（记为B）、大麦（记为C）、蚕蛹（记为D）4 种原料，且知道4 种原料所含蛋白质、脂肪和碳水化合物情况如表6 所示。 要求学生合理配制原料得到满足要求的青鱼饲料。

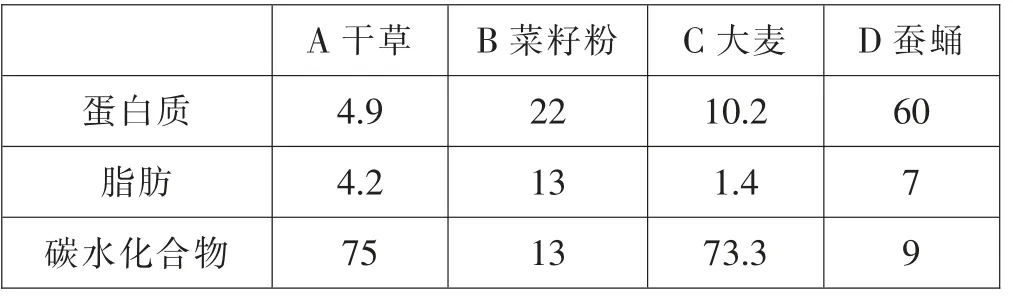
表6 饲料配方表

3 典型应用案例与线性代数教学

广西农职大涉农专业具有区域特色，考虑在线性代数课程教学环节融入农学相关案例，旨在激发学生的专业自信心，活跃课程的氛围，增加课堂的趣味性和实用性，提升课堂教学质量。

3.1 应用案例1 与矩阵乘法运算

矩阵乘法是矩阵运算的重要内容。 设矩阵A 和B维数分别为m×p 和p×n，记矩阵C 为矩阵A 与B 的乘积，可知其维数为m×n，且矩阵C 中第m 行第n 列元素等于矩阵A 第m 行元素与矩阵B 第n 列元素的乘积之和。学生普遍反映该运算规则较为抽象，对其可应用性存在疑惑。在矩阵乘法运算教学环节，引入应用案例1。 将水果分类成本记为矩阵M，季度产量记为矩阵P，根据矩阵的乘法运算，总成本矩阵为Q=MP。 借助Matlab 软件的强大运算功能便可计算出相应结果为Q=[2950；4700；2500]。 根据以上计算结果可得现代农业示范园区水果种植总成本，见表7。 由表7 可知，肥料、劳动力、企业管理费的总支出为10 150 元。

表7 现代农业示范园区水果种植总成本

当设置出售的价格低于市场价，比如火龙果定价5 元，沙糖桔定价3 元，皇帝柑定价4 元，根据收益等于价格乘以产量可计算总收益为67 500 元，那么利润为57 350 元。 在此基础上开展进园采摘活动，稍微提高价格，即可大大增加学校的额外效益。

3.2 应用案例2 与矩阵逆运算

矩阵逆运算是矩阵运算的重难点知识点。设A 是n 阶满秩方阵，若存在n 阶矩B，满足关系式AB=BA=I，其中I 为单位矩阵，那么称A 和B 互为逆矩阵。 学生普遍反映该运算规则较为抽象，对其可应用性存在疑惑。 在矩阵逆运算教学环节，引入应用案例2。 用矩阵Q 表示白天和夜间的电费标准， 矩阵M 和P 分别表示两个饲养棚一个月的用电量和用电费用。 根据矩阵的乘法运算可得月花费的电费为矩阵P=MQ， 从中解出Q=MP。借助Matlab 的矩阵求逆命令inv 有计算结果Q=（0.672，0.531）， 即白天的电费为每度0.672元，夜间的电费为每度0.531 元。 通过结果可知，夜间使用暖气管比较省钱。

3.3 应用案例3、4 与线性方程组

线性方程组在工程、物理和生物等领域均有广泛应用，如线性规划问题的求解可转化为带约束条件的线性方程组问题。 常见的线性方程组求解方法包括克莱姆法则和矩阵消元法。 学生普遍对上述方法的原理掌握不到位。

在线性方程组教学环节，引入应用案例3 和案例4。 在案例3 中， 记a，b，c，d 4 个点的温度分别为xa，xb，xc，xd，容易导出如下方程组：

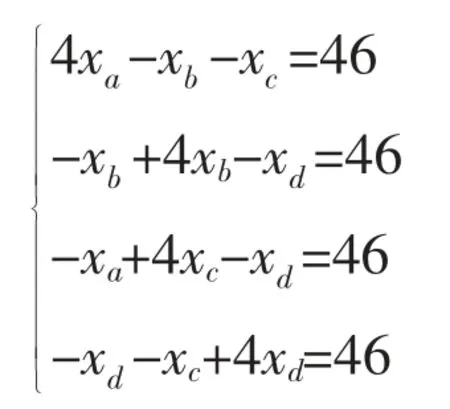
对于三阶以上方程组的求解，学生普遍反映存在计算障碍。 在课堂讲授环节，借助Matlab 软件inv 命令可得运行结果得x=[23；23；23；23]， 即四个点的温度均维持在23℃，因此是适宜草莓生长的。

在案例4 中， 记生产1 个单位的饲料所需要的A、B、C、D 4 种原料的数量分别为x，x，x，x， 构建如下线性方程组：

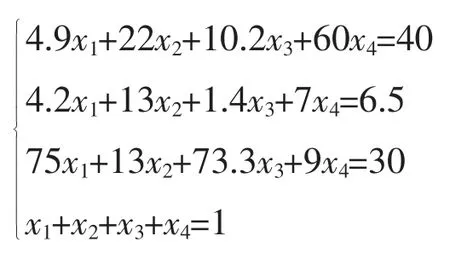
类似地， 借助inv 命令有计算结果为x=[0.2921；0.0737；0.0222；0.6120]，可知干草、菜籽粉、大麦和蚕蛹的用量分别为0.292 1g、0.073 7g、0.022 2g 和0.612 0g，按此配方就可以保证一条青鱼每日所需的营养量。

4 结语

总结新农科背景下广西农职大线性代数课程教学存在的普遍问题， 介绍了广西农职大涉农特色专业的几个典型应用案例， 探讨了应用案例与线性代数课程重要知识点——矩阵运算和线性方程组的内在联系，增加了课堂的趣味性，有效地提高了课堂教学质量。