FEM-DEM耦合弹塑性土体插桩过程力学特性研究

王浩然,张少坤,徐 文

(北京市勘察设计研究院有限公司,北京 100038)

近年来,为满足大规模基坑群插桩工程的需要,越来越多的数值计算手段被用于插桩工程的分析中。插桩技术数值模拟方法在许多工程应用中非常重要,并广泛应用于桥梁与海岸工程以及深部岩土工程的建设当中。随着大型岩土工程建设的开展,小直径钢管桩难以满足大型工程需求,因此大直径钢管桩逐渐被运用于桥梁工程、海岸工程、岩土工程中[1-3]。

许多学者针对大直径钢管桩的承载特性的数值模拟、施工方案等开展了深入的研究工作。张明远等[4]开展了基于ICA-SVM(independent component analysis and support vector machine)的超长大直径钢管桩承载力预测研究工作,确定了ICA-SVM模型的预测结果可用于超长大直径钢管桩承载力的设计。张海洋等[5]对大直径钢管桩水平载荷进行了试验研究,针对上海地区某高桩墩台工程承载力无法满足设计要求的问题,采用优化桩尖结构设计提高桩基承载力。学者们对大直径钢管插桩过程中的力学分析主要集中在试验方法和数值预测上,而对于插桩过程中土体或深部岩土性质以及岩土颗粒之间运动和相互作用力、插桩过程中复合钢管与土体间的作用力变化的研究相对较少。Haddad等[6]及Michael等[7]采用数值模拟的方法进行了离散元与有限元耦合计算在固体受力方面的研究。

受以上文献的启发,研究结合某大桥插桩项目,建立了一个模拟一次插桩深度下钢管与砂土层插入模型,利用有限元与离散元(FEM-DEM)耦合方法对大直径钢管桩的插桩过程进行数值模拟,并对其力学特性进行分析,以保证插桩过程符合工程要求。

1 数值方法与控制方程

FEM-DEM耦合方法的控制方程是通过计算颗粒与结构之间的受力来更新运动情况。DEM中计算出的插桩钢管运动时颗粒对钢管的作用力情况如图1所示。

图1 插桩过程中桩体受力示意图Fig.1 Stress diagram of pile body during pile insertion

1.1 颗粒运动方程理论

在DEM的框架内,一大组耦合的常微分方程应该随着时间的推移被求解,以获得颗粒的动态行为。方程描述了一个球形颗粒的平移和旋转运动(在三维空间有6个自由度的运动)。

(1)

(2)

其中:n是与粒子i相互作用的相邻粒子的接触数。

通过积分牛顿第二定律能够描述离散颗粒的平移情况,即

(3)

其次，建设主题鲜明、富有特色的场馆和多媒体平台。比如：建设闽东红色文化展陈馆、畲族文化主题展馆、廉政文化馆等，既可展示特色文化和资源，也可为实践教学和主题学习活动提供场所；结合闽东特色文化，建设学术报告厅、音乐厅、学生活动中心等，举办以闽东特色文化为主题的报告会、诗歌朗诵、演讲比赛、音乐会，陶冶学生的情操；成立闽东特色文化研究中心，建设闽东特色文化专题网站，开通“闽东之光”微信公众号，全面推进闽东特色文化入脑、入心。

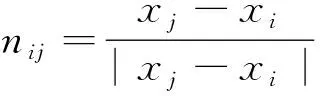
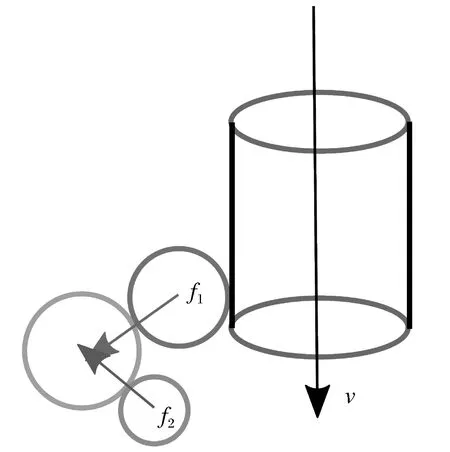
图2 颗粒之间作用力的传递分析Fig.2 Transfer analysis of force between particles

颗粒的转动依靠扭矩和滚动摩擦。滚动摩擦力是施加在固体颗粒表面上的,摩擦力可以产生一个相对于固体中心点的扭矩。固体上的总扭矩是所有组成颗粒扭矩之和。颗粒相对运动摩擦示意图如图3所示。

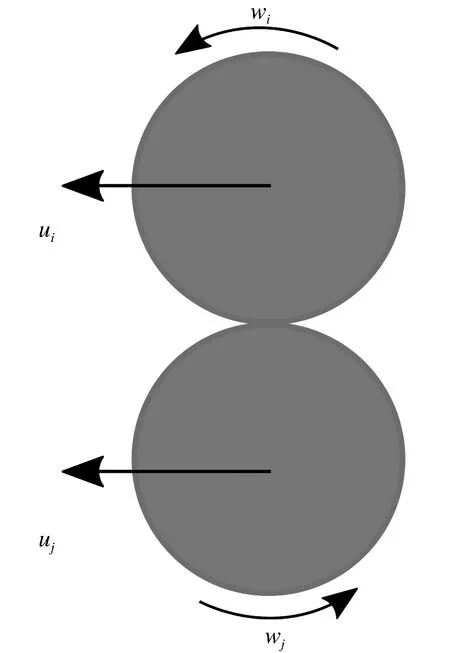
图3 颗粒相对运动摩擦示意图Fig.3 Schematic diagram of relative motion andfriction of particles

具体可通过滑移与旋转公式进一步了解,即

ui-wj×r≠uj+wj×r,

接触点的相对滑动矩Tt=μFN·r,wi≠wj,相对旋转矩Tr=μrollingFN,其中:u表示颗粒的速度;w表示颗粒的角速度;μ表示颗粒的摩擦系数;FN表示正压力。

整个球体颗粒的扭矩是所有接触颗粒作用的扭矩之和。在运动过程中无论颗粒之间是平动还是转动都会对移动钢管产生作用力。

1.2 FEM控制理论

在有限元方法中,把计算域离散剖分为有限互不重叠且相互连接的单元,在每个单元内选择基函数,用单元基函数的线性组合来逼近单元中的真解,整个计算域上总体的基函数可以看作由每个单元基函数组成,通过基函数将颗粒的力传递到固体网格单元上,求解整个计算域,结果可以看作是由所有单元上的近似解构成。

2 离散元与有限元模型参数设置

2.1 土壤颗粒模型的建立

模拟所建立的土壤模型为球形颗粒。由于土壤颗粒的粒径越小,模拟计算的时间越长,为了提高计算速度采用粗颗粒方法。粗颗粒方法被认为是颗粒计算量大的简化方法[8-11],把模型设置为由5～10 mm的球形颗粒所组成的土体模型,总颗粒数为100 000,砂壤土颗粒的泊松比为0.3,砂壤土颗粒密度为2 500 kg/m3,土壤剪切模量为1×106Pa,砂壤土之间的恢复系数为0.6[12],在DEM通过bond键设置颗粒之间的粘结强度能够实现颗粒之间的胶结,实现土体受到挤压之后破裂分散的效果。

为了能够更好地体现插桩过程中土体对桩体的应力-应变关系,将土壤接触模型设置为弹塑性粘接(EEPA,edinburgh elastic-plastic adhesion)模型,其参数主要包括了细观接触表面能Δγ、初始接触力f0、接触塑形比λp、粘附分支曲线幂指数x、非线性曲线幂指数n和切向刚度因子ζtm。由文献[13-14]可知Δγ=50,f0=0,λp=0.7,x=5,n=1.5,ζtm=0.285 71。土壤颗粒模型构建和接触模型的选取按照DEM软件中现有的接触和材料模型,建立了长1 000 mm、宽1 000 mm、高300 mm的土层,如图4所示。需要保证土体长度大于插桩管径的2倍以上,这样有助于消除边界影响。

图4 离散元法建立土体模型Fig.4 Establishment of soil model by discreteelement method

2.2 钢管桩模型建立

在三维建模软件中建立简化的钢管桩模型,如图5所示。图5中内径为0.36 m,外径为0.50 m,壁厚为0.07 m,高为2 m,屈服强度为235 MPa,密度为7 850 kg/m3,弹性模量为200 MPa,泊松比为0.30。在模拟过程中设定钢管桩以1 cm/s向下的速度插入土壤,保证每次施工桩管贯入深度为0.5～1.0 cm的工程要求。

图5 插桩钢管模型Fig 5 Steel pipe model for pole insertion

2.3 网格划分

在数值模拟中对网格进行划分是一项至关重要的工作,其直接影响计算的效率以及精准度。根据模型各部件的特性,将计算域划分为六面体结构化和非结构化网格并进行分块。为了能够获得更加精确的数值解,对钢管底部网格进行了细化,划分如图6所示。

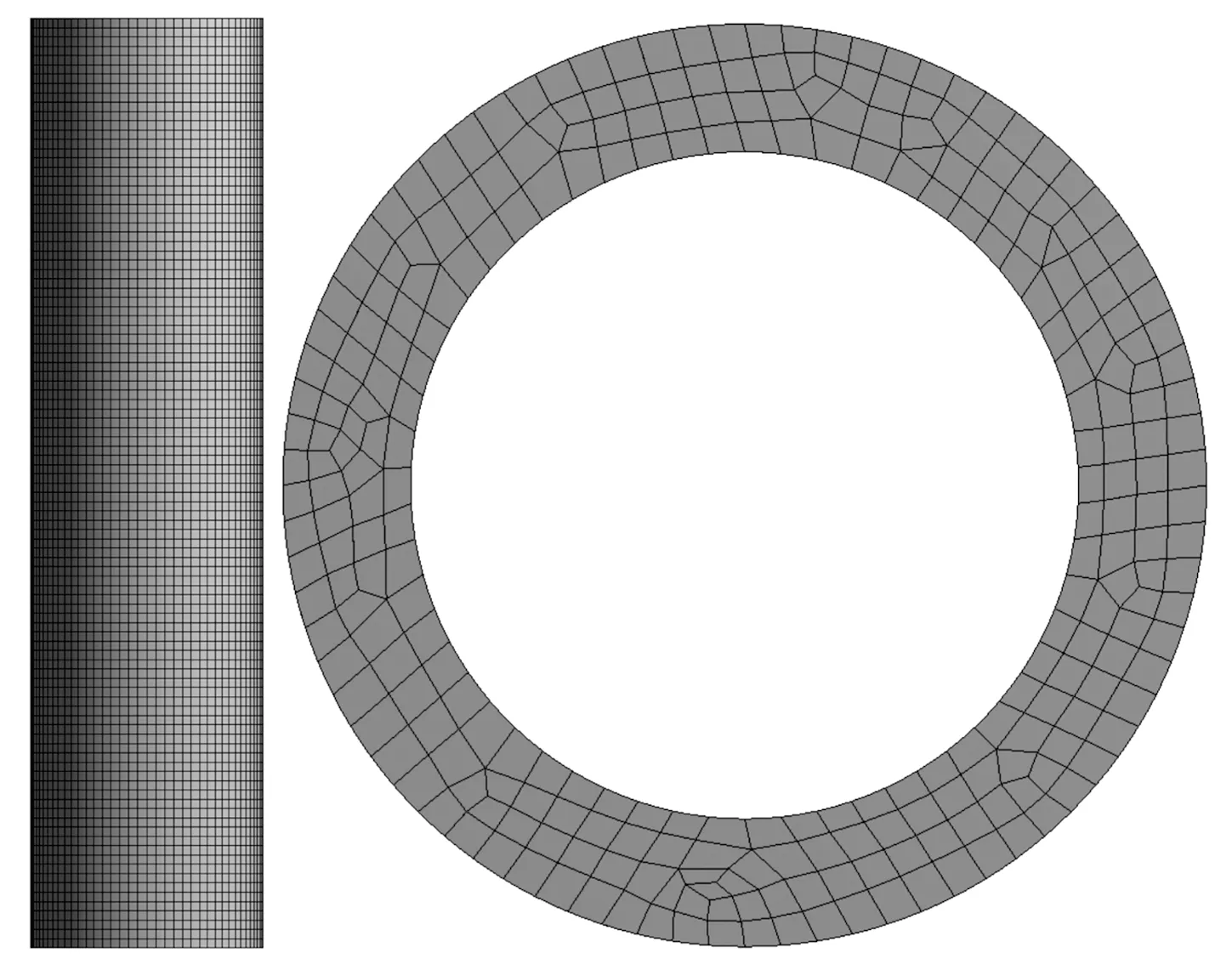
图6 桩管的网格划分Fig.6 Grid division of pile pipe

3 数值模拟结果与分析

首先采用离散元数值模拟方法,目前该方法被成功应用于多种结构体与离散的介质之间的相互耦合,这使DEM与有限元模拟大直径钢管桩受力特性计算结果的可靠性与准确度得以保证[13-14]。通过DEM-FEM耦合方法对砂土地质条件下大直径钢管桩竖向承载特性进行深入研究,能够揭示竖向荷载作用下大直径钢管桩插入土壤不同深度时受力特性的变化规律以及软质土体颗粒的运动特性。

3.1 颗粒运动特性

在整个插桩过程中桩体对土体的作用力使得土体发生变形并且导致土体颗粒之间移动。土体模型在插入过程中的动力学状态如图7所示。

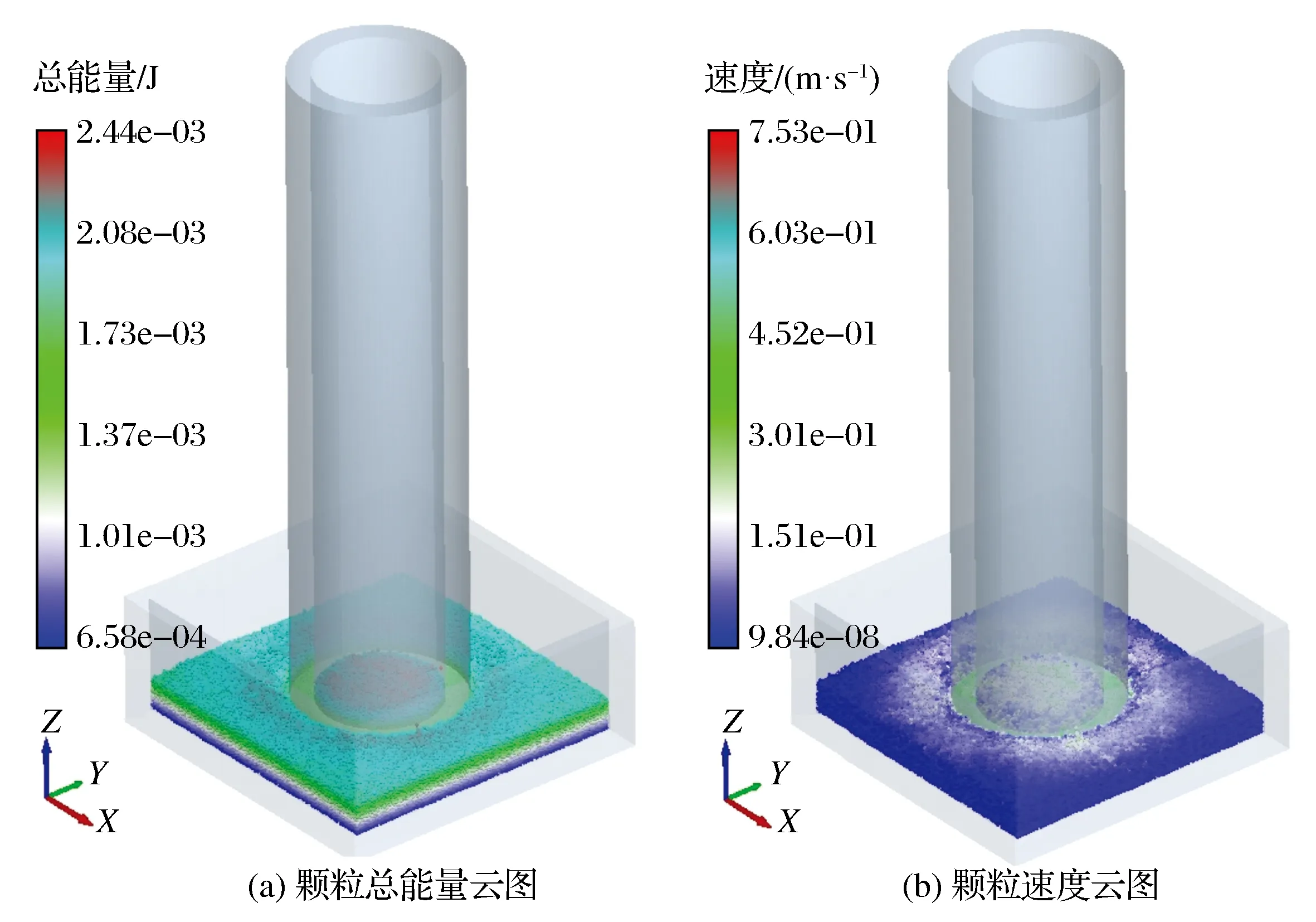
图7 桩体插入土体后的颗粒能量云图及颗粒速度云图Fig.7 Soil energy and velocity cloud after pile insertion into soil

通过颗粒的能量云图及速度云图了解到,桩管插入土体过程中桩管周围土体颗粒的能量和速度均增大,这在土体颗粒的运动特性曲线中得到进一步验证,变化情况如图8所示。

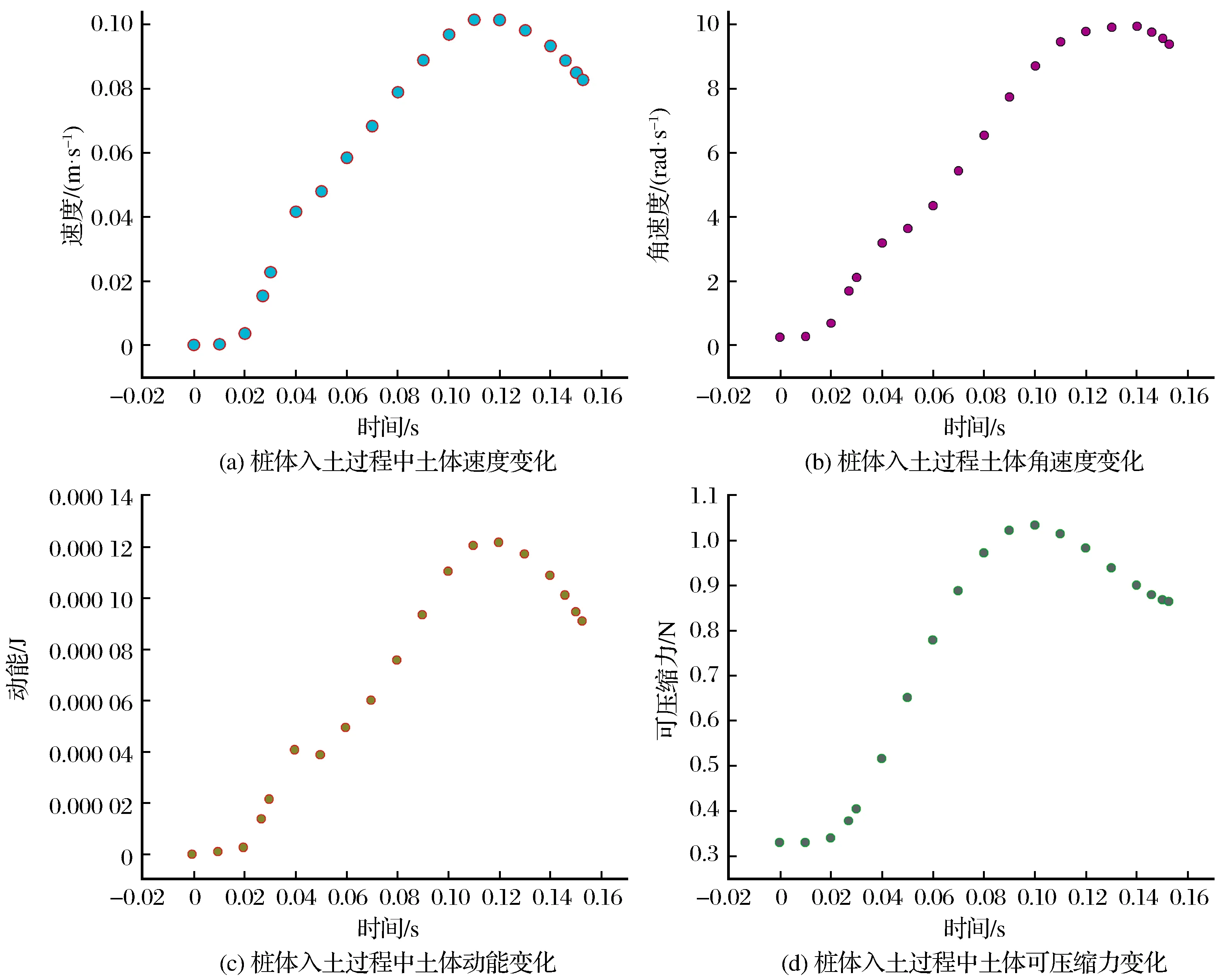
图8 插桩过程中土体的动力特性变化Fig.8 Characteristic changes in the dynamic properties of the soil during pile insertion

图8表明了桩管对土体的作用力使得土体颗粒发生运动,随着插入时间以及深度的增加,土体承受压力使整体运动速度增大,当土体达到破坏极限时颗粒运动速度减慢。

3.2 钢管底部力学特性

由于土壤颗粒之间存在孔隙使得其具有一定的可压性,参考图8(d)中的压缩力变化,通过作用力与反作用力关系可知,随着时间的延长,在0～0.15 s插桩所受到的力呈现先增大后减小的变化。0.1 s时土体作用在管道上的压力情况如图9所示。

图9 0.1 s插桩桩管所受到的土体压力Fig.9 Pressure of soil on 0.1 s inserted pile tube

从图9中可以看出,钢管桩所受到的应力并不均匀,由于钢管桩下部与土壤直接接触,其所受应力主要集中在下部。但是底部并不是每一个部位都受到很大的应力,由于土壤颗粒的粒径不均匀,而且不同的位置压实程度也不相同,与颗粒直接接触的部分不同会使得插桩受力不均匀,从而导致桩体的每个位置的应力都不相同。钢管桩继续插入时,由于土壤的压实程度较高,颗粒与管桩之间发生相对转动使得在0.1 s时土体开始破裂,从而导致管道整体的受力减小。这一过程即可表征每一次的插桩情况。

采用有限元方法对峰值压力下的应力-应变以及位移情况作进一步分析,如图10所示。

桩管在插入过程中接触面应力分布(最大值为1.2 MPa)不均匀,使得桩体在插桩过程中管道发生一定的位移(见图10(a)),从而偏离设定的插桩位置(见图10(b)),可能导致插桩的失败,因此需要详细了解整个过程中桩体偏移的初始位置情况。图10(c)显示了钢管桩在插桩过程中峰值时刻下沿Y轴方向的位移情况。由于钢管桩在水平位移作用下出现横向弯曲变形,因此基桩弯曲峰值点是桩-土界面分离的终点,也是桩基变形性能及承载力分析的重要指标。图10(c)中的管道弯曲仅存在于表层插入的情况下,如果插入深度更大,会导致插桩管损坏。

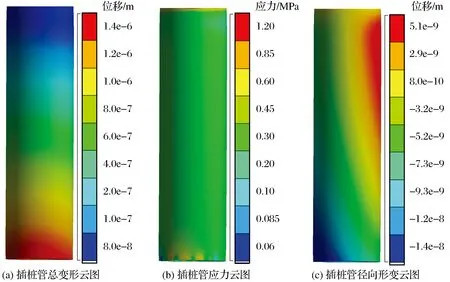
图10 插桩过程中峰值作用力下插桩管动力学响应情况Fig.10 Dynamical response of the inserted pile tube under the peak force

变形量沿管道位置的变化如图11所示,通过图11能够进一步了解整个管道的径向变化情况。

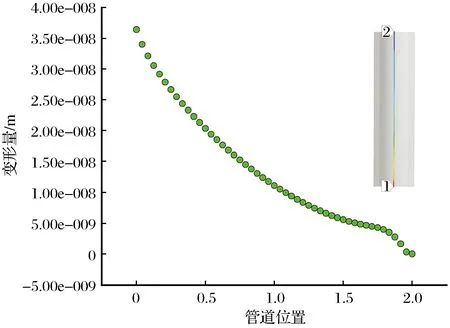
图11 变形量沿管道位置的变化Fig.11 Variation of deformation along pipeline position

由于偏移的持续存在导致整个插桩过程的桩体倾斜,进而导致插桩完成之后桩体与垂直方向存在夹角,这种存在角度的桩体使得整个结构在受力过程中不稳定,当工程中采用这种桩体时极易导致桩体的耐用性降低,引起工程事故,降低工程寿命。因此在插桩过程要注意随时修正插桩的角度并测量插桩偏移量,同时尽可能平整插桩土体表面。

4 结论

研究采用FEM-DEM耦合的方法,建立了土壤模型,并以大直径钢管桩为研究对象进行了插桩模拟,探究其在插入土体过程中的管道应力、位移等受力特性与土体运动规律,得出以下结论:

(1) 大直径钢管桩底部与土体的接触面所受总应力最大值为1.2 MPa,应力随钢管桩插入土体导致土体破裂而减小,由此可知管道所受到的作用力与土体的物性参数有直接关系。

(2) 通过应力和变形云图可以看到在桩底部处的应力处于最大峰值1.2 MPa,是应力最小处(0.06 MPa)的20倍,最大变形量(1.4×10-6m)约是最小变形量(8×10-8m)的175倍。所以在设计钢管桩时,可增大其底部的承载能力,使插桩过程更加稳定。

(3) 在插桩过程中,大直径钢管桩沿径向方向发生不均匀弯曲,径向变形从最大值3.75×10-8变化至0后甚至出现反向的变形。这种弯曲或者变形非常容易导致插桩方向发生变化,使得插桩结果出现较大的误差。