考虑行波效应的大跨度双塔斜拉桥地震响应分析

曾玉华

(湘潭市交通建设质量安全监督站， 湖南 湘潭 411100)

地震波速度的变化、场地差异等极大影响大跨度斜拉桥的地震响应。地震波传播时达到不同站点的时间差异(即行波效应)会使各站点的地震响应明显不同。喻明秋等利用有限元软件MIDAS/Civil分析了不同波速下支承体系斜拉桥的地震响应，结果显示行波效应对结构位移和内力峰值影响较明显，且其响应峰值具有明显的周期性；方圆等采用时程分析法研究了行波效应对大跨度多塔斜拉桥的影响，结果显示，塔、梁间约束不同，行波效应对其影响存在差异，塔、梁间固定时影响较大，活动时影响较小；卜一之等研究了行波效应对六塔斜拉桥的影响，认为考虑行波效应时结构的内力响应和位移响应均小于一致激励下的响应，其中对边跨附近桥塔和主梁跨中内力、位移响应的影响最明显；王再荣、许智强等的研究结果表明，行波效应对斜拉桥的影响既有利也有不利，并不单一。综上，大多数研究针对行波效应对斜拉桥整体结构的响应，很少分析行波效应对斜拉桥拉索索力的影响。该文以某大跨度双塔斜拉桥为例，利用MIDAS/Civil建立有限元模型，采用相对位移法分析地震作用下行波效应对斜拉桥拉索索力、典型截面内力和位移的影响。

1 基本理论

1.1 基本方程

假设桥梁结构的外部荷载为F(t)，根据达朗贝尔原理，该结构的运动微分方程可表示为：

(1)

以g表示与桥梁支座处有关的项，s表示与桥梁非支座处有关的项，当桥梁结构的地震响应考虑多点地震动输入时，其运动微分方程可由分块矩阵表示：

(2)

1.2 相对位移法

相对位移法的运动方程为：

(3)

仅计算拟静力位移时，其位移关于时间的导数均为零，根据式(2)，得：

(4)

将式(4)展开，化简变形后得：

(5)

(6)

式中：[D]为拟静力矩阵。

将式(3)、式(5)代入式(2)，由于阻尼力比其他力小，忽略阻尼力，化简整理后得：

(7)

2 工程概况及动力分析模型

某对称的双塔斜拉桥，梁、塔、墩均为固结的刚构体系。主跨采用(50+95+350+95+50) m双塔双索面斜拉桥，桥面宽28 m，塔高125.8 m。桥塔两侧各设28根拉索，全桥共112根斜拉索。主梁和桥塔均采用钢筋砼结构，砼强度等级为C50，主梁采用砼箱梁结构。斜拉索呈扇形布置，拉索的编号从左到右依次为1、2、…、14(见图1)。

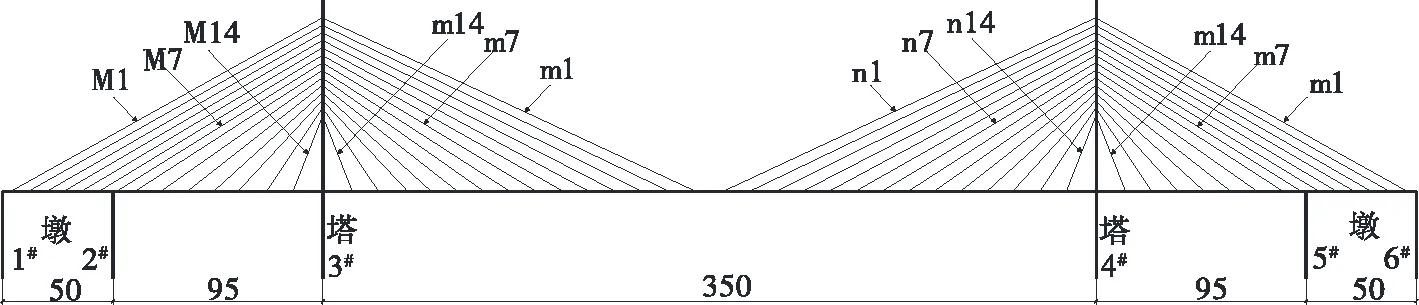
图1 某大跨度双塔斜拉桥示意图(单位：m)

利用MIDAS/Civil建立该桥有限元模型(见图2)，桩基础采用梁单元模拟，桩周土抗力的影响采用土弹簧单元模拟，桩基底部设为固结。

图2 某大跨度双塔斜拉桥有限元模型

3 动力特性分析

斜拉桥的动力特性是进行抗震分析的基础。表1为该桥前8阶自振周期和频率。从表1可看出：该桥的自振周期较长，一阶振动为主梁对称横弯，自振周期达4.621 9 s，自振频率为0.216 4 Hz，体现了斜拉桥的柔性结构特点；该桥自振频率非常密集，2阶模态之后，频率增加极其缓慢，体现了其动力特性的复杂性。

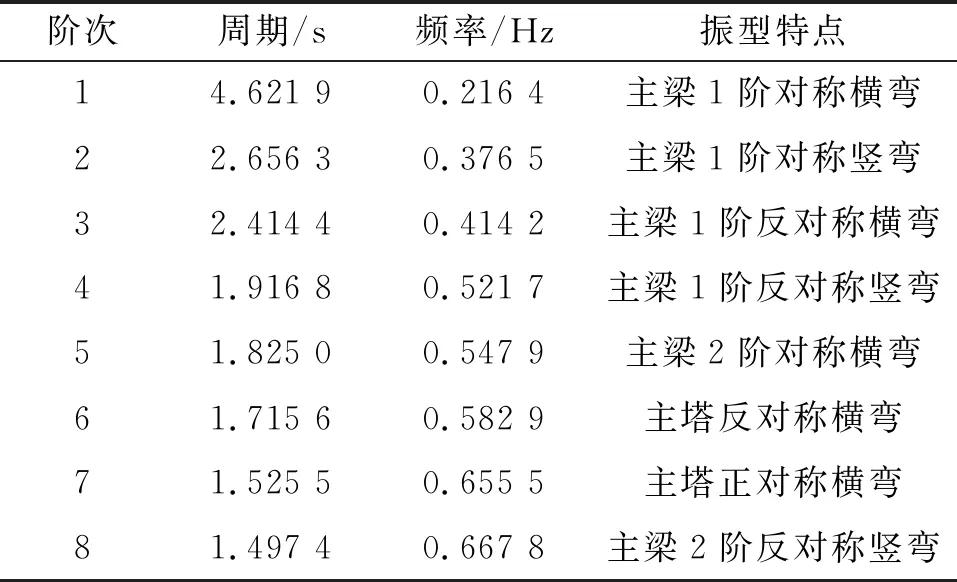
表1 某大跨度双塔斜拉桥的动力特性

4 地震波输入

地震地面运动特征中，地震动强度、频谱特性和强震持续时间对结构破坏有影响。选取结构抗震设计中具有代表性的El-Centro波(见图3)，波速分别为500 m/s、1 000 m/s、2 000 m/s、3 000 m/s和∞(地震响应中的一致激励)，分析地震作用下行波效应对该桥典型截面位移响应和内力响应的影响。

图3 EI-Centro波

5 计算结果分析

输入El-Centro地震波，对结构进行时程地震响应分析，得到不同波速下桥梁地震响应，重点关注拉索索力、关键截面(墩底和塔底)内力和典型截面(主梁)位移的变化，并与一致激励下地震响应进行对比分析。

5.1 行波效应对斜拉桥索力的影响

在主塔两侧各选取3根典型拉索，分别为远离主塔的拉索、中间拉索和靠近主塔的拉索(其位置及编号见图1)，分析行波效应对斜拉桥拉索索力的影响。不同波速下斜拉桥典型拉索在一致激励和非一致激励下的地震响应峰值见图4。

图4 索力的地震响应峰值

从图4可看出：考虑行波效应，地震波速度为500 m/s时，该桥索力响应峰值大于一致激励下索力峰值，但随着波速的增大，行波效应对索力的影响减弱，并最终趋于一致激励下地震响应结果；随着拉索长度的减小，索力逐渐减小，考虑行波效应时，不同位置处拉索索力变化无明显规律。

5.2 行波效应对墩/塔底内力的影响

不同地震波速度下墩/塔底内力响应最大值与一致激励下内力响应对比见图5、图6。

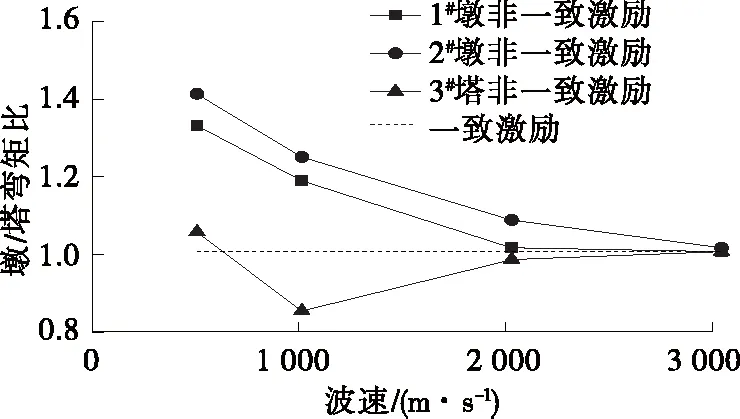
图5 墩/塔底截面弯矩比

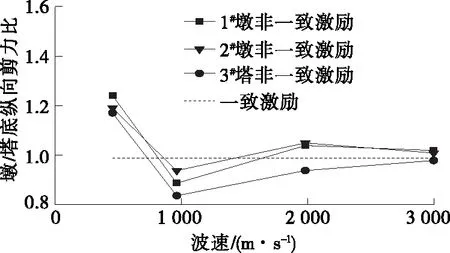
图6 墩/塔底截面纵向剪力比

由图5、图6可知：随着地震波速度的增大，各墩/塔底的内力变化趋势并不相同，有些部位的响应总体递减，而有些部位的响应有增有减。1) 随着波速的增大，1#、2#墩的弯矩呈递减趋势，最终逼近一致激励下弯矩值。波速为500 m/s时，3#塔的弯矩较一致激励时增大13%；波速为1 000 m/s时，其弯矩是一致激励下的85%，最终塔底弯矩趋近于一致激励下弯矩值。2) 波速为500 m/s时，各墩/塔底的剪力均增大，其中1#墩增幅最大，达28%；波速为1 000～3 000 m/s时，其对剪力的影响较小，最终剪力值逼近一致激励下剪力值。

5.3 行波效应对主梁和塔顶位移的影响

选取主梁跨中和塔顶，分析行波效应对斜拉桥位移的影响。不同地震波速度下关键截面的位移响应峰值见表2，与一致激励下位移响应峰值的比值见图7。

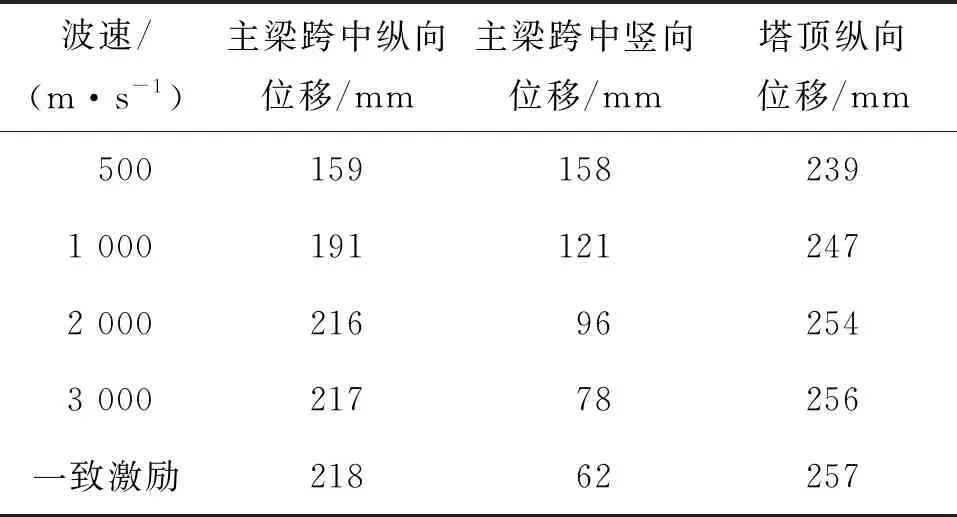
表2 不同波速下关键截面位移响应峰值

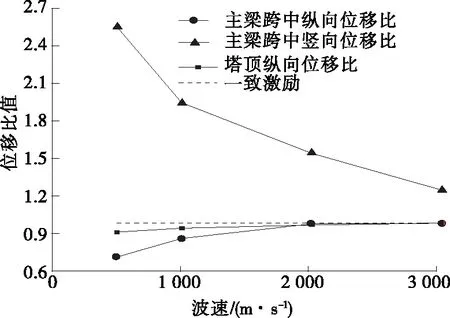
图7 不同截面非一致激励与一致激励下位移 响应峰值比值

由图7可知：考虑行波效应，主梁跨中和塔顶纵向位移较一致激励下位移都有一定程度减小，波速为500 m/s时减小程度最大，分别达27%、7%；考虑行波效应，主梁跨中竖向位移响应结果与纵向位移响应结果相反，行波效应会增加主梁跨中竖向位移，波速为500 m/s时，主梁跨中竖向位移比一致激时大2.55倍。综合分析，行波效应对主梁跨中和塔顶纵向位移的影响较小，对结构有利。但主梁跨中竖向位移增幅较大，不利于结构抗震，设计时应重视。

6 结论

(1) 地震波波速为500 m/s时，考虑行波效应时，大跨度双塔斜拉桥的索力响应峰值大于一致激励下索力峰值，但随着波速的增大，行波效应对拉索索力的影响减弱，并最终接近于一致激励下响应结果。

(2) 随着地震波波速的增大，行波效应对桥梁结构位移和内力的影响减小，并最终接近于一致激励下响应结果。

(3) 行波效应对各墩/塔底内力的影响不相同，与一致激励相比，有些部位的响应总体递减，而有些部位的响应有增有减；低波速对墩/塔底内力的影响最明显。

(4) 考虑行波效应，主梁跨中和塔顶的纵向位移较一致激励下减小，对结构有利。但主梁跨中竖向位移增幅较大，不利于结构抗震，设计时应予以重视。