复合材料导管导流罩渐进失效分析
李 彬,朱枭猛,陶江平,孙宜强
(1.上海交通大学 船舶海洋与建筑工程学院,上海 200240;2.上海船舶工艺研究所,上海 200032;3.中国船舶及海洋工程设计研究院,上海 200011)
0 引 言
导管是在船舶推进系统中起导流、支撑和保护作用的重要组合构件。导流罩作为导管内部的关键支撑连接结构,其设计需要综合考虑结构力学、空气动力学及结构质量等方面的严格要求。复合材料作为新型材料的代表,具有比强度大、比刚度高和耐腐蚀性好等多个性能特点。与传统金属结构相比,在等强度和刚度条件下,复合材料质量大幅减轻,这对导管和船舶结构性能优化及减重具有重要意义。复合材料具有多层次性与各向异性,其结构破坏机理不同于传统金属材料。层合板完全破坏并非瞬间发生,其结构失效是内部材料失效累积、由量变到质变的过程。在逐渐增加的载荷作用下,复合材料层合板各层所处应力状态不同。最先达到强度极限的单层首先破坏,破坏单层刚度随之减小,称为刚度降级。整个层合板结构虽未失效,但刚度随之折减,应力重新分配。继续增加载荷,会出现新的破坏层,刚度进一步降低,如此反复直至结构完全失去承载能力,层合板则达到极限强度。
刚度降级是复合材料失效过程中的宏观表现,在进行复合材料结构渐进失效分析时,连续损伤力学(Continuum Damage Mechanics,CDM)理论可较好地解释刚度降级的原因。材料损坏状态可用损伤变量描述。随着损伤力学的发展,通过定义损伤张量及损伤演化规则,对纤维增强复合材料进行多种损伤变量定义。在CDM理论下,文献[1]~文献[4]引入内部状态变量分析纤维增强复合材料结构损伤演变,旨在将损伤机制的力学特性与各种损伤状态所需要的耗散能量联系起来。文献[5]通过将CDM理论与有限元方法联系起来,将热力学理论应用于复合材料层合板损伤演化的模拟。但这些热力学模型仅限于二维平面结构。文献[6]采用考虑几何非线性和损伤演化的CDM理论方法,研究受内/外压力作用的层合复合材料浅圆柱形和锥形板的静态响应特性和破坏载荷。文献[7]和文献[8]结合CDM理论推导受损材料的本构关系。
基于上述思想,结合CDM理论和以能量为基准的刚度降级方法,采用渐进失效分析方法从材料失效角度对复合材料导管导流罩极限承载能力问题进行研究。结合层合板失效试验与仿真结果对比,验证利用Tsai-Wu失效准则对材料损伤及损伤原因进行判定的可行性。依据设计参数建立导流罩有限元模型,应用多帧重启动分析及弧长法对模型进行求解。在渐进加载过程中针对每个单元进行失效判定和刚度折减,实现失效过程的细观模拟。研究方法可预测复合材料导流罩的破坏载荷,并为研究复合材料导管结构典型区域失效演变规律奠定理论基础。
1 CDM理论
1.1 失效准则
材料损伤及损伤原因判定结合Tsai-Wu失效准则。对于各向异性复合材料层合板,失效准则通过如下公式[9]进行定义:
(1)
式中:σ1和σ2分别为材料纵、横向应力分量,纤维方向为纵向1方向,垂直于纤维方向为横向2方向;σ6为主方向剪切应力。
张量项系数由如下公式得到:
(2)
式中:Xt和Xc分别为纵向拉伸、压缩强度;Yt和Yc分别为横向拉伸、压缩强度;S为剪切强度。
Tsai-Wu失效准则可判断单元失效,但无法判定单元的失效模式。因此,从Tsai-Wu失效准则中分离3个组合变量Hi(i=1,2,6),由变量最大值判断单元的主导破坏模式。在H1为最大值时,表示纤维断裂为主要破坏模式;在H2为最大值时,表示基体开裂为主要破坏模式;在H6为最大值时,表示界面剪切失效为主要破坏模式。
(3)
1.2 刚度降级模型
CDM理论将结构损伤与其对工程常数的影响联系起来,引入损伤状态变量表达复合材料的不同失效模式,根据失效模式的不同对材料积分点处刚度矩阵进行降级,模拟复合材料的失效演变情况[10]。

(4)
式中:0≤D≤1,D在数值上代表结构中的微裂纹分布密度,说明有效承载面积的缩减比例;在D=0时,材料没有损伤;在D=1时,材料完全失去承载能力。
根据CDM理论,材料损伤后的单层应力应变关系可由如下公式表示:
(5)

在材料主轴方向刚度降级时,任意方向单层刚度随之下降。每个损伤状态变量均与共轭力有关,而共轭力由相应方向的应力应变状态决定,具体公式推导过程可参考文献[12]。
在纤维断裂失效时,相应的损伤状态变量D1相关的共轭力Y1为
(6)
式中:We为损伤材料的弹性应变能密度;D1可通过指数形式进行定义,即
D1=1-exp[-kf(Y1-Y1c]
(7)
式中:kf为与材料相关的常数;Y1c为在纤维断裂时共轭力的临界值。
在基体开裂失效时,相应的损伤状态变量D2及相关的共轭力Y2为
(8)
(9)
式(9)中:h为与材料相关的常数;Y2c为对应基体开裂的临界共轭力。
对于界面剪切失效情况,共轭力Y6及损伤变量D6由如下公式计算得出:
(10)
(11)
式(11)中:Y60为对应界面失效的临界共轭力;Y6c为D6=1时的共轭力临界值。
数值分析流程如图1所示,其中:P=P0+ΔP表示测试拉力每一步递增ΔP。为实现上述复合材料结构渐进失效数值模拟,采用有限元方法对结构进行离散。逐渐增加载荷并随每个载荷步进行失效模式判定、失效单元统计及刚度降级,直至整体结构最终失效。

图1 失效分析流程
2 渐进失效试验
为验证渐进失效分析方法对复合材料导管导流罩强度预测的可行性,对层合板进行基于CDM理论的渐进失效分析,得到层合板模拟拉伸试验的载荷位移曲线及失效单元数目随外力变化情况,并将仿真分析结果与层合板试件拉伸试验结果对比以证明该方法的合理性。试件尺寸及铺层角如图2所示,试件采用T300碳纤维增强树脂基复合材料,[0°,90°]正交四层对称铺设,试件厚度h为2.50 mm,宽度b为25.00 mm,除去两端夹持固定位置中间有效测试段长l为150.00 mm。复合材料试件材料属性如表1所示,其中:E1、E2、μ12和G12分别为纤维方向弹性模量、纤维横向弹性模量、泊松比和剪切模量。
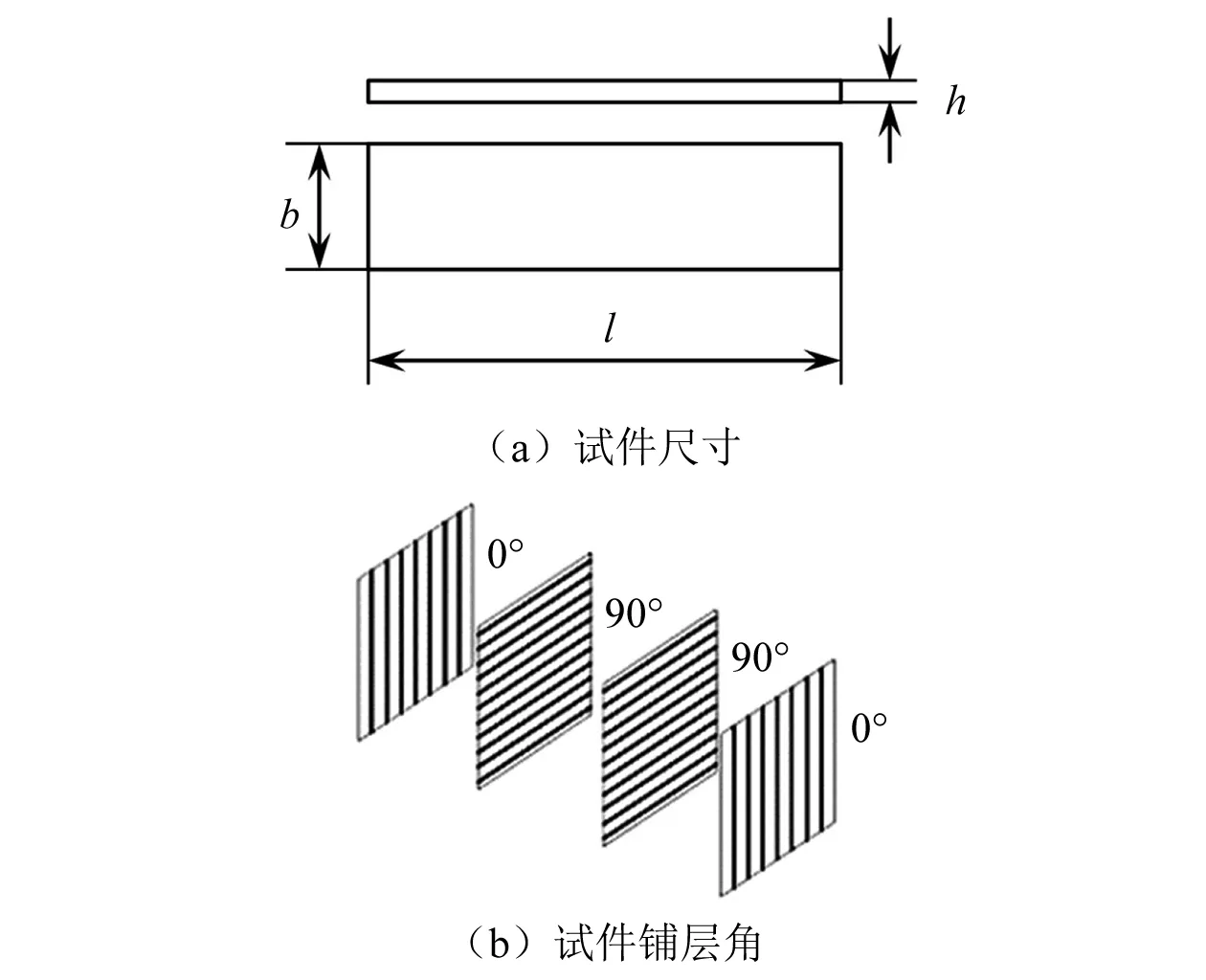
图2 试件尺寸及铺层角

表1 复合材料试件材料属性
利用ANSYS有限元分析软件编写APDL子程序,使其具备渐进失效分析功能。为对层合板结构内各位置进行分析,采用SOLID185单元对各层结构进行离散;为应用上述渐进失效模型,利用宏命令对每个单元在每一步迭代过程中赋予材料属性。各单元的失效判据选用Tsai-Wu失效准则,具体失效分析过程如图1所示,应用多帧重启动分析及弧长法对模型进行求解。
重启动分析是一种在求解结果的基础上进行分析的方法。在非线性静态分析中,多帧重启动允许在运行过程中的诸多子步保存分析信息,并在这些子步进行重启动分析。在初次分析中需要对载荷子步进行设置。在重启动时,使用ANTYPE命令设置重启动的载荷点和重启动分析类型。带有重启动分析的整体流程主要包括6个方面:有限元建模;初始分析;后处理1;重启动初始分析;重启动再分析;后处理2。
弧长法是一种非线性迭代求解控制方法,可解决在载荷和位移增量均不确定的情况下产生变化的增量值问题,同时追踪结构加载路径。通过命令或菜单操作可激活弧长法并设置弧长半径的最小和最大乘数。弧长半径参考值可由第1个子步的第1个迭代中求解的载荷或位移增量计算而来。在每个随后的子步计算时,首先计算1个新的弧长半径,新的半径基于上一子步的弧长半径和求解状况;随后,这个新的弧长半径进一步被修正,以保证其处于上下限之内。在最小半径无法收敛时,弧长法自动停止。
试件模型一端刚性固定,另一端仅保留试件长度方向平动自由度。初始加载拉力为3 kN,载荷增量为1 kN,采用牛顿-拉普森方法进行多帧重启动分析。计算得到失效单元数目随载荷增加变化过程,如图3所示。随着载荷增加,最先出现的失效模式是基体开裂;在拉伸试验加载过程中试件发出响声,意味逐渐出现破坏,加载过程中的数值模拟可模拟试验过程;在拉力接近断裂载荷时出现纤维断裂失效模式,在纤维断裂大规模出现时,试件完全失效。在加载过程中没有出现界面剪切失效模式。计算得到模型断裂载荷为32 kN。
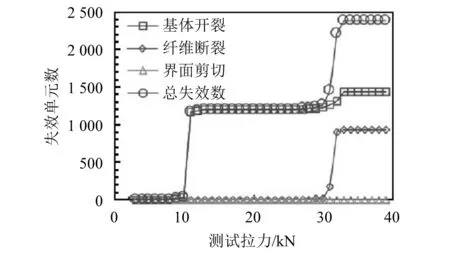
图3 失效单元数目随载荷增加变化过程
模型即将完全破坏时的各层单元损伤类型分布如图4所示。上下两层由于纤维方向与受力方向相同,具有较大的强度和刚度,因此在加载过程中没有出现破坏。在模型即将破坏时,端部出现单元失效,包括纤维断裂及基体开裂两种模式,并随加载过程失效部分向外扩展,端部单元完全失效。端部单元失效演变过程如图5所示。

图4 单元损伤类型分布
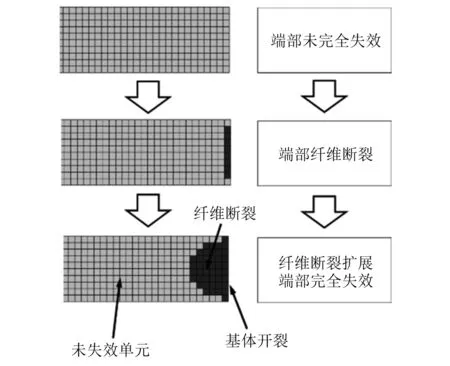
图5 端部单元失效演变过程
为验证复合材料层合板失效数值分析方法的可行性,对层合板进行拉伸试验并将试验结果与数值分析结果进行对比。单向拉伸选取3个试件重复测量以降低误差。测试拉力分级加载,每级载荷相差为断裂载荷的5%~10%,连续增加载荷直至试件被拉断,记录试件拉断时的最大载荷。试件1断裂载荷为29 743 N,试件2断裂载荷为29 170 N,试件3断裂载荷为29 841 N。试件断裂情况如图6所示。在试验中,试件实际断裂位置发生在有效测试段的端部,由于试件端部为试验机夹持部位,因此在试验后为观察复合材料破坏情况将两端金属片取下。数值计算中的试件端部失效情况与之相符。试验断裂载荷平均值为29 585 N,数值计算结果与之相比误差为8.2%。试验结果验证复合材料层合板失效数值分析的准确性。

图6 试件断裂情况
3 渐进失效分析
复合材料导流罩失效机理复杂,材料失效导致导流罩发生破坏、失去承载能力。基于材料失效理论在复合材料层合板失效分析中的应用,从材料失效角度对导管导流罩结构失效机理进行预测。导流罩整体采用T700碳纤维增强树脂基复合材料薄壁锥形结构,铺层角度为[0°,[45°,-45°]3,90°]sym(sym代表对称铺设),单层厚度约0.35 mm。导流罩材料性能参数如表2所示,强度参数如表3所示,损伤参数如表4所示。

表2 导流罩材料性能参数

表3 导流罩材料强度参数 MPa

表4 导流罩材料损伤参数
基于CDM理论,按照图1流程顺序,利用APDL编写考虑刚度降级的参数化语言,对复合材料导管导流罩进行渐进失效分析。为准确分析各层内部及层间应力状态,整体结构采用SOLID185实体单元离散,划分80 000个复合材料单元,并按顺序进行编号。碳纤维复合材料为各向异性材料,在定义材料属性时根据各铺层角度和单向板工程常数计算复合材料单元在整体坐标系下的材料刚度矩阵,通过定义刚度矩阵确定复合材料单元材料属性。假设各层间完全粘接,复合材料导管导流罩有限元模型如图7所示。导流罩大端六自由度约束,对导流罩模型小端截面施加初始载荷F0,并确定没有发生失效,对复合材料单元分别定义材料、损伤变量Di(i=1,2,6)和共轭力Yi(i=1,2,6)。对模型进行小跨度逐级加载,每个载荷步采用多帧重启动分析。随着导流罩小端截面逐步加载,监控各单元应力应变并利用Tsai-Wu失效准则对单元失效进行判定,由共轭力进一步推导确定失效模式。在发生失效后对Di(i=1,2,6)进行修正,并进行刚度降级,循环直至导流罩结构最终失去承载能力。
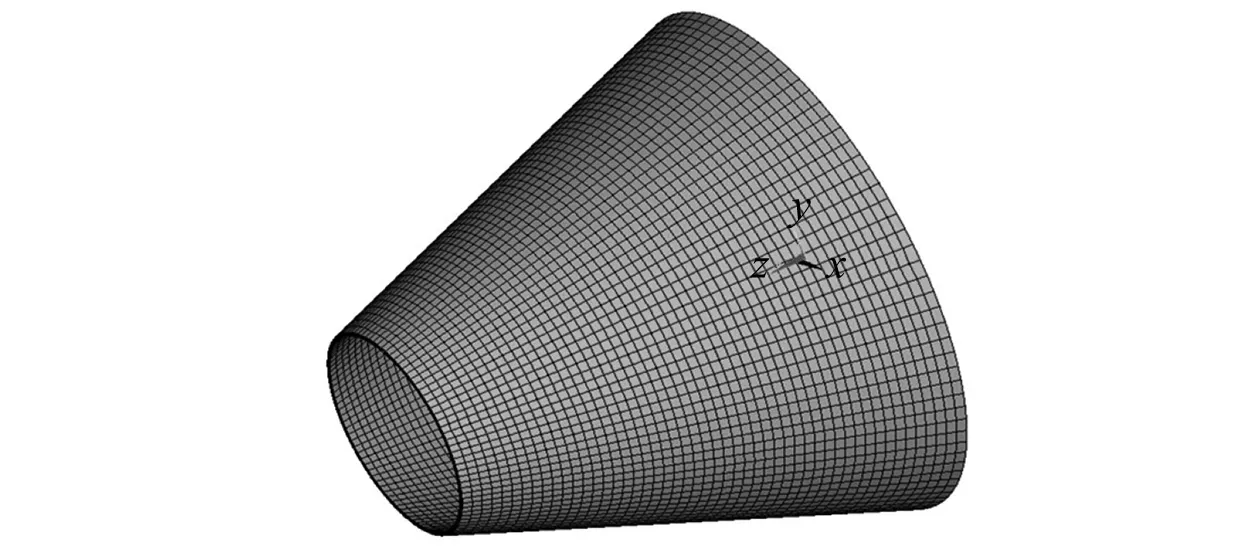
图7 导流罩有限元模型
4 计算结果分析
导流罩失效单元数随载荷增加而变化,如图8所示。导流罩在140 kN出现初始失效,最先发生基体开裂失效模式。此后,随着载荷继续增大出现纤维断裂失效模式,在纤维断裂大规模出现时,导流罩结构失去承载能力。
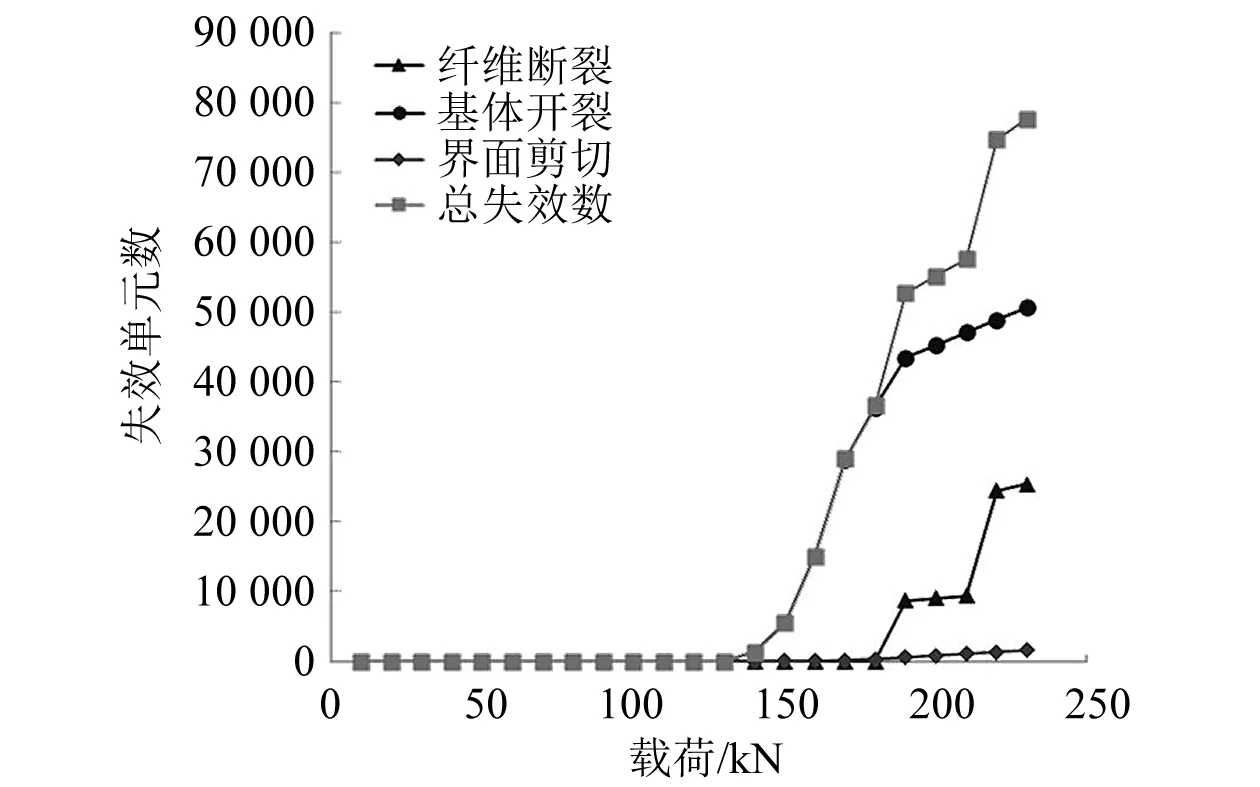
图8 导流罩失效单元数
导流罩载荷位移曲线如图9所示。由图9可知:

图9 导流罩载荷位移曲线
导流罩在加载初始阶段没有失效,载荷与位移呈一定线性关系;随着载荷增加,虽出现单元失效,但外载荷与位移非线性关系仍不明显;在纤维断裂出现时,非线性关系逐渐明显,随着载荷增加,位移急剧变化。基于CDM理论的失效分析显示,导流罩的破坏载荷为230 kN。
有限元模拟采用标准单位,即m-kg-s单位制。图10~图13的位移单位为m,应力单位为Pa。即将失效的导流罩位移云图如图10所示,导流罩最大变形量为20.75 mm,最大变形发生在导流罩小端,位移向导流罩轴向延伸。导流罩单元失效过程如图11所示:导流罩结构最先出现基体开裂,随着载荷增大出现纤维断裂;纤维断裂最先出现在靠近小端位置,随后逐渐向大端蔓延;在纤维断裂大规模出现时,达到其极限承载能力;在最大变形位置附近出现多种失效类型;由于各层材料方向不同,因此出现不同的失效演变过程。导流罩未发生失效的等效应力如图12所示。导流罩结构完全失效前的等效应力如图13所示:最大应力发生在导流罩小端,在最大应力附近具有多种失效模式。

图10 即将失效的导流罩位移云图

图11 导流罩单元失效过程

图12 导流罩未发生失效的等效应力

图13 导流罩结构完全失效前的等效应力
5 结 论
基于CDM理论,结合以能量为基准的刚度降级方法,对复合材料导管导流罩进行渐进失效分析,从材料失效角度对其极限承载能力及失效演变情况进行研究,可得到:
(1)单向拉伸板和导流罩均会产生在达到某一外力时立刻出现大量失效单元或随外力增大失效单元数目增加较快的情况。
(2)导流罩最先出现基体开裂失效模式,此时少量破坏对导流罩整体结构性能影响较小;随着载荷继续增加,出现纤维断裂失效模式,在纤维断裂大规模出现时,载荷位移非线性关系逐渐明显,结构性能急剧下降;整个过程几乎没有出现界面剪切失效情况。
(3)导流罩最大位移和应力均发生在导流罩小端,在小端位置附近出现多种失效类型;各层铺层角不同,失效演变过程不同。

