基于博弈论的汛期小浪底-西霞院-下游河道水沙资源优化分配研究
王 欣,唐凤珍,李 想,王远见
(1.黄河水利委员会 黄河水利科学研究院,河南 郑州 450003; 2.水利部黄河下游河道与河口治理重点实验室,河南 郑州 450003; 3.中国水利水电科学研究院 流域水循环模拟与调控国家重点实验室,北京 100038)
长期以来,黄河以“水少沙多,水沙异源,水沙关系不协调”著称于世[1-2]。 其中“水沙关系不协调”是当前黄河亟待解决的核心问题[3],相应的解决措施应是增水[4]、减沙[5]与调水调沙[6],以塑造与黄河相适应的协调水沙关系。 在汛期和汛前调水调沙过程中,如果将洪水和泥沙的利害两面均考虑进来,则水沙资源在水库群及下游河道之间如何分配就变成了一个典型的利益分配问题。 由于各利益主体(各水库、河道管理部门)分属不同单位且具有各自的利益需求,与传统的定量分析方法和最优化方法仅考虑全局最优解相比,博弈论方法能够将各利益主体的需求考虑进来,因此博弈论方法在该问题求解中具有独特的优势[7]。
目前,国内外专家对基于博弈论的水资源优化配置进行了大量研究,如Dombrowsky[8]理论分析了跨境河流不同用水户之间水资源互利所需的激励机制和制度前提,验证了多人博弈模型的效益共赢假说;Bai等[9]以龙羊峡水库和刘家峡水库为研究对象,分析了多种流量调节模式下的梯级水库优化联合调度的协同效益;Li 等[10]以水库发电、生态需水及农业灌溉为综合目标函数,研究了丰、平、枯水年不同来水条件下澜湄(澜沧江和湄公河)流域跨界水资源协同博弈情景;Yu 等[11]通过GAMS 建模优化发电调度和生态流量,通过WEAP 模型模拟澜湄流域下游五国农业供水量,分析了澜湄流域跨境水量-水能-生态互馈关系;苏心玥等[12]利用改进的纳什讨价还价博弈模型,结合破产理论,加入跨区水资源的时空约束规则,分析了不同的供水情景和博弈权重组合方案下北京市未来水资源配置的合作博弈稳定性与系统可持续性;Janjua 等[13]以巴基斯坦境内印度河流域水资源分配为研究对象,通过对比传统优化算法与纳什讨价还价算法计算结果,构建了水外交框架(WDF)来解决水资源供需不匹配的问题;Rahaman 等[14]采用合作博弈理论,研究了孟加拉国和印度共有的提斯塔河流域内水电开发潜力;蔡方园等[15]构建了澜沧江干流水库发电效益与生态-出境水的完全信息静态博弈模型,并分析了水库发电效益与生态-出境流量之间的竞争博弈关系;宗鑫[16]构建了跨区域协同保护逐级自愿协商平台及协商层次,对相关利益主体间协商博弈行为进行了分析;王淏等[17]以澜沧江水电为例研究构建了梯级电站优化调度模型和水电-火电合作博弈模型,提出了改进的夏普利值法对博弈利益进行再分配;付湘等[18]对比分析了讨价还价博弈模型与主从博弈模型在水资源利用与排污控制方面的优劣,为水资源利用与水环境保护冲突管理提供了新的协调方法。 但由于水沙关系复杂、水沙联调基本理论尚不成熟以及博弈论理论体系与博弈模型构建求解过程较为复杂等,因此目前基于博弈论解决多沙河流不同利益主体之间水沙资源配置冲突方面的研究较少[7]。 本文基于博弈论原理,以小浪底水库、西霞院水库及下游河道为博弈主体,构建小浪底-西霞院-下游河道(以下简称“小-西-下”)水沙资源分配博弈模型,计算不同博弈情景下模型计算结果,并对大联盟合作情景下小浪底、西霞院、下游河道三方效益进行再分配,以期为利用博弈论实现小-西-下水沙资源优化分配提供参考。
1 模型构建
小-西-下水沙博弈调度实质上是一个复杂大系统的多目标优化问题。 本研究在模型构建和求解时,将防洪目标、供水目标、生态环境目标转化为约束条件,从而将黄河干流骨干枢纽群调度问题转化为发电、排沙、河道减淤这3 个目标,即保证发电目标、排沙目标和减淤目标最优。 其中,西霞院水库由于设计库容较小,在研究小-西-下动态博弈模型时不考虑其拦沙功能,因此博弈模型中的西霞院水库效益函数只考虑发电效益,无淤损效益。 考虑到小浪底和西霞院两水库排沙对下游河道防洪安全带来的危害,因此下游河道的效益函数只考虑下游河道的淤损效益。
1.1 不同博弈情景设置
根据汛期小浪底、西霞院、下游河道水沙联合调度实际情况可知,小-西-下水沙资源分配博弈可出现3种博弈类型,具体包括4 种博弈情景(见表1):大联盟合作博弈(小浪底、西霞院、下游河道均选择合作),单独博弈(小浪底、西霞院、下游河道均选择不合作),局部合作博弈(小-西合作、西-下合作)。 不同博弈情景下,博弈三要素不同,但博弈模型的战略集均与小浪底水库(水库1)、西霞院水库(水库2)第i天的日均出库流量Q1,i、Q2,i有关。

表1 小-西-下水沙资源分配博弈模型中多情景设置
1.2 水沙联合调控计算
以小-西-下水沙调控单独博弈情景为例,构建小-西-下水沙资源分配博弈模型及数学表达式。
1.2.1 小浪底水库
效益函数:
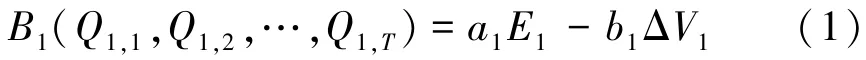
式中:a1、b1分别为水浪底水库效益折算系数(数值见表2);E1为小浪底水库的发电效益,亿kW·h; ΔV1为小浪底水库的累计淤积库容,亿m3;T为实测期,d。
(1)发电效益。E1计算公式为
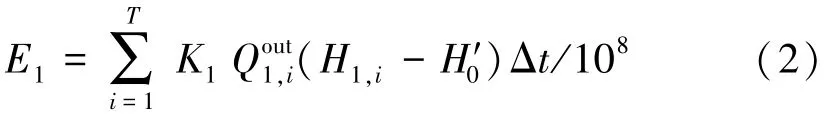
式中:K1为小浪底水库电站出力系数;Qout1,i为小浪底水库第i天的日均过机流量,m3/s;H1,i为小浪底水库第i天坝前平均水位,m;H′0为小浪底水库发电洞高程,为
135.8 m;Δt为计算时段时长,本文取24 h。
其中,小浪底水库第i天坝前平均水位可通过对小浪底水库水位—蓄水量关系曲线进行线性拟合得出:
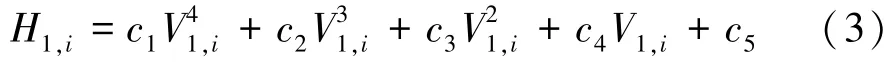
式中:V1,i为小浪底水库第i天蓄水量,亿m3;c1、c2、c3、c4、c5均为待定系数(数值见表2)。
(2)淤损效益。 ΔV1计算公式为
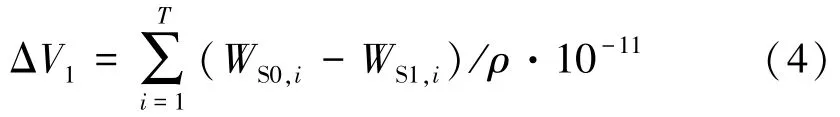
式中:WS0,i、WS1,i分别为实测期内小浪底水库第i天的入库沙量、出库沙量,t;ρ为水库淤积泥沙干容重,本文取2 650 kg/m3。
根据水量平衡法则,构建蓄水量—流量关系如下:
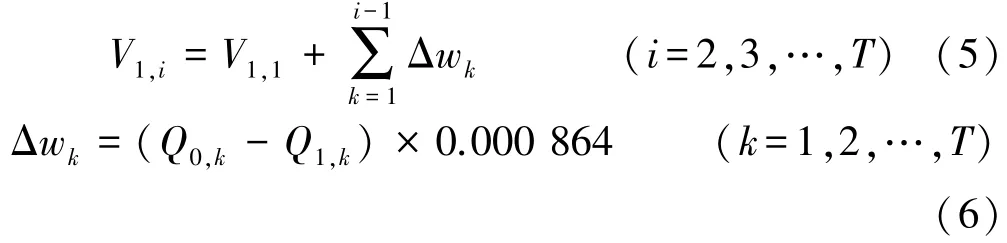
式中:V1,1为小浪底水库实测期内第1 天蓄水量,亿m3;Δwk为第k天小浪底水库蓄水量变量,亿m3;Q0,k为第k天小浪底水库日均入库流量,m3/s;Q1,k为第k天小浪底水库日均出库流量,m3/s。
根据小浪底水库汛期排沙比经验公式[19],构建出库沙量—流量关系如下:
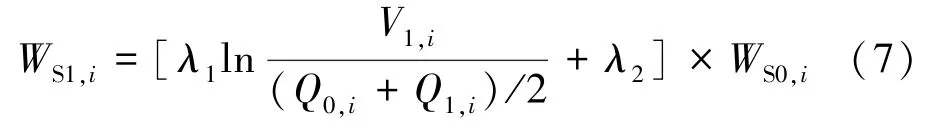
式中:λ1、λ2分别为待定系数(数值见表2)。
1.2.2 西霞院水库
效益函数:
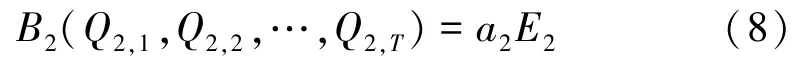
式中:a2为西霞院水库效益折算系数(数值见表2);E2为西霞院水库的发电效益,亿kW·h。
(1)发电效益。E2计算公式为
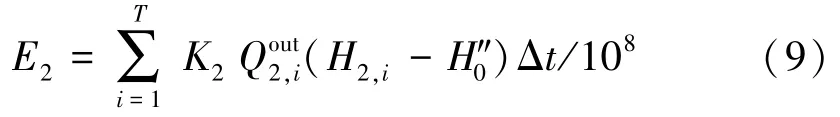
式中:K2为西霞院水库电站出力系数;Qout2,i为西霞院水库第i天的日均过机流量,m3/s;H2,i为西霞院水库第i天坝前平均水位,m;H0″为西霞院水库发电洞高程,为120.2 m;Δt为计算时段时长,本文取24 h。
西霞院水库水位—蓄水量关系式如下:
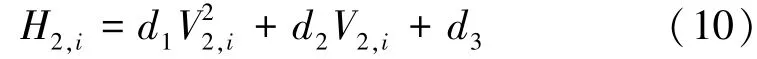
式中:V2,i为西霞院水库第i天蓄水量,亿m3;d1、d2、d3分别为待定系数(数值见表2)。
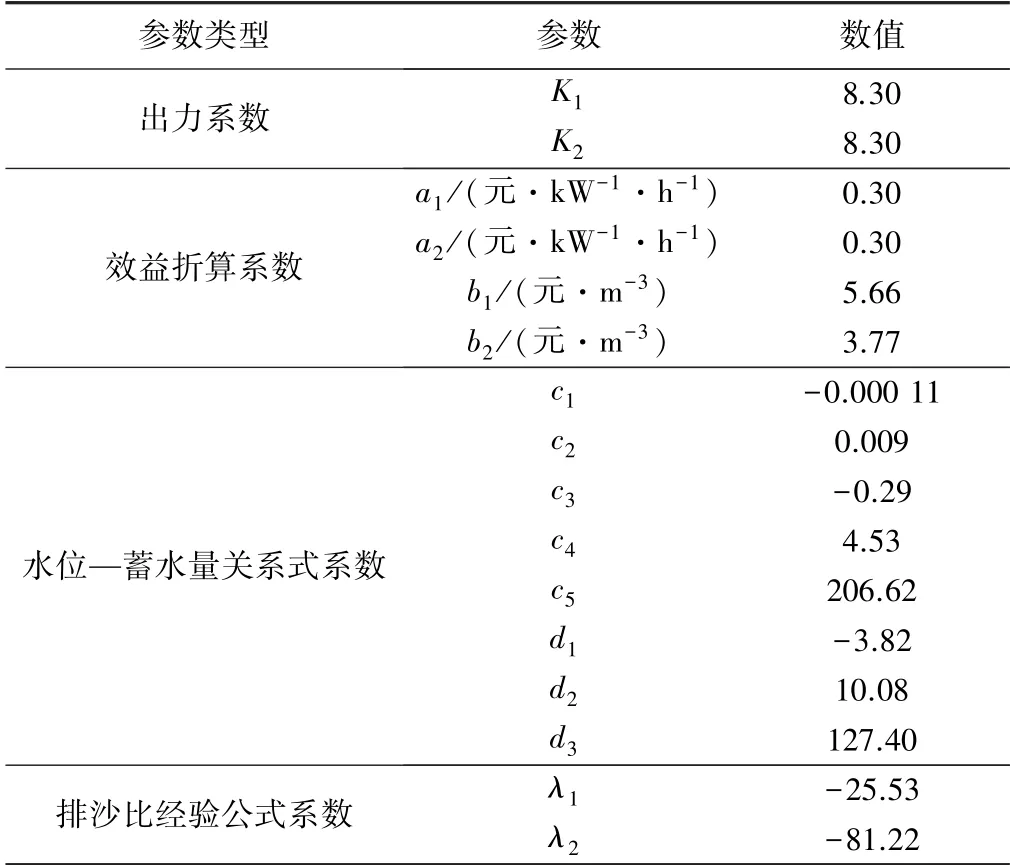
表2 水沙联合调控模型主要参数
(2)蓄水量—流量关系(水量平衡法则)。 公式为
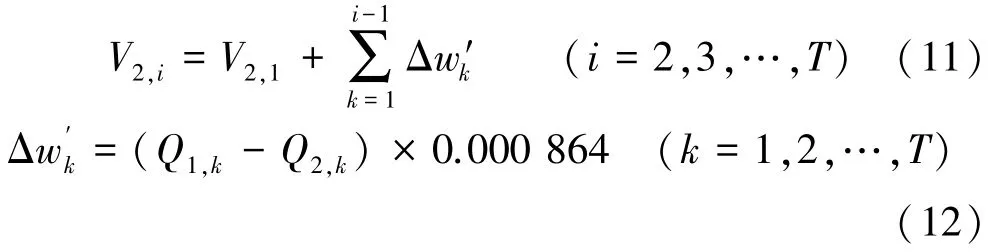
式中:V2,1为西霞院水库实测期内第1 天蓄水量,亿m3;Δw′k为第k天西霞院水库蓄水量变量,亿m3;Q2,k为第k天西霞院水库日均出库流量,m3/s(假设小浪底与西霞院之间无支流汇流,即小浪底出库水沙条件即为西霞院入库水沙条件)。
1.2.3 下游河道
效益函数:
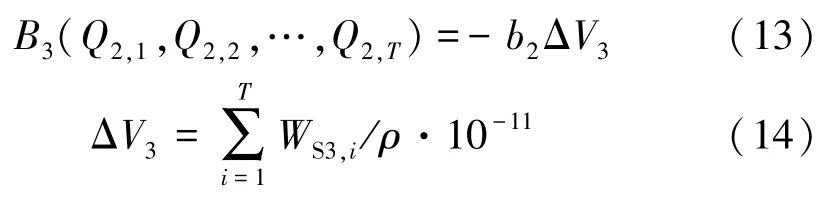
式中:b2为下游河道效益折算系数;ΔV3为下游河道淤积沙量,亿m3;WS3,i为下游河道第i天淤积量,t。
根据下游河道日淤积量经验公式[20],构建出库沙量—流量关系如下:
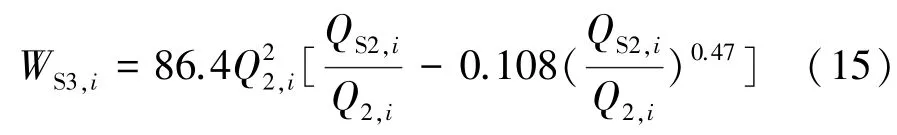
式中:QS2,i为西霞院水库第i天日均出库含沙量,kg/m3。
1.3 约束条件与初始条件
(1)水位约束。 表达式为
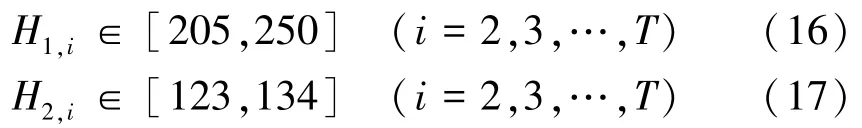
为满足防洪要求,根据历年汛期实测数据,小浪底、西霞院日均坝前水位变化范围分别为[205,250]、[123,134]。
(2)下泄流量约束。 表达式为
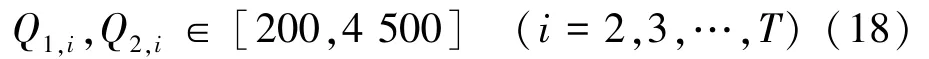
水库下泄流量的下限根据下游供水和生态需水的要求综合确定,上限由下游汛期防洪安全要求确定。为满足防汛和生态流量的需求,两水库汛期日均出库流量应在200~4 500 m3/s 范围内。
(3)优化调度约束。 表达式为

优化调度方案应满足与真实调度情景下的初末水位相同,即水量平衡。H′1,1、H′1,T分别为小浪底水库真实调度情况下的初、末水位,m;H′2,1、H′2,T分别为西霞院水库真实调度情况下的初、末水位,m。
(5)初始条件。 以潼关水文站2019 年7 月1 日至8 月31 日(共62 d)实测水文数据为模型输入数据来源。 小-西-下水沙联合调控模型初始条件变量见表3,其中初始蓄水量、初始水位分别为2019 年7 月1 日实测蓄水量及水位,期末水位为2019 年8 月31 日实测水位。

表3 水沙联合调控模型初始条件变量取值
2 模型运用
2.1 不同博弈情景下模型计算结果
对三博弈方大联盟合作博弈、单独博弈、局部合作(小-西合作,西-下合作)及2019 年三博弈方真实运行过程等不同情景下的博弈方案进行计算,得出结果见表4。

表4 不同博弈情景下博弈模型计算结果
由表4 可知,不同博弈情景下的小-西-下水沙分配动态博弈结果均略优于真实运行过程,这说明真实调度过程已经接近于优化调度结果。 在全局角度上(即集体理性),大联盟合作博弈情景下的小-西-下水沙资源分配效果最好(综合效益为11.861亿元),单独博弈情景下水沙分配效果最差(综合效益为11.671 亿元)。 在个体效益最优角度上(即个体理性),不同博弈方的效益最优及最差博弈方案不同。 其中:小浪底水库在不与下游河道合作的情景下(即除参与大联盟合作博弈之外),效益均为最优(24.310 亿元);西霞院水库在小-西合作情况下效益最优(0.477 亿元),在大联盟合作情景下效益最差(0.394 亿元);下游河道在大联盟合作博弈下效益最优(-12.579 亿元),在单独博弈或小-西合作情况下效益最差(-13.114 亿元)。不同博弈情景下三博弈方的水沙资源分配情况如图1所示。
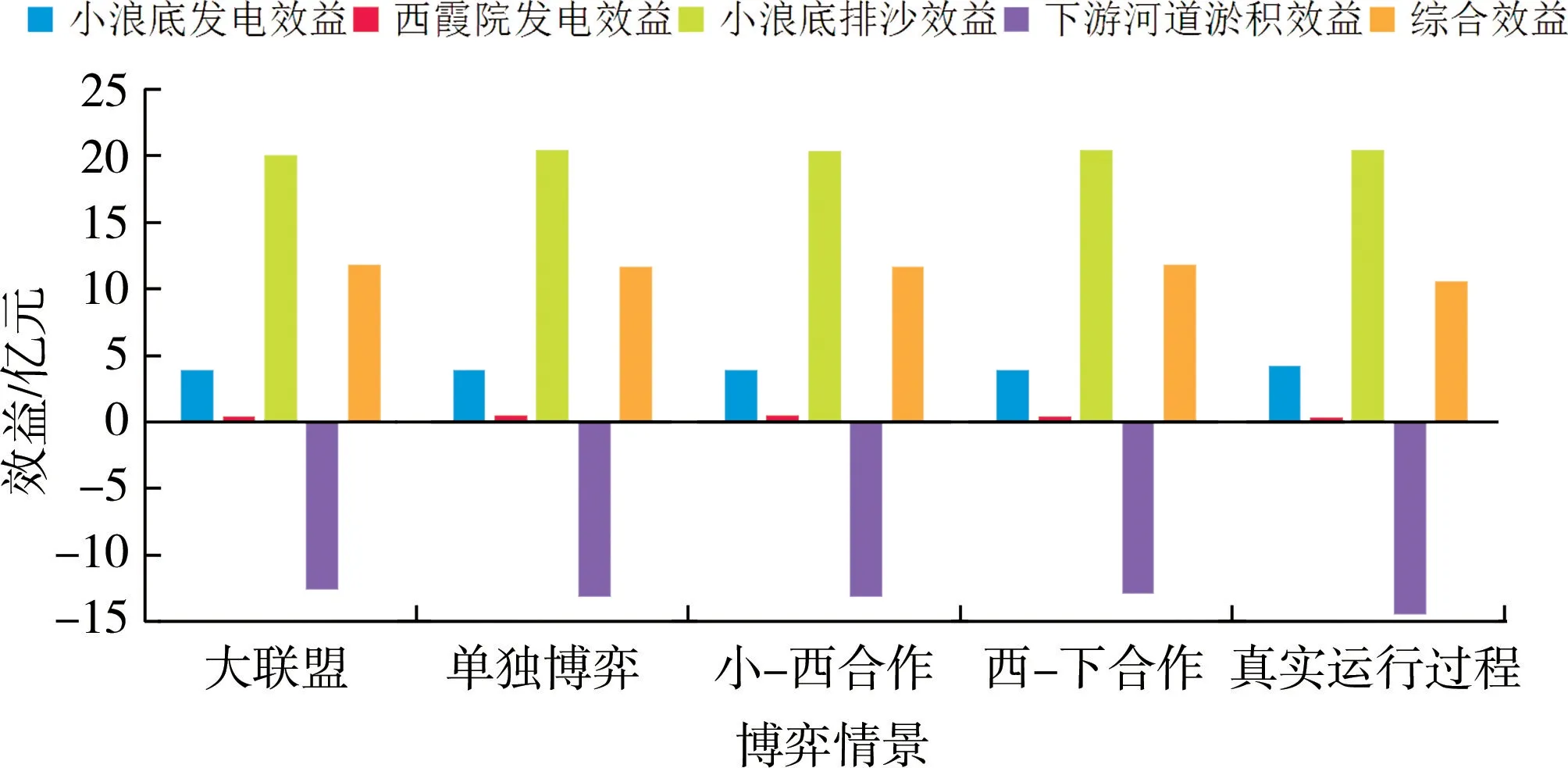
图1 不同博弈情景下水沙资源分配情况
根据博弈均衡原理可知,在没有其他干预(如上级流域管理机构干预、不同博弈情景下各博弈方同意进行效益再分配等)的情况下,根据个体最优原则,在2019 年汛期实际水沙调度过程中,小浪底水库的最优战略为“不与下游河道合作”,即单独博弈({小,西,下})或与西霞院水库单独结盟构成“小-西合作”({(小,西),下});西霞院水库的最优战略为“与小浪底单独结盟构成小-西合作”({(小,西),下});下游河道的最优战略为“加入大联盟合作博弈”({(小,西,下)})。 考虑到真实调度过程中,小浪底水库与西霞院水库属于同一家水电公司管理,因此在2019 年汛期水沙条件下小浪底水库、西霞院水库与下游河道水沙资源动态博弈结果应为“小-西合作”,即三者的效益分别为24.310 亿、0.477 亿、-13.114 亿元。
2.2 效益重分配情景下博弈模型计算结果
为进一步研究小-西-下水沙博弈情景的可能性,本研究选取两种常见的博弈模型效益再分配计算方法即Shapley value 法[21]、Gately point 法[22],对大联盟合作博弈情景下的小浪底、西霞院、下游河道效益进行再分配,计算结果见表5。
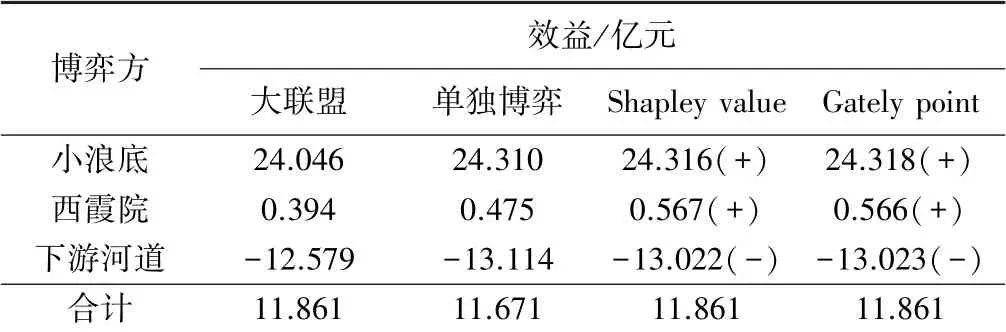
表5 不同效益再分配方法下博弈模型计算结果
考虑各利益主体(各水库、河道管理部门)的分属单位,整理小浪底水库、西霞院水库、小-西利益共同体及下游河道可接受博弈情景见表6。
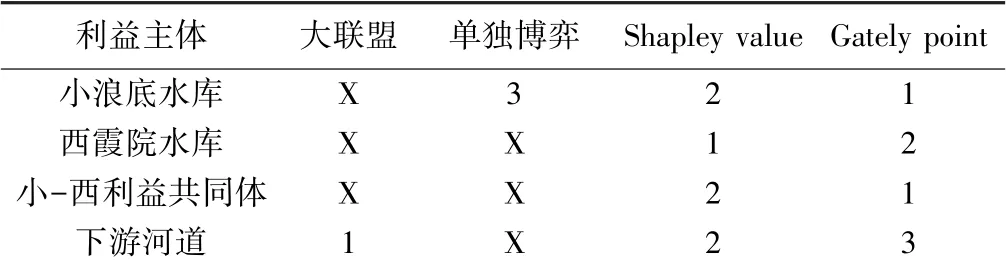
表6 小-西-下可接受博弈情景
由表6 可知,如果将小浪底水库、西霞院水库作为利益共同体考虑,小-西利益共同体倾向于选择“大联盟+Gately point 法”。 对下游河道而言,“大联盟+Gately point 法”虽不是其最优选择,但仍优于下游河道不加入小-西合作时的效益(-13.023 >-13.114)。根据同一流域水沙资源分配特性可知,位于上游的决策方具有优先决策权,因此最终推荐的利益再分配方法为Gately point 法。 若小浪底、西霞院之间具有较强合作约束力,则在2019 年汛期水沙条件下小浪底水库、西霞院水库与下游河道水沙资源动态博弈情景应为“大联盟+Gately point 法”,即三者的效益分别为24.318亿、0.566 亿、-13.023 亿元。 相比无约束前提下的“小-西合作”情景,小浪底水库、西霞院水库及下游河道采用“大联盟+Gately point 法”后整体效益提升1 880万元。 其中:小浪底水库运行综合效益提升80万元,西霞院水库运行综合效益提升890 万元,下游河道减淤效益提升910 万元。 相比各自不合作情景,“大联盟+Gately point 法”情景下的三者整体效益提升1 900万元。 其中,小浪底水库运行综合效益提升80万元,西霞院水库及下游河道效益均提升910 万元。
3 结 论
本文运用博弈论研究了小浪底水库、西霞院水库及下游河道水沙资源优化分配情景及结果,得出如下结论。
(1)以2019 年汛期水沙条件为例,在没有外界条件及博弈方之间联盟约束等干预的前提下,小浪底水库、西霞院水库及下游河道水沙资源优化分配过程可近似为完全信息静态博弈。 根据个体理性原则,三者会选择“小-西合作”的战略。
(2)以2019 年汛期水沙条件为例,小浪底水库、西霞院水库及下游河道的最优决策方案为三者同意选择大联盟合作博弈战略,并达成协议利用Gately point法对大联盟合作博弈情景下的效益进行再分配(即“大联盟+Gately point 法”)。 相比“小-西合作”情景,整体效益提升1 880 万元;相比各自不合作情景,整体效益提升1 900 万元。 研究成果展现了博弈论在黄河流域水沙资源优化配置与水库群优化调度中应用的可行性和广阔前景。

