考虑等效井网密度的南海东部水驱砂岩油藏采收率预测
杨 勇 李 伟 唐 放 张 团 崔传智 钱 银 吴忠维
(1. 中海石油(中国)有限公司深圳分公司,广东 深圳 518067;2. 中国石油大学(华东)非常规油气开发教育部重点实验室,山东 青岛 266580)
0 引 言
采收率预测对水驱油藏开发调整及效果评价具有重要意义,目前关于水驱油藏采收率预测方法较多[1-10],主要包括统计方法[3-7]、水驱曲线[8]、产量递减曲线[9]及数值模拟方法[10]。水驱曲线、产量递减曲线均是从数据特征出发,获得油藏废弃时的累计产油量,从而获得采收率;水驱曲线、产量递减曲线预测采收率虽然矿场运用方便,但不能够反映储层物性、流体物性对采收率的影响。数值模拟方法通过建立相应的地质模型、渗流数学模型,运用数值求解获得相应的采收率;数值模拟方法能够较全面地考虑各因素(如流体物性、储层物性等)影响,但是操作复杂、时效性较差。统计方法预测采收率是通过运用统计学理论(如神经网络[3-4]、回归[5-7]等)建立采收率与储层物性、流体物性的关系,从而获得采收率;统计方法预测采收率不仅能够反映储层物性、流体物性对采收率影响,而且矿场运用简便;统计方法预测采收率需要大量实际数据,而南海东部水驱砂岩油藏群已开发多年,积累了丰富的数据,弥补了统计方法的缺陷。
目前关于陆相水驱砂岩油藏采收率预测的统计方法研究较多,但海相砂岩油藏采收率预测统计研究较少。冯沙沙等[7]针对陆相采收率统计公式不适用于海相砂岩油藏采收率预测的问题,基于南海东部砂岩油藏采收率数据,运用回归分析建立了边水与底水油藏采收率预测公式,但是该研究忽略了水平井与直井井型差异对井网密度影响,从而导致油藏采收率预测结果与实际偏差较大。南海东部砂岩油藏水平井与直井同时开发,由于水平井的生产能力一般远大于直井,在计算油藏井网密度时需要将水平井折算成直井。程林松等[11]通过对比水平井与直井稳态产量,首次提出了用于描述直井替代水平井的井数替代比,其定义为在总产量和总控制面积相同条件下所需水平井与所需直井井数的比值。张连枝等[12]将程林松等提出的井数替代比推广至分支井折算成直井的情况。以上井数替代比基于稳态产能公式,而实际开发过程为瞬态过程,用一个稳定状态去描述整个瞬态过程,结果势必会有误差。F.M.Giger[13]基于相同的泄油面积建立了另一种水平井与直井的替换比表达式,以泄油面积相等为条件计算替换比虽具有一定参考价值,但运用产能比更加合理。
本文首先运用数值模拟与回归分析方法,建立了水平井折算为直井的等效井数折算比计算模型,再结合南海东部水驱砂岩油藏地质与开发数据,建立了南海东部水驱砂岩油藏采收率预测模型,并通过与实际矿场数据对比验证了模型的准确性。该研究对南海东部水驱砂岩油藏的高效开发与措施调整具有重要意义。
1 计算模型
为弥补基于稳态产量提出的井数替代比忽略了瞬态开发过程的影响缺陷[11-12],将稳态产量修正为开发na 的累计产油量,n的取值与储层物性、流体物性及井控面积等参数有关。以开发na 后的水平井累计产油量与直井累计产油量之比(以下简称水平井—直井产能比)来表征等效井数折算比,该折算比从井的总生产能力角度出发,包括了整个瞬态开发过程对井生产行为,弥补了目前基于稳态产量的井数替代比的缺点:仅考虑某一状态去描述井的生产能力,不能够描述底水锥进、水平井各个流态等对产能影响,导致井数替代比误差较大。
针对南海东部水驱砂岩油藏储层物性及流体物性特征,首先在选取相应的累计产油量影响因素基础上,运用正交表获得影响因素在取值空间的均匀分布,其次运用数值模拟技术分别获得水平井—直井产能比,最后通过多元回归分析获得等效井数折算比模型。
1.1 水平井—直井产能比计算模型
通过文献调研发现[3-7]:油层厚度、水平渗透率(Kh)、垂向渗透率(Kv)与水平渗透率的比值、原油黏度、水平井水平段长度、井控面积、油藏能量等参数将影响水平井、直井的累计产油量。由于南海东部水驱砂岩油藏的水体能量充足,开发多年后的地层压力基本保持不变,且在计算水平井与直井的折算比时,需保持井控面积不变,因此,可以不用考虑油藏能量与井控面积这2 个因素。基于南海东部砂岩油藏物性参数,建立与其特征一致的边、底水油藏的油水两相概念模型(图1)。

图1 南海东部水驱砂岩油藏概念模型Fig.1 Conceptual models of waterflooding sandstone reservoirs in eastern South China Sea
水的黏度为0.28 mPa·s,水的压缩系数为0.363 GPa−1。由于南海东部海相砂岩油藏水体能量充足,依靠天然水驱能量开发,故通过设置Fetkovic(费特科维奇)水体来表征边、底水,水体倍数设为100 倍,模型网格数为100×100×n(n的取值与油藏厚度有关),网格尺寸为10 m×10 m×1 m,油藏厚度为4~16 m,水平井位于油层中间位置,水平渗透率为0.5~3.5 μm2,Kv/Kh(垂向渗透率/水平渗透率)为0.2~0.5;原油黏度为5~110 mPa·s;水平段长度为300~650 m。
针对以上分析获得的累计产油量影响因素油层厚度、水平渗透率、Kv/Kh、原油黏度和水平井水平段长度等,选取各影响因素的变化值(油层厚度分别为4、8、12、16 m;渗透率分别为0.5、1.5、2.5、3.5 μm2;Kv/Kh为0.2、0.3、0.4、0.5;原油黏度分别为5、40、75、110 mPa·s;水平段长度分别为200、350、500、650 m),各因素水平组合见表1。
各因素水平组合规律依据5 个因素4 个水平正交组合,共形成16 个方案。针对这16 个方案,运用数值模拟技术分别求取底水油藏、边水油藏直井与水平井开发5 a 后的累计产油量(针对目前模型大小,选取5 a 开发时间能够反映水平井径向流、线性流及拟径向流),最后将水平井累计产油量与直井累计产油量相除,获得水平井—直井产能比(表1)。从计算结果可知,在所给因素取值范围内,边水油藏的水平井—直井产能比取值为2.13~9.12,最大与最小产能比的差为6.99;底水油藏水平井—直井产能比的取值为1.78~8.83,最大与最小产能比的差为7.05。因此,与边水油藏相比,底水油藏水平井—直井产能比对因素变化更加敏感。
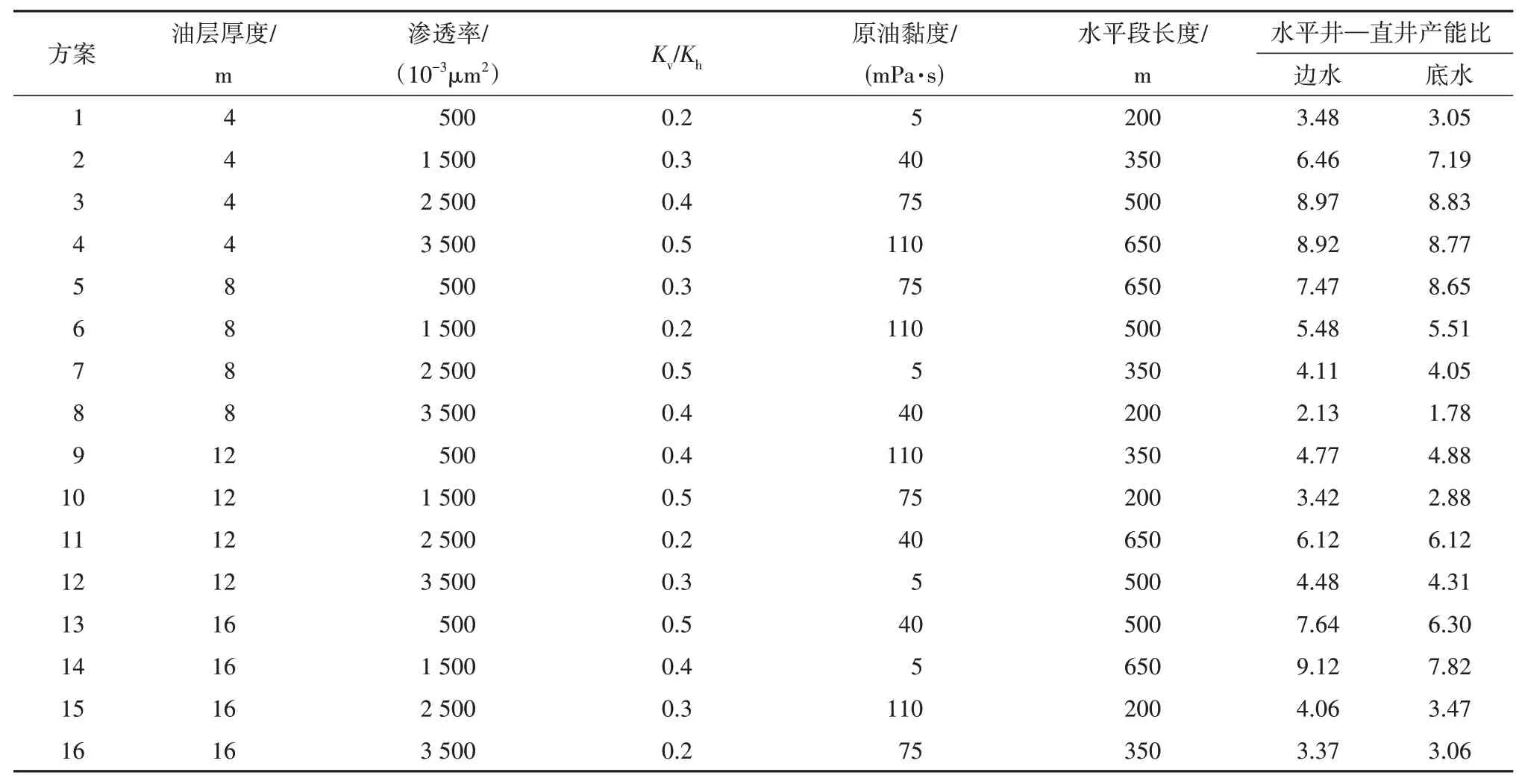
表1 各因素水平组合及相应的产能比Table 1 Factor level combinations and corresponding productivity ratios
1.2 等效井数折算比计算模型
运用获得的边、底水油藏的累计产油量影响因素与等效井数折算比(水平井—直井产能比)等数据,采用多元回归方法,可得到边水油藏、底水油藏的等效井数折算比计算模型。
边水油藏计算公式为
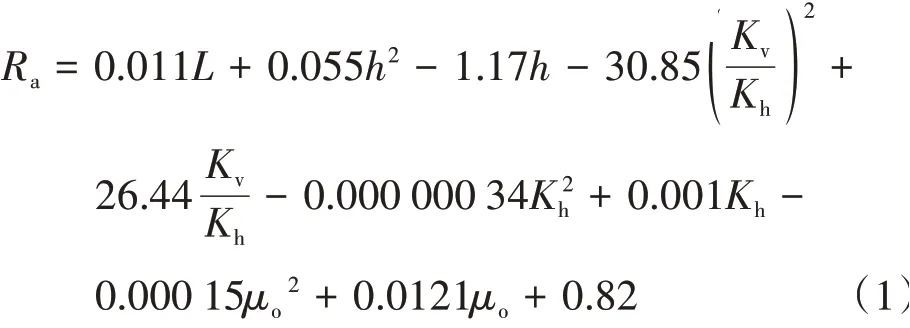
底水油藏计算公式为可

式中:Ra——边水油藏等效井数折算比;Rb——底水油藏等效井数折算比;h——油层厚度,m;Kv——垂向渗透率,10−3μm2;Kh——水平渗透率,10−3μm2;μo——原油黏度,mPa·s;L——水平井水平段长度,m。
由边水油藏、底水油藏的等效井数折算比计算模型计算的等效井数折算比,与数值模拟的计算结果相比较(图2)可知,边水油藏、底水油藏对比结果的散点均分布在x=y的直线附近(边水油藏与底水油藏的回归相关系数分别为0.959、0.972)。等效井数折算比计算模型计算的等效井数折算比,与数值模拟计算结果吻合度较高,能够满足矿场需求。
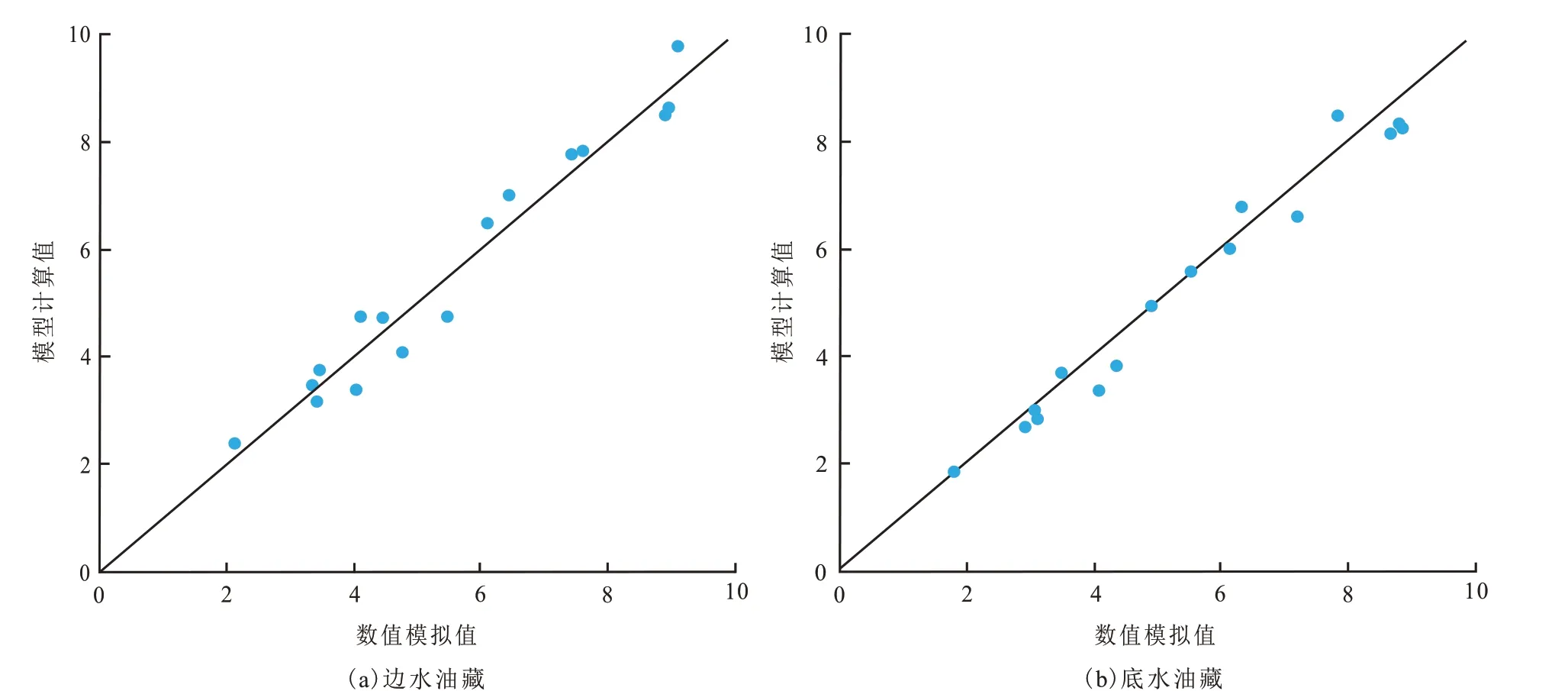
图2 等效井数折算比模型与数值模拟的计算结果关系Fig.2 Relations of calculation between conversion ratio calculation model for equivalent number of wells and numerical simulation
2 采收率预测模型及其影响因素
2.1 预测模型
根据南海东部已开发的56 个水驱砂岩油藏(28 个边水油藏和28 个底水油藏)的地质与生产资料,对影响油藏采收率的因素(含油面积、油层厚度、孔隙度、原始含油饱和度、渗透率、原油黏度及等效井网密度等)进行Pearson 相关性分析,分析结果见表2。其中,等效井网密度为单元储层面积的等效直井数,而等效直井数为水平井折算成直井后的总直井数。从表2 可知:边水油藏的含油面积、孔隙度、原始含油饱和度与采收率相关性弱(相关系数小于0.3),油层厚度、等效井网密度、原油黏度与采收率为相关性中等(相关系数为0.3~0.5),渗透率与采收率相关性强(相关系数大于0.5);底水油藏的含油面积、孔隙度、原始含油饱和度与采收率弱相关(相关系数小于0.3),原油黏度与采收率中度相关(相关系数为0.3~0.5),油层厚度、渗透率、等效井网密度与采收率强相关(相关系数大于0.5)。
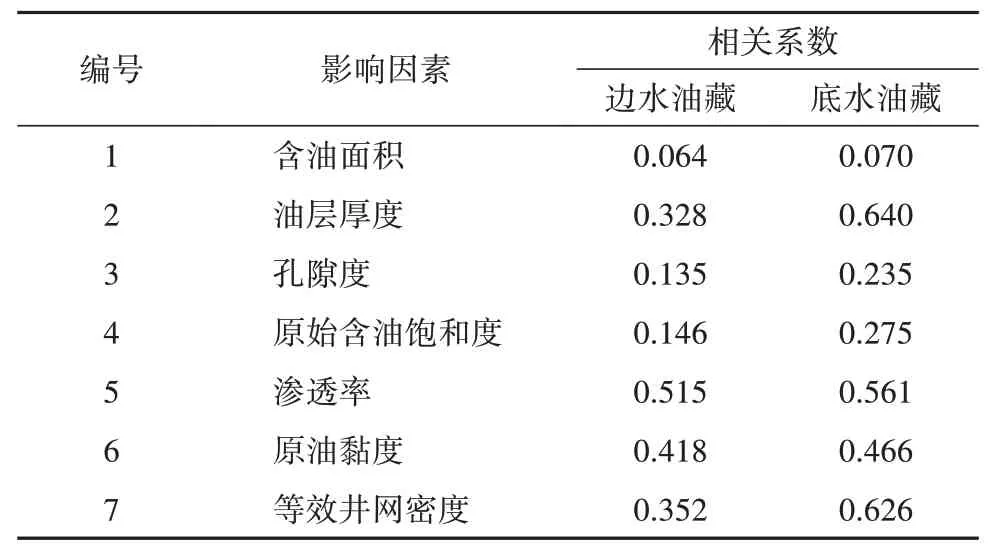
表2 采收率影响因素相关系数Table 2 Correlation coefficients of influencing factors of recovery factor
选取与采收率中—强相关的因素(油层厚度、渗透率、原油黏度和等效井网密度)作为南海东部边水油藏、底水油藏采收率回归的基础参数。通过南海东部水驱砂岩油藏开发资料,分析各因素对采收率影响,获得了油藏采收率与油层厚度(h)、流度对数等效井网密度的幂指数呈线性关系,因此多元回归的油藏采收率预测模型的形式可表示为
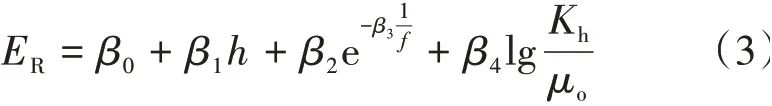
式中:ER——采收率,%;f——等效井网密度,口/km2;β0、β1、β2、β3、β4——回归系数。
基于以上关于等效井网密度的研究和南海东部砂岩油藏的实际资料,结合式(3),可获得边水油藏与底水油藏的采收率预测模型。
边水油藏采收率预测模型为
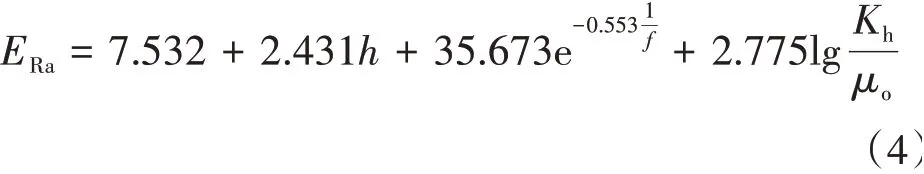
式中ERa——边水油藏采收率,%。
底水油藏采收率预测模型为
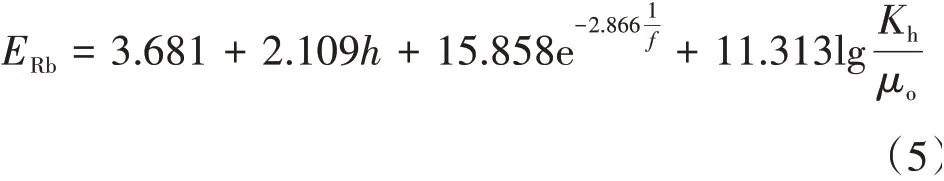
式中ERb——底水油藏采收率,%。
对比采收率预测模型计算结果与实际采收率可知(图3),边水油藏、底水油藏对比结果的散点均分布在x=y的直线附近(边水油藏与底水油藏的回归相关系数分别为0.918、0.926),采收率预测模型计算结果与实际结果吻合度较高。
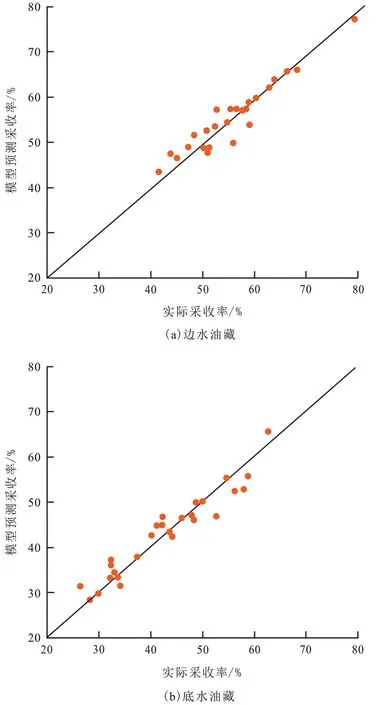
图3 预测模型计算与实际采收率对比Fig.3 Comparison of recovery calculated by prediction model with actual recovery
2.2 影响因素
根据建立的采收率预测模型,分析边水油藏、底水油藏在不同流度下采收率与井网密度的关系(图4)。
由图4 可知,当流度一定时,边水油藏、底水油藏的采收率随等效井网密度增加呈现出先增加快后增加慢的规律,当井网密度增加到3 口/km2后采收率增加幅度缓慢。
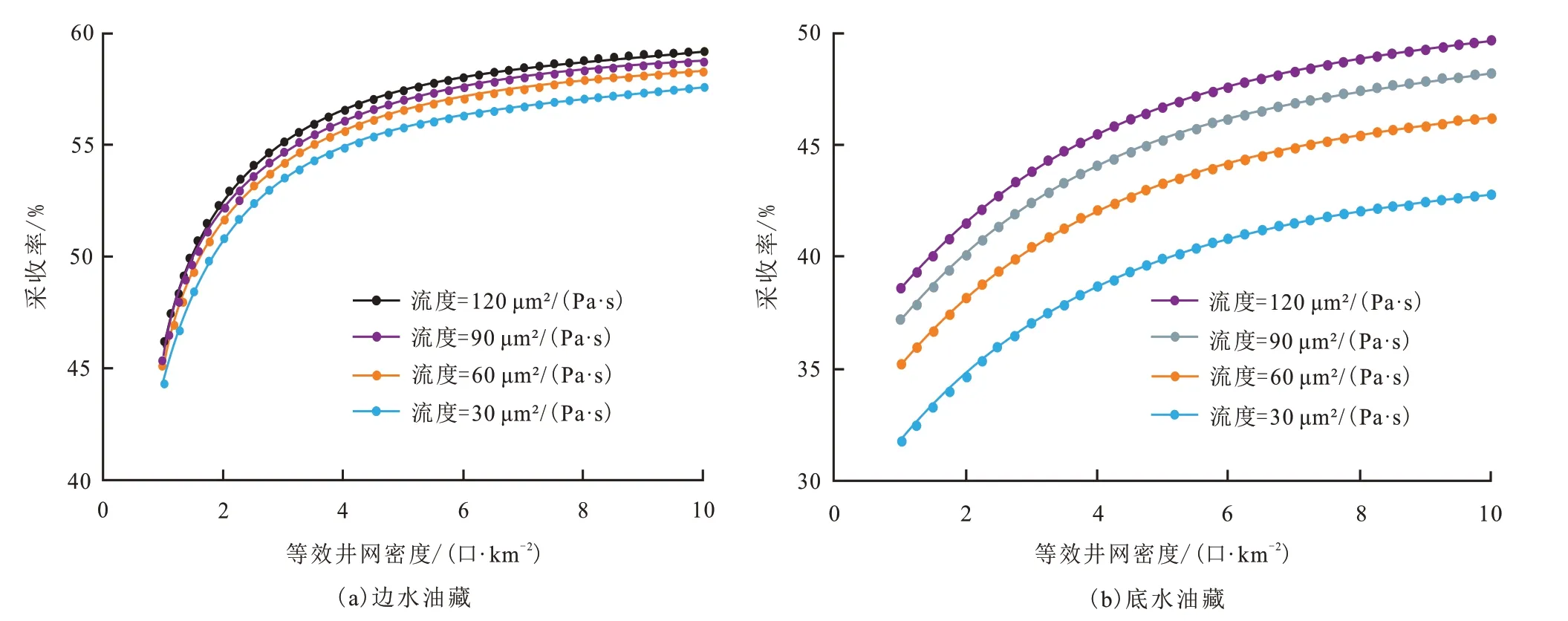
图4 不同流度下采收率与井网密度的关系Fig.4 Relations between recovery factor and well pattern density with different mobility
开发初期,由于井数少、井间距大、井间干扰小,其采收率随等效井网密度增加而快速增加(井网密度小于等于3 口/km2);随着开发的进行,井网密度增加(井网密度大于3 口/km2),井间干扰不能被忽略,故油藏采收率随等效井网密度增加而增加的趋势变缓。
当等效井网密度不变时,边水油藏、底水油藏的采收率随流度的增加而增加,且边水油藏采收率的增幅要小于底水油藏。对于底水油藏,流度增加可有效增加底水驱动波及体积;而对于边水油藏,流度增加对边水波及体积增加量影响相对较小,因此流度增加对边水油藏采收率的增幅小于底水油藏。
3 验证实例
为进一步验证等效井数折算比计算模型和采收率预测模型的准确性和适用性,选取样本以外8 个南海东部水驱砂岩油藏(4 个边水油藏,4 个底水油藏),分别将等效井数折算比计算模型的计算结果、采收率预测模型计算结果与其对应的实际结果进行对比(表3),实际等效井数折算比为水平井累计产油量的平均值与直井累计产油量平均值之比。对比结果表明,等效井数折算比计算模型的计算结果与实际值相对误差均在5%以内(边水油藏的最大相对误差为4.92%,底水油藏的最大相对误差为4.46%);采收率预测模型计算结果与实际采收率的相对误差均在5%以内(边水油藏的最大相对误差为4.73%,底水油藏的最大相对误差为4.48%)。
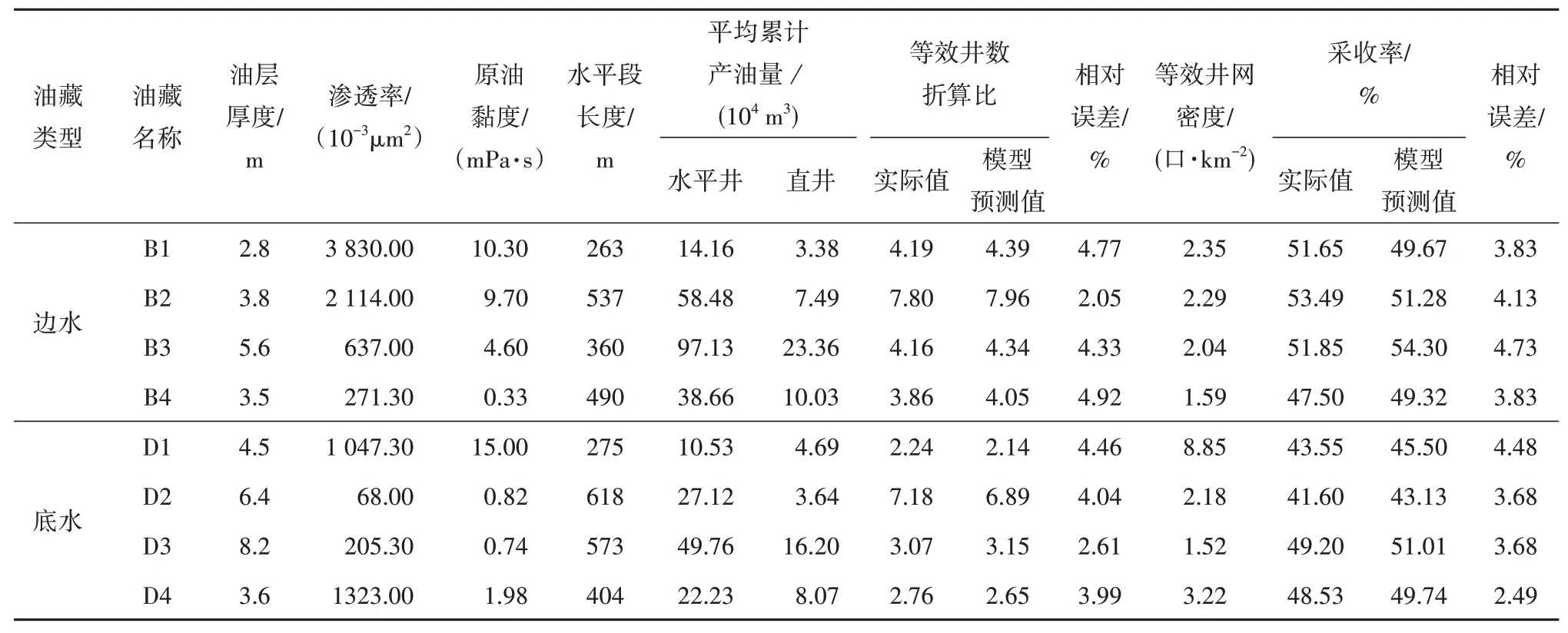
表3 等效井数折算比计算模型、采收率预测模型计算结果与实际值对比Table 3 Comparisons of calculation by conversion ratio calculation model for equivalent number of wells and recovery prediction model vs.actual values
从以上对比分析可知,建立的等效井数折算比计算模型能够准确地计算水平井等效为直井时的折算比,基于此建立的采收率预测模型能够准确地预测南海东部水驱砂岩油藏的采收率。
4 结 论
(1)建立了水平井与直井井数折算比计算模型,以此得到适用于南海东部水驱砂岩油藏的采收率预测模型,验证结果表明模型预测精度高。
(2)当流度一定时,随等效井网密度的增加,边水油藏、底水油藏的采收率呈现出先增加快、后增加慢的规律,当井网密度增加至3 口/km2后,采收率增加幅度减缓。
(3)当等效井网密度不变时,边水油藏、底水油藏的采收率随着流度的增加而增加,且边水油藏采收率的增幅要小于底水油藏。

