一种含自由曲面的离轴三反光学系统设计
项建胜,潘国庆,2,孟卫华,2
(1.中国空空导弹研究院,河南 洛阳 471009;2.航空制导武器航空科技重点实验室,河南 洛阳 471009)
1 引 言
离轴三反光学系统一般由三个离轴反射镜组成,通过合理设置三个反射镜的离轴量、倾斜量、间距、面型等参数,可以实现无遮挡无色差高质量的成像光学系统设计方案。离轴三反射镜光学系统由于采用纯反射元件因此无系统色差,在设计中将反射镜与安装结构采用同一材料,这样光学与机械结构有着相同的热膨胀系数,从理论上将系统无热差。因此离轴三反系统宽光谱成像仪、航天航空侦查观测方面有着广阔的应用前景[1]。
由于离轴三反光学系统为一非对称倾斜光学系统,采用传统设计手段很难达到较好的像差平衡。随着目前自由曲面光学在设计理论、加工检测等方面的发展,在光学系统设计中采用自由曲面面型已成为可能[2]。自由曲面的非旋转对称性为光学系统设计提供了更多的自由度,将其应用在离轴三反光学系统中可以极大地提升像差校正水平,使光学系统成像质量接近衍射极限。
2 离轴三反光学系统初始结构计算
离轴三反光学系统是从同轴三反光学系统中选取各个反射镜一定的离轴量与倾斜角而来的,其初始结构一般按照近轴光学计算同轴三反光学系统的三个反射镜的曲率半径、间隔、系统焦距等。一般而言,在初始结构计算中系统焦距、反射镜间隔、后截距等参数为输入量,根据这些输入量可以计算出三个反射镜的光焦度。同轴三反光学系统光路图如图1所示。

图1 同轴三反光学系统近轴光学示意图Fig.1 Thr paraxial zone of coaxial three-mirror optical system
记第一反射镜光焦度为φ1,第二反射镜光焦度为φ2,第三反射镜光焦度为φ3,系统焦距为f,t1为第一、二反射镜间距,t2第二、三反射镜间距,t3为系统后截距。h1、h2、h3分别为入射光线在第一、二、三反射镜的高度。
由图1中几何关系可知存在如下比例关系:
(1)
(2)
(3)
联立式(1)~(3)可以得出l3,则根据物像关系公式可以得出第三反射镜的光焦度φ3。
(4)
同理,按照上述方法可以得出第二反射镜的光焦度Φ2。
(5)
为了满足光学系统场曲为零,则光学系统Petzval之和为零,即∑φ=0,根据式(4)、(5)可知第二、三反射镜光焦度均可被第一反射镜光焦度表示。由此可以得出φ1[3]:
(6)
至此,在满足系统焦距与场曲为零的前提下,在给定反射镜间隔与后截距条件下,三个反射镜的光焦度可以完全由上述条件计算出来。本文光学系统系统焦距要求是250 mm,按照上述初始结构计算方法,设定不同间隔,可以计算出多组初始结构。根据上述方法计算出三种初始结构见表1。

表1 初始结构Tab.1 The orginal optical structure
为了减小光学系统空间占用,选用第三种初始结构(如图2所示)做为出发点,进行光学系统方案设计。
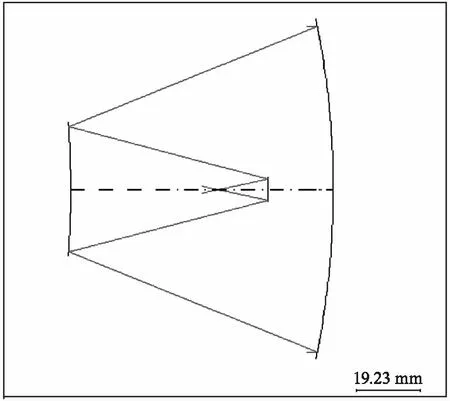
图2 同轴三反初始结构Fig.2 The original structure of coaxial three-mirror system
3 离轴三反光学系统设计思路
光学系统主要设计要求如表2所示。

表2 光学系统设计要求Tab.2 The parament of optical system
光学系统主要设计思路为:根据初始结构建立模型,由于初始结构是根据近轴光学计算而来的,能够满足系统外形结构与焦距、口径要求,对系统初级像差并无校正,因此初始结构存在较多的初级像差。
以校正初级像差为出发点,在同轴三反的基础上保持初始结构中三个反射镜的曲率半径与间隔不变,设置反射镜面型为二次曲面,主要对系统球差、彗差与像散进行校正。
在优化完成的同轴三反的基础上,根据离轴三反的外形结构形式,设置三个反射镜初始的倾斜角度与离轴量,将倾斜角、离轴量、曲率半径、面型参数做为自变量进行优化设计,检查系统像差校正情况。根据像差校正情况,选择一个反射镜面型采用自由曲面进行优化设计。自由曲面有多种表示方式,本文选用Zernike多项式表达方法。Zernike多项式在拟合光学表面、波前差或光学干涉数据等方面有着广泛的应用。Zernike多项式中子项是正交各自独立的,且分别对应着不同的光学像差,在定量描述像差方面有着天然的优势。根据像差残留情况,选择Zerniek多项式中的残留像差对应项做为自变量参与系统优化,如此循环直至像差得到较好的校正[4]。整个光学系统设计流程如图3所示。
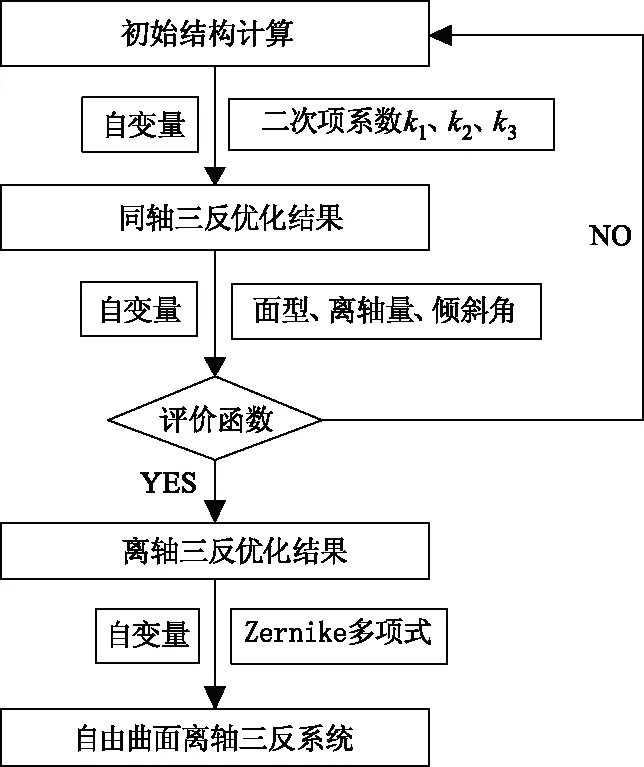
图3 含自由曲面离轴三反光学系统设计流程Fig.3 The design flow of off-axis three-mirror system with freeform
4 离轴三反光学系统设计过程
在光学系统优化过程中主要约束条件是系统焦距、外形尺寸、反射镜安装要求等。优化函数主要以系统波像差为目标,自变量主要为面型参数、离轴量、倾斜角、自由曲面多项式等。
光学系统按照图3设计流程进行优化设计,同轴三反光学系统优化设计结果如图4所示。系统像差如图5所示。可以看出同轴三反光学系统在初始结构的基础上,通过引入二次曲面面型,系统初级像差如三级球差、彗差校正较好,但还残余一些高级像差。由于这是同轴系统,视场较小因此像散不是主要像差。

图4 同轴三反优化结果Fig.4 Optimization of coaxial three-mirror system

图5 像差曲线图Fig.5 Ray aberration curves
在同轴三反光学系统方案基础上设置三个反射镜的离轴量、倾斜角,进行离轴三反光学系统设计。光学系统设计结果见图6、7、8。三个反射镜均采用高次非球面面型,全视场弥散斑大小见表3。通过像差分析来看,系统还残留一定的高级球差与彗差。

表3 全视场弥散斑分布大小Tab.3 FFD of spot

图6 离轴三反光学系统Fig.6 Off-axis three-mirror optical system

图7 全视场内弥散斑大小Fig.7 FFD of spot

图8 畸变图Fig.8 The distoration
5 含自由曲面的离轴三反光学系统设计结果
在上述离轴三反光学系统设计基础上,针对残留像差分布情况,选择Zernike自由曲面中球差与彗差对应项(主要是第8、9、13项)做为自变量继续优化设计,得出最终光学系统方案。光学系统如图9所示。其中第一反射镜为高次非球面面型,第二反射镜为自由曲面面型,第三反射镜为高次非球面面型。自由曲面参与优化后,系统整体像差得到了较好地校正,全视场内弥散斑大小见表4。可以看出系统弥散斑大小相比于之前得到了较大程度的下降。全视场弥散斑分布图见图10。系统畸变控制较好,见图11。系统成像质量接近衍射极限,光学系统传递函数见图12。

图9 自由曲面离轴三反光学系统图Fig.9 Off-axis three-mirror system with freeform optics
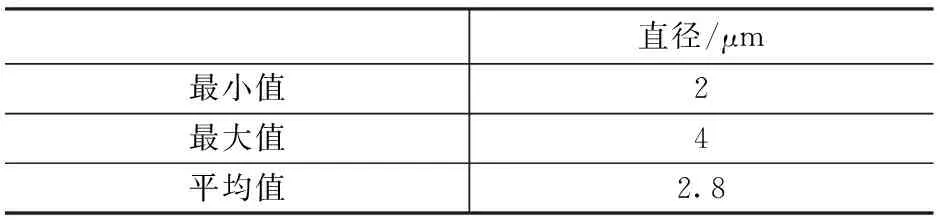
表4 全视场内弥散斑大小Tab.4 FFD of spot

图10 全视场弥散斑图Fig.10 FFD of spot

图11 畸变图Fig.11 The distoration

图12 MTFFig.12 MTF
含自由曲面离轴三反光学系统光学结构参数如表5所示。

表5 光学结构参数Tab.5 The final optical structure parament
6 结 论
设计了一种含自由曲面离轴三反光学系统,以近轴几何光学计算同轴三反光学系统的初始结构,在此初始结构基础上经过优化设计得出传统意义上的离轴三反光学系统方案。在此基础上选取第二反射镜采用Zernike自由曲面结构,根据光学系统的像差分布情况,选取对应项为自变量参与优化设计,大大提高了光学系统的像差校正水平,使成像质量接近衍射极限水平。
离轴三反光学系统由于是一种非对称性结构,特别是在引入自由曲面后,由于自由曲面的非旋转对称性,在提供设计自由度的同时也引入了系统复杂度,基于同轴的像差理论不适应描述含自由曲面的离轴三反光学系统,而且在优化设计结构边界条件也更加复杂,这些问题均需要大力发展非对称性像差平衡理论来解决。因此含自由曲面光学系统的像差平衡理论应是今后光学设计重点研究的方向之一[5]。

