基于多波长光学系统结构的透射波前检测

朱大勇,张齐元,王 芳,朱怀康,贾文昕,韩 森,

(1.上海理工大学光电信息与计算机工程学院,上海 200093；2.苏州慧利仪器有限责任公司,江苏 苏州 215123；3.苏州科技大学物理科学与技术学院,江苏 苏州 215009)

1 引 言

波前像差是光学系统中重要的性能评价指标,传统波前检测技术只能检测有限特定波长的透射波前[1-2]。为了解决透射波前检测受波长限制的问题,提出了多波长透射波前检测技术,即使用少数几个波长透射波前的测量数据,通过透射波前与波长的函数关系计算出一定波段范围内任意波长透射波前[3-5],其中波前使用Zernike多项式表示[6]。为了验证多波长波前检测技术,以一个常规的632.8nm激光干涉仪为原型,采用更换激光光源的方式设计不同波长激光干涉仪[7]。通过测量光学透镜(镜头)在不同波长下的Zernike系数,初步验证了透射波前Zernike系数与波长的函数关系以及多波长波前检测的可行性[7]。由于在检测中不可避免地存在系统误差和测量误差,因此进一步分析了系统误差和测量误差对预测波前Zernike系数的影响,并改进拟合Zernike系数-波长曲线的方法以进一步提高计算精度[8]。相关实验结果表明了新的检测技术能够为光学系统(镜头)的性能检测提供更加完善的方案[8]。

目前激光干涉技术仍是高精度测量光学系统波前像差最主要的方式,其中菲索干涉仪以其共光路、抗干扰能力强等特点成为了主流商业激光干涉仪[9-10]。但现阶段产品中菲索干涉仪均为单波长激光干涉仪,而在多波长波前技术中需要使用到几种不同波长激光干涉仪,显然在检测中同时使用多个激光干涉仪对一个样品进行测量是不合理的,也是不经济的(多种激光干涉仪中不同大小的系统误差会引入到测量结果中)。虽然在实验中可以通过更换光源的方式配置不同波长激光干涉仪,但该方法不宜在实际中使用[7]。另外,以往的实验结果虽然基本符合预期,但整体来说实验仍然有很多需要改进的地方,其中主要的问题有以下几个方面,第一,实验中使用的光源的波长范围是532～1064 nm,通过仿真可知大部分系统在整个可见光到近红外这个波段范围内,短波部分(特别是近紫外)数据相较于其他波段变化更大,因此增加短波光源将有助于在VNIR(400～1000 nm)波段更精确地预测曲线；第二,实验过程中测量不同波长透射波前时都需要不同波长的光源,每次更换光源需要一定时间进行调整,导致测量一个样品的时间较长,检测效率较低；第三,由于干涉仪机械结构的限制,在实验中更换光源后如果重新调整干涉仪的准直物镜会产生较大的系统误差,而在不调整准直系统的情况下测量结果中又会引入干涉仪光学系统自身的色差；最后,非常重要的一点是实验中使用的装置并不是完整的仪器,不利于多波长波前检测技术的普及与推广。针对上述问题,本文设计了多波长激光干涉仪光学结构,为后续多波长激光干涉仪的研发以及多波长波前检测技术实现工程化打下良好的基础。

2 结构及装调

2.1 多波长激光干涉仪基本光学结构

多波长激光干涉仪与常规激光干涉仪最大的区别在于光源的数量,因此需要重点考虑如何在一个干涉系统中集成多个波长激光光源。多波长激光干涉仪以菲索干涉仪为原型进行改进,其结构如图1所示,虚线框内为菲索干涉仪的基本结构,使用分光棱镜将不同波长的光折转到干涉仪的光路中。在测量的过程中需要保证从菲索干涉仪出射的光为平行光,由于准直系统自身的色差,当波长改变时出射光束的准直度会发生改变[11-12]。为了得到准确的测量结果,在多波长激光干涉仪中需要保证准直系统可以沿光轴方向移动,使出射光束始终为准直度较好的平行光。此外根据研究,相比于测试波长的数量,测试波长所在波段的位置对于预测Zernike系数-波长曲线的准确性更加重要[8],因此在原有实验装置的光源基础上增加了473 nm激光,同时为了控制光学结构的尺寸,选用532 nm、632.8 nm、721 nm和1064 nm激光作为共同光源。这样仪器在测量透射波前时仅需打开相应的光源,并调整准直透镜的距离就能配置出不同波长的干涉测试光路。

图1 多波长激光干涉仪原理结构图Fig.1 Schematic diagram of multi-wavelength laser interferometer

该光学结构选用口径为3/4 in(19.05 mm)的标准镜作为参考镜,因此准直系统的口径应大于19 mm。为了快速对该光学结构进行实验验证,尽可能选购市场上现有的光学元件进行组合。准直系统选择口径为25 mm、焦距为150 mm的镜头。传感器选用对应的CCD,干涉图要完全成像在CCD的有效感光面积内,根据准直镜头的参数,成像系统选择口径为12.7 mm、焦距为25 mm的镜头。

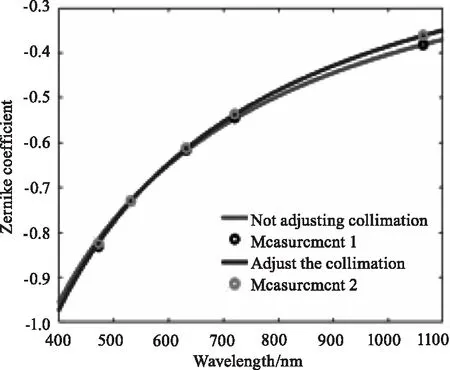
在干涉测量中参考光束的准直度会对测量结果产生一定的影响,文献[8]分析了当准直系统为单色系统时在多波长波前测量中,不调整光束准直度对测量结果的影响。仿真结果显示当更换波长后不调整准直系统相比于调整准直系统,Z6和Z7的数值会出现较大的偏差,而Z4、Z5和Z8的数值则不会产生较大的变化(通常在实际检测中仅分析Z4～Z8),但调不调整准直系统不会改变被测光学系统波前Zernike系数-波长曲线的函数关系。由于之前实验装置的限制,在以往的实验中仅验证了被测系统在不调整准直系统的情况下的测量结果,虽然预测出的Zernike系数-波长曲线也符合Conrady公式的函数关系,但实际上得到的是被测系统引入干涉系统色差后的数值[4-7]。为此多波长激光干涉仪光学结构重要改进之一是能够在测量过程中调整光束的准直度,但为了尽可能减小调整准直系统所带来的光轴偏移误差,准直系统采用了双胶合镜头。相比于常规干涉仪使用的单色系统,消色差系统可以通过不同材料的组合去消除两个边缘光的色差,使其焦点随波长变化的距离大大的缩短。图2为选购双胶合镜头在473～1064 nm波段范围的位置色差曲线,其焦点的位移距离为1.1 mm,而相同参数的单色系统则为5 mm左右。

图2 双胶合准直镜头的色焦移图Fig.2 Color focus shift of a double gluing in collimating system lens

由于干涉图像是相干成像,理论上改变波长后不调整成像系统的焦点位置对测试结果的影响很小[13],主要会使干涉图的边缘发生模糊,在以往的实验中为了验证Zernike系数与波长的函数关系,通常使用较小口径的掩膜去掉较大范围的边缘图像[4-7]。而为了减小系统的调整误差(调整准直系统产生光轴偏移一样类型的误差),新仪器在测量过程中仍然不调整成像系统,同时为了减小干涉图边缘模糊的现象,成像系统也采用了消色差系统。由于成像系统的焦距较短,并且校正了色差,所以即使在测量过程中不调整成像系统,干涉图的边缘也能保证比较清晰,这样就可以使用较大口径的掩膜来测量透射波前。

2.2 多波长激光干涉仪的装调

多波长激光干涉仪光学结构按照系统组成分别对各部分进行装调。调节分光棱镜时,把5个分光棱镜用笼式系统(同轴系统)连接起来。如图3所示,棱镜安装座底部和支架支杆连接,使用支杆初步调节5个分光棱镜高度,再利用激光器调整好棱镜系统的位置。

图3 使用笼式系统安装5个分光棱镜Fig.3 Five optical splitting prisms in a cage system

安装激光器时,由于激光经过分光棱镜后光强会发生衰减,因此先安装最左端的He-Ne激光器(实际验证经过最大衰减之后的激光仍然不影响测量),同时在笼式系统最右侧棱镜后面加装显微物镜作为点光源生成器。如图4所示,为了更加方便快捷地调节激光器,在棱镜安装座及同轴系统放置对准板。调节最左侧的激光器,使得激光光线同时穿过各个对准板中心,并保证从显微物镜出射的光斑是清晰的、均匀的,此时把激光器进行固定。

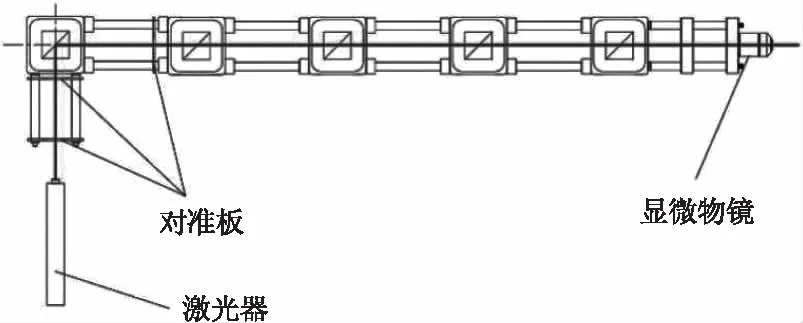
图4 最左侧激光器装调示意图Fig.4 The leftmost laser installation diagram

按照相同的方法安装并调节中间三个激光器,从左到右波长分别是532 nm、473 nm、721 nm。安装最右侧1064 nm的激光器时,由于1064 nm激光是不可见的,所以将对准板换为荧光对准板。在实际调试1064 nm激光器时通过红外观察仪就能够在荧光对准板上更加清楚的看到出射的光点,这样就可以按照和可见光相同的方式进行安装。

图5 分光棱镜和各激光器示意图及荧光对准板实物图Fig.5 Schematic diagram of dispersion prism and schematic diagram and the laser fluorescence alignment plate

安装多波长激光干涉仪的主体部分时,将准直镜头、分光镜、可变光阑以及成像镜头都安装于笼式系统内,以尽可能保证它们同轴。如图6所示,在分光镜与准直镜头之间放置两块对准板,调整干涉仪主体的笼式系统使激光穿过两块对准板靶心,以此来保证光源的笼式系统与其相互垂直。准直镜头安装于调节范围为2 mm的Z轴平移安装座内,可以满足波长从473～1064 nm的过程中准直镜头沿光轴方向移动的范围。此外,从图2的色焦位移曲线可以看出,准直镜头在532 nm时的后截距最短,因此使用Z轴平移安装座将准直镜头旋至安装座的接近最内侧的位置(靠近薄膜分光镜方向)。以532 nm激光作为基准,使用剪切干涉仪观测出射光束的准直度。调整Z轴平移安装座,在光束准直度最好的位置将其固定在同轴系统上。这样更换其他波长时只需旋转Z轴平移安装座的旋钮,并根据剪切干涉仪来调整准直镜头即可。

图6 整体结构示意图Fig.6 The overall structure diagram

在多波长激光干涉仪光学结构中安装相移模块(PZT)、CCD以及标准镜后,调节光阑位置至准直系统的焦点处并固定,再调整成像系统的位置,当从成像系统出射的光线几乎是准直光时将其固定(成像系统的焦点也在光阑位置)。CCD底部的支杆安装在Z轴位移台上,在测量不同距离的光学元件(或光学系统)时,通过调整CCD的位置使干涉图清晰。最终的该光学结构实物图如图7所示,配合五维支架和平行导轨形成了一套完整的多波长激光干涉测量装置。此多波长激光干涉测量装置可用于反射和透射等多种干涉检测,本文将进行透射波前的检测,从而进一步判断该结构的性能状态。

图7 多波长激光干涉仪光学结构实物图Fig.7 Optical structure of multi-wavelength laser interferometer

3 实测结果及分析

3.1 测量结果

为了验证多波长激光干涉测量装置的实际效果,使用该光学结构配置出来的多波长激光干涉仪对光学镜头进行检测,并且分别在该多波长激光干涉仪调整准直系统和不调整准直系统(以532 nm为基准)两种情况下进行,以便对比干涉仪准直系统色差对测量结果的影响。使用该多波长激光干涉仪测量双胶合镜头,测量结果如表1和表2所示。

表1 双胶合镜头在调整准直系统下 测量的Zernike系数Tab.1 The Zernike parameters of double gluing lens in collimating system with adjusting

表2 双胶合镜头在不调整准直系统下 测量的Zernike系数Tab.2 The Zernike parameters of double gluing lens in collimating system without adjusting

被测系统(使用Zemax仿真)的Zernike系数-波长曲线可以使用Conrady公式表示,仿真时使用求解的方式即可得到Zernike系数-波长曲线[4-7]。由于实测结果存在测量误差、系统误差和随机误差等多种误差,而求解Conrady公式得到的结果是唯一的(3个方程求解3个未知数),这就意味着如果测量结果中出现较大的误差,则会直接影响预测曲线的趋势。在实际中为了减小误差的影响,可以使用拟合的方式预测曲线,但直接拟合Conrady公式只能得到单调曲线,因此课题组发展了转换多项式的方法拟合曲线,计算具体流程图如图8所示[8]。

图8 转换多项式法计算Zernike系数-波长曲线示意图Fig.8 The transformation polynomial method is used to calculate the Zernike coefficient-wavelength curve

该方法的本质是将Conrady公式转换为多项式的形式,将Conrady公式左右两边均乘以λn(其中n≥3.5)得到新的公式,通过数学工具拟合新公式得到系数Ai、Bi、Ci,再将Ai、Bi、Ci带回到原Conrady公式并绘制Zernike系数-波长曲线。由于多项式公式在数学中具有通用性,这样拟合的结果更加准确,最终得到的曲线可以是单调曲线也可以是带一个拐点的曲线。图9和图10分别为调整准直系统和不调整准直系统情况下使用转换多项式法预测的Zernike系数-波长曲线。从图9和图10可以看出,利用Conrady公式转换多项式的方法来拟合Zernike系数-波长曲线可以得到比较准确的预测曲线。对于预测曲线的准确性来说,除了采用科学的拟合方法之外,就是要依靠所设计多波长激光干涉仪实验装置的稳定性,这样才能保证测量数据的准确性与稳定性。

(a) Z4

(b) Z5

(c) Z6

(d) Z7

(e) Z8图9 调整准直系统双胶合透镜Zernike系数-波长曲线Fig.9 The Zernike coefficient - wavelength curve of the collimating system′s double gluing lens with adjusting

(a) Z4

(b) Z5

(c) Z6

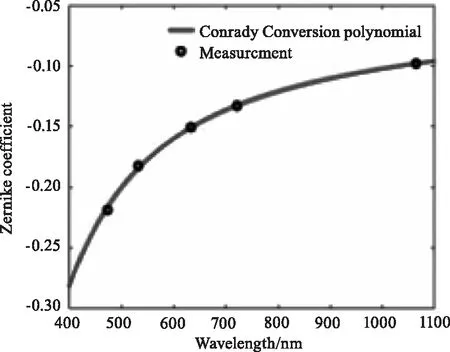
(d) Z7

(e) Z8图10 不调整准直系统双胶合透镜Zernike系数-波长曲线Fig.10 The Zernike coefficient - wavelength curve of the collimating system′s double gluing lens without adjusted

3.2 结果分析

图11为调整准直系统和不调整准直系统情况下使用转换多项式法预测的Zernike系数-波长对比曲线。从图中可以看出每一组的对比曲线都有不同程度的偏差,其中Z6、Z7和Z8偏差较为明显,这样的结果表明参考光束准直度会影响测量结果,而且预测曲线相差较大的区域主要是短波以及长波波段,从测量数据上看可以得知,当被测透镜的测量数据非常小时,拟合出的对比曲线在长波段会显得差别很大,而从实际的数值上来看两者差距并不是很大(比如Z8)。

(a) Z4

(b) Z5

(c) Z6

(d) Z7

(e) Z8图11 调准与不调整准直系统双胶合透镜Zernike 系数-波长曲线对比Fig.11 Comparison of Zernike coefficient-wavelength curves of collimating systems′ double gluing lens with and without adjusting

同时,由于准直系统自身存在着偏心误差,在调整准直系统之后不可能保证干涉仪光学系统的光轴不发生一点改变(相当于改变了测试仪器),同样会导致Z4～Z8产生较大的测量误差,因此拟合曲线也会产生明显的偏差。

在进行不调整准直系统实验时是以532 nm的准直度为基准进行实验测量,所以从图11也可以看出,532 nm所对应的调整准直系统与不调整准直系统的测量点是重合的,而实际上是对532 nm激光进行了重复测量,从表1和表2可以看出,两次实验测量532 nm的数据几乎相等,这也说明所设计的多波长激光干涉仪实验装置比较稳定。用实验数据来拟合Zernike系数-波长曲线时会发现有个别测试点拟合不太好的情况,这是因为实验过程中存在的各种误差导致测试数据不准确进而使得拟合曲线出现偏差。除了上述的各种误差外,在实验时光路调整的误差也会使得实验数据不准确,甚至会导致拟合曲线的趋势发生改变。同时,由于实验时判断参考光束的准直度是用眼睛直接观察剪切干涉仪条纹的方式,那么这个过程就存在一定的主观性,从而会使实验数据出现一定的偏差。所以,在之后的课题研究中需要对存在的问题做进一步的解决和完善。

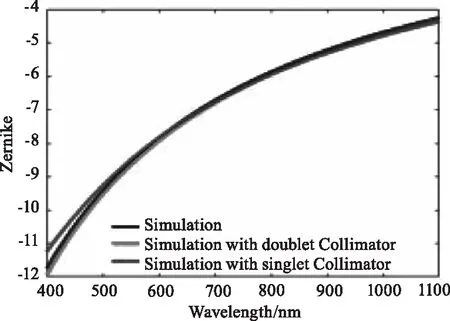
为了更加直观地对比说明被测双胶合镜头理论数据与实验数据的差别,于是对被测双胶合镜头进行模拟仿真。仿真系统中被测镜头在X和Y方向分别倾斜5 °,其中不仅模拟了实验时所使用的消色差双胶合透镜作为准直系统,还模拟了单透镜作为准直系统的情况,仿真结果如图12所示。

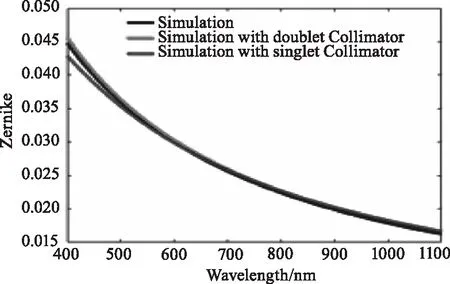
(a) Z4

(b) Z5

(c) Z6

(d) Z7

(e) Z8图12 双胶合透镜仿真对比曲线Fig.12 Double gluing lens simulation curves

观察图11和图12可知,实验数据拟合的曲线趋势正确但是和理论仿真还是有一定的差别,造成这种差别的原因就是之前所分析的各种实验误差以及被测镜头本身的性质,而且在实验中被测镜头的倾斜角度是未知的,软件仿真也不可能完全模拟出现实的实验设备与实验状态。同时也可以看出,单透镜作为准直系统和双胶合透镜作为准直系统之间的差别比较明显,结果表明,双胶合透镜作为准直系统时仿真结果更加接近理论数据,所以这是实验装置中选取消色差双胶合透镜作为准直系统的重要原因。

4 结 论

基于菲索干涉原理,设计了多波长激光干涉仪光学结构,在测量过程中只要切换激光光源,就能够快速完成不同波长干涉光路的配置,大大提高了多波长透射波前的检测效率。通过实验也证明了干涉仪准直系统的色差对测量结果有一定的影响,所以在实际测量中需要调整准直系统才能得到更准确的测量结果。尽管所有的部件都安装在笼式系统中,在调整的过程中仍然不可避免地产生光轴偏移误差,采购的双胶合镜头只在可见光波段内进行消色差,导致在473～1064 nm波段范围内色焦移仍然较大,并且虽然多波长激光干涉仪简化了更换光源的步骤,但更换光源后仍然需要根据剪切干涉仪调准准直系统,尤其在1064 nm波长时,需要配合红外观测仪才能使用。因此后续可以采用对473 nm和1064 nm进行消色差设计,在进一步缩短色焦移范围的同时,可以使1064 nm与可见光聚焦在同一位置,便于在1064 nm时调整准直系统。此外多波长激光干涉仪在自动化控制等很多方面仍有较大的提升空间,本文对多波长激光干涉仪的探索,对多波长波前检测技术的推广及新仪器的研发都有积极意义。