延时间隔对爆破破岩的影响机制及应用研究

张西良 仪海豹 韩 寒 李二宝 汪 禹 杨海涛 周 健

(1.金属矿山安全与健康国家重点实验室,安徽 马鞍山 243000;2.中钢集团马鞍山矿山研究总院股份有限公司,安徽 马鞍山 243000;3.安徽省公安厅,安徽 合肥 230061;4.华唯金属矿产资源高效循环利用国家工程研究中心有限公司,安徽 马鞍山 243000;5.中南大学资源与安全工程学院,湖南 长沙 410083)

微差起爆是通过调整炮孔起爆延时间隔以降低爆破振动强度的重要技术手段，在矿山工程、岩土工程等爆破开挖领域得到了广泛的推广应用[1-3]。近年来，在微差减震方面诸多学者开展了大量研究工作[4-8]，成果丰硕。陈建龙等[4]结合毫秒延时起爆的控制基频和多普勒效应，实现了爆破频率和振动的主动控制;赵凯等[5]研究发现，毫秒延时爆破可以有效降低地表峰值振动速度，改变地表振动的频谱特性;张亮等[6]提出采用改进的CEEMDAN算法准确识别微差爆破延期时间，可以有效克服模态混叠现象;邱贤阳等[7]从HHT能量谱角度探究了短微差爆破的降振效果，分析了段数、相邻振幅比和最大段药量位置对降振效果的影响;冷振东等[8]研究了自由面对边坡爆破峰值振动速度的影响，指出同一排第一段爆破的振动速度大于后续段爆破。

已有研究成果主要从爆破振动能量分析、振动波形识别、应力波干扰减振等角度寻求适宜的微差时间，以降低爆破振动次生危害，而不同延时间隔对破岩量影响方面的研究有待深入。为此，本研究采用数值模拟方法对比分析延时间隔对破岩量的贡献机制，优选适宜的延时间隔，并通过现场试验进行可行性验证，为采场雷管段别选择及高效爆破提供指导。

1 数值计算方案及模型构建

1.1 数值计算方案

炸药爆炸是一个瞬时的高温、高压动态过程，难以依靠理论分析和数学公式计算爆破破岩范围来指导生产。LS-DYNA是通用的结构分析非线性有限元程序，在处理材料失效与大变形问题方面具有突出优势，可以模拟研究爆炸动荷载破岩过程[9-10]。为此，本研究采用LS-DYNA数值分析软件，分析起爆方式与延时间隔对爆破破岩的影响规律，寻求最佳的起爆延时间隔，指导现场生产爆破雷管起爆时间优选，为现场规模爆破试验提供理论依据。

考虑到计算机配置条件和数值计算能力，在不影响研究结果的前提下，分别采用准二维和三维数值计算模型进行分析。分析方案如下:

(1)准二维模型。采用3孔无荷载方案，其中前排2孔、后排1孔;二者之间分别设置延时间隔5、10、15、20、25、30、35、40、45、50 ms，对比分析不同延时下前排先起爆与后排先起爆的破岩效果。

(2)三维模型。采用5孔高应力荷载方案，其中中间1个孔、外围对称布置4个孔;中间孔先起爆，周边4个孔后起爆，两者之间分别设置延时间隔10、15、20、25、30、40、50 ms，研究不同延时对爆破破岩的影响。

1.2 数值模型构建

1.2.1 模型状态方程

本研究岩体采用LS-DYNA软件自带的弹塑性本构模型，炸药本构模型使用JWL状态方程模拟炸药爆轰过程[11-13]，方程式为

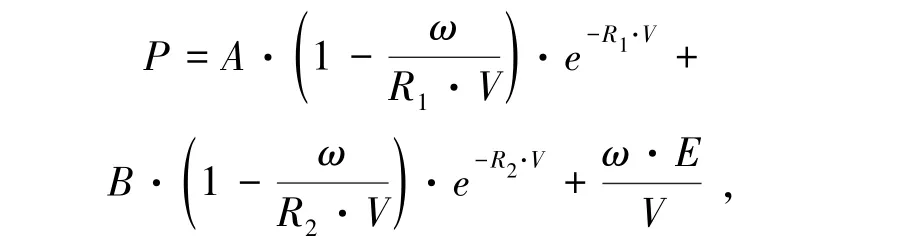
式中，P为压力，MPa;A、B、R1、R2、ω为爆轰参数;V为相对体积;E为初始比内能，J/m3。

JWL状态方程参数取值见表1，岩体物理力学参数取值见表2。空气采用NULL材料模型，定义沙漏系数控制爆炸过程能量的传递和转换。

表1 JWL状态方程参数Table 1 Parameters of the JWL state equation

表2 岩体物理力学参数Table 2 Physical and mechanical parameters of rock mass

1.2.2 模型尺寸参数

(1)准二维模型。模型尺寸为20 m×8 m(长度×宽度)。孔径76 mm，前排孔抵抗线0.8 m，孔距2 m，排距1.6 m。

(2)三维计算模型。模型尺寸为8 m×6 m×6 m(长度×宽度×高度)。孔径76 mm，前排孔抵抗线1.5 m，孔距2 m，排距1.6 m。

1.2.3 网格划分

根据炮孔尺寸及计算需要精细化划分计算网格。准二维模型中361 262个单元体，三维计算模型中781 494个单元体。

1.2.4 边界条件设置

准二维模型上侧为爆破自由面，三维模型上侧和侧面为自由面，其他边界上设置无反射条件，消除边界条件对计算结果的影响。

2 二维模型下延时间隔对破岩的影响分析

2.1 爆炸破岩过程分析

2.1.1 方案1(前排孔先起爆、后排孔后起爆)

方案1不同时刻的爆破应力云图如图1所示。

由图1分析可知，从时间上来看，炸药爆炸的破岩过程可以分为如下两个阶段:

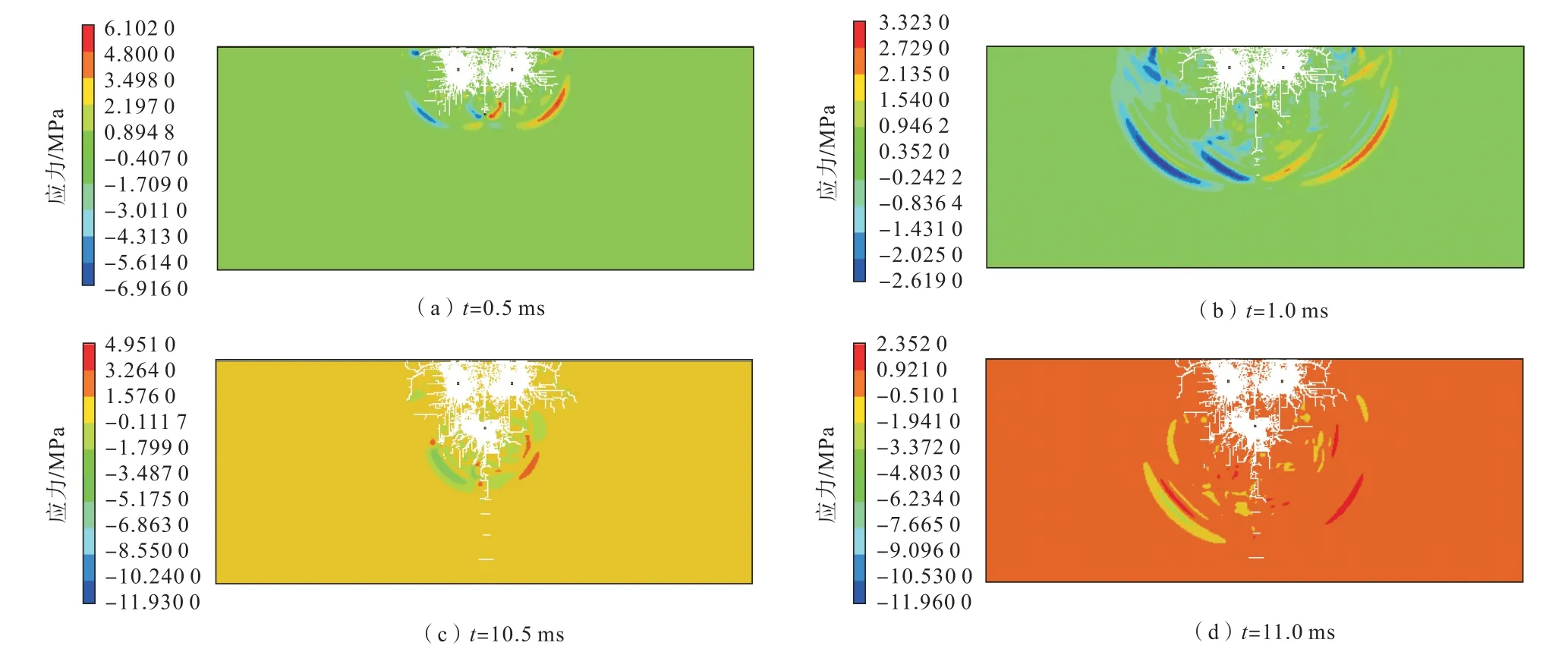
图1 方案1延时10 ms的爆破应力云图Fig.1 Blasting stress nephogram of scheme 1 with a delay of 10 ms

(1)第1阶段。前排孔起爆阶段。前排两个炮孔同时起爆后，爆炸应力波从炮孔中心位置以圆形逐渐向外扩展传播，且具有明显的对称性;在两个炮孔中心连线上形成明显的应力叠加现象。在爆炸冲击载荷的作用下，由爆心向外依次形成粉碎区和裂隙区。当应力波到达自由面时发生反射，由压缩应力波转变为拉伸应力波。在反射拉伸应力的作用下，岩石被拉断，发生片落[14-16]。随后，受高压爆生气体的影响，在拉伸应力和爆生气楔的双重作用下，径向初始裂隙迅速扩大。

(2)第2阶段。后排孔起爆阶段。前排孔爆破后创造了更好的自由面，为后排孔爆破创造了有利条件。后排炮孔起爆后，延续了第1阶段初始的破岩过程，在第1阶段的基础上再次形成新的破碎区域，引起岩石裂隙的扩展、崩落，最终完成了整个爆破破岩过程。

2.1.2 方案2(前排孔后起爆、后排孔先起爆)

方案2不同时刻的爆破应力云图如图2所示。

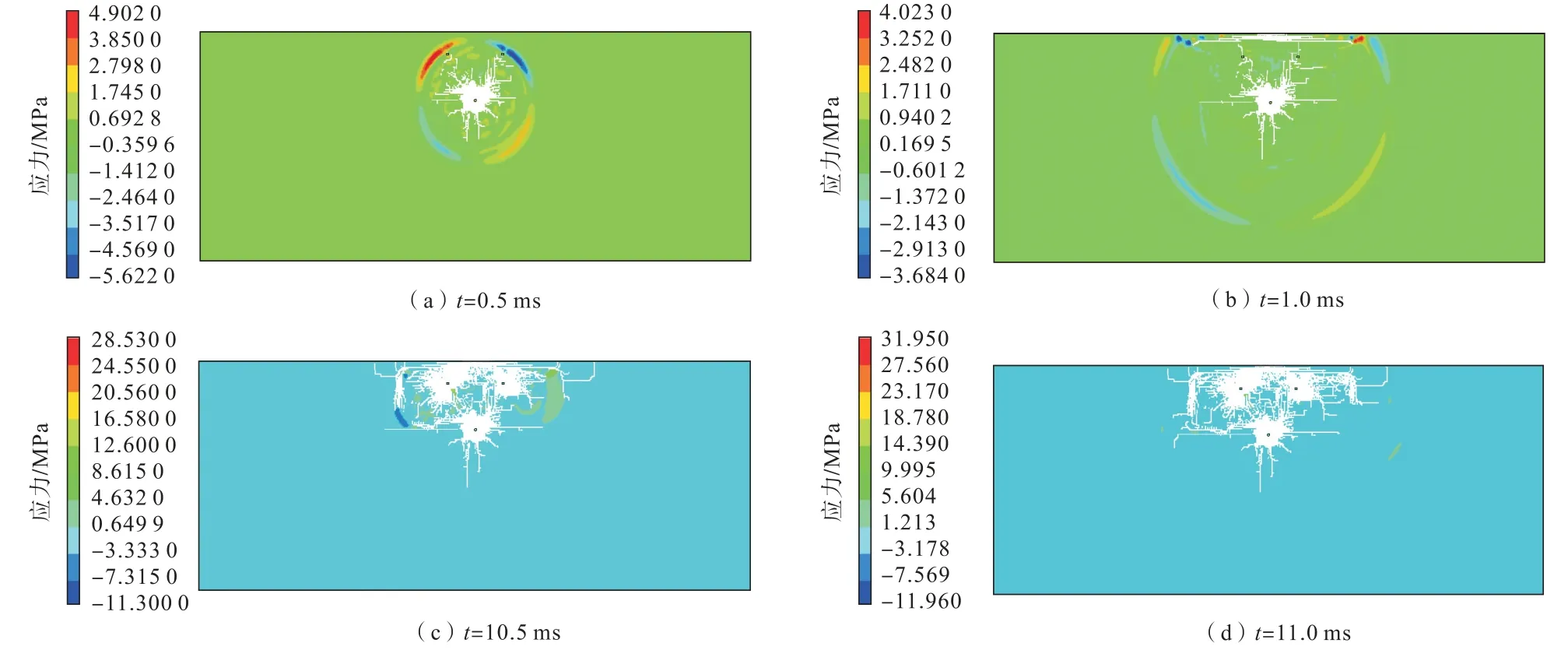
图2 方案2延时10 ms的爆破应力云图Fig.2 Blasting stress nephogram of scheme 2 with a delay of 10 ms

方案2是后排孔先起爆，在初始的后排孔先起爆阶段，炮孔抵抗线相对更大，岩体的夹制作用更为明显，但与方案1相同，爆炸应力波依然是从爆心开始以圆形向外传播，并在爆源附近形成明显的破裂区;当应力波传播至自由面时引起一定范围的岩体拉伸破坏。

在前排孔起爆阶段，炮孔两侧都有较好的自由面，其中一侧是计算模型自由面，另一侧是后排孔爆破创造的破碎空间;此时炮孔两侧的岩体夹制作用更小，在两孔同时起爆后可以取得较好的破岩效果。

2.2 爆炸破岩量对比

为反映不同延时间隔对爆破破岩的影响规律，在数值计算过程中引入失效计算模块，岩石材料的失效判据是由抗压强度和抗拉强度双重控制。采用单元失效范围表示破岩量，反映爆破体积的大小。相同装药量条件下，岩体失效单元数量越多，说明炸药单耗越小。两种方案的失效单元变化曲线如图3所示。

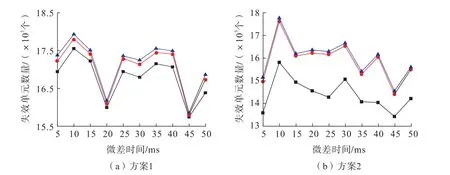
图3 两种方案不同延时的失效单元Fig.3 Failed units under different delays of two schemes

由图3(a)可知:对于方案1，同一延时间隔下，在起爆时间从t=0.5 s到t=1.5 s的过程中，反映了爆破裂隙的扩展过程;随着起爆时间的增加，模型失效单位数量逐渐增大。同一起爆时间下，随着延时间隔的增加，模型失效单元数量整体分为3个阶段，分别为20 ms以内、20～45 ms时间段和45～50 ms时间段。第1阶段，模型失效单元数量表现为先增加后减小变化趋势，在后排孔延期10 ms起爆时，获得最大破岩量。第2阶段，失效单元数量呈现上下波动现象;在后排孔延期35 ms起爆时，获得最大破岩量;而在45 ms时破岩量最小，20 ms时次之。在第3阶段，模型失效单元数量虽有一定的增加，但相比第1和第2阶段，仍然相对较小。

由图3(b)可知:对于方案2，与方案1类似，同一延时间隔下，在起爆时间从t=0.5 s到t=1.5 s的过程中，爆破裂隙不断扩展增大，表现出模型失效单元数量逐渐增加;t=0.5 s时的失效单元数量明显小于t=1.0 s、1.5 s，且t=1.0 s和t=1.5 s时的破岩量基本一致、差距很小，据此可以认为在t=1.5 s时爆炸破岩过程已经结束。同时，同一起爆时间下，随着延时间隔的增加，模型失效单元数量呈现出先增加后波动降低的变化规律;且在延时10 m时获得最大破岩量。

两种方案的爆破破岩对比如图4所示。从最终破岩量来看，除了延时间隔20 ms外，其他延时间隔下，方案1的破岩量都比方案2大，模型失效单元数量增幅为0.99%～14.83%;其中在延时间隔10 ms时，两种方案的破岩量同时达到峰值，此时二者的失效单元数量差值最小，仅为0.99%。进一步说明了延时间隔和起爆顺序对爆破破岩量的影响机制，同时说明自由面条件对于改善破岩效果、提高破岩量具有积极作用;对于自由面较好的方案1，岩体夹制作用小，可以获得更好的破岩效果。

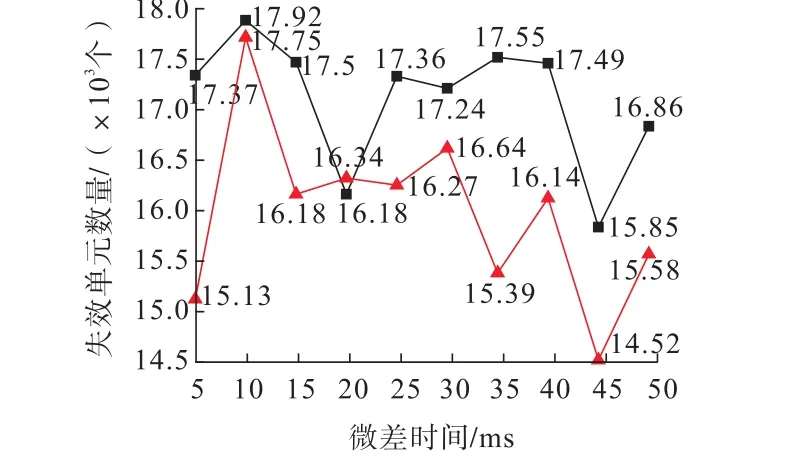
图4 两种方案爆破失效单元对比Fig.4 Comparison of blasting failure units in two schemes

方案1和方案2布孔方式相同，仅起爆方案不同;两种方案皆在微差延时10 ms时获得最大破岩量，且前者比后者增大0.99%。由此可知，无论前后排起爆顺序如何，最佳延时都相同;即前后排起爆顺序不影响最佳延时间隔，但影响最终破岩量大小。综上分析可知:对于爆破破岩量角度而言，同等炸药量下，为获得最大的破岩范围，推荐前后排孔之间的最佳延时间隔为10 ms。

2.3 爆破振动分析

以方案2为例，在计算模型上按照距离爆心由近至远的顺序依次提取了80050#和86017#两个测点的振动速度，对不同延时间隔的爆破振动速度大小进行对比，结果如图5所示，其中80050#测点的振动速度变化曲线如图6所示。

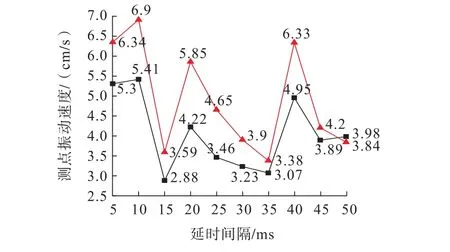
图5 测点振动速度与延时关系曲线Fig.5 Relationship between vibration speed and delay of measuring points

由图5、图6可知:延时间隔对测点爆破振动速度的影响明显;随着延时间隔的增加，测点振动速度整体呈现步调一致的波动变化趋势，且在10 ms间隔时分别取得最大值6.90 cm/s和5.41 cm/s，在40 ms间隔时为次大值，分别为6.33 cm/s和4.95 cm/s。同时，除了延时间隔50 ms以外，其他延时下80050#测点的振动速度都比86017#测点大，增大幅度为8.05%～38.59%，与近区振动大、远区振动小的规律相吻合，反映了振动速度随距离增加的衰减规律。

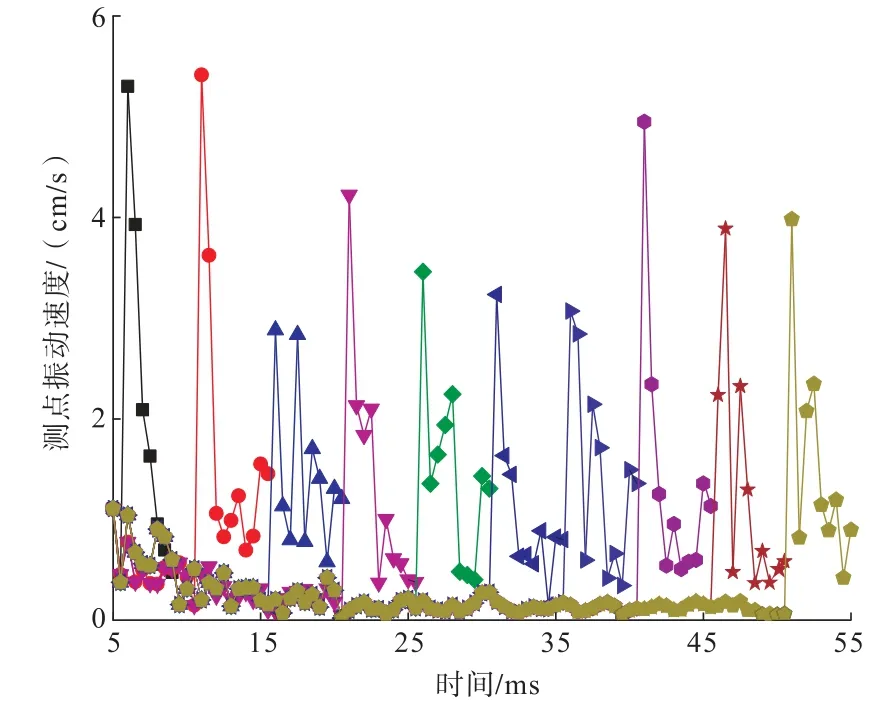
图6 80050#测点振动速度变化曲线Fig.6 Curves of vibration velocity of 80050#measuring point

综上分析可知:虽然在延时间隔10 ms时可取得最大破岩量，但测点振动速度也最大;因此，应需要综合考量爆破振动和破岩量两个指标，在爆区周边需要保护建(构)筑物的安全允许范围内，宜优选破岩量最大的延时间隔，以取得最佳经济效益。

3 三维模型下不同延时破岩规律

开展初始荷载30 MPa下的三维数值模拟分析，研究加载下延时间隔对爆破破岩的影响规律，同时与准二维模型进行对比，为确定合适的延时间隔提供理论依据。

3.1 爆炸破岩量对比

延时间隔10 ms的爆破模型位移云图如图7所示，不同延时的模型失效单元数量如图8所示。

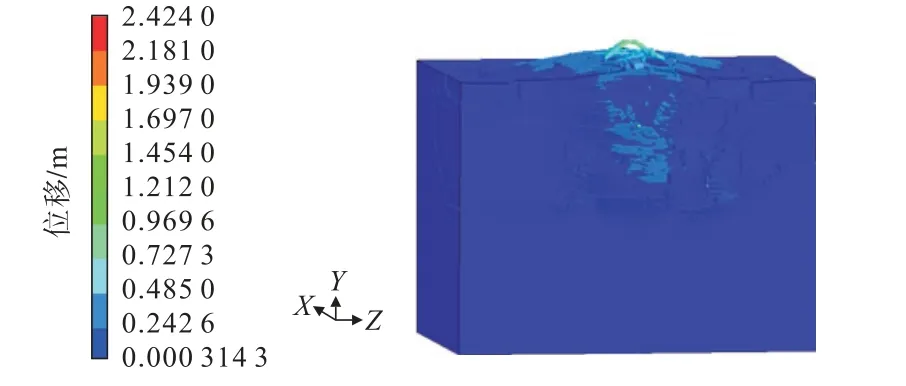
图7 10 ms延时模型位移云图Fig.7 Displacement nephogram of 10 ms delay model

由图7、图8可知:同一延时间隔下，随着炮孔起爆时间的延续，从1 ms到10 ms，模型失效单元数量逐渐增大，直至达到爆破结束t=10 ms时的破岩量。相同起爆时间下，随着延时间隔的增加，爆破破岩量呈现明显的波浪形变化规律;且在延时间隔10 ms时取得最大破岩量，此时炸药单耗最小，而延时间隔30 ms时破岩量最小。相比延时30 ms，延时10、15、20、25、40、50 ms的破岩量分别增大了8.20%、4.15%、5.37%、3.46%、6.64%、6.55%。说明延时间隔对于破岩量具有明显的影响，选择适宜的微差时间对于提高爆破量、降低成本具有积极意义。

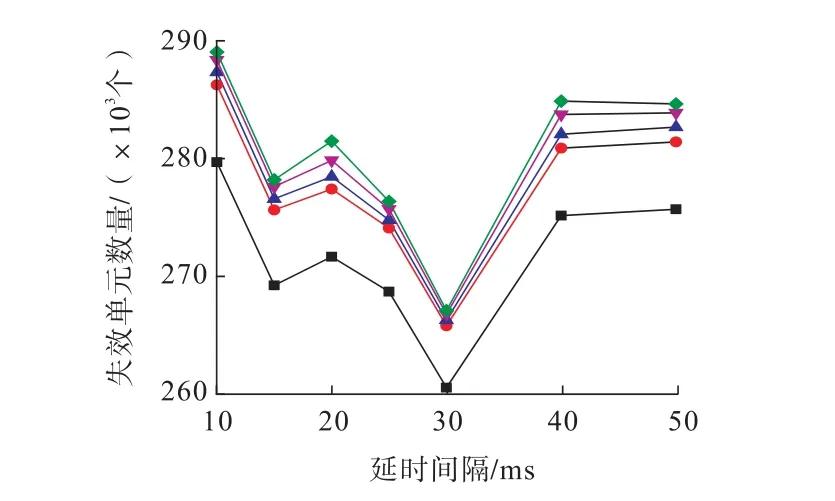
图8 不同延时模型的失效单元数量Fig.8 Number of failed units with different delay models

3.2 爆破振动分析

在数值计算模型上提取了不同延时674734#测点的爆破振动速度，如图9和图10所示。

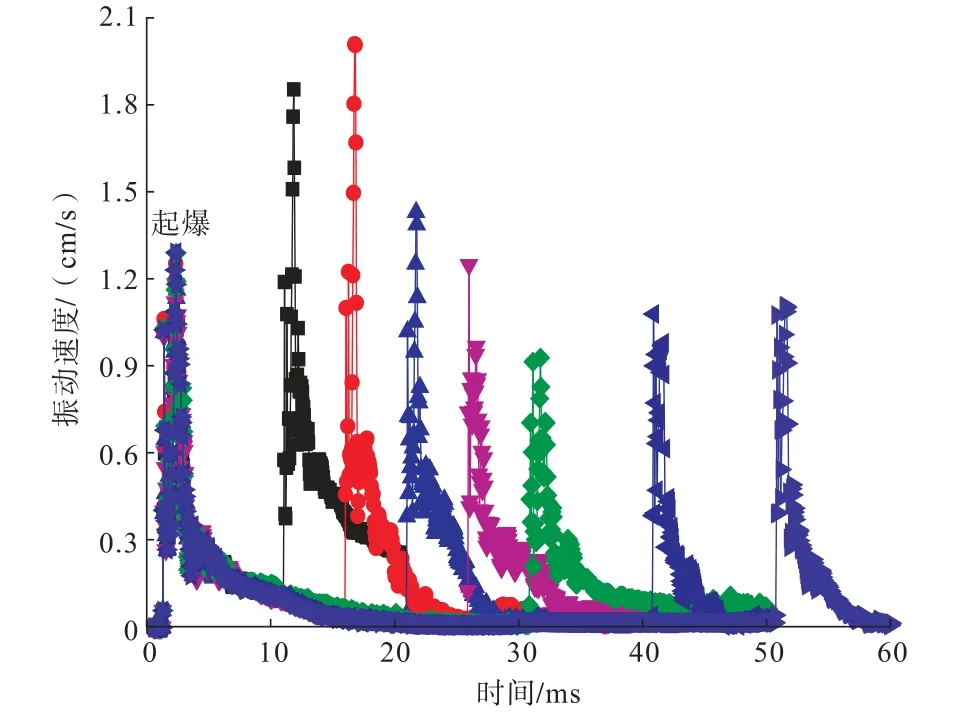
图9 674734#测点振动速度变化曲线Fig.9 Velocity curves of blasting velocity of 674734#measuring point

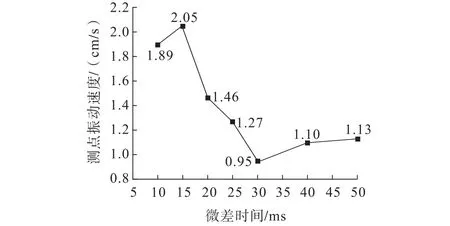
图10 674734#测点振动速度与延时间隔的关系Fig.10 Relationship between vibration velocity of 674734#measuring point and delay interval

由图9、图10可知:随着延时间隔的增加，测点振动速度整体上呈现出“先增大—后减小—再增大”的变化趋势，延时15 ms和30 ms为振动速度的两个拐点，分别对应最大振动速度2.05 cm/s和最小振动速度0.95 cm/s;而在延时10 ms取得第二大振动速度1.89 cm/s。

综上分析可知:考虑最大爆破破岩量，最佳的延时间隔为10 ms，但此时的测点振动速度也相对较大。因此，应综合考虑两者的平衡，优选适宜的延时间隔;在保护对象的振动速度安全允许范围内，适宜选择获得最大破岩量的延时，以取得最佳经济效益。

4 地下矿山现场应用

某地下矿山采用进路式开采方式，进路宽度6 m、高度7.5 m，分为上下两步骤回采，其中，上方3.5 m采用水平孔先爆，下方4 m采用台阶式垂直下向孔后爆。

试验区域的矿石坚硬，结合每台班钻孔进度，每次爆破2排炮孔，孔径80 mm，排距1.7 m，孔深4.5 m，堵塞1.6 m，单孔装药量16 kg。考虑到矿山爆破器材的种类，采用高精度导爆管雷管进行试验，首爆孔与次爆孔之间延时间隔为9 ms，与数值模型计算的10 ms基本一致。共计开展了12次现场试验，使用炸药1 346 kg，爆破量2 741.8 t，起爆网路见图11，爆破效果如图12所示。

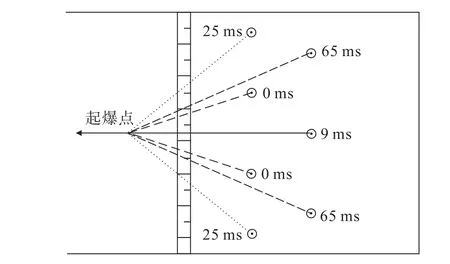
图11 起爆网路示意Fig.11 Schematic of the detonating network

图12 现场爆破效果照片Fig.12 Pictures of blasting effect in field test

现场试验表明:采用选取的延时间隔后，爆破块度较为均匀，无根底产生，未见爆破大块，铲装效率高，且爆破振动控制在安全范围内，较好地验证了延时间隔设置的可行性。

5 结 论

(1)延时间隔对于破岩量存在一定的影响，随着延时的增加，爆破破岩量呈现波动变化规律，且在延时10 ms取得最大破岩量;起爆顺序不会改变取得最大破岩量时的延时间隔，但对最终破岩量大小存在明显影响;前排孔先起爆优于后排孔先起爆，说明了自由面对于破岩具有积极贡献。

(2)在取得最大破岩量时的测点振动速度也较大。应根据现场实际条件，综合考虑振动速度和破岩量两个指标，在待保护建(构)筑物振动速度的安全允许范围内，优先考虑爆破破岩量，以提高生产效率、获取最佳经济效益。

(3)基于矿山岩性条件和试验参数，采用确定的延时间隔，可以取得较好的爆破破岩效果，控制采场大块率，提高铲装运输效率，较好地证明了本研究延时设置的可靠性。