基于天牛群优化算法的灌区渠系配水研究

田桂林，苏 枫，邹 红，吕谋超，申继先，秦京涛，范习超

▪灌溉水源与输配水系统▪

基于天牛群优化算法的灌区渠系配水研究

田桂林1,2，苏 枫3，邹 红4，吕谋超1*，申继先3，秦京涛1，范习超1

（1.中国农业科学院 农田灌溉研究所/农业农村部节水灌溉工程重点实验室，河南 新乡 453002；2.中国农业科学院 研究生院，北京 100081；3.河南省豫北水利工程管理局，河南 新乡 453002；4.新乡市大功引黄供水有限责任公司，河南 封丘 453300）

【目的】验证改进后的天牛群优化算法在渠系配水领域的科学性与适用性。【方法】以2020年大功灌区某次灌水过程为基础数据，以西一干渠干、支二级渠系输水过程中渗漏损失水量为优化目标，各渠道运行时间及下级支渠输水流量为决策变量，构建渠系配水模型，采用天牛群优化算法进行模型优化求解，并与天牛须搜索算法、粒子群算法等求解结果进行对比分析。【结果】采用天牛群优化算法求解得到的总配水量为391.85万m3，渗漏总水量为22.87万m3，配水总时间为7.30 d，相较于天牛须搜索算法计算的配水结果均有较大提升，与粒子群算法求解结果接近，但天牛群优化算法得出的渠系配水方案更为合理。【结论】改进后的天牛群优化算法能够较好满足灌区渠系水资源优化配置要求，为灌区水资源管理提供新的配水方法与科学建议。

灌区；渠系；优化配水；天牛群搜索算法；粒子群算法

0 引言

【研究意义】我国大中型灌区作为农业主要的用水与耗水部门，其有效灌溉面积3.47×107hm2，占全国耕地面积的25%，粮食产量占全国总量的50%[1]，年均灌溉用水量占全国农业灌溉用水总量的65%[2]，是保障我国粮食生产的主战场和农业节水的重要领域。水资源短缺一直是制约我国农业发展的重要因素，2020年《中国水资源公报》显示，我国农业用水总量3 612.4亿m3，占全国总用水量的62.14%，其中，农田灌溉水有效利用系数为0.565，保障农业水资源是促进农业发展的重要基础。灌区作为农业发展的基础设施，存在着水资源分配不合理、用水效率低等问题[3]。灌区渠系是灌溉水的输送载体，经验性的渠系水资源配水会导致水量损失、灌溉水利用率低等问题。将多种按需配水模型与科学的数学方法相结合，优化渠系现有的配水方案，提高灌溉水输水效率，缩短输水时间，减少灌溉水无效损失，对于缓解农业用水紧张和发展节水农业具有重要意义。

【研究进展】早在1995年，Kennedy和Eberhart结合鸟群觅食行为提出了粒子群算法（Particle swarm optimization PSO）[4]。粒子群算法作为一种群体智能算法，具有良好的全局寻优能力，一经提出便得到了广泛的研究与应用[5]。近年来，粒子群算法逐渐被应用于解决如农田水文学研究、需水量计算与预测、渠系建筑物优化改进等各类农业水利工程问题[6-8]。其中，部分研究学者也将其与配水模型相结合，优化现有配水方案，取得了大量研究成果。张国华等[9]结合粒子群优化算法求解0-1规划的渠道轮灌优化配水模型，计算得出的轮灌组引水方案，持续时间均匀性较好。随后粒子群算法在配水领域的应用不断成熟，衍生出多种改进后的粒子群算法，以适配多种应用场景，改进后的算法优化效果明显。褚宏业等[10]为解决高原灌区水管理落后问题，建立了多目标配水模型，并使用粒子群算法与遗传算法分别进行方案求解，二者计算结果均能满足模型要求，但粒子群算法运算速度占优且调度方案更为合理。刘照等[11]将渠系配水中传统的“定流量、变历时”的工作方式改为“变流量，变历时”，以此建立多目标配水模型，采用双层粒子群算法求解最优轮灌组合，为灌区管理部门制定配水计划提供了决策依据。王庆杰等[12]将配水过程中“组间续灌、组内轮灌”的渠道配水方式变更为“组间轮灌、组内续灌”，并在基础粒子群算法中融入模拟退火思想和遗传算法中的交叉变异算子，以此来改进粒子群算法，模型求解出的配水方案能够实现集中、高效配水。李彤姝等[13]以水流过渡平稳、渠道渗漏量最小为目标建立了多目标配水模型，使用改进后的多目标粒子群优化算法（MOPSO）进行求解，结果表明，较回溯搜索法和向量评估遗传算法，多目标粒子群算法计算的配水时间有所缩短，配水方案更优。粒子群算法及其改进算法在渠系优化配水研究中表现出了较好的合理性与适用性，应用渐趋成熟。

随着水资源优化配置领域的研究深入，越来越多的智能算法被应用于优化配水研究中。Jiang等[14]受天牛觅食启发，提出了天牛须搜索算法（Beetle Antennae Search，BAS）。该算法已逐渐应用于PID控制器、电力调度、定位、经济管理、路径规划以及图形处理等多项领域[15]，但在灌溉配水中研究较少。田桂林等[16]将天牛须搜索算法（BAS）应用于引黄灌区渠系单目标优化配水模型求解中，发现天牛须搜索算法求解结果可满足灌区配水要求，有效减少了渠系渗漏损失，但天牛须搜索算法作为单体智能算法，较为依赖初始值选定，易陷入局部最优，尚有较大的改进空间。2018年，为改进天牛须搜索算法在解决高维复杂问题上过度依赖初始值及计算效率上的不足，Wang等[17]将粒子群算法与天牛须搜索算法相结合，提出了天牛群优化算法。目前，该算法已被应用于传感器布置优化、微电网优化调度等[18-19]领域，且应用范围逐渐扩大。【切入点】随着渠系配水实际运行情况复杂性增大，学者们逐渐将多种算法交叉融合后进行模型的优化求解，以提高求解速度与结果的准确性。天牛群优化算法在天牛须搜索算法的框架上结合了成熟粒子群算法的迭代更新机制进行改进，将其应用于渠系配水研究，可构建更为科学合理的渠系优化调度模型。【拟解决的关键问题】本文以大功灌区西一干渠及其支渠为研究对象，构建以渗漏量最小为目标的渠系配水模型，结合天牛须搜索算法、粒子群算法及天牛群优化算法3种方法进行求解，得出支渠开、关闸时间及输水流量。同时将3种算法配水方案进行对比分析，判别改进后的天牛群优化算法在渠系优化配水上的科学性与适用性，以期为灌区水管理提供新的模型优化方法与合理建议。

1 渠系优化配水模型及算法

1.1 渠系配水模型构建

为提高灌区渠系配水效率，减少灌溉水无效损失，在天牛须搜索算法（BAS）的基础上，进一步结合改进后的天牛群搜索算法（BSO）优化配水结果，并同粒子群算法（PSO）进行比较分析，验证改进后的天牛群算法在渠系配水中的适用性。本研究以渠系渗漏损失水量最小为优化目标，以下级渠道闸门启闭时间与二级渠道输水流量为决策变量建立配水模型，使用天牛群搜索算法与粒子群算法分别求解。

1）目标函数

2）基本公式

流量计算式为：

式中：q毛为支渠的渠道毛流量（m3/s）；Q毛为时段时，干渠渠道毛流量（m3/s）；（T）具体含义详见式（15），其余符号意义同前。

时间计算式为：

3）约束条件

流量约束：

水量约束：

时间约束：

判别约束：

4）二级渠系水利用系数计算式[20-21]为：

模型中计算渠系输水渗漏水量、流量及时间公式，以及所采用的渠道流量加大、最小系数，均参照《灌溉排水工程学》[21]。

1.2 天牛群优化算法（BSO）

天牛须搜索算法（BAS）是Jiang等[14]在2017年提出的一种单体智能算法，在解决高维计算问题时表现一般，易陷入局部最优，该算法已被应用于灌区渠系优化配水研究[16]。Wang等[17]结合粒子群算法（PSO）的优化机制，将2种算法结合，提出了天牛群优化算法（BSO），BSO算法将初始的一只天牛扩展为一个群体，消除了初始值对算法求解结果的限制。整体算法框架借鉴了PSO算法的群体寻优过程与极值更替，在单个天牛个体的迭代更新过程中使用了BAS算法的左右须更新机制，从而发挥2种算法各自的优点，以实现问题求解。

天牛群体位置更新公式：

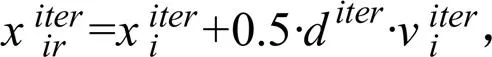
天牛群体速度更新公式：

其他参数计算式为：

通过上述公式计算并更新天牛群的位置与速度值，完成个体与群体极值的更新，不断迭代至最大迭代次数，完成模型求解，得出优化后的计算结果。

2 研究区概况

本研究以河南省新乡市大功灌区为研究区域，选取大功灌区渠首西一干渠为优化对象。大功灌区总面积31.92万hm2，属于温带大陆性季风气候，多年平均气温13.7 ℃，年均无霜期207 d，灌区范围内热量丰富，年平均日照时间2 362 h，年日照率52%。灌区年平均蒸发量为1 921.5 mm，灌区年平均降水量565.7 mm，灌区范围内降水年际变化较大，年内分配不均，利用率低，其中，7、8、9月的降水量占全年降水量的60%左右。大功灌区及西一干渠渠系分布见图1，西一干渠下级渠道包含汪寨加支渠、一支至十支等10条支渠，具体参数见表1。大功灌区现状渠系水利用系数为0.560，灌溉水利用系数为0.495。本次计算以2020年大功灌区某次灌水数据为准，轮灌周期为20 d，灌水定额为675 m3/hm2，年引水量为3 143.18万m3，该轮计划灌溉水量391万m3。

图1 大功灌区及西一干渠渠系分布图

表1 西一干渠渠系各项参数

3 基于多种优化算法的模型求解

3.1 天牛群优化算法（BSO）模型参数设置

表2 配水模型计算公式参数

3.2 3种算法求解结果

将配水模型结合优化算法进行求解，在进行多次重复计算与结果筛选后，得到了西一干渠各支渠的渠道配水时间计划，图2、图3分别为天牛群优化算法（BSO）、粒子群算法（PSO）计算结果。通过对比2种算法的求解结果发现，各干渠闸门启闭时间分布及整体配水时间长短接近，重合度较高。由图2可知，BSO算法优化求解的配水计划将灌水时间缩短至7.30 d，而图3所示的PSO算法中，配水时间为7.43 d。二者的灌水周期接近且BSO算法求解结果在配水时间长短上略优于PSO算法。相较于传统经验性灌水周期20 d，2种算法的优化结果将灌水效率提高了近65%，缩短了近半程灌水时间。

图2 天牛群优化算法（BSO）配水时间

图3 粒子群算法（PSO）配水时间

在模型及其他条件相同的情况下，采用天牛须搜索算法（BAS）进行求解，所得配水结果[16]如图4所示，相较于单体智能算法BAS算法，BSO、PSO算法优化求解后的灌水时间分别缩短了5.95、5.82 d，配水效率提高了近45%。

图4 天牛须搜索算法（BAS）配水时间

3种算法优化后的干、支渠的渠道流量变化情况如图5、图6所示。由图5可知，BSO算法与PSO算法优化求解的各支渠流量结果相近，均处于加大和最小流量之间，其中，西一干二支渠、四支渠、八支渠、十支渠及汪寨加支渠的流量大小接近设计流量，从而保证渠道良好的运行状态。而BAS算法求解的各支渠流量均处于设计流量与最小流量之间，较另外2种算法整体流量偏低，支渠运行流量偏低是导致BAS算法整体灌水时间较长的直接原因之一。

配水研究中各支渠流量的变化会影响干渠流量大小。如图6所示，3种算法所求解的西一干渠渠道流量随配水时间的变化情况。BSO与PSO算法优化后的干渠配水流量最大分别可达到8.81、8.59 m3/s，配水平均流量分别为6.21、6.19 m3/s，整体流量水平较高。BSO算法优化求解的干渠平均流量略优于PSO算法，使得BSO算法求解的灌水时间略短于PSO算法，配水效率更高。而BAS算法求解结果中，干渠最大流量6.84 m3/s，整体流量长时间保持在4.0～6.5 m3/s，干渠配水流量偏低导致整体配水时间较长。

图5 西一干渠各支渠流量分布

图6 西一干渠流量分布

图7为3种算法优化求解的各支渠总配水量，BSO算法与PSO算法所求得的配水量结果同各支渠计划配水量结果接近一致，仅在西一干渠二支渠时，PSO算法配水量略高于计划配水量。而BAS算法的配水时间过长，导致各支渠配水量整体偏多，高于其他2种算法所求得的配水量。

图7 西一干渠各支渠总配水量分布情况

如表3所示，BSO算法与PSO算法优化后得到的总配水量分别为391.85万、397.54万m3，所求解的模型目标函数渗漏总水量分别为22.87万、22.89万m3。BSO算法所求渗漏总水量较PSO算法更少，且配水时间更短。BAS算法求解的整个渠系渗漏总水量为34.99万m3，占总配水量的6.69%，与另外2种算法相比，计算结果差距较大。依据式（16）—式（18）计算出的3种算法配水结果的二级渠系水利用系数均高于0.7，相较于现状渠系水利用系数0.560有较大提高。从上述结果可以看出，3种算法通过优化求解配水模型，合理调整渠道闸门启闭时间及渠道流量，在一定程度上提高了灌溉效率与水资源利用率，减少了灌溉水在输送过程中的损失。

表3 3种算法计算结果

图8与图9为BAS算法与PSO算法的迭代图，由图9可知，BSO算法在迭代65次左右接近极值点，而PSO算法则是在90次左右接近极值点。由于2种算法位置更新公式间的差异，使得PSO算法在迭代40次前，寻优能力及下降速度较BSO算法更优，随着次数增加，逐渐趋近极值，BSO算法的寻优速度加快，先于PSO算法找到极值点，迭代效率略优于PSO算法，且最优解结果较PSO算法更好。

图8 2种算法迭代云图（上：PSO，下：BSO）

4 多种求解算法对比分析

4.1 天牛群优化算法与天牛须搜索算法对比分析

BSO算法计算出的配水结果在BAS算法求解结果的基础上优化效果较为明显。在相同的配水模型下，分别使用BAS与BSO算法求解渠系配水方案，通过对比发现，BSO算法计算出的总配水量、渗漏总水量更少，干、支渠配水流量更大，使得各支渠的配水时间更加集中，灌水时间缩短近6 d，而各支渠计算的输水总量也更加接近计划水量，提高了输水效率。BSO算法将BAS单体算法与PSO群体算法相结合，改进并克服了BAS算法在高维寻优问题上依赖初始值选定与易陷入局部最优等问题。同时，由于BAS算法为单体智能算法，参数设置较少，使得BAS算法在求解过程中计算量小，迭代次数少，寻优速度快。在与BSO算法对比中可得，改进后的BSO算法在计算量增大的同时迭代次数较BAS算法并未存在较大的差异，寻优速度与BAS算法基本一致，寻优效率显著提高。

图9 2种算法迭代图

4.2 天牛群优化算法与粒子群算法对比分析

BSO算法在复杂的灌区渠系优化配水研究中表现良好。PSO算法在配水研究中应用广泛，适用于单目标、多目标等多种配水模型，且表现出较好的适用性。从上述求解结果中对比2种算法可以发现，BSO算法求解出的总渗漏量以及总灌水时间等更为合理，求解过程的迭代次数更少，求解结果更趋近最优解。BSO算法结合了BAS算法的“左右须”求值机制，使得天牛在迭代时的位置更新更具有指向性，寻优能力增强，且寻优效率更高。BSO搜索算法在求解灌区渠系单目标优化配水模型中表现出较好的适用性与合理性。目前，随着配水模型复杂程度的提高，渠系配水逐渐趋于多目标模型，尚且缺乏BSO算法在多目标配水模型中的研究与应用，具有一定的改进空间。

5 结 论

1）将天牛群优化算法运用到灌区渠系优化配水模型中，所得配水结果能够满足灌区灌水基本要求。在满足干、支渠输水流量及灌区灌水周期的前提下，配水方案可保证渠道集中灌水，缩短配水时间、减少渗漏水量、提高渠系水利用系数。在保证模型目标最优的前提下，大幅度缩短了灌水时间。

2）通过与BAS、PSO算法的对比，BSO算法在求解高维优化配水问题上表现良好。BSO算法在保留BAS算法快速寻优的基础上，充分结合PSO算法群体性优势，显著优化了配水结果，改进了BAS算法过度依赖初始值选定、易陷入局部最优等不足。同时，与PSO算法相比，BSO算法迭代次数少，求解速度快，求解结果更加接近最优值。

综上所述，天牛群优化算法能够解决复杂的渠系优化配水模型求解的问题，对于提高灌区用水管理效率具有一定的指导意义。

[1] 陈明忠. 加快推进灌区现代化改造 促进灌区高质量发展[J]. 中国水利, 2021(17): 1-3.

CHEN Mingzhong. Accelerating modernization of irrigation district for high quality development[J]. China Water Resources, 2021(17): 1-3.

[2] 马颖卓. 加快灌区现代化改造与节水技术应用 促进黄河流域生态保护和高质量发展：访中国工程院院士康绍忠[J]. 中国水利, 2021(17): 4-7.

MA Yingzhuo. Speeding up modernization of irrigation district and application of water-saving technology for promoting ecological protection and highquality development in the Yellow River Basin: Interview with Kang Shaozhong, academician of Chinese Academy of Engineering[J]. China Water Resources, 2021(17): 4-7.

[3] 齐学斌, 黄仲冬, 乔冬梅, 等. 灌区水资源合理配置研究进展[J]. 水科学进展, 2015, 26(2): 287-295.

QI Xuebin, HUANG Zhongdong, QIAO Dongmei, et al. Research advances on thereasonable water resources allocation in irrigation district[J]. Advances in Water Science, 2015, 26(2): 287-295.

[4] KENNEDY R, EBERHART J. Particle swarm optimization[C]//Proceedings of IEEE International Conference on Neural Networks. Perth, Australia: IEEE, 1995: 1 942-1 948.

[5] 何国华, 解建仓, 汪妮, 等. 基于模拟退火遗传算法的水资源优化配置研究[J]. 西北农林科技大学学报(自然科学版), 2016, 44(6): 196-202.

HE Guohua, XIE Jiancang, WANG Ni, et al. Optimal allocation of water resources based on simulated annealing-genetic algorithm[J]. Journal of Northwest A & F University (Natural Science Edition), 2016, 44(6): 196-202.

[6] 邓婵, 李纯, 李梦琪, 等. 粒子群算法在农业水文学中的应用进展[J]. 安徽农业科学, 2021, 49(8): 16-20, 29.

DENG Chan, LI Chun, LI Mengqi, et al. The application of particle swarm optimization in agricultural hydrology[J]. Journal of Anhui Agricultural Sciences, 2021, 49(8): 16-20, 29.

[7] 许昆. 涑水河流域生态环境需水量计算和预测[J]. 灌溉排水学报, 2016, 35(11): 107-110.

XU Kun. Calculation and prediction of water demand of the ecological environment in Sushui River Basin[J]. Journal of Irrigation and Drainage, 2016, 35(11): 107-110.

[8] 张伟, 何武全. 基于粒子群算法的抛物线形渠道断面优化方法[J]. 灌溉排水学报, 2017, 36(4): 94-98.

ZHANG Wei, HE Wuquan. Optimizing channels with parabolic cross-section using the particle swarm method[J]. Journal of Irrigation and Drainage, 2017, 36(4): 94-98.

[9] 张国华, 张展羽, 邵光成, 等. 基于粒子群优化算法的灌溉渠道配水优化模型研究[J]. 水利学报, 2006, 37(8): 1 004-1 008, 1 014.

ZHANG Guohua, ZHANG Zhanyu, SHAO Guangcheng, et al. Optimization model for discharge distribution of irrigation channels based on particle swarm optimizer[J]. Journal of Hydraulic Engineering, 2006, 37(8): 1 004-1 008, 1 014.

[10] 褚宏业, 王莹, 文俊, 等. 遗传算法和粒子群算法求解渠系多目标优化模型[J]. 中国农村水利水电, 2015(4): 9-11, 17.

CHU Hongye, WANG Ying, WEN Jun, et al. Genetic algorithm and PSO algorithm for solving canal system multiobjective optimization model canal[J]. China Rural Water and Hydropower, 2015(4): 9-11, 17.

[11] 刘照, 程帅, 李华朋, 等. 基于双层粒子群算法的下级渠道流量不等时渠系优化配水[J]. 干旱地区农业研究, 2017, 35(3): 88-93, 237.

LIU Zhao, CHENG Shuai, LI Huapeng, et al. Optimal water allocation in canal system under unequal discharges in subordinate canals based on Bi-level PSO Methoo[J]. Agricultural Research in the Arid Areas, 2017, 35(3): 88-93, 237.

[12] 王庆杰, 岳春芳, 李艺珍, 等. 基于改进粒子群算法的两级渠道水资源优化配置[J]. 干旱地区农业研究, 2019, 37(4): 26-33.

WANG Qingjie, YUE Chunfang, LI Yizhen, et al. Optimal allocation of water resources with two-level channel based on improved particle swarm optimization algorithm[J]. Agricultural Research in the Arid Areas, 2019, 37(4): 26-33.

[13] 李彤姝, 黄睿, 孙志鹏, 等. 基于多目标粒子群算法的渠系优化配水研究[J]. 灌溉排水学报, 2020, 39(9): 95-100, 125.

LI Tongshu, HUANG Rui, SUN Zhipeng, et al. Optimizing water distribution in canal networks using multi-objective particle swarm optimization method[J]. Journal of Irrigation and Drainage, 2020, 39(9): 95-100, 125.

[14] JIANG X, LI S. BAS: Beetle Antennae Search Algorithm for Optimization Problems[J]. arXiv, 2017, 1 710: 10 724.

[15] 廖列法, 杨红. 天牛须搜索算法研究综述[J]. 计算机工程与应用, 2021, 57(12): 54-64.

LIAO Liefa, YANG Hong. Review of beetle antennae search[J]. Computer Engineering and Applications, 2021, 57(12): 54-64.

[16] 田桂林, 吕谋超, 苏枫, 等. 基于天牛须搜索算法的渠系优化配水初步研究[J]. 节水灌溉, 2021(12): 38-42.

TIAN Guilin, LYU Mouchao, SU Feng, et al. Preliminary study on channel optimization water distribution based on beetle antennae search algorithm[J]. Water Saving Irrigation, 2021(12): 38-42.

[17] WANG T, LONG Y. Beetle swarm optimization algorithm: theory and application[J]. arXiv, 2020, 1 808: 00 206.

[18] 胥松奇, 周世良, 曹师宝, 等. 基于离散天牛群算法的高桩码头传感器优化布置[J]. 水运工程, 2020(6): 46-52.

XU Songqi, ZHOU Shiliang, CAO Shibao, et al. Sensor optimal placement of high piled-wharf based on binary beetle-swarm algorithm[J]. Port & Waterway Engineering, 2020(6): 46-52.

[19] 王怡云, 吴雷. 基于改进天牛群算法的微电网优化调度[J]. 电子测量技术, 2020, 43(16): 76-81.

WANG Yiyun, WU Lei. Optimization of micro-grid scheduling based on improved algorithm of beetle swarm optimization[J]. Electronic Measurement Technology, 2020, 43(16): 76-81.

[20] 陈浩, 周艳, 王朝江. 灌区渠道水利用系数计算和分析探讨[J]. 水利水电工程设计, 2020, 39(2): 21-23, 56.

CHEN Hao, ZHOU Yan, WANG Chaojiang, Calculation and analysis of water utilization coefficient in canal of irrigation area[J]. Design of Water Resources & Hydroelectric Engineering, 2020, 39(2): 21-23, 56.

[21] 史海滨, 田军仓, 刘庆华, 等. 灌溉排水工程学[M]. 北京: 中国水利水电出版社, 2014.

Calculating Water Distribution in Irrigation Channel Networks Using the Beetle Swarm Optimization Algorithm

TIAN Guilin1, 2, SU Feng3, ZOU Hong4, LYU Mouchao1*, SHEN Jixian3, QIN Jingtao1, FAN Xichao1

(1.Farmland Irrigation Research Institute, Chinese Academy of Agricultural Sciences/Key Laboratory of Water-saving Agriculture of Ministry of Agriculture, Xinxiang 453002, China; 2. Graduate School of Chinese Academy of Agricultural Sciences,Beijing 100081, China; 3. Yubei Water Conservancy Engineering Administration Bureau of Henan Province, Xinxiang 453002, China; 4.Xinxiang Dagong Diversion Yellow Water Supply Co. Ltd., Fengqiu 453300, China)

【Objective】Optimizing water allocation to channel networks in irrigation districts can reduce water waste and help improve water use efficiency. This paper presents the application of a modified beetle swarm optimization algorithm to achieve this goal.【Method】The analysis was based on irrigation in 2020 at Dagong irrigation district. Reducing water losses from seepage in the channel network was taken as the optimization objective, and operating duration of each channel and water discharge to the low-order branches were taken as the decision variables. We constructed water distribution in the channel network and solved the optimization using the beetle swarm optimization algorithm. The results were compared with those obtained from the beetle antennae search algorithm and the particle swarm algorithm.【Result】The total water distribution calculated from the beetle swarm optimization algorithm is 3 918 500 m3, the total loss from leakage is 228 700 m3, and the total water distribution time is 7.30 d. These are a great improvement compared with those obtained from the beetle antennae search algorithm, and close to the results calculated from the particle swarm algorithm.【Conclusion】The modified beetle swarm optimization algorithm is efficient and the results calculated by it meet the requirements for optimal allocation of water resources to channel network in irrigation district. It can be used to improve water management in irrigation districts and other areas.

irrigation district; canal system; optimal water distribution; beetle swarm optimization algorithm; particle swarm algorithm

1672 - 3317（2022）07 - 0096 - 08

S274.3

A

10.13522/j.cnki.ggps.2022093

田桂林, 苏枫, 邹红, 等. 基于天牛群优化算法的灌区渠系配水研究[J]. 灌溉排水学报, 2022, 41(7): 96-103.

TIAN Guilin, SU Feng, ZOU Hong, et al. Calculating Water Distribution in Irrigation Channel Networks Using the Beetle Swarm Optimization Algorithm[J]. Journal of Irrigation and Drainage, 2022, 41(7): 96-103.

2022-02-24

中国农业科学院农业科技创新工程项目（CX0001-04-2021）

田桂林（1997-），男。硕士研究生，主要从事灌区渠系优化配水研究。E-mail: ykerlove@163.com

吕谋超（1968-），男。研究员，博士生导师，主要从事节水灌溉理论与技术研究。E-mail: lvmouchao@aliyun.com

责任编辑：白芳芳