斑岩矿床侵入体顶部破裂系统形成的力学机制:多场耦合数值模拟的启示
常成, 罗纲
1 中国科学院计算地球动力学重点实验室, 中国科学院大学地球与行星科学学院, 北京 100049 2 武汉大学测绘学院, 武汉 430079 3 武汉大学地球空间环境与大地测量教育部重点实验室, 武汉 430079
0 引言
斑岩矿床是一种重要的经济矿床,其产出的金属包括了全世界约75%的铜,50%的钼,25%的金,以及少量的银、铅、锌等(Kirkham and Sinclair, 1995; Sillitoe, 2010; Richards, 2003, 2009, 2013; Richards and Mumin, 2013;Hou et al., 2015).在斑岩矿床中,铜和钼元素通常以网脉状或脉状-浸染状产出于花岗质侵入体的顶部和周围,并赋存于破裂的岩石中(Tosdal and Richards, 2001;Guillou-Frottier and Burov,2003;Sillitoe, 2010).近年来对斑岩矿床的研究表明,在不考虑热液与围岩相关的化学反应因素的情况下,侵入岩体周围的破裂、破碎带和角砾岩筒等破裂系统既是含矿热液的导流通道,又是含矿热液中矿质沉淀和最终矿体赋存的成矿空间(Burnham, 1985; Tosdal and Richards, 2001; Guillou-Frottier and Burov,2003; Stephens et al., 2004; 刘亮明, 2011; Dilles and John, 2021).因此,研究斑岩矿床侵入体周围破裂形成的物理力学机制,对于理解斑岩矿床的矿体就位过程以及找矿勘探工作都具有重要的指导意义.
斑岩矿床是典型的与岩浆有关的热液成矿系统.这类成矿系统是复杂的多物理场耦合系统,主要受到温度(thermal)、流体在孔隙介质中的流动(hydraulic)、力学作用(mechanical)和水-岩化学反应(chemical)四种主要因素的耦合控制(Hobbs et al., 2000; 池国祥和薛春纪, 2011; Poulet et al., 2012; Zou et al., 2017).以斑岩侵入体周围破裂系统的形成为例,前人的研究表明,浅部的花岗岩侵入体是成矿热液集中和热力学作用特别强烈的区域;高温花岗岩侵入体的加热作用、岩体中析出的岩浆水和挥发分、岩体侵入有关的力学过程以及上述过程之间的相互作用控制着侵入体周围破裂系统的形成(Tosdal and Richards,2001;Guillou-Frottier and Burov,2003).所以,在不考虑复杂的水-岩化学反应和矿质沉淀的情况下,全面地研究斑岩矿床中侵入体周围破裂系统的形成,需要包括热(T)-流体(H)-力学(M)三个因素的耦合作用,即THM耦合(Hobbs et al., 2000; Guillou-Frottier and Burov,2003; Poulet et al., 2012).
THM耦合模型已广泛应用于多项工程及灾害研究,包括地下核废料的贮藏、油气的产生和储存、地热能的开采、滑坡的产生和斜坡的稳定性等等(Jing and Feng, 2003).但是,很少有研究者将其应用到热液成矿系统这样的地质时间尺度问题(Poulet et al., 2012).原因主要有三个:第一,传统的矿床学研究方法注重于成矿温度和化学反应过程,对热液流体的流动模式以及成矿系统的动力学机制研究不足;第二,地球科学家们经常将复杂地质过程和问题概念化,并且识别出地质过程的一到两个主控因素进行调查研究;第三,三种以上的物理化学因素的耦合属于复杂的非线性多场耦合求解问题,计算常常不收敛,且所需的计算量很大.这些限制条件使得成矿动力学研究常常忽略了复杂的相互耦合反馈机制,但这些反馈机制常常是十分重要的(Hobbs et al., 2000; Guillou-Frottier and Burov,2003; Schardt and Large, 2009; Poulet et al., 2012).
目前大部分相关研究是对地质现象的观测(Tosdal and Richards,2001;Sillitoe, 2010),或者通过矿床中不同的破裂类型和应力莫尔圆来推断破裂的形成,而对岩浆侵入体周围的破裂形成力学机制研究较少(Stephens et al., 2004;刘亮明, 2011; Japas et al., 2021).前期研究者们通过解析的力学公式初步研究了侵入体周围破裂形成的力学机理,但随着计算机技术和数值计算方法的发展,数值模拟研究方法逐渐被用来进一步深入解释侵入体周围破裂形成的力学机制.Koide和Bhattachar(1975)通过推导解析的弹性力学公式和塑性屈服准则,初步研究了侵入岩体顶部可能形成的破裂样式和不同力学性质的破裂分带.Sartoris等(1990)通过有限元方法模拟了浅部岩浆房的不同形状、不同顶部侵入压力以及不同力学参数条件下岩浆房周围破裂的形成,但是没有耦合热和流体的作用.Guillou-Frottier和Burov(2003)通过耦合热传导、热膨胀与Mohr-Coulomb塑性屈服准则,研究了高温侵入体的热效应导致的岩体顶部破裂形成的动力学机制,但是没有考虑流体的作用;Zhang等(2012)通过耦合热传导与应力应变,建立了考虑剪切生热的位错-蠕变力学本构,研究了在挤压和拉张背景下岩浆房周围大断层的形成样式,但是该研究依然没有考虑流体对破裂的影响,并且其破裂的形成主要是构造加载导致的,仅对赋存于构造运动下形成的大断层中的矿床(剪切带型金矿床)具有重要意义.综上所述,对于斑岩成矿系统中岩浆侵入体周围的破裂形成力学机制研究,目前还缺乏热-流体-力学三场耦合的数值模型及其模拟研究.
为了研究岩浆热液成矿系统的物理力学过程及演化,本文首先建立了一个概念性的简化的柱状岩浆侵入体侵入到围岩中的二维孔隙热弹性平面应变有限元模型,通过耦合热传导、孔隙流体流动和应力应变(THM耦合),分析了高温岩浆的侵入对围岩中应力和应变状态的扰动和影响,验证了模型的正确性.然后,在模型中加入塑性,计算了塑性应变(即破裂)的形成与演化,通过分析偏应力、平均应力及孔隙流体的演化,来解释侵入体周围围岩的破裂形成和发育的力学过程.模拟计算发现偏应力在侵入岩体顶部围岩的集中是导致岩体顶部破裂形成的主要原因.最后,依据青藏甲玛铜多金属斑岩矿床的实际矿床剖面,建立了一个二维平面应变孔隙热弹塑性有限元模型,计算了侵入岩体顶部围岩破裂的形成.模型结果显示侵入岩体顶部围岩破裂发育情况与甲玛矿床岩体顶部的斑岩矿体和角岩矿体的容矿破裂系统具有一致性.这一结果解释了侵入体顶部围岩破裂系统形成和发育的力学机理,对矿产的勘探与开发有着重要的科学指导意义.
1 斑岩矿床岩体周围容矿破裂的地质概况
前人对斑岩矿床的地质研究表明,绝大多数斑岩矿床都可以简化为一个浅部的花岗岩侵入体侵入到以碳酸盐岩和火山碎屑岩为主的围岩中;侵入体被密集的网络或网脉状破裂系统所包围,其顶部可能发育脉体和角砾岩筒;这些破裂是成矿流体运移和沉淀的重要场所,即成矿空间或容矿空间(图1)(Kirkham and Sinclair,1995; Tosdal and Richards,2001; Guillou-Frottier and Burov,2003; Sillitoe,2010).如果以容矿破裂的类型来划分斑岩矿床,可以划分为两个主要类型:脉体为主的斑岩矿床和角砾岩为主的斑岩矿床(Tosdal and Richards,2001;Guillou-Frottier and Burov,2003).脉体为主的斑岩矿床以围绕深成岩体尖端的破裂、断层和裂隙网络为特征:在岩体顶部附近的脉体以及岩体顶部与围岩接触带的网脉状破裂系统中,通常发育较为高温的铜矿和铁矿,而距离岩体较远的脉体中通常发育金、银、铅和锌等温度较低时形成的金属矿物(图1)(Sillitoe, 2010;Dilles and John,2021).脉体为主的斑岩矿床是较为常见的斑岩矿床类型,前人推测斑岩周围网脉的形成与斑岩体的侵入、岩浆来源的热液流体的出溶以及岩浆驱动的热液系统冷却过程有关(Tosdal and Richards,2001).在角砾岩为主的斑岩矿床中,含矿角砾岩为成矿前和成矿同时形成的角砾岩,其形状由不规则状到筒状;这些角砾岩与围岩呈突变或渐变的角度接触,并且与斑岩侵入体有着密切联系(图1)(Tosdal and Richards,2001).角砾岩的基质组成为火成岩、热液硅酸盐和硫化物矿物,并且矿物的成分与斑岩矿床的蚀变分带有良好的对应关系(Tosdal and Richards,2001;Sillitoe, 2010).前人认为斑岩矿床中的角砾岩形成与火成岩、岩浆-热液和潜水岩浆作用有关(Tosdal and Richards,2001),并且距离斑岩侵入体较近的角砾岩没有明显的方向性;前人推测这与孔隙流体超压导致的岩石破裂有密切的联系(Stephens et al., 2004;刘亮明,2011).成矿后期形成的角砾岩通常含矿较少(Sillitoe, 2010).
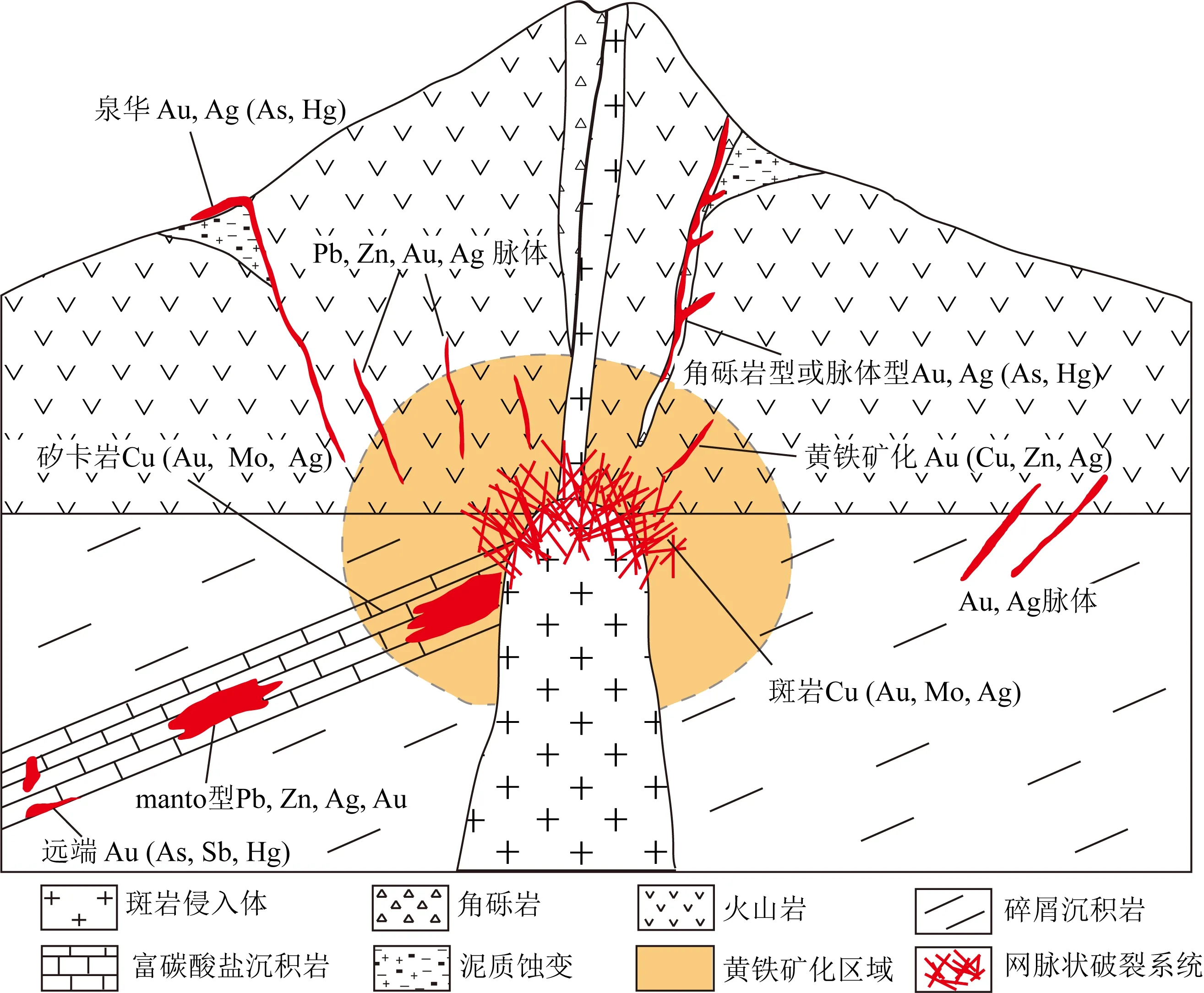
图1 斑岩矿床中斑岩侵入体顶部破裂样式和矿体类型示意图.修改自Kirkham和Sinclair (1995) Fig.1 The schematic map of fracture styles and ore types at the top of porphyry intrusion in porphyry deposits. Modified from Kirkham and Sinclair (1995)
2 THM耦合方法及控制方程
2.1 孔隙介质力学
成矿过程是一种地质时间尺度的准静态过程.因此,模型忽略了惯性力项,求解了静力平衡方程(本研究中,压应力为正,拉应力为负):
σij,j-fi=0,
(1)
其中σij(i,j=x,y,z)为总应力张量在各个方向上的分量,fi为i方向上的体力(坐标轴定义见图2a).在模型中,水平体力为0,垂直体力fy=ρmg,其中ρm为孔隙介质整体(固体颗粒骨架和孔隙流体)的平均密度,g为重力加速度(本研究中取9.81 m·s-2).孔隙介质的平均密度ρm可以表示为:
ρm=ρs(1-n)+ρfn,
(2)
其中ρs和ρf分别为固体颗粒和孔隙流体的密度,n为岩石体系的孔隙度.
本研究中的岩石材料均为线性饱和各向同性的孔隙介质材料,这种材料遵循有效应力原理(Terzaghi, 1925;Lade and Boer, 1997):
σij=σ′ij+αpδij,
(3)
其中σ′ij(i,j=x,y,z)为有效应力张量在各方向的分量,有效应力是岩石固体骨架或岩石颗粒所承受的应力;p为孔隙流体压力;δij为Kronecker delta函数(i=j,δij=1;i≠j,δij=0).α为Boit常数,α=1-K/Ks,K为孔隙介质整体的体积模量,Ks为固体骨架的体积模量.本研究中,岩石颗粒被假设为不可压缩的,Ks的值趋向于无穷,所以Boit常数α=1(Thornton and Crook, 2014;Luo et al., 2015; Simulia, 2016).
耦合温度场的孔隙介质力学本构方程可以表述为(Selvadurai and Nguyen, 1995;Atanackovic and Guran, 2000; Bai and Li, 2009):
σij=2Gεij+λθδij+αpδij+3Kβs(T-T0)δij,
(4)
其中,
(5)
εij(i,j=x,y,z)为应力张量在各个方向上的分量,u为位移;θ为体应变,εx、εy和εz分别为对应下标表示的坐标轴方向的正应变;λ和G为Lame常数,K为孔隙介质整体的体积模量,E为杨氏模量,μ为泊松比;βs为固体颗粒的热膨胀系数,T和T0分别为当前温度和参考温度(0 ℃).
本研究使用了Drucker-Prager塑性屈服准则(Drucker and Prager, 1952):
(6)
其中,
(7)
I′1为有效应力张量的第一不变量,J2为偏应力张量的第二不变量,σ′1、σ′2和σ′3分别为最大有效主应力、中间有效主应力和最小有效主应力;σ′x、σ′y和σ′z分别为相应坐标轴方向的有效正应力,在本文的模型中,σ′x、σ′y和σ′z分别对应水平有效应力σ′h、垂直有效应力σ′v和平面外法向的有效应力σ′oop(坐标轴定义见图2a);τxy、τyz和τzx为对应平面内的剪应力,在本模型的平面应变假设下,只有τxy有值,其余剪应力分量为0.φ为内摩擦角;C为岩石颗粒的内聚力.
2.2 孔隙流体压力的扩散方程(质量守恒)
本研究使用达西定律来模拟孔隙流体在岩石孔隙中的流动行为(Lewis and Schrefler, 1999; Craig, 2004; Simulia, 2016).达西定律可以表示为:
(8)

耦合了热效应的孔隙介质质量守恒方程可以表示为(Bai and Li, 2009; Selvadurai and Najari, 2017):
(9)
其中,
αT=3[nβf+(α-n)βs],
(10)
t为时间;α为Boit常数,αp和αT分别为孔隙流体压力项和温度项的耦合参数;Kf和βf分别为孔隙流体的体积模量和热膨胀系数;n为岩石体系的孔隙度.
将公式(8)和(10)代入公式(9),质量守恒方程可以表示为:
=0.
(11)
在本研究中,我们不考虑岩石颗粒和孔隙流体的可压缩性,即岩石颗粒和孔隙流体为不可压缩的,Ks和Kf均为无穷大,所以αp=0.
2.3 温度扩散方程(能量守恒)
假设岩石颗粒的温度和孔隙流体的温度相等,那么岩石颗粒的能量守恒方程和孔隙流体的能量守恒方程可以分别表示为(Nield and Bejan, 2006):
(12)

联合公式(12)和(13),可以得到孔隙介质整体的能量守恒方程(Nield and Bejan, 2006):
(14)
其中,
(15)
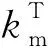
最后,我们通过联立静力平衡方程(公式(1))、本构方程(公式(4))、几何方程(公式(5)中第一个方程)、达西定律(公式(8))、质量守恒方程(公式(11))和能量守恒方程(公式(14)),来求解应力、应变、位移、孔隙流体压力和温度.在本构方程中,我们考虑了温度和孔隙流体压力的影响,在质量守恒方程中也同时考虑了温度-孔隙流体压力-应力应变的影响,在能量守恒方程中也考虑了孔隙流体热对流作用的影响.本文使用了商业有限元软件Abaqus求解上述方程组(Simulia, 2016);该方程组是耦合在一起求解的,即本文的模型是全耦合的THM模型.
3 数值模型设置
本研究使用商业有限元软件Abaqus(Simulia, 2016),构建了一个概念性的、简化的岩浆岩侵入体侵入到围岩中的二维平面应变有限元模型(图2a).该模型的时间步长由程序根据结果的收敛性自适应调整,时间步长的范围从几秒到几十年.当模型结果的收敛性较好时,时间步长较长;当模型结果的收敛性较差时,时间步长较短(Simulia, 2016).该模型长6 km,高5 km,模型中央是一个筒状的岩浆侵入体,顶部宽度约为500 m,侵入体与模型顶部表面之间的距离为1.5 km(图2a).模型的剩余部分均为围岩.
模型计算分为两步.第一步为重力平衡步,经过这一步的计算,得到用于第二步THM耦合分析的初始应力场.这一步中,我们设置水平与垂直有效应力比K0为0.5,即:
(16)
模拟了重力平衡的应力场(Luo et al.,2015).第二步为THM耦合分析计算步,在这一步中,岩浆岩侵入体的初始温度设为600 ℃,处于铜元素沉淀温度与上地壳大型岩基温度,即约550~700 ℃之间的范围内(Sillitoe, 2010;Richards, 2011);围岩的初始温度为顶部20 ℃,随着深度的增加,温度以25 ℃/km的地温梯度增加,最终在模型底部达到170 ℃(图2a).围岩的初始孔隙流体压力在顶部为1个大气压力(0.1 MPa),在其余部分为静水压加上大气压(图2a).对于边界条件,在模型顶部,其温度固定为20 ℃,其孔隙流体压力固定为1个大气压力(0.1 MPa),其法向和切向位移均自由;在模型两侧和底部,其温度由模型表面温度及地温梯度计算得到(图2a),其孔隙流体压力为静水压与大气压之和,其法向位移固定而切向位移自由.高温侵入体及其周围围岩是此模型分析的重点区域,所以模型中间区域的网格较密(图2a).
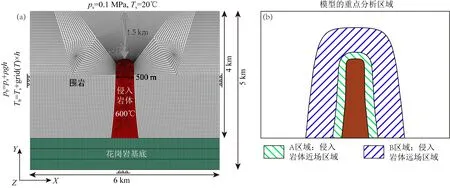
图2 (a) 高温柱状岩体侵入到围岩中的二维平面应变有限元模型的形状、网格和边界条件示意图.其中,ps为地表孔隙流体压力(大气压力),Ts为地表温度(20 ℃),grid(T)为地温梯度(25 ℃/km).(b)模型的重点分析区域.高温岩体加热围岩所产生的应力应变扰动在侵入岩体近场区域(A区域)和侵入岩体远场区域(B区域)有显著的不同,所以本研究划分了两个不同的区域便于模型结果的描述Fig.2 (a) The model shape, meshes and boundary conditions of 2D plane strain finite element model for a high temperature columnar intrusion body intruding into the wall rock. Where, ps is the surface pore pressure (atmospheric pressure), Ts is the surface temperature (20 ℃), grid(T) is the underground temperature gradient (25 ℃/km). (b) The key analysis areas of this model. The perturbations of stresses and strains induced by the high temperature intrusion body heating wall rock have distinct differences in the zone near the intrusion body (zone A) and the zone far from the intrusion body (zone B), thus, we drew two different areas for the convenience of describing model results
前人研究表明,斑岩成矿系统的热演化过程十分复杂,熔融岩浆的侵入过程以及斑岩矿床的形成过程伴随着岩浆的多次或者持续的注入(Sillitoe,2010; Owen-Smith and Ashwal, 2015; Buret et al., 2016).为了简化这种复杂的热力学过程,本模型不考虑岩浆岩侵入的大变形过程,主要模拟高温岩浆侵位完成之后侵入体加热围岩的物理场演化过程,并且在模拟持续时间内侵入岩浆始终保持600 ℃的高温,来近似高温岩浆的持续作用,直到孔隙热弹塑性模型产生一定规模的破裂系统.我们选取模型模拟1000年时的结果作为最终结果,此时破裂已经达到了一定的规模.本研究的孔隙热弹性模型与孔隙热弹塑性模型的模拟时间一致.模型所用材料参数见表1.

表1 柱状岩体侵入围岩概念模型的材料参数Table 1 The material properties for the conceptual model of columnar intrusion body intruding into the wall rock
4 模型结果
4.1 孔隙热弹性模型结果与应力应变分析
我们首先分析了弹性模型中的力学状态(图3—图7).弹性模型由于没有塑性屈服,其偏应力结果可以无限增大(Luo et al., 2012),因此,能够计算高温岩体的侵入对周围围岩应力应变的扰动.
在弹性模型结果中,高温岩体加热围岩导致的应力应变状态和扰动在靠近岩体的围岩中(或岩体与围岩的接触带中)和距离岩体较远的围岩中有明显的不同,所以本研究划分出了侵入岩体近场区域(图2b中的A区域,可简称为近场区域)和侵入岩体远场区域(图2b中的B区域,可简称为远场区域)作为两个重点分析区域,使模型结果的描述更加清晰.
4.1.1 偏应力与平均应力的变化
模型初始的I1也随深度线性增加(图3b),这与模型初始应力率一致(公式(16)).而高温岩体侵入使得I1大大增加(图3e),在侵入岩体近场区域的岩体与围岩的接触带位置,I1达到最大,约400~800 MPa(图3e).因此,高温岩体侵入导致I1在岩体与围岩的接触带位置增加了约200~600 MPa(图3h).
初始的孔隙流体压力为大气压与静水压之和,其大小是随深度线性增加的(图3c).而高温岩体侵入后,由于孔隙流体受热膨胀,岩体内部和周围围岩中产生孔隙流体超压,从而导致孔隙流体压力增加(图3f),且距离侵入岩体越近,孔压越大(图3f).在侵入岩体周围,孔压增加约25~45 MPa,且在侵入岩体2至3倍几何尺寸之外的位置,孔压的扰动就完全消散了(图3i).
4.1.2 有效主应力大小的变化


图3 孔隙热弹性模型的偏应力第二不变量总应力第一不变量I1和孔隙流体压力p的初始值大小(a—c)、最终值大小(d—f)及其变化量(g—i).灰色部分为斑岩侵入体.每个色标对应其正上方的三张图.对于I1和p的结果,挤压为正,拉张为负Fig.3 The magnitudes of the second invariant of deviatoric stress tensor the first invariant of total stress tensor (I1), and the pore pressure (p) of the thermal-poroelastic model at the initial (a—c) and final modeling states (d—f), and their magnitude perturbations (g—i). The gray part is the porphyry intrusion body. Each color bar is corresponding to the figures that are right above it. The compression is positive and the extension is negative for I1 and p
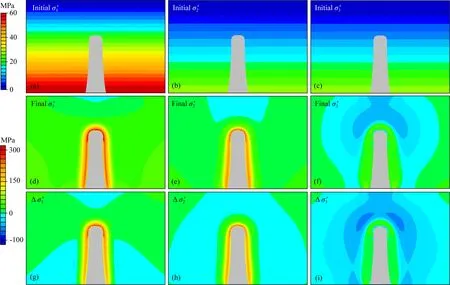
图4 孔隙热弹性模型的最大有效主应力(σ′1)、中间有效主应力(σ′2)和最小有效主应力(σ′3)的初始值大小(a—c)、最终值大小(d—f)及其变化量(g—i).灰色部分为斑岩侵入体.初始值共用上方的色标,最终值和变化量共用下方的色标.对于应力的符号,挤压为正,拉张为负Fig.4 The magnitudes of the maximum effective principal stress (σ′1), the intermediate effective principal stress (σ′2) and the minimum effective principal stress (σ′3) of the thermal-poroelastic model at the initial (a—c) and final modeling states (d—f), and their magnitude perturbations (g—i). The gray part is the porphyry intrusion body. The upper color bar is corresponding to the initial states, and the lower color bar is corresponding to the final states and the perturbations. The compression is positive and the extension is negative for stress

4.1.3 有效正应力与主应力方向
在初始时刻,垂直有效应力(σ′v)是平面外法向的有效应力(σ′oop,垂直于平面的正向有效应力)和水平有效应力(σ′h)的两倍,并且三者均随深度线性增加(公式(16);图5a—5c).高温岩浆岩体的侵入使得近场和远场区域的三个有效正应力发生了很大变化(图5d—5i).在侵入岩体近场区域(A区域,见图2b),高温岩体的侵入使得σ′oop增加了约150~300 MPa(图5g):其增加量比σ′h和σ′v的增加量都要大(比较图5g与图5h、图5i).最大有效主应力在近场区域中的方向是沿平面外法线方向的(图6a),所以靠近岩体的围岩中的最大有效主应力是σ′oop.在近场区域,σ′h仅仅在岩体顶部围岩的小范围内大幅增加了约100~200 MPa,在岩体两侧的围岩中增加量很小(图5h);而σ′v的变化则相反,在岩体顶部的围岩中增加量很小,在岩体两侧的围岩中大幅增加了约100~200 MPa(图5i).从中间有效主应力的方向图可以观察到:在侵入岩体近场区域中,中间有效主应力的方向是沿着或平行于侵入岩体边界的,即在岩体顶部接近水平方向,在岩体两侧接近垂直方向(图6b).所以,在岩体顶部,中间有效主应力近似为σ′h,而在岩体两侧,中间有效主应力近似为σ′v.与中间有效主应力方向沿着侵入体边界不同,在侵入岩体近场区域,最小有效主应力的方向是垂直于侵入岩体边界的,即在岩体顶部接近垂直方向,在岩体两侧接近水平方向(图6c).所以,在岩体顶部,最小有效主应力近似为σ′v,而在岩体两侧,最小有效主应力近似为σ′h.
在侵入岩体远场区域(B区域,见图2b),水平有效应力(σ′h)在岩体上方减小约15~45 MPa(图5h),而垂直有效应力(σ′v)在岩体两侧减小约30~60 MPa(图 5i).在侵入岩体远场区域,岩体上方的最小有效主应力近似为水平有效应力,岩体两侧的最小有效主应力近似为垂直有效应力(图6c).因此,在侵入岩体远场区域,σ′h在岩体上方的减小以及σ′v在岩体两侧的减小,使得最小主应力的变化呈现拉张状态(图4i).

图5 孔隙热弹性模型的平面外法向有效应力(σ′oop)、水平有效应力(σ′h)和垂直有效应力(σ′v)的初始值大小(a—c)、最终值大小(d—f)及其变化量(g—i).灰色部分为斑岩侵入体.初始值共用上方的色标,最终值和变化量共用下方的色标.对于应力的符号,挤压为正,拉张为负Fig.5 The magnitudes of the out-of-plane normal effective stress (σ′oop), the horizontal effective stress (σ′h) and the vertical effective stress (σ′v) of the thermal-poroelastic model at the initial (a—c) and final modeling states (d—f), and their magnitude perturbations (g—i). The gray part is the porphyry intrusion body. The upper color bar is corresponding to the initial states, and the lower color bar is corresponding to the final states and the perturbations. The compression is positive and the extension is negative for stress

图6 (a)(b)(c)分别为孔隙热弹性模型的最大有效主应力(σ′1)、中间有效主应力(σ′2)和最小有效主应力(σ′3)的方向.灰色部分为斑岩侵入体.线段的颜色代表了有效主应力分量的大小.图中的点表示该有效主应力方向是垂直于模型平面的Fig.6 (a), (b) and (c) are the directions of the maximum effective principal stress (σ′1), the intermediate effective principal stress (σ′2) and the minimum effective principal stress (σ′3) of the thermal-poroelastic model, respectively. The gray part is the porphyry intrusion body. The colors of the lines show the magnitudes of effective principal stress components. The points in this figure mean that the direction of the effective principal stress is normal to the model plane
4.1.4 温度演化与应变的结果
整体来看,侵入岩体近场区域(A区域,见图2b)的正应变以拉张应变为主,且应变值较高(图7a—7c).而在侵入岩体远场区域(B区域,见图2b),既有拉张应变也有挤压应变,但拉张应变值远大于挤压应变值(图7a—7c的色标).模型的温度在初始时刻只有侵入体温度较高(600 ℃),围岩的温度随地温梯度变化(图7d);而在模拟的最后,侵入体近场区域的围岩被加热到了较高的温度(200~500 ℃)(图7e).
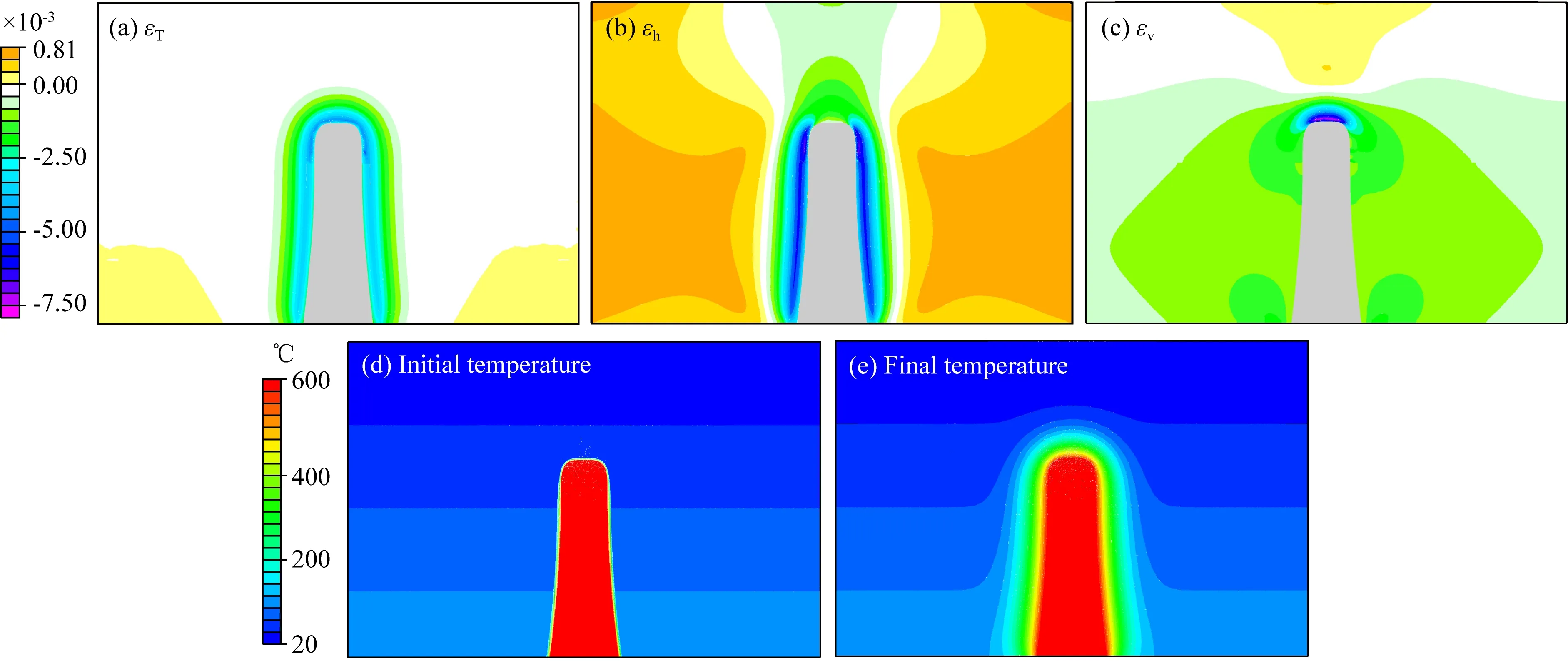
图7 孔隙热弹性模型中岩体的热作用导致的(a)围岩受热膨胀产生的应变(热应变εT)、(b)水平应变(εh)和(c)垂直应变(εv)的分布.灰色部分为斑岩侵入体.正应变和热应变以缩短(挤压)为正,伸长(拉张)为负.由于模型的平面应变假设,平面外法向的正应变为0.(d—e)孔隙热弹性模型的温度演化结果Fig.7 The distributions of (a) thermal strain (εT), (b) horizontal strain (εh) and (c) vertical strain (εv) induced by the heating effect of intrusion body in the thermal-poroelastic model. The gray part is the porphyry intrusion body. The shorten (compressive) strain is positive and the extension (tensile) strain is negative. The out-of-plane normal strain equals zero because of the plane strain hypothesis of this model. (d—e) The results of temperature evolution in the thermal-poroelastic model
高温侵入岩体加热围岩使得围岩受热膨胀(图7e),产生热应变(εT)(图7a).在侵入岩体近场区域(A区域,见图2b),距离岩体较近的围岩被加热到较高的温度(图7e),因此越靠近侵入岩体的围岩热应变(热膨胀)就越大(图7a).而在侵入岩体远场区域(B区域,见图2b),围岩没有受到高温侵入岩体的加热(图7e),所以远场区域的热应变为0(图7a).
在侵入岩体近场区域(A区域,见图2b),水平应变(εh)在岩体两侧的拉张最大(见图7b蓝色位置),可达-0.0025至-0.0075,而εh在岩体顶部的拉张较小,仅为-0.001至-0.0025(图7b).在侵入岩体远场区域(B区域,见图2b),εh只在岩体的顶部有一些拉张应变(见图7b侵入体上方的浅绿色区域),约为0至-0.00125,而在岩体的两侧呈很小的挤压应变(图7b).
在侵入岩体近场区域(A区域,见图2b),垂直应变(εv)在岩体顶部的拉张最大(见图7c蓝色位置),可达-0.0025至-0.0075,而εv在岩体两侧的拉张较小,仅为-0.001至-0.0025(图7c).在侵入岩体远场区域(B区域,见图2b),εv在岩体的顶部呈很小的挤压应变,而在岩体的两侧为拉张应变,约为-0.0004至-0.00125(见图7c侵入体两侧的浅绿色区域).
4.1.5 利用应变解释正应力的分布
对比应变的结果和三个正应力的结果可以发现,在侵入岩体近场区域,三个正应力(σ′oop、σ′h和σ′v)都是挤压应力(图5g—5i),但是应变分量(εT、εh和εv)却是拉张应变(图7a—7c);而在侵入岩体远场区域,拉张的应力又能对应拉张的应变(对比图5h和图7b,对比图5i和图7c).导致这种现象的原因是近场的围岩受热膨胀产生了拉张的热应变,但是远场的围岩没有受热膨胀,所以远场围岩会挤压并约束近场围岩的热膨胀作用,导致近场的围岩中产生了挤压的热应力,而远场的围岩由于没有被加热所以没有受到这种挤压约束作用.根据孔隙热弹性的本构方程(公式(4)),我们能更具体地看到热应变产生的挤压作用.展开公式(4),可得到平面应变孔隙热弹性(本文简称弹性模型)本构方程的各个分量:
σ′oop=λ(εh+εv)-3KεT,
σ′h=λ(εh+εv)+2Gεh-3KεT,
σ′v=λ(εh+εv)+2Gεv-3KεT,
τxy=2Gεxy,
εT=-βs(T-T0) ,
(17)
其中,εh、εv和εxy分别为水平应变、垂直应变和平面内剪应变,εT为热应变(由于规定挤压应变为正,拉张应变为负,而热膨胀为拉张应变,为了统一应变的符号,本文在热应变的表达式前加了负号).从公式(17)可以注意到,εh、εv与应力呈正相关,表明了弹性应力与应变的对应关系;而εT与应力呈负相关,表明拉张的εT会产生挤压应力.
基于上述的热应变(或热膨胀)与应力的负相关关系,根据公式(17),利用热应变(εT)、水平应变(εh)以及垂直应变(εv)的分布,可以分析和解释平面外法向有效应力(σ′oop)、水平有效应力(σ′h)和垂直有效应力(σ′v)的变化或扰动.具体分析和解释如下:
对于平面外法向有效应力(σ′oop),在侵入岩体近场区域,岩体两侧的水平应变(εh)和岩体顶部的垂直应变(εv)的拉张较大(图7b和7c),所以λ(εh+εv)这一项所产生的应力是围绕岩体的拉张应力(公式(17));靠近岩体的围岩热膨胀产生拉张的热应变(εT)(图7a),而εT导致的挤压应力的作用(-3KεT)大于λ(εh+εv)所产生的拉张应力,所以σ′oop的挤压应力增加量在近场区域中三个方向的正应力中最大(图5g)(公式(17)).
对于水平有效应力(σ′h),根据公式(17),与平面外法向有效应力(σ′oop)相比,σ′h的方程中多了2Gεh这一项,所以σ′h的扰动与σ′oop的扰动之间的差异主要受到εh的控制.在侵入岩体近场区域(A区域,见图2b)的岩体两侧,εh的拉张很大(图7b中蓝色区域),其产生的拉张应力抵消了εT产生的挤压应力(图7a与图5g),所以σ′h的增加量很小(图5h);而在近场区域的岩体顶部,εh的拉张较小(图7b),εT产生的挤压应力(图7a与图5g)只有小部分被抵消,所以σ′h有较大的挤压应力的增加(图5h中黄色和红色区域).在侵入岩体远场区域(B区域,见图2b),εT的作用较小(图7a),εh在岩体顶部为拉张应变(图7b中岩体顶部浅绿色区域),所以相比于σ′oop的扰动(图5g),σ′h在远场区域的岩体顶部有明显的拉张应力的增加(图5h中蓝色区域).
同理,对于垂直有效应力(σ′v),根据公式(17),与σ′oop相比,σ′v的方程中多了2Gεv这一项,所以σ′v的扰动与σ′oop的扰动之间的差异主要受到εv的控制.在侵入岩体近场区域(A区域,见图2b)的岩体顶部,εv的拉张很大(图7c中蓝色区域),其产生的拉张应力抵消了εT产生的挤压应力(图7a与图5g),所以σ′v的增加量很小(图5i);εv在近场区域岩体两侧的拉张较小(图7c中绿色区域),εT产生的挤压应力(图7a与图5g)只有小部分被抵消,所以σ′v有较大的挤压应力的增加(图5i中黄色和红色区域).而在侵入岩体远场区域(B区域,见图2b),εT的作用很小(图7a),εv在岩体两侧为拉张应变(图7c中绿色区域),所以相比于σ′oop的扰动(图5g),σ′v在远场区域的岩体两侧有明显的拉张应力的增加(图5i中蓝色区域).
4.2 孔隙热弹塑性模型的应力应变结果
我们在上述孔隙热弹性模型中加入了塑性,使用了Drucker-Prager塑性屈服准则,来模拟由高温岩体侵入导致的等效塑性应变(即破裂)的形成,并分析了偏应力、平均应力及孔隙流体压力对破裂形成与发育的控制影响作用(图8).孔隙热弹塑性模型结果显示,演化过程的早期(200年),破裂首先在近场区域(A区域,见图2b)侵入体与围岩的接触带中发育(图8a);演化过程的中期(500年),侵入体与围岩接触带中的破裂继续发育,而侵入体上部开始发育脉状破裂(图8b);演化过程的晚期(1000年),在侵入岩体远场区域(B区域,见图2b)中岩体顶部的侧上方发育了大中型脉状破裂系统,且破裂距离岩体中轴越远,其倾角越小:靠近岩体中轴的破裂倾角约为80°到90°,而距离岩体中轴较远处破裂倾角减小至约60°(图8c).
我们选取了新形成的破裂上的一点(图8c中点C),通过分析这一点的偏应力、平均应力、孔隙流体压力及塑性屈服准则中各项的值随时间的演化,来探讨破裂形成的力学过程(图8d).将公式(6)中的I′1展开,可得
(18)


4.3 不同侵入体温度的对比模型形成的破裂规模
在本文的孔隙热弹塑性模型中,侵入体的温度是重要的边界条件.前人的地质研究表明,在斑岩铜成矿系统中,铜元素沉淀的主要阶段的温度范围是550 ℃到350 ℃(Sillitoe, 2010).并且,湿花岗岩的固相线约为700 ℃,而上地壳的大型岩基的温度大于700 ℃(Richards, 2011).所以斑岩成矿系统的侵入体温度要大于铜元素沉淀的主要阶段的温度,还要小于上地壳岩基的温度,即约550 ℃到700 ℃.因此,我们给定的侵入体温度也处于这个范围之中.此外,为了研究侵入体的温度值对于破裂系统形成的影响,为斑岩成矿系统的侵入体温度的下限提供约束,我们设置了两个孔隙热弹塑性模型的对比模型,仅改变孔隙热弹塑性模型的侵入体温度,两个对比模型中侵入体的温度分别为500 ℃和400 ℃(图9).对比模型的演化时间和侵入体为600 ℃模型的演化时间一致(约1000年).
模型结果显示,侵入体为500 ℃时,近场区域侵入体的顶部发育了一些破裂,但是远场区域中侵入体上部只有两簇很小的破裂(图9a),远没有600 ℃模型远场区域的放射状破裂系统发育(图8c);当侵入体温度为400 ℃时,侵入体周围的破裂几乎不发育(图9b).所以,模拟结果表明,当侵入体的温度大于500 ℃时,侵入体顶部才能形成小规模的容矿破裂,这样就约束了斑岩成矿系统的破裂形成过程中侵入体温度的下限.而当侵入体温度达到600 ℃时,侵入体顶部能够形成较大规模的破裂系统(图8c).模拟结果得出的温度范围与地质实际具有一致性,为侵入体温度范围和容矿破裂形成的温度提供了物理力学的约束.

图8 (a—c)孔隙热弹塑性模型中等效塑性应变(破裂)的演化结果.灰色部分为斑岩侵入体.(d)岩体侧上部脉状破裂中一点C(图8c)的塑性屈服准则中各项及等效塑性应变随时间的变化曲线.(e)岩体顶部与围岩接触带的破裂中一点D(图8c)的塑性屈服准则中各项及等效塑性应变随时间的变化曲线Fig.8 (a—c) The result of the equivalent plastic strain evolution of the thermal-poroelastoplastic model. The gray part is the porphyry intrusion body. (d) The time-varying plots of the terms in the plastic yield criterion and the equivalent plastic strain for the point C (Fig.8c) within the vein-shaped fractures above the intrusion body. (e) The time-varying plots of the terms in the plastic yield criterion and the equivalent plastic strain for the point D (Fig.8c) within the fractures at the contact zone between the intrusion body and wall rock
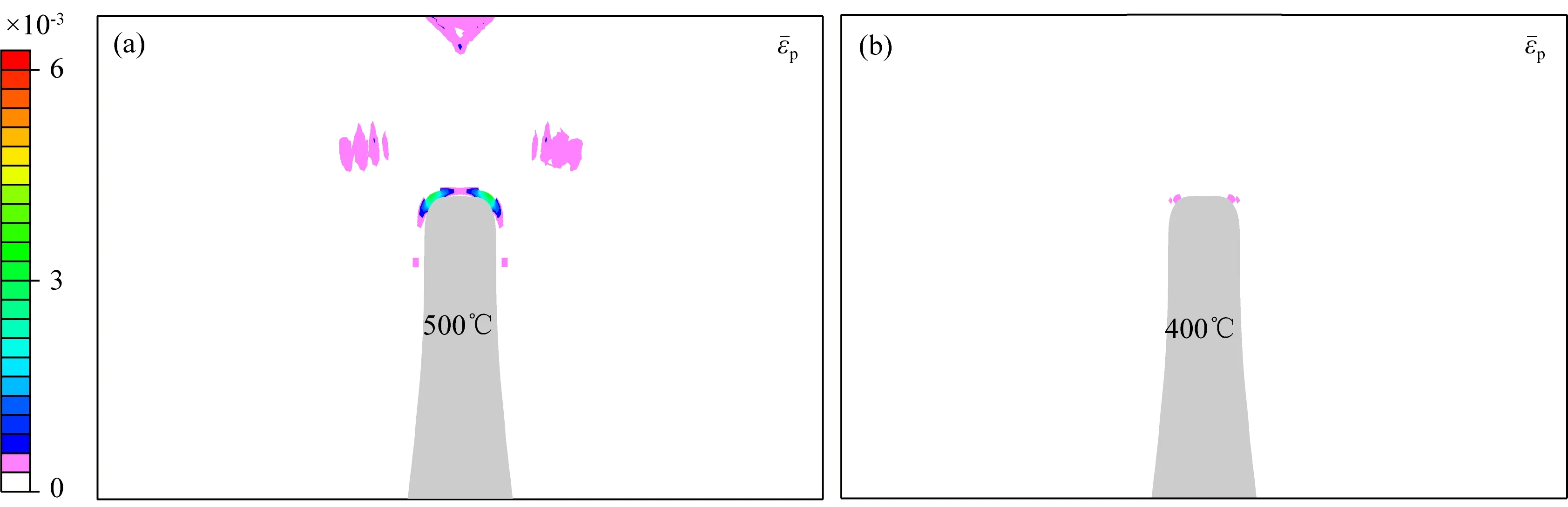
图9 (a)侵入体温度为500 ℃时,孔隙热弹塑性模型中的等效塑性应变结果.(b)侵入体温度为400 ℃时,孔隙热弹塑性模型中的等效塑性应变结果Fig.9 (a) The results of equivalent plastic strain in the thermal-poroelastoplastic model, in which the temperature of intrusion is 500 ℃. (b) The results of equivalent plastic strain in the thermal-poroelastoplastic model, in which the temperature of intrusion is 400 ℃
5 青藏甲玛斑岩矿床数值模拟
为了将本文的概念模型运用到实际矿床中,我们以青藏甲玛斑岩铜多金属矿床为例,建立了孔隙热弹塑性有限元模型,计算探讨了侵入岩体顶部围岩中的破裂样式,并与甲玛矿床实际地质观察进行了比较分析(图10).
5.1 甲玛矿床地质简述
甲玛斑岩铜多金属矿床位于特提斯—喜马拉雅成矿域的西藏冈底斯成矿带,该成矿带以中特提斯班公—怒江缝合带和新特提斯印度—雅鲁藏布缝合带为边界,在东西方向长约2000 km,在南北方向宽约500 km(杨德明等, 2001; Hou and Cook, 2009; Hou et al., 2015).前人研究表明,冈底斯成矿带经历了复杂的地质和地球动力学历史,包括雅鲁藏布新特提斯洋的俯冲-后撤-碰撞过程以及印度板块和拉萨地体的碰撞过程(Pan et al., 2012; Mao et al., 2014; Wang et al., 2015).甲玛斑岩铜多金属矿床形成于中新世印度板块与拉萨板块碰撞的后碰撞伸展阶段(约20~12 Ma),主要由四种矿体组成(图10a):(1)斑岩铜-钼矿体,赋存于斑岩侵入体内部及其周围围岩的网脉状破裂系统中,以浸染状和脉状的黄铜矿为主;(2)层状和似层状的矽卡岩铜-多金属矿体,赋存于上覆的林步宗组砂岩-板岩和下层多地沟组灰岩-大理岩的层间剥离带中;(3)角岩铜-钼±金±银矿体,主要以脉状赋存于斑岩体顶部的角岩破裂系统和节理系统中;(4)浅成热液金银矿体,主要赋存于岩体外围的破裂和闪长玢岩中(冷秋锋等, 2015; Zheng et al., 2016; 林彬等, 2019).
5.2 甲玛矿床有限元模型设置及结果
本文建立的甲玛矿床模型为二维平面应变孔隙热弹塑性有限元模型(即前文中的弹塑性模型),模型高6 km,宽8 km(图10b).模型中的地层形状与甲玛矿床的实际地层分布基本一致(图10a和10b).模型的初始条件和边界条件的设置与柱状岩体侵入围岩的概念模型一致(图10b).初始的孔隙流体压力在模型顶部为大气压(0.1 MPa),其余深度的初始孔隙流体压力为大气压力与静水压力之和;初始温度在模型顶部为室温(20 ℃),其余深度的温度按照地温梯度(25 ℃/km)增加;孔隙流体压力边界为顶部大气压,两侧和底部为大气压力与静水压力之和;温度边界为顶部室温,两侧和底部按照地温梯度增加,岩浆房的温度维持在700 ℃,也处于铜元素沉淀温度与上地壳大型岩基温度,即约550~700 ℃之间的范围(Sillitoe, 2010;Richards, 2011);位移边界条件为顶部法向和切向位移自由,两侧和底部为法向位移固定、切向位移自由(图10b).模型所用材料参数见表2.

表2 甲玛矿床模型的材料参数Table 2 The material properties for the Jiama deposit model
甲玛矿床有限元模型的结果显示,斑岩侵入体顶部形成并发育了丰富的破裂系统.从侵入岩体顶部的两个凸起开始,向外发育了倾角不同的多个破裂,岩体顶部与围岩的接触带也发育了围绕岩体边界的破裂(图10c),形成了甲玛矿床的流体通道、导矿构造及容矿空间.这些模拟的破裂带位置与甲玛矿床斑岩体顶部赋存斑岩矿体和角岩矿体的破裂系统对应很好(图10a和10c).我们的数值模拟研究从力学角度在一定程度上解释了侵入岩体顶部破裂的形成与发育,并且为地学工作者暗示了甲玛矿床的流体通道、导矿构造及容矿空间的位置及区域.

图10 (a)甲玛矿床地质剖面图,显示了不同种类的矿体在空间上的分布,以及破裂对于斑岩和角岩矿体的控制作用.修改自Zheng 等 (2016).(b)甲玛矿床二维平面应变孔隙热弹塑性有限元模型的形状、网格以及边界条件示意图.其中,ps为地表孔隙流体压力(大气压力),Ts为地表温度(20 ℃),grid(T)为地温梯度(25 ℃/km).(c)甲玛矿床模型计算得到的岩体顶部等效塑性应变的分布.灰色部分为斑岩侵入体Fig.10 (a) The geological section map of Jiama deposit, showing the spatial distributions of different ore body types and the controlling effect of fractures on the porphyry and hornfels ore bodies. Modified from Zheng et al., 2016. (b) The model shape, meshes and boundary conditions of 2D plane strain thermal-poroelastoplastic finite element model for Jiama deposit. Where, ps is the surface pore pressure (atmospheric pressure), Ts is the surface temperature (20 ℃), grid(T) is the underground temperature gradient (25 ℃/km). (c) The distribution of the equivalent plastic strain at the top of the intrusion body calculated by the Jiama deposit model. The gray part is the porphyry intrusion body
6 讨论
斑岩矿床的形成是以幔源岩浆侵入为前提的,而地幔岩浆的上涌需要板块的俯冲和碰撞等作用来形成深大断裂,为岩浆的上侵提供通道(Tosdal and Richards, 2001; Richards, 2003).因此,前人对于高温岩浆侵入体周围破裂形成力学机制的数值模拟,大多都包含挤压或者拉张的构造应力背景,从而来研究构造应力或构造运动导致的深大断裂或断层的形成与发育(Guillou-Frottier and Burov,2003; Zhang et al.,2012).但是,这些大断层的发育时间通常都为几十万年甚至几个百万年,与斑岩矿床岩体顶部或上部的破裂系统生成的时间尺度存在差异.另外,这些大断层通常切穿地壳并向上延伸至地表,与小区域的、矿田尺度的斑岩矿床岩体顶部的网脉破裂和上部的脉状破裂,在空间尺度上存在很大差异(图1).这些研究通常没有考虑岩浆侵入且加热围岩导致破裂形成的力学机理(Guillou-Frottier and Burov,2003; Zhang et al.,2012).
前人对于斑岩成矿系统的研究表明,斑岩矿床的经济矿体大多产于热液系统演化早期形成的构造和蚀变带中(Sillitoe,2010;Dilles and John,2021),且在岩浆系统到热液系统的过渡过程中,含矿热液流体能以很快的速度进入岩体周围的破裂系统中,进而析出沉淀形成矿体(Launay et al., 2018).考虑到以上因素及前人的研究,本文的模型没有包含构造应力或构造运动的作用,而是聚焦研究了高温岩体侵入后对其周围围岩的加热作用及其相关的破裂形成过程.模型结果显示,模拟到约1000年时岩体顶部就出现了具有一定规模的脉状破裂系统(图8c).这些结果表明斑岩侵入体顶部的容矿破裂系统的形成过程可能比地质上认为的时间要短得多,大约仅为千年尺度.
斑岩矿床岩体周围的容矿破裂主要分为两种,一种是岩体顶部围岩接触带中的网脉状破裂系统,这种破裂的单个破裂规模较小,但是分布密度较大,形成密集的容矿网脉,主要赋存斑岩型铜±钼矿体;另一种是岩体顶部上方具有一定规模的大中型脉体和角砾岩筒,以岩体顶部为中心,呈放射状向上方或斜上方延伸,距离斑岩侵入体较近的脉体赋存斑岩铜(金银锌)矿体或者角岩铜±钼矿体,距离侵入体较远的脉体赋存较低温度下形成的铅锌金银矿体(图1;Kirkham and Sinclair,1995;Guillou-Frottier and Burov,2003;Sillitoe,2010;Zheng et al., 2016).本文的孔隙热弹性模型模拟了高温岩体的侵入对周围围岩产生的应力应变扰动,阐述了高温侵入体加热围岩产生偏应力集中的原因(图3—图7);而在孔隙热弹塑性模型中,模拟出了岩体顶部近似放射状的大中型脉状破裂以及岩体与围岩接触带中的破裂,并且分别对两种破裂进行了应力及孔隙流体压力演化分析.这些结果表明,对于具有较高渗透率顶层的斑岩成矿系统,高温岩体侵入围岩的热作用导致的偏应力集中是侵入岩体顶部破裂系统形成的主要原因(图3d,3g,8d和8e),而孔隙流体压力对这些破裂形成也具有一定的辅助作用(图8d和8e).模型模拟的破裂结果与地质上岩体顶部的两种不同类型容矿破裂有较好的一致性,能够从地质力学的角度解释岩体顶部破裂形成机制,为斑岩矿床找矿勘探提供一定的指导作用.
本文的模型没有考虑岩浆侵入体侵入到围岩中的大变形过程,因为这一过程十分复杂,包含了多种物理力学和化学反应机制(Sillitoe,2010;Richards,2013).前人对于这种侵入过程的力学作用有过简单的研究,研究方法包括对模型底部施加不均匀的压力边界条件(Hafner,1951),以及对岩浆侵入体顶部施加向上的侵入压力(Koide and Bhattacharji,1975;Sartoris et al,1990),所得到的结果都表明岩浆侵入体的侵入压力对于岩体顶部的破裂发生和发育具有重要作用.本文没有考虑这种侵入压力的作用,而是聚焦于高温岩浆对围岩的热作用,但是能够推测,岩体侵入压力的加入会促进本研究模型中岩体顶部破裂的发生和发育.
本文通过热-流体-应力应变耦合(THM耦合)的有限元模型,重点研究了高温岩体加热围岩导致偏应力在岩体顶部集中的原因,及其导致的岩体顶部破裂系统的力学演化过程.本研究的模型并没有模拟真实的岩石开裂、流体充填、矿物析出沉淀等地质过程,因为这些过程的物理力学非常复杂,不容易模拟,模型计算也不容易收敛.本文的模型也没有考虑侵入体的流体压力、流体相分离以及流体参数随温度压力的变化等因素的影响.我们强调,本文的模型是对斑岩热液成矿系统的一阶近似,通过耦合热-流体-力学(THM耦合),来研究侵入体周围破裂形成的基本物理过程,为容矿空间的形成提供基本的力学机制解释,是向着开发更复杂、更现实的成矿过程物理模型迈出的第一步.考虑上述更现实的地质过程和因素的影响,超出了本文的研究内容,但可作为未来的研究内容和方向.
7 结论
本文开发了一套新的高温斑岩侵入体加热围岩并产生破裂的热-流体-应力应变耦合的二维平面应变有限元数值模型,研究了斑岩成矿系统顶部破裂带形成与发育的力学机制及过程.首先建立了一个简化的、概念性的柱状岩浆侵入体加热围岩的二维孔隙热弹性平面应变有限元模型,分析了高温岩浆的热作用对其围岩的应力应变扰动和破裂形成机制.近一步,在这个弹性模型中加入塑性,计算了斑岩成矿系统的应力应变,调查了岩体顶部破裂形成和发育的力学演化过程.最后,依据青藏甲玛斑岩矿床的地质、地层数据及信息,建立了更加实际的甲玛斑岩矿床成矿系统模型,计算了岩体顶部破裂的形成与发育,模拟结果与实际地质情况一致,从而为深部找矿勘探工作提供了科学指导.基于以上研究工作,本文的研究结论主要有如下几点:
(1)高温柱状侵入岩体加热了其周边围岩,对这些围岩施加了附加的变形:在侵入岩体近场区域,水平应变在侵入岩体两侧拉张较大,在侵入岩体顶部拉张较小;垂直应变在侵入岩体顶部拉张较大,在侵入岩体两侧拉张较小.在侵入岩体远场区域,岩体上部的水平应变和岩体两侧的垂直应变为拉张应变.岩体与围岩的接触带受热膨胀产生了拉张的热应变.
(2)高温柱状侵入岩体加热围岩导致了侵入岩体顶部以及侵入岩体与围岩接触带中三个主应力的增加和减小的幅度不同,从而在侵入岩体顶部以及侵入岩体与围岩接触带中形成了差应力或偏应力的集中.
(3)对于具有较高渗透率顶层的斑岩成矿系统,高温岩体侵入围岩的热作用导致的偏应力集中是侵入岩体顶部破裂系统以及侵入岩体与围岩接触带中破裂形成与发育的主要原因,而孔隙流体压力对这些破裂形成与演化也具有一定的辅助作用.
致谢感谢审稿专家的建设性意见以及编辑部的大力支持.

