化学腐蚀-冻融条件下加载岩石能量演化规律及耗散模型研究*

张淑坤，王来贵，唐楠楠

(1.枣庄学院 城市与建筑工程学院，山东 枣庄 277160;2.辽宁工程技术大学 力学与工程学院，辽宁 阜新 123000)

0 引言

季节性冻土区长期服役的隧道、水利工程、岩质边坡等岩石力学工程中，难以避免受到含有腐蚀离子地下水的冻融循环作用，严重威胁岩石力学工程的安全稳定，因此，化学腐蚀-冻融条件下加载岩石物理力学性能研究尤为必要[1-2]。

基于能量方法研究岩石破坏能够回避复杂的应力以及裂隙扩展规律分析[3-4]。国内外学者采用能量方法对于岩石在冻融循环或化学腐蚀作用开展了一系列研究。苏占东等[5]采用声发射方法研究冻融循环花岗岩抗冻性指标，认为冻融循环条件下岩石声发射能量概率密度呈现幂定律分布；刘慧等[6]对劈裂过程岩体声发射累计能量进行了分析，研究了冻融砂岩抗拉各阶段损伤演化特征；刘杰等[7]对冻融循环中低应力水平砂岩进行加卸载试验，指出岩样不可逆变形越小，岩体吸收的能量越少；康永水等[8]考虑岩体裂隙水相变的特殊性，并根据能量守恒推导出岩体冻结率的表达式；孙琦等[9]利用数字散斑方法测试冻融腐蚀复合作用下岩样的局部变形信息，结果表明在能量释放阶段，岩样随着损伤程度的加剧能量释放速度降低。

冻融或化学腐蚀下岩石力学性质的研究成果丰硕，但化学腐蚀和冻融复合作用下岩石力学性质的研究并未大量展开，特别是基于能量法建立化学腐蚀-冻融复合作用下岩石能量耗散模型的研究更为少见。本文开展化学腐蚀-冻融作用下加载岩石损伤过程中能量转化特征研究，建立与强度衰减参数、pH、冻融次数相关的能量耗散模型，以期为长期服役岩石力学工程安全稳定性评价提供理论支持。

1 试件制作及试验方法

本文中的岩样为灰白色中-细粒大理岩，取自辽西锦承线畸架山隧道。将岩样制成直径50 mm，高度100 mm标准岩石试件，如图1所示。依据岩样采集区域内地下水化学成分，配制酸性(HNO3溶液，pH为2)、中性(NaCl溶液，pH为7)及碱性(NaOH溶液，pH为12.0)腐蚀溶液，模拟自然状态地下水的化学离子浓度及pH值。采用TAW-2000型微机伺服多功能岩石试验机，对不同腐蚀冻融条件岩样开展加载试验。

图1 部分典型岩样

采用自由浸水饱和方式对岩石试样进行腐蚀浸泡28 d。冻融循环单周期时长为24 h，冻结、融化温度-20 ℃～20 ℃，冻结和融化时长均为12 h。冻融循环共分为4个等级，N分别为0，5，15，30次。

2 岩石应力-应变曲线特征分析

通过岩样单轴压缩试验，测定干燥状态下岩样峰值应力为101 MPa。化学腐蚀-冻融条件下岩石应力-应变曲线如图2所示。

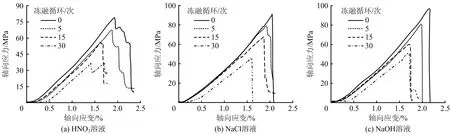
图2 化学腐蚀-冻融循环作用下应力-应变关系曲线

岩石应力-应变曲线可划分为孔隙闭合、弹性变形、塑性屈服和剪切破坏4个特征阶段。

岩石孔隙闭合阶段Ⅰ：加载初始阶段，酸性溶液应力-应变曲线下凹现象较碱性溶液更为显著。岩石孔隙闭合阶段曲线下凹程度随着冻融次数增加而不断加深。较高冻融次数及酸性溶液能促使岩石裂隙更加发育。

岩石弹性变形阶段Ⅱ：相同冻融次数下，酸性溶液腐蚀致使岩石弹性模量降低幅度最大，其次是中性溶液，碱性溶液影响最低。碱性溶液腐蚀岩石的弹性模量在冻融循环15次后才出现降低，表明岩石内部矿物结构在化学腐蚀和冻融循环作用下出现显著损伤，致使岩石弹性模量减小。

岩石塑性屈服阶段Ⅲ：岩石逐渐呈现非线性特征，开始进入塑性屈服阶段，继续加载直至岩石发生剪切破坏。在酸性溶液及高冻融循环次数下，岩石该阶段终止时对应的应力逐渐减小，而对应的应变却逐渐增大。

岩石剪切破坏阶段Ⅳ：随着冻融循环次数增加，岩石进入最后破坏阶段。高次数冻融循环条件下，酸性腐蚀岩石峰后应力降幅减小，呈现出残余强度。

选择化学腐蚀及冻融循环敏感期的因素水平，对大理岩试件开展三轴压缩试验，获得不同围压条件下(σ3=4，8，12 MPa)大理岩偏向应力-轴向应变曲线，如图3所示。

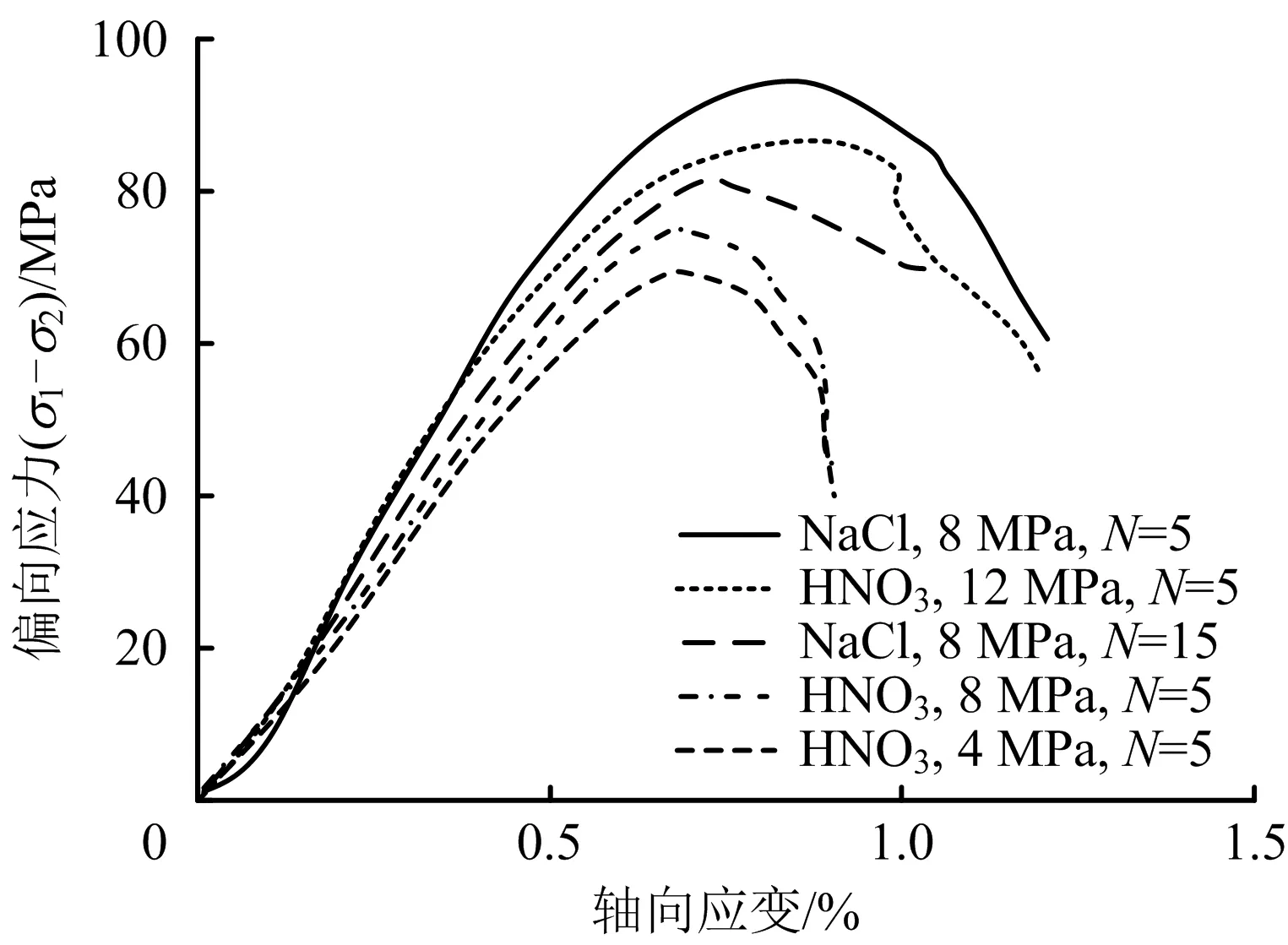
图3 不同围压下的大理岩应力-应变曲线

由图2和图3对比可知，单轴加载岩石呈现脆性破坏。三轴加载岩石软化特征更为明显，伴有体积扩容现象。原因在于，围压限定了岩石侧向变形，延缓峰后强度下降，围压越大，延缓越明显。该试验结果为后续岩石能量耗散模型建立提供数据支持。

3 化学腐蚀-冻融条件下岩石能量耗散模型研究

3.1 岩石能量耗散基本原理

岩石在受荷破坏过程中发生4种能量间的相互转化：能量输入、能量积聚、能量耗散及能量释放[10-12]。加载过程中，岩石吸收的总能量一部分以弹性应变能形式储存于岩石内部，另一部分以岩石损伤劣化形式消耗，与外界发生热交换等形式释放能量可忽略。

试验仅以单轴应力-应变曲线为研究对象，总能量、弹性应变能及耗散能可表示为式(1)：

(1)

式中：E0为初始弹性模量，MPa；σ1i为岩石破坏过程中每一点的应力值，MPa；Ue为弹性应变能，kJ/m3；Ud为耗散能，kJ/m3；U为总能量，kJ/m3；σ1，ε1分别为主应力方向上的总应力和总应变，MPa。

3.2 基于能量理论岩石损伤特征分析

基于岩石单轴压缩应力-应变试验数据，绘制冻融腐蚀岩样能量变化曲线，如图4所示。

由图4(a)，图4(d)和图4(g)可知，总能量U变化曲线在前期均呈现上凹型，斜率变化大，能量吸收快，后期曲线斜率趋于恒定。相同冻融循环次数下岩石吸收的能量随着轴向应变的增大而增加，碱性溶液下岩石试件吸收的能量总是低于酸性溶液。当冻融循环5次时，碱性溶液中岩石所吸收的总能量低于其他冻融条件下的岩石。这主要是由于在碱性溶液中,岩石内部CaO，MgO等无机矿物成分逐渐转化为Ca(OH)2和Mg(OH)2，并填充于岩石的孔隙和裂缝中，抑制了岩石损伤劣化发展，而冻融循环加快岩石裂隙和孔隙扩展速度，同时也促进了Ca(OH)2，Mg(OH)2等化学物质向岩石内部迁移。因此，在碱性溶液中，较低次数的冻融循环短期内提高了岩石吸收外界能量的能力。

由图4(b)，图4(c)，图4(e)，图4(f)，图4(h)和图4(i)中弹性能应变能Ue和耗散能Ud变化曲线可知，同一化学腐蚀液条件下，岩石弹性应变能曲线呈现为先增后减的非线性关系，而耗散能曲线则呈现先缓增后陡增的趋势。随着冻融循环次数的增加，弹性应变能吸收与释放逐渐减小，碱性溶液中岩石的能量变化总是低于酸性溶液。

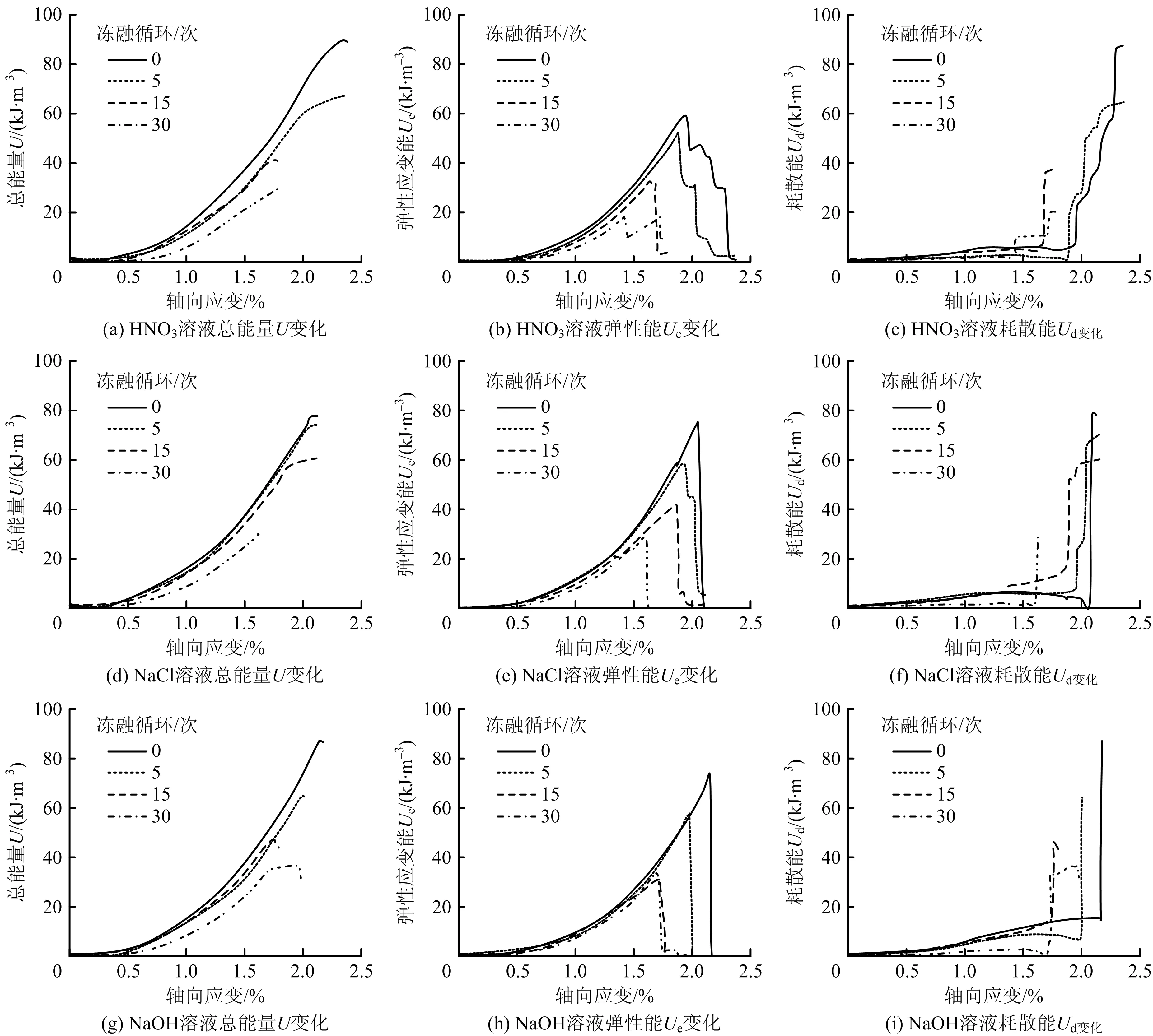
图4 不同试验条件下大理岩能量转化关系

3.3 化学腐蚀-冻融条件下岩石能量耗散模型的建立与验证

基于能量损伤理论描述岩石的损伤破坏过程，依据图3中HNO3溶液中冻融循环3次的岩石三轴试验数据，确定岩石强度参数。通过FLAC3D内嵌语言FISH，引入并定义pH值及冻融循环次数为变量，构建腐蚀冻融复合作用下岩石能量耗散模型，其他腐蚀溶液冻融条件下岩石能量耗散模型建立过程类同。

3.3.1 基于FLAC3D中FISH语言的能量耗散模型开发

FLAC3D采用显示差分算法，在给定t时刻应力值σiI和Δt时间步总应变增量Δεi，进而求解t+Δt时刻应力状态ΔσiN(i=1,2,3)，如式(2)[13]所示：

(2)

λs，Nφ计算如式(3)所示：

(3)

式中：φ为内摩擦角，(°)；ψ为剪胀角(°)；α1，α2均为岩石材料常数。

根据FLAC3D应变软化模型屈服准则，岩石材料剪切破坏面上应力满足式(4)：

(4)

式中：c为黏聚力，kPa。

在FLAC3D数值计算模型中，式(4)为岩石损伤破坏失稳判定条件。同时，模拟计算单元体内部能量时，需引入指针函数捕获单元t时刻内应力ΔσiI，以及Δt时步内的应变增量Δεi，还包括t+Δt时刻单元体应力分量ΔσiN。计算求解Δt时步内单元体平均应力分量Δσi′，进而求解单元体总输入能量及对应的积蓄弹性能和外部耗散能。

如图5[13]所示，采用单元t时刻应力ΔσiI和t+Δt时刻应力ΔσiN的平均值表征Δt时间步单元应力σi′，如式(5)所示：

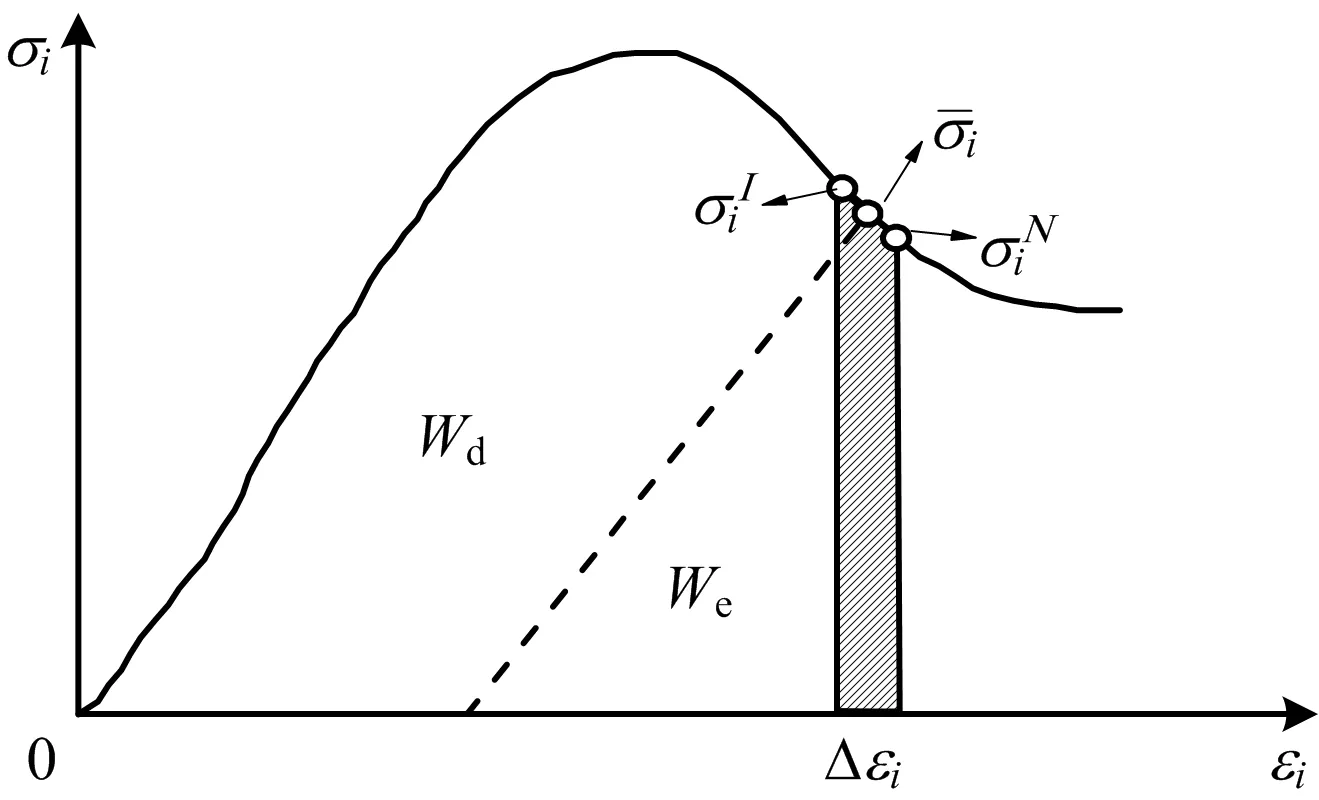
图5 单元能量计算简图

(5)

假设t时刻对应第n循环，t+Δt时刻对应第n+1循环，则第n+1循环内总能量增量可表示为式(6)：

ΔWZ=∑σi′Δεi，(i=1，2，3)

(6)

在第n个循环到第n+1循环运算的计算含义为：岩体承受荷载作用时，某一运算时步内单元网格应力-应变行为的差分运算。t+Δt时刻单元总能量等于n+1循环总能量的累积能量和，如式(7)所示：

(7)

单元体内部积蓄弹性应变能可由式(8)计算：

(8)

式中：We为单元体内部积蓄弹性应变能，kJ/m3。

则单元体能量耗散模型如式(9)所示：

(9)

式中：Wd为单元体内部耗散能，kJ/m3；E为弹性模量，MPa。

3.3.2 基于M-C准则岩石损伤衰减参数确定

针对所建立的模型引入强度参数损伤因子。引入塑性软化区内摩擦角与内黏聚力2个强度参数为损伤因子，表征化学腐蚀及冻融循环双场作用下的岩石损伤[13]。

在σ1-σ3坐标平面内，如式(10)所示：

(10)

式中：σc为峰值单轴抗压强度，MPa；θc为峰值强度所对应的岩石破断角，(°)；σΔεi为与Δεi相对应的岩石抗压强度，MPa；θΔεi为与Δεi相对应的岩石破断角，(°)。

也可以表示为式(11)：

(11)

对比式(10)和式(11)可知存在式(12)的关系：

(12)

式中：φc，φΔεi分别为峰值强度和Δεi对应的内摩擦角，(°)；Cc，CΔεi分别为峰值强度和Δεi对应的黏聚力，MPa。

基于应力-应变曲线，结合式(12)可计算求解出不同Δεi所对应的岩石强度参数，如当Δεi为残余强度应变时，绘制不同围压下岩石残余强度回归方程直线，可获得岩石残余强度下的内摩擦角φw与黏聚力cw。

依据以上方法，结合HNO3溶液中冻融循环3次的岩样全应力-应变曲线，用图解法可确定不同Δεi对应下的的σi[13]，并绘制相应的主应力-围压拟合直线，进而利用式(12)中的左式计算得到此时岩样的内摩擦角φΔεi以及黏聚力cΔεi，计算结果见表1。

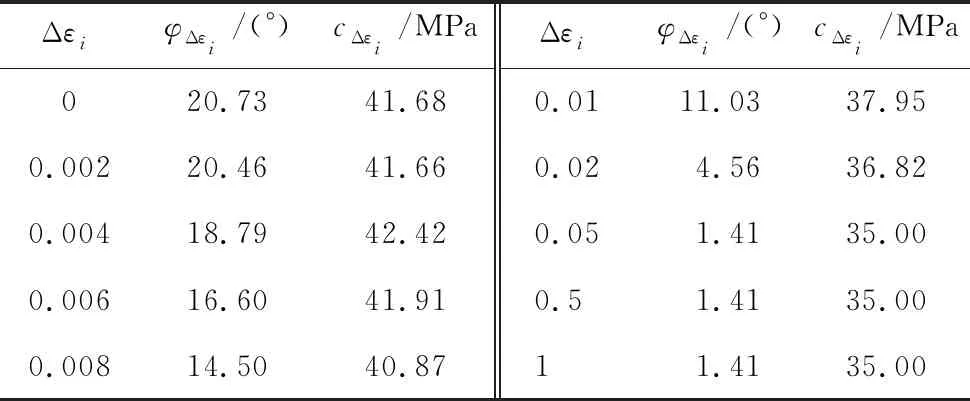
表1 大理岩石不同阶段强度参数

根据腐蚀与冻融循环条件下岩石峰值强度数据，拟合可得强度与pH和冻融循环次数间的关系，如式(13)[14]所示：

SσN=S0e-[0.000 23(pH)+0.009 8]N

(13)

式中，SσN为经历N次冻融循环后岩石单轴抗压强度，MPa；S0为岩石干燥状态下单轴抗压强度，MPa。

根据表1中计算结果，将式(13)引入式(9)建立与pH、冻融循环次数相关的岩石能量耗散模型。

3.3.3 化学腐蚀-冻融条件下岩石能量耗散模型的求解与验证

二次开发FLAC3D，写入岩石能量耗散模型，流程如图6所示。

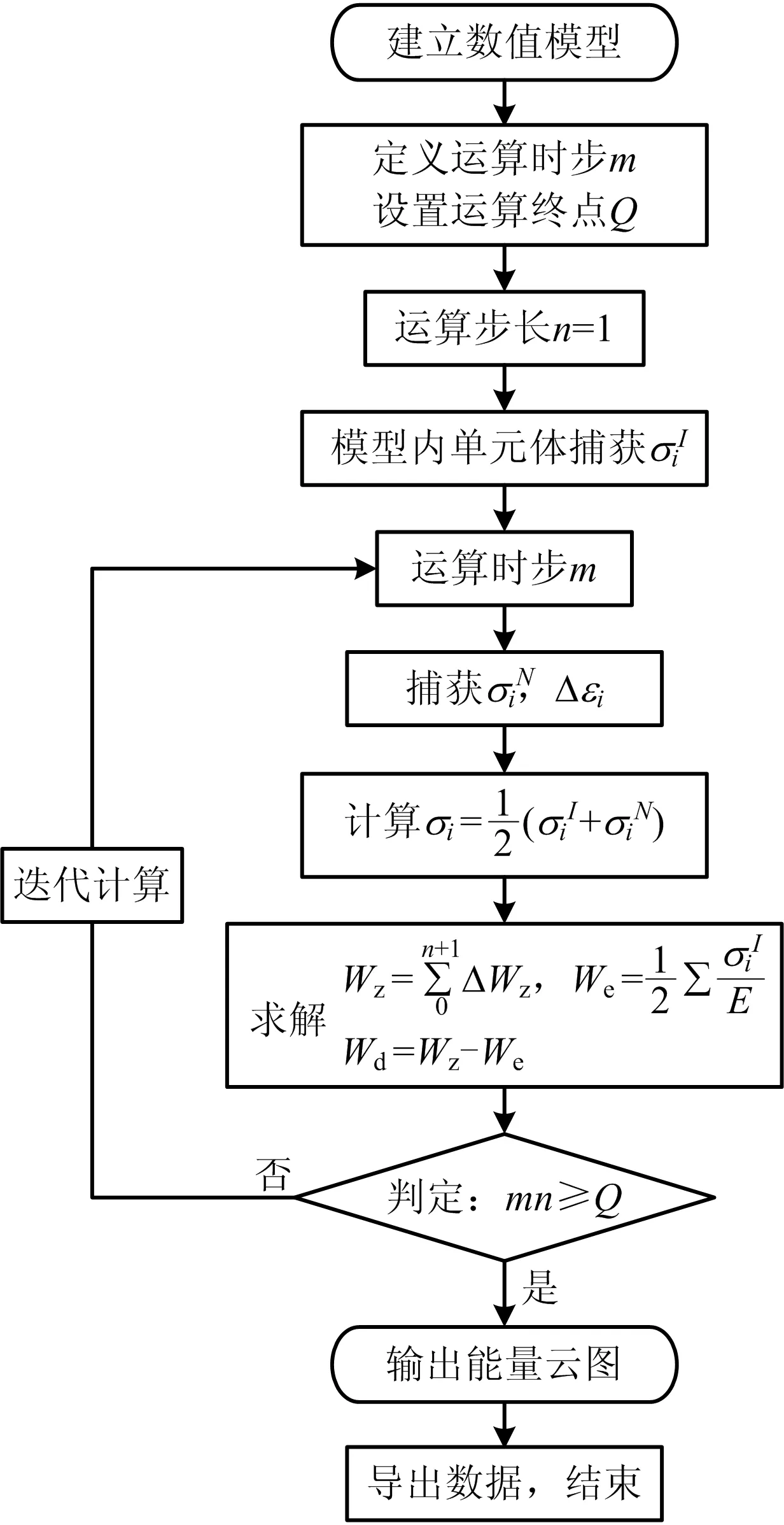
图6 单元能量计算流程

将建立模型网格化，进行网格单元体编号，m为单循环运算时步，Q为运算终止条件。在进行模型运算前，将各个单元体的初始应力σiI检索并存档，随后开始进行第1次循环计算，经历m运算时步后，检索此时单元体的应力值σiN与应变增量Δεi，并求解单元体能量，将求解计算值复核运算终点Q[15]。运算达到终点Q，能量值自动赋予单元体，若不能达到终点，则继续重复上一循环，直至所有单元体均满足运算终止条件Q，输出能量云图、导出计算结果。

采用图6中计算流程，结合HNO3溶液中冻融循环3次的岩样试验原始数据，将围压分别为4，8，12 MPa的岩石加载计算结果与试验曲线进行校核验证，如图7所示。

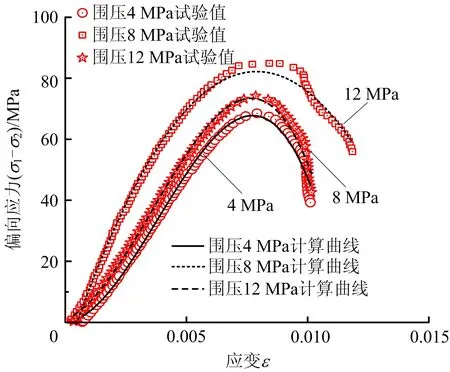
图7 应力-应变曲线校验

由图7可知，模拟计算曲线与试验曲线较为一致，能够较为准确地描述岩石各阶段力学特征。相比高围压条件下，低围压条件下的岩石峰后能量曲线模拟计算拟合准确程度更高。

可以基于该能量模型展开进一步的研究，绘制岩石耗散能模拟计算曲线与耗散能试验曲线对比如图8所示。

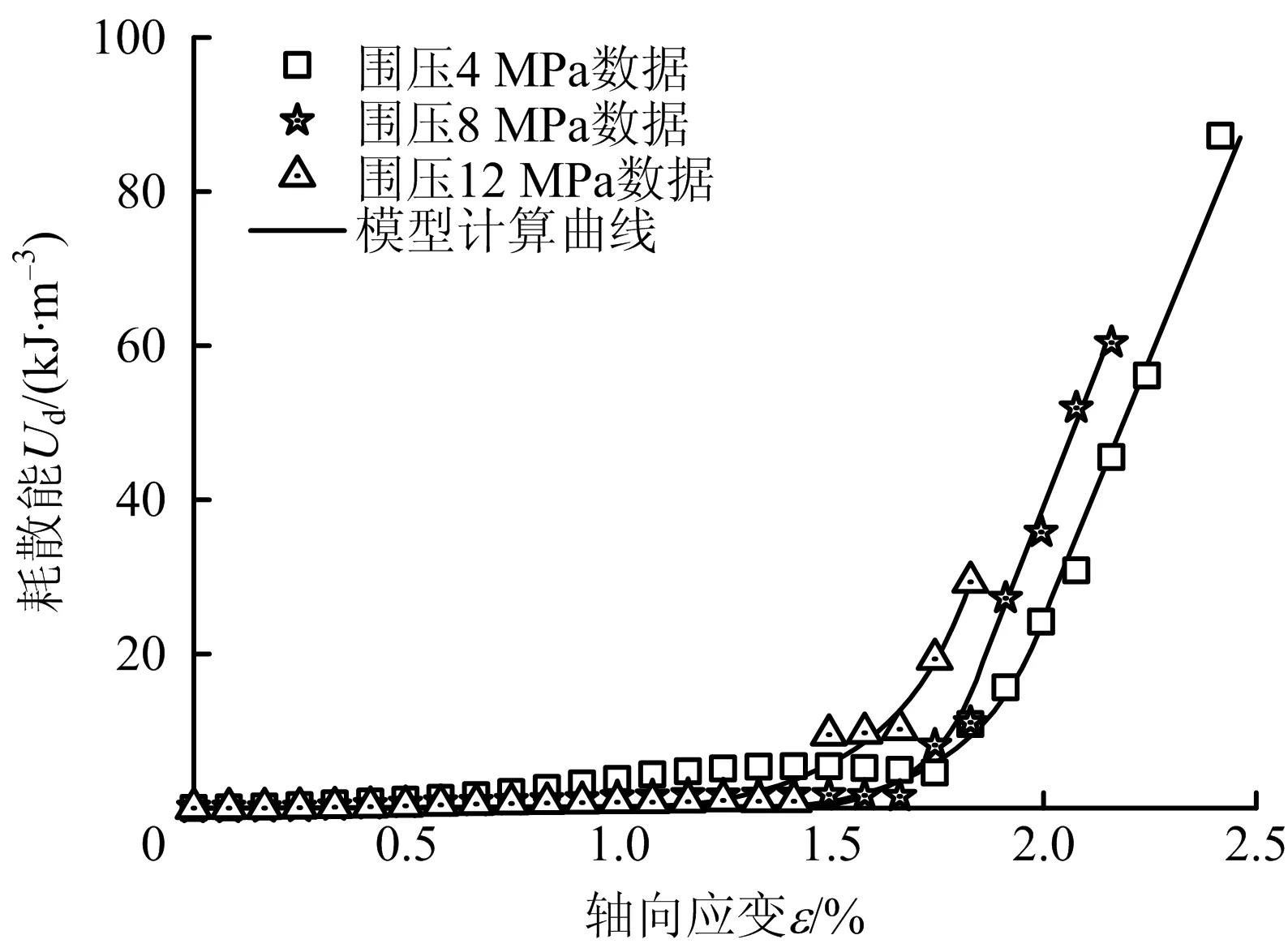
图8 岩石能量耗散模型验证

图8中能量耗散模拟曲线与试验曲线同样较为吻合。峰前岩石能量释放率很低，模拟曲线则接近于0，原因是模拟过程中未能考虑岩石内部结构压密的能量耗散。岩石试验曲线的峰后累积轴向应变达到峰前20%时，岩石耗散能指数型增长，进入破坏阶段后，耗散能更是呈现直线型陡增，进入残余强度阶段。该阶段数值模拟与试验曲线高度一致。因此，所建立的能量耗散模型对于岩石峰后阶段耗散能具有较高的准确性，能较好地模拟岩石峰后能量转化特征。

4 结论

1)腐蚀和冻融作用下，腐蚀孔隙为水增加了入渗通道使冻胀效应增加，冻胀导致裂隙同时也为溶液腐蚀形成了贯穿的通道，加剧了岩石内部结构的崩解与裂隙扩展贯通。与NaOH融合和NaCl溶液相比，HNO3溶液对岩石的化学腐蚀程度最高。

2)单轴压缩应力-应变曲线表明，相同冻融次数下的HNO3溶液腐蚀致使岩石弹性模量降低幅度最大，NaCl溶液次之，影响最低为NaOH溶液。NaOH溶液腐蚀岩石在冻融循环达15次后，对应弹性模量才开始降低。

3)腐蚀岩样弹性应变能的吸收和耗散能的释放，随着冻融循环次数的增大而减小。建立化学腐蚀-冻融条件下大理岩能量耗散模型，计算精度较好。