基于机器学习的城市用水量预测模型研究
朱铭江,裘 娅,张祖鹏
(1.长兴县水利局,浙江 长兴 313100;2.永康市水务局,浙江 永康 321300)
城市用水包括城市居民生活用水、服务业用水和重要工业用水。保障城市供水安全是支撑城市长期稳定发展的重要基础。城市用水量大,天然降水量随机性强,导致降水偏枯的年份城市供水安全保障压力较大,对城市供水调度工作提出了较高要求。准确掌握城市未来时段的用水量需求,是制定精准高效的城市供水调度方案的关键,是城市供水调度工作决策部署的基础和前提。
目前,基于机器学习算法的数据挖掘方式在城市用水量预测领域中被广泛应用:朱智伟[1]等采用ARIMA 模型、灰色GM(1,1)模型和多元线性回归分析等3 种模型,建立以污水处理量、生产总值、总人口等5 种因子为自变量的郑州市年度用水量预测模型;李彦彬等[2]采用基于HP 滤波分解的GM-LSSVR 预测模型,建立以总人口、平均气温、绿化率等8 种因子为自变量的郑州市年度用水量预测模型;吴永强等[3]采用由5 个GM(1,1)模型组成的灰色动态模型群,建立以历史上不同周期用水量作为自变量的衡水市年用水量预测模型;白鹏等[4]采用年增长率法、自回归模型法和灰色神经网络法,建立以历史用水量作为自变量的京津冀三地年用水量预测模型;陈庄等[5]采用基于MIC-XGBoost 的混合预测模型,建立以温度、季节、节假日等4 种因子作为自变量的月尺度城市用水量预测模型;姚俊良等[6]采用神经网络算法,建立以前1 d 用水量和前8 h 用水量为自变量的城市日用水量预测模型;刘志壮等[7]采用一种基于小波分解与随机森林模型、ARMA 模型结合的短期用水量预测方法,构建以气象数据、时间信息、节假日信息等因子作为自变量的城市短期日用水量预测模型。
总结目前围绕城市用水量预测的研究成果可知,预测模型采用的理论方法已较为成熟,但是多数研究的预测模型采用的自变量数据缺乏实时监测条件,需要通过定期调查分析的手段获取,导致只能对年尺度用水量进行预测。随着浙江省水利数字化改革的深入推进,运用数字化手段赋能城市供水调度工作对于提升城市供水安全保障水平具有重要作用。基于此背景,本次选择具有在线实时监测条件的城市水厂取水量数据作为自变量,采用基于粒子群算法优化的支持向量机方法挖掘城市水厂历史取水量规律,建立月尺度城市用水量预测模型,为城市供水数字化调度管理提供技术支撑。
1 研究方法
1.1 支持向量机模型
支持向量机(Support Vector Regression,SVR)作为常用的机器学习方法被广泛应用于时间序列预测,能很好地处理小样本数据、非线性及时间序列等问题,且具有较强的泛化能力[8]。SVR 方法主要思想:利用非线性映射将样本集从低维空间映射到高维空间,再从高维空间中构建回归方程。
假设给定样本集S=,x为输入向量,xi∈Rn,y为相应的输出向量,yi∈R。其非线性映射可定义为:

式中:x为输入数据;φ(x)为非线性映射函数;ω为权重;b为截距。根据结构风险最小化原则,f(x) 可等效于求解优化问题,即:
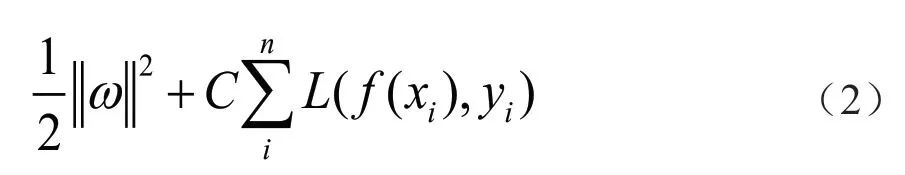
式中:L为损失函数;C为惩罚因子,是调节样本回归模型的复杂性与样本拟合精度的因子,C越大,则越重视离群点。通过引入松弛变量和来纠正不规则的因子,此时可得:
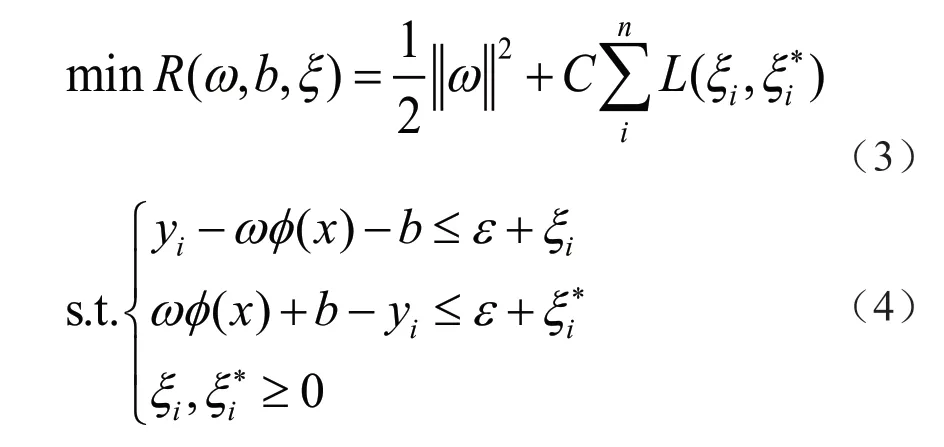
式中:ε为不敏感损失因子(允许的最大误差),ε>0。将回归问题转换为求取目标函数的最小化问题,利用对偶原理,同时引入拉格朗日乘法算子,可转换为:
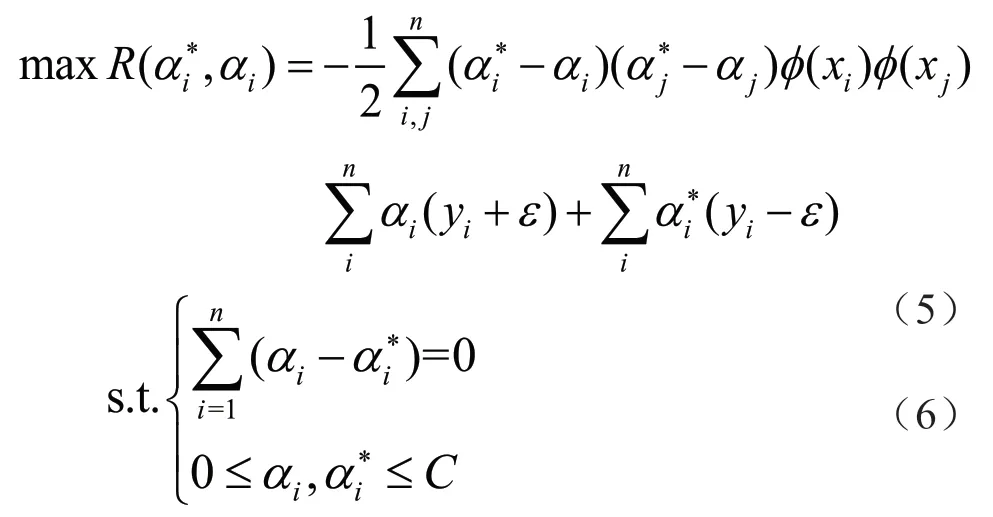
式中:αi和αi*为拉格朗日乘数。根据Mercer定理法则,求解上述凸二次规划问题并获得非线性映射SVR 表达式为:
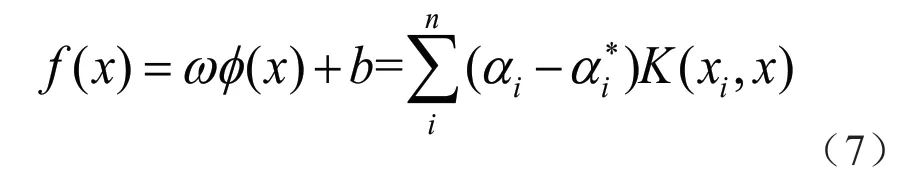
式中:K(xi,x)=φ(xi)φ(xj)为核函数。径向基函数(Radial Basis Function,RBF)用途广泛,也是被广大学者所采用的核函数,因此选取RBF核函数,其可定义为:

式中:γ为核参数,。
1.2 粒子群优化支持向量机
惩罚因子C和核参数γ直接决定了SVR 方法的准确性,为了提高SVR 模型的预测精度,需要对这两个参数进行寻优选取[9]。因此,选取粒子群优化算法(Particle Swarm optimization,PSO)对惩罚因子C和核函数参数g、p进行寻优[10]。
粒子群优化算法,其基本思想:在D维目标搜索空间,有m个例子由3 个向量表示,第i个粒子当前位置可表示为xi=(xi1,xi2,L,xiD)T,速度为vi=(vi1,vi2,L,viD)T;pi=(pi1,pi2,L,piD)T表示第i个粒子个体极值点位置;pg=(pg1,pg2,L,pgD)T表示整个种群全局极值点位置。粒子根据个体极值点和全局极值点重新确定本身位置和速度,速度和位置更新如下:
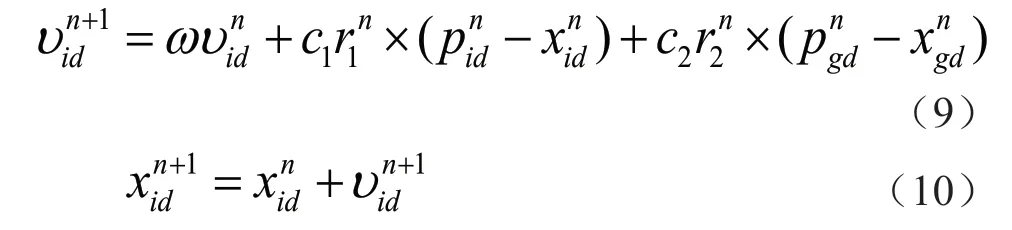
位置更新公式由3 部分组成:量部分、个体认知部分及社会认知。
粒子群算法优化支持向量机的具体流程图[11]如下:
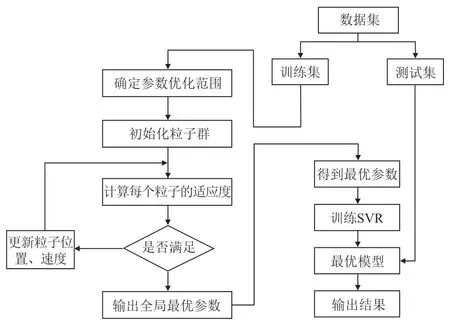
图1 PSO-SVR 模型计算流程图
2 基础数据
长兴县地处三省交界、长三角一体化核心区域,是上海经济区的交通枢纽,雄踞江苏、浙江、安徽三省结合部。长兴县水陆交通便利,距湖州市20 km,距上海市180 km,距杭州市中心90 km。航道通航里程262 km,船只可达湖州、杭州、上海、苏州等地,为长兴物流畅通和经济发展提供优越的便利条件。
长兴县城市用水主要由长兴水务公司供水,取水水源主要为合溪水库。目前,长兴水务公司取水量具有在线实时监测数据,数据采集频率为15min/次。本次研究收集长兴水务公司2013—2021 年取水实时监测数据,并统计至逐月尺度,结果见图2。
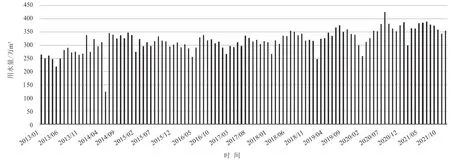
图2 长兴水务公司2013—2021 年逐月用水量图
3 模型构建
3.1 预测因子筛选
预测因子是指用水量预测模型的自变量参数。由于本次长兴县城市用水量预测模型构建采用的基础数据为具备在线实时监测条件的逐时段用水量,因此自变量参数也需在时段用水量范围内筛选。考虑与预测输出结果(时段用水量)具有相关关系的变量为前期(前1 月,前2 月,前3 月,……,前n月)用水量,采用相关系数法[12]筛选最终预测因子,相关系数是衡量变量之间线性相关程度的指标,其表达式为:
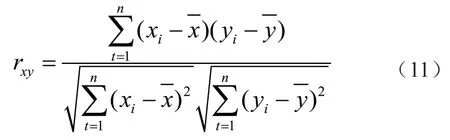
式中:xi(i=1,2,...,n)为变量x的系列值;yi(i=1,2,...,n)为变量y与x相对应的系列值;分别为x、y的平均值。相关系数有正有负,即正负相关。这里按照绝对值的大小进行衡量,不管正负相关,只要其相关系数的绝对值较大,就说明两者有较好的相关性。
基于长兴水务公司2013—2021 年逐月用水量数据,采用相关系数法筛选长兴县城市用水量预测模型预测因子,结果见表1。其中选择相关系数在0.5 以上的预测因子作为最终输入因子。
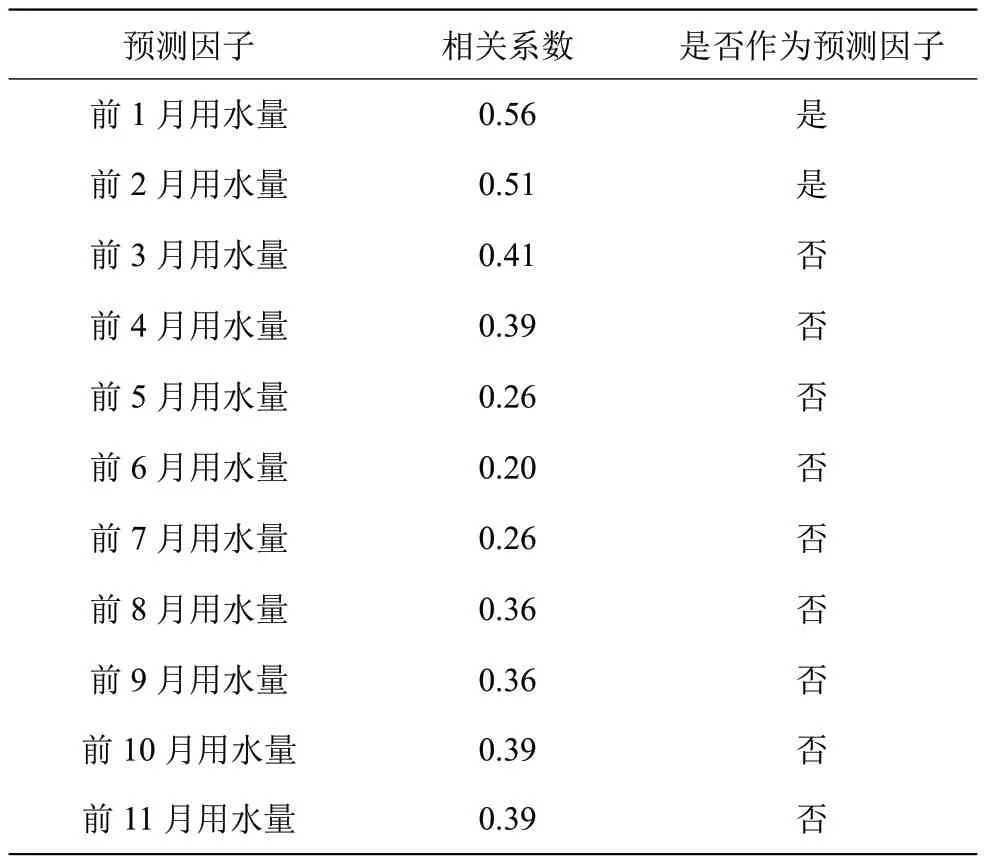
表1 长兴县城市用水量预测模型预测因子表
3.2 预测模型构建
以长兴水务公司2013 年3 月—2021 年12 月用水量作为长兴县城市用水量预测模型输出,以预测时段前1 月、前2 月用水量作为模型输入,采用支持向量机模型构建城市用水量预测模型。其中支持向量机模型惩罚系数c、核函数参数g、p采用粒子群算法进行优化。将80%的基础数据序列用于模型训练,20%的基础数据序列用于模型验证。经训练和验证的用水量预测模型相关参数见表2,模型训练期和验证期预测结果见图3~4。
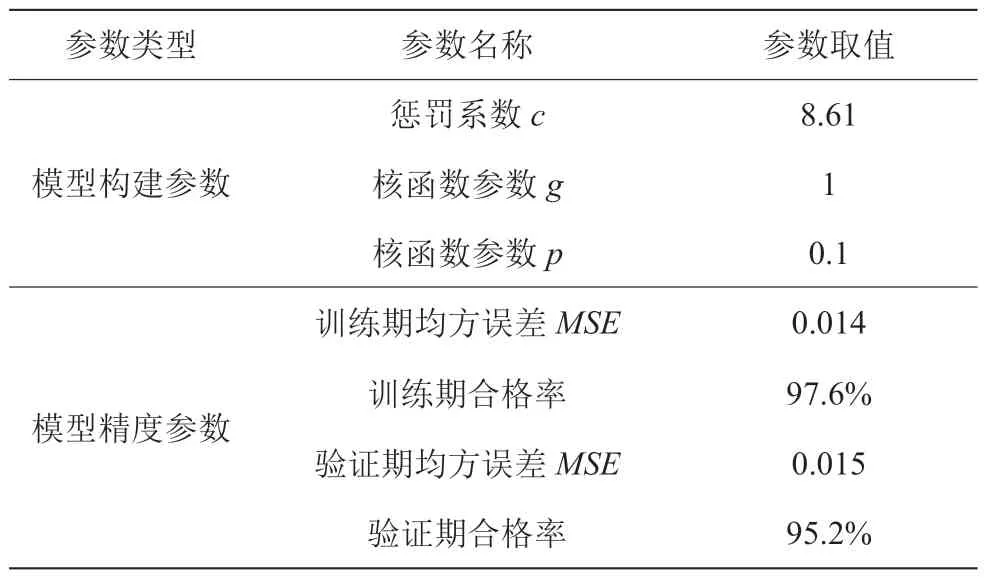
表2 长兴县城市用水量预测模型参数表

图3 长兴县城市用水量预测模型训练期预测结果图
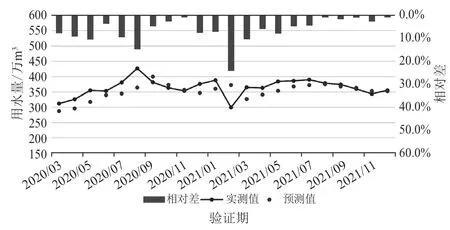
图4 长兴县城市用水量预测模型验证期预测结果图
4 结果分析
4.1 模型精度分析
根据长兴县城市用水量预测模型构建结果可知:模型在训练期及验证期精度均较高,其中训练期模型预测结果合格率达到97.6%,均方误差为0.014;验证期模型精度稍有下降,但合格率也达到95.2%,均方误差为0.015,均满足实际管理需求。
4.2 模型性能分析
提取粒子群算法对支持向量机模型惩罚系数c、核函数参数g、p等参数的优化过程(见图5)。由此可知,采用粒子群算法优化模型参数可使支持向量机模型适应度快速达到最优,是提升模型参数优化效率的有效方法。
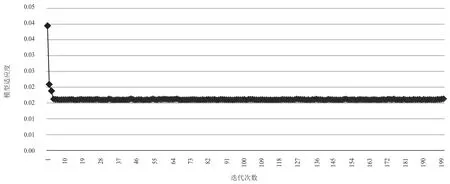
图5 粒子群优化的支持向量机模型适应度进化过程图
5 结语
以长兴县水务公司2013—2021 年逐月用水量数据为基础,通过长兴县城市用水量预测模型构建的实例研究可知:
(1)长兴县城市用水量预测模型筛选的预测因子为预测时段前1 月、前2 月用水量;模型训练期和验证期预测精度较高,可以满足实际应用需求;
(2)以支持向量机模型为代表的机器学习方法,通过挖掘用水量大数据内在规律,在城市用水量预测方面精度较高,具有较好适用性,可以为水利数字化改革提供高效的用水量预测模型组件。
——浙江省长兴县第四小学青年教师施燕燕

