基于Plackett-Burman 试验设计的颗粒流模型细观参数敏感性分析

宋 彧，冷国杰，杨安玉

（1.浙江国贸集团东方机电工程股份有限公司，浙江 杭州 310000；2.南京水利科学研究院，江苏 南京 210024；3.水利部农村电气化研究所，浙江 杭州 310012）

1 问题的提出

天然岩土材料在漫长的地质过程中，形成了异常复杂的结构，成分、大小不一的矿物颗粒以不同的方式结合在一起，聚集为团粒，团粒再堆积起来形成岩土材料，期间由于外部作用，形成节理裂隙，从而使岩土材料具有结构性。岩土材料的结构性带来岩土问题的非线性、复杂性[1]。颗粒流法[2-6]是研究岩土体材料机理特征的一种有效的数值分析方法。

当前，常用的颗粒流模拟程序PFC 中，数值模型的宏观基本物理特性无法通过直接赋值的形式实现，只能对构成模型颗粒的几何特性及颗粒间接触的细观力学参数进行赋值[7-8]。且必须通过大量试算，标定出细观参数，才能使数值模型表现出所需宏观物理特征。

文章采用PFC2D 程序建立颗粒流接触黏结模型进行单轴压缩模拟，并通过Plackett-Burman 设计获得模型各细观参数的敏感性响应，筛选出影响各项宏观力学特性的主要细观参数因子，提高颗粒流模型细观参数标定的便捷性。

2 Plackett-Burman 试验设计

Plackett-Burman（P-B）试验设计是由R.L.Plackett和J.P.Burman[9]于1946 年提出。是一种基于非完全平衡块原理近饱和的2 水平试验设计方法，通过N次实验至多可以研究（N-1）个变量，其中每个变量取高、低2 个水平。P-B 试验设计能够确定显著影响因子，从而在众多的变量因素中快速有效地筛选出最为重要的几个因素[10]。

P-B 试验设计采用线性函数筛选得出重要因素，不考虑相互影响，其中，函数方程为：

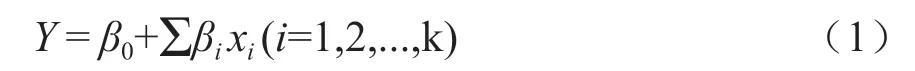
式中：Y为响应函数值，Xi为设计函数值。β0和βi为回归系数，通过回归系数的显著水平P值来反映Xi对Y的影响程度。

3 基于Plackett-Burman 试验设计的模型计算

3.1 数值模型建立

研究数值模型宏观物理特征对于细观参数的敏感性响应，无需对应于某一真实的岩石试件。数值模型的宏观物理特征参数为弹性模量、单轴抗压强度及泊松比。综合考虑众多文献资料，建立一颗粒流接触黏结模型，模型初始参数取值见表1。

表1 数值模型的细观参数表

生成的初始模型见图1，模型尺寸18.58 mm×49.80 mm，共生成颗粒1 079 个。建立上下左右4 面墙（Wall），对模型进行边界约束。移动上下墙对模型施加轴压，通过对模型进行数值单轴压缩试验可获取模型的宏观物理特征参数。

图1 颗粒流数值模型图

3.2 单因子试验确定因子水平

3.2.1 颗粒接触模量

对颗粒接触模量这一细观参数进行单因子试验，颗粒接触模量分别取10，20，30，40，50，60，70 GPa，其余参数与初始模型参数相同。建立7 个模型分别进行数值模拟得到应力—应变曲线（见图2）。

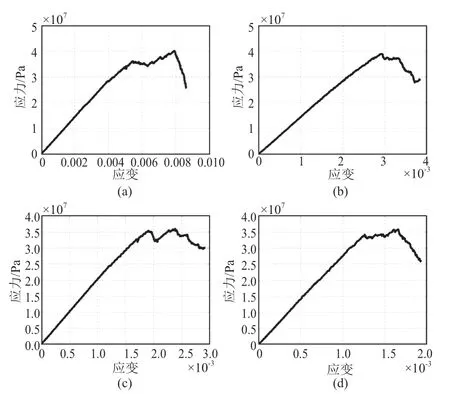
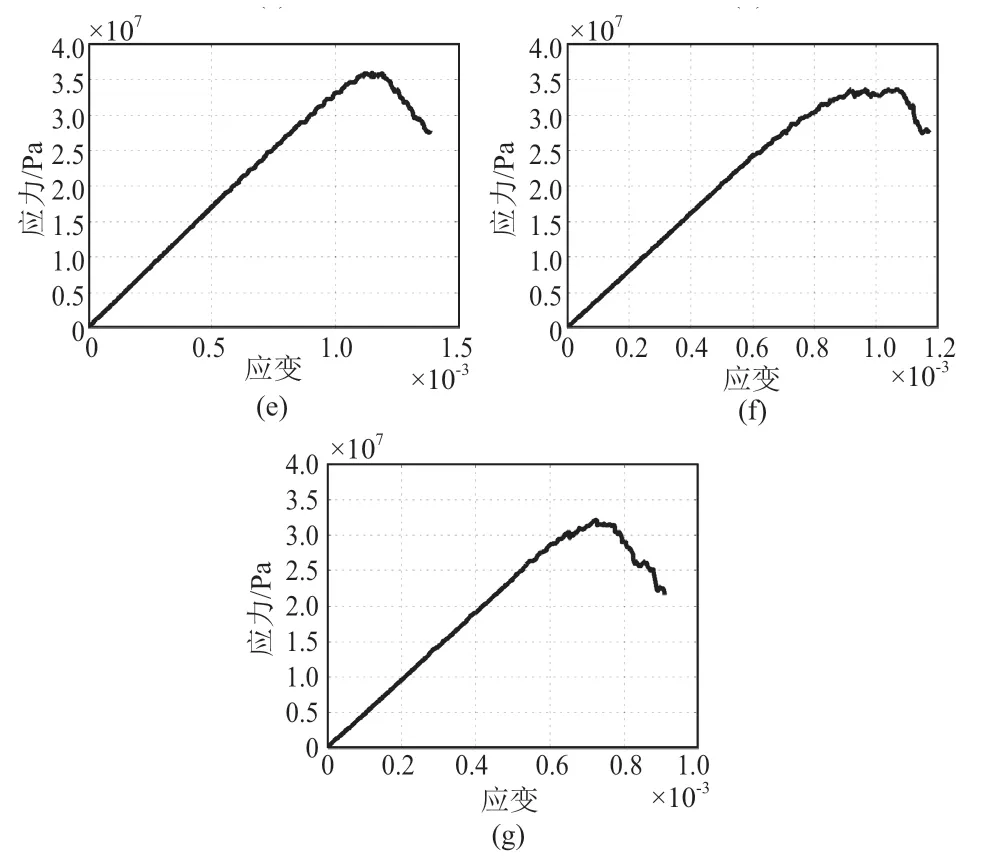
图2 颗粒接触模量单因子试验应力—应变曲线图

根据单因子试验，颗粒接触模量与模型弹性模量的关系见图3。

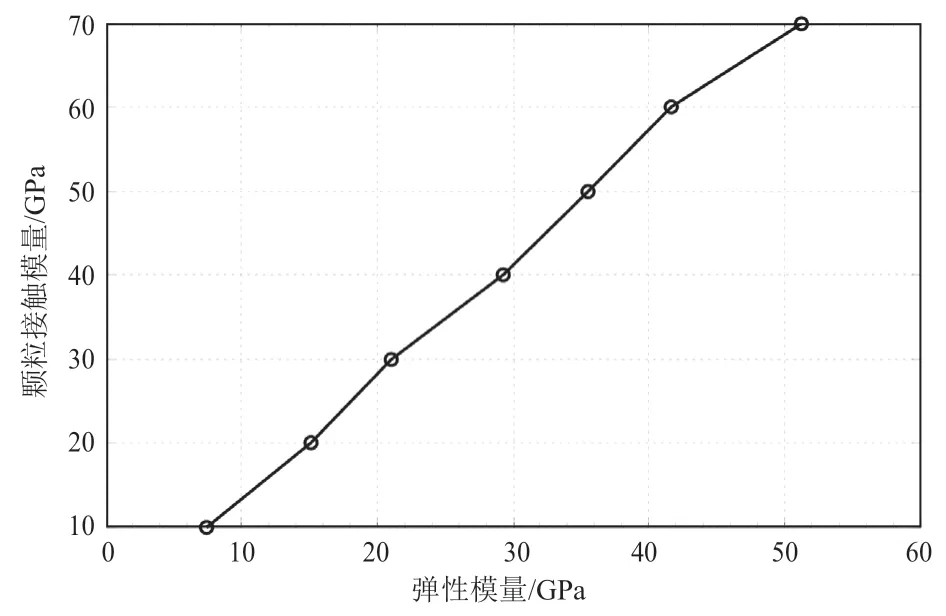
图3 颗粒接触模量对模型弹性模量的影响图

3.2.2 法向接触强度/切向接触强度

对法向接触强度/切向接触强度这一细观参数进行单因子试验，法向接触强度/切向接触强度分别取10，20，30，40，50，60 MPa，其余参数与初始模型参数相同。建立6 个模型分别进行数值模拟得到应力—应变曲线（见图4）。

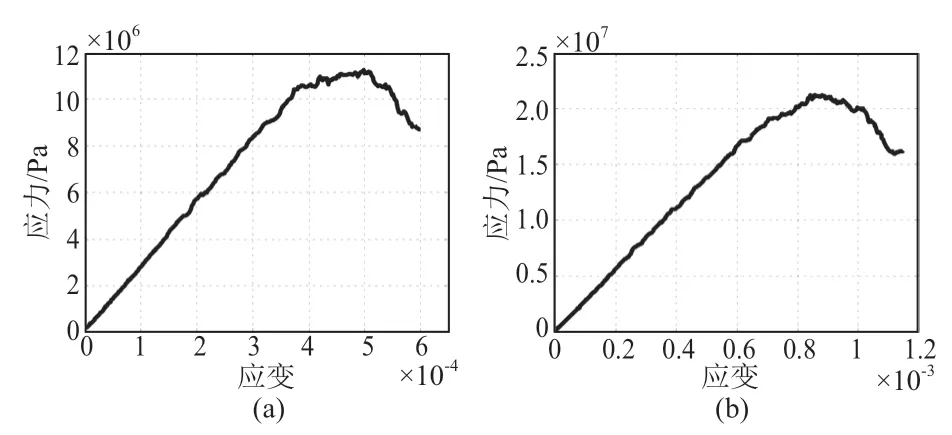
图4 法向接触强度/切向接触强度单因子试验应力—应变曲线图

根据单因子试验，法向接触强度/切向接触强度与模型单轴抗压强度的关系见图5。

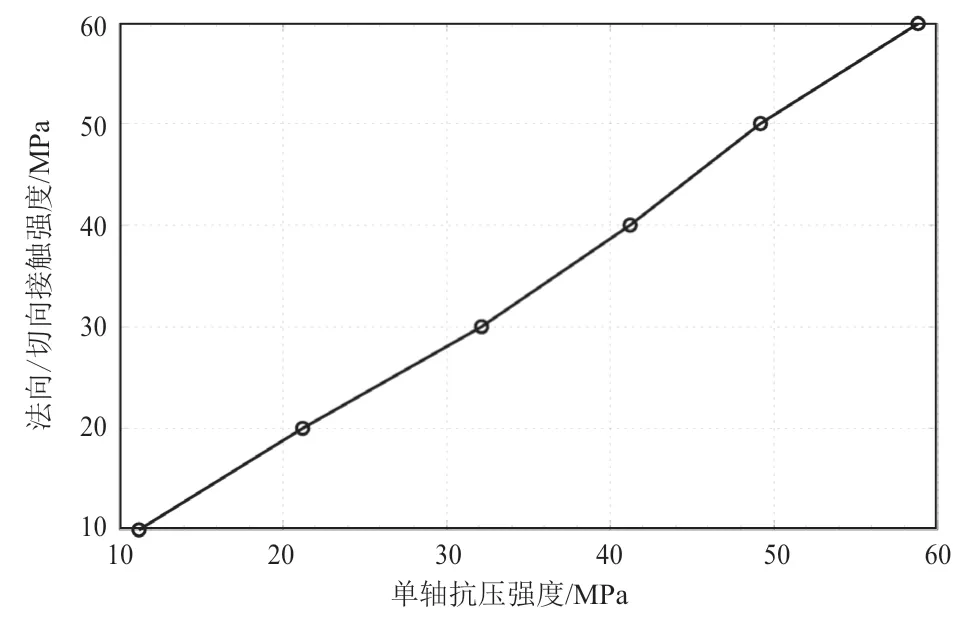
图5 法向/切向接触强度对模型单轴抗压强度的影响图

3.2.3 颗粒刚度比

对颗粒刚度比这一细观参数进行单因子试验，颗粒刚度比分别取0.5，1.0，1.5，2.0，2.5，3.0，3.5，其余参数与初始模型参数相同。建立7 个模型分别进行数值模拟得到应力—应变曲线（见图6）。

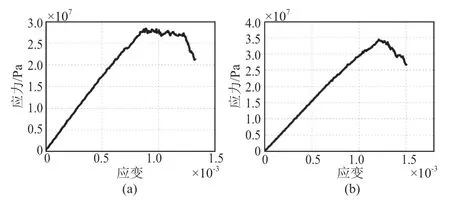
图6 颗粒刚度比单因子试验应力—应变曲线图

根据单因子试验，颗粒刚度比与模型泊松比的关系见图7。

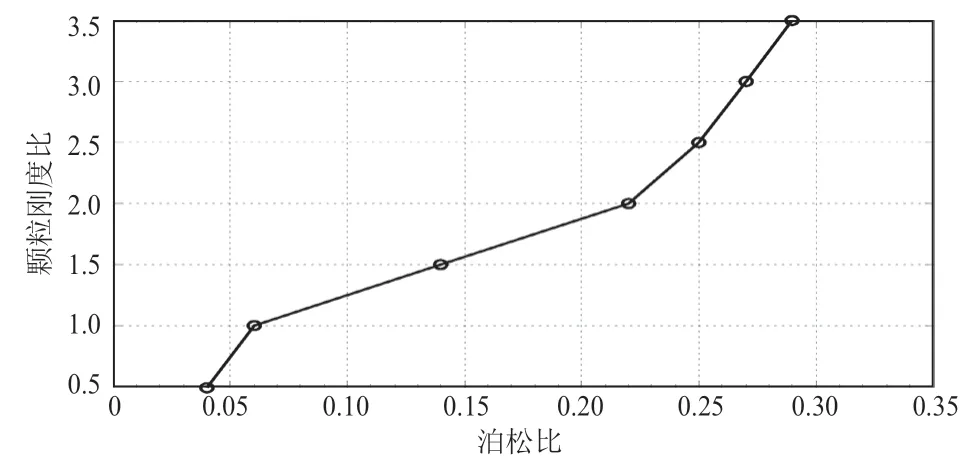
图7 颗粒刚度比对模型泊松比的影响图

3.2.4 因子水平确定

根据单因子试验结果，接触强度的-1 和+1水平分别设为20 MPa 和50 MPa，颗粒接触模量的-1 和+1 水平分别设为20 GPa 和60 GPa，颗粒刚度比的-1 和+1 水平分别设为1 和3，其余参数水平根据常规设置选取。最终，P-B 试验设计因子水平范围见表2。

表2 Plackett-Burman 试验设计因子水平表

3.3 Plackett-Burman 试验设计与结果分析

Minitab 是一种具有实验设计功能的统计软件，是一种研究与处理多因素试验的科学方法。Minitab 具有体积小、功能强大、操作简单、易于掌握、计算精确、兼容性好等特点，在影响因素众多且主因素不确定的情况下，通过筛选试验设计，经过少量试验即可找出主因素[11]。

本文采用Minitab 软件生成筛选试验设计表，根据P-B 试验设计进行12 次计算分析，设计及试验结果见表3。

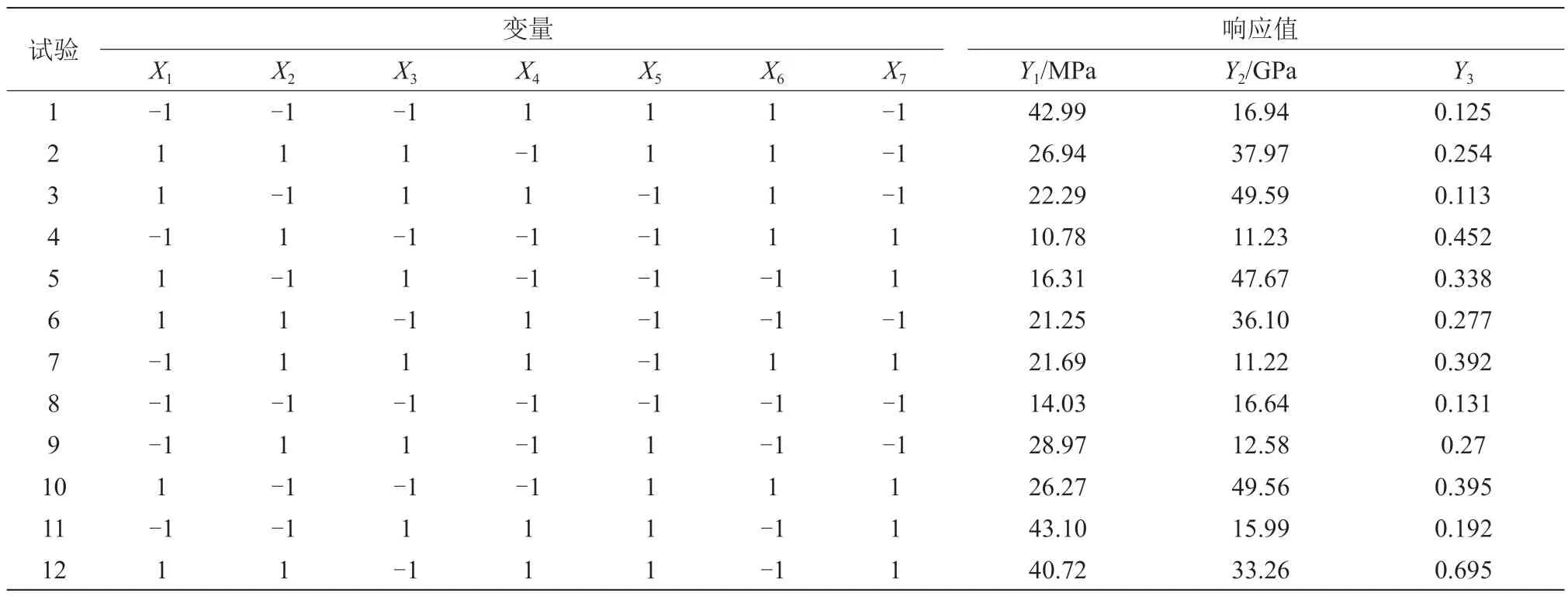
表3 Plackett-Burman 试验设计及响应值表

拟合一阶模型为：

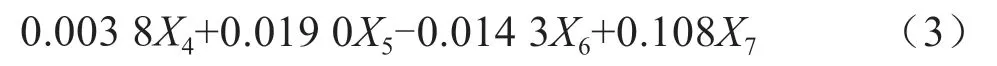
对模型进行方差分析（结果见表4）可知，所拟合的3 个回归方程均达到显著（P＜0.05），决定系数R2分别为0.985 0、0.991 0、0.916 0，表明分别用方程拟合7 个细观因子与3 个宏观力学特性之间的关系是可行的。

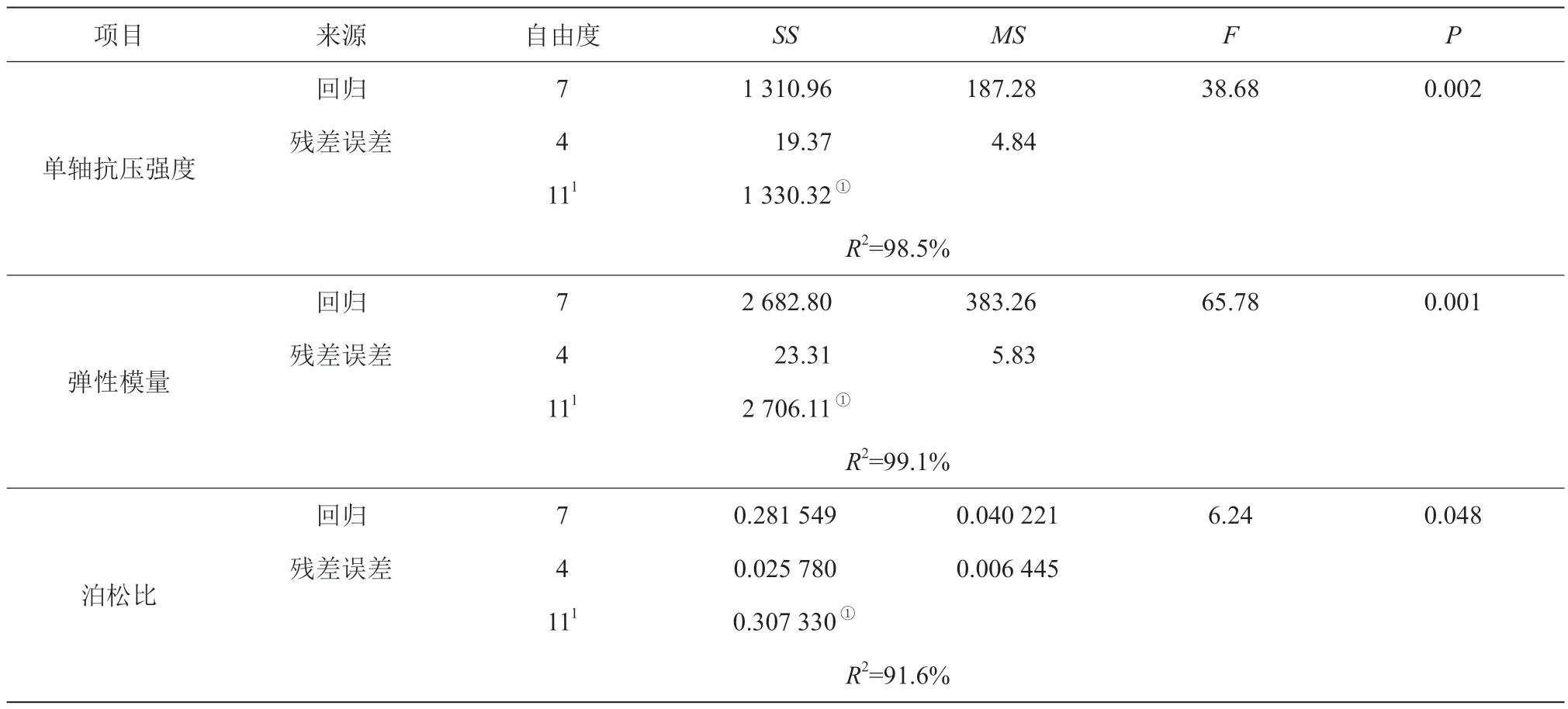
表4 回归模型方差分析表

实验回归方程系数显著性检验见表5。

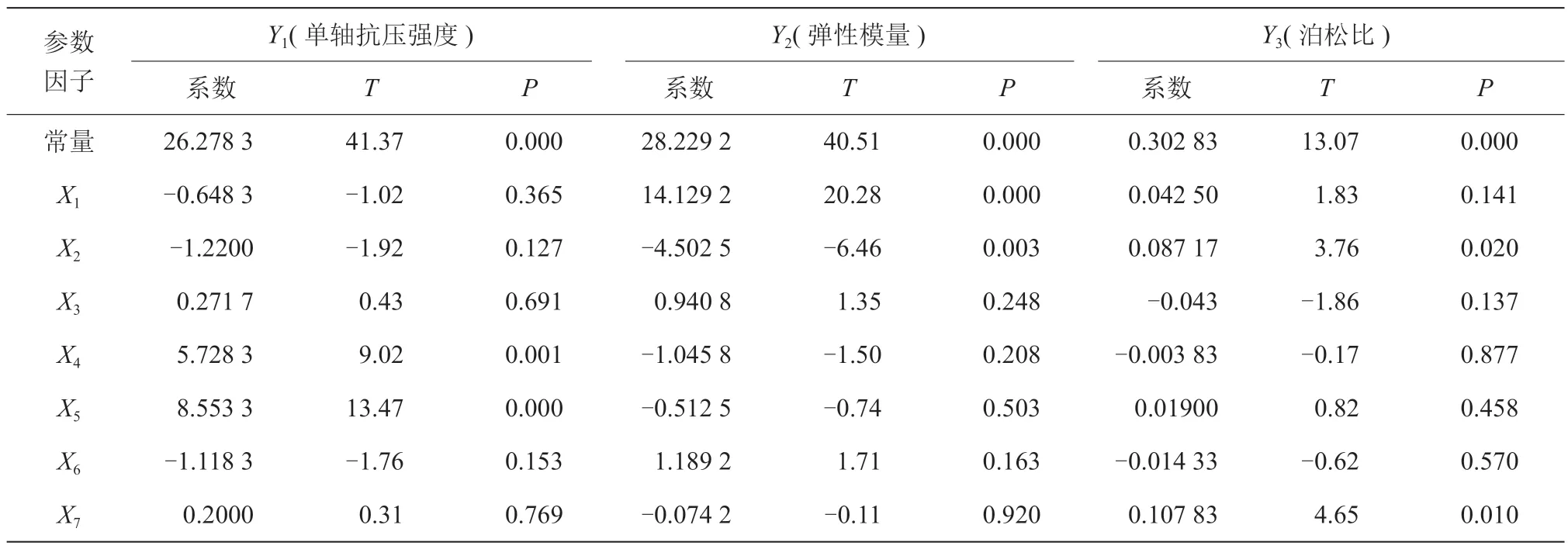
表5 回归系数的显著性检验表

由表5 可知，X4(法向接触强度)、X5(切向接触强度)对于单轴抗压强度具有显著性影响(P＜0.05)，即X4、X5为模型单轴抗压强度的主要影响因素，且影响因素的影响顺序为：X5＞X4。由T值可知，X4、X5对单轴抗压强度产生的影响均为正效应，因此增加X4、X5因子上的水平，会使单轴抗压强度增大。

X1(颗粒接触模量)、X2(颗粒刚度比)对于弹性模量具有显著性影响(P＜0.05)，即X1、X2为模型弹性模量的主要影响因素，且影响因素的影响顺序为：X1＞X2。由T值可知，X1对单轴抗压强度产生的影响为正效应，X2对弹性模量产生的影响为负效应，因此增加X1因子上的水平，减小X2因子上的水平，会使弹性模量增大。

X2(颗粒刚度比)、X7(最小颗粒半径)对于泊松比具有显著性影响(P＜0.05)，即X2、X7为模型泊松比的主要影响因素，且影响因素的影响顺序为：X7＞X2。由T值可知，X2、X7对泊松比产生的影响均为正效应，因此增加X2、X7因子上的水平，会使泊松比增大。

4 结语

通过P-B 试验设计研究模型宏观力学特性对于细观参数的敏感性响应，得出影响数值模型单轴抗压强度、弹性模量、泊松比的最主要细观参数，即：切向接触强度、法向接触强度这2 个细观参数是数值模型单轴抗压强度的主要影响因素，其中，切向接触强度是首要因素。颗粒接触模量、颗粒刚度比2 个细观参数是数值模型弹性模量的主要影响参数，其中，颗粒接触模量是首要因素。最小颗粒半径、颗粒刚度比2 个细观参数是数值模型泊松比的主要影响参数，其中，最小颗粒半径是首要因素。

文中阐述的影响各宏观力学特性的主要细观参数及影响顺序，能够便捷地调整试算方向及参数，有效降低细观参数选取的复杂性，为后续类似颗粒流数值计算提供参考。