复合墙体外表面材料性能对隔热效果的影响

樊智轩, 赵运超, 蒋达华, 符黄喜, 时雨

(江西理工大学土木与测绘工程学院， 赣州 341000)

《关于全面推进城镇老旧小区改造工作的指导意见》(国办发[2020]23号)指出：基础类改造的主要内容是“市政配套基础设施改造提升以及小区内建筑物屋面、外墙、楼梯等公共部位维修等。”中国2000年以前建造的城镇老旧小区内的住宅建筑，其外墙的保温隔热性能普遍较差，而中国建筑节能年度发展研究报告(2020版)指出：2018年，中国建筑能耗占全国能源消费总量的22%[1],其中暖通空调系统能耗占比最大。因此，在不改变建筑主体结构的前提下，如何借助墙体外表面材料的特性来提高建筑室内的热舒适性，降低空调系统的能耗，是一个非常值得关注的问题。

为提升墙体隔热性能，国内外众多学者对墙体隔热性能进行了大量的研究，取得了许多有意义的研究成果。孙孟琪等[2]研究了烧结保温砌块的孔洞形状、数量以及肋的数量对隔热效果的影响；Zhang等[3]研究发现,当墙体材料的导热系数小于1.0 W/(m·K)时,墙体具有良好的热工性能;当材料的导热系数和热容量分别大于1.0 W/(m·K)和 1.0 MJ/(m3·K)时,增大材料热容量比减小导热系数能更好地提高墙体的热工性能；程飞等[4]利用能耗模拟软件计算不同工况下,建筑空调能耗随外墙传热系数的变化特性，结果表明,存在一个外墙传热系数值使建筑全年空调能耗最小；针对冬季工况，张洋等[5]基于平均传热系数法分析了墙体厚度变化对高层建筑墙体内表面温度的影响，确定了建筑墙体各部位不同保暖材料的最优经济厚度；文献[6-8]建立了复合外墙非稳态传热模型,研究了能耗随保温层厚度的变化特性；高飞[9]研究了不同吸收系数的建筑饰面材料对建筑能耗的影响，结果表明建筑饰面材料选用吸收系数较小的能减小夏季空调能耗。王亮等[10]合成了一种新型保温材料-气凝胶膨胀珍珠岩,可制得导热系数低至 0.062 W/(m·K)的保温隔墙板；Simona等[11]介绍了用于分析建筑均质墙和复合墙一维稳态传热分析方法,开发了分析墙体内部温度场的网页应用程序；严清等[12]提出了一种排风隔热墙并研究了在周期外扰下排风隔热墙的非稳态传热特性。赵运超等[13]研究发现，当选用蓄热系数小、热惰性指标大的外表面材料时，温度波动较大且衰减较速度快，墙体内表面最高温度较低。文献[14-15]一致认为，使用保温隔热材料都能有效降低暖通空调系统能耗，提高室内人员热舒适性。但关于外表面材料如何合理选取,以及外表面材料热物理性能如何影响复合墙体隔热性能方面的研究较少。

因此，现以夏热冬冷地区(以赣州市为例)复合墙体的外表面材料为研究对象，以复合墙体内表面温度为目标参数，建立复合墙体在夏季周期性室外气象参数条件下的动态传热模型并进行数值求解，研究复合墙体外表面材料性能对其隔热特性的影响，探索提升建筑墙体隔热性能、降低墙体内表面温度的措施，为老旧小区建筑墙体改造以及新建建筑墙体外表面的选材、制备等提供理论指导。

1 复合墙体瞬态传热模型及求解

1.1 复合墙体瞬态传热模型

假设某建筑外墙的结构为三层材料组成的复合墙体将其置于室外环境中，热量由复合墙体外表面向内表面传递。其结构如图1所示。

1为外层；2为中间层；3为内层图1 墙体结构图Fig.1 Wall structure diagram

1.2 动态传热微分控制方程

为简化计算，做如下假设：①忽略墙体在垂直热流方向的传热，即一维大平板瞬态传热；②建筑外墙各层材料的物性参数均匀且各向同性；③各层材料接触良好，无空气间层；④无内热源。

则复合外墙一维瞬态无内热源导热的微分控制方程为

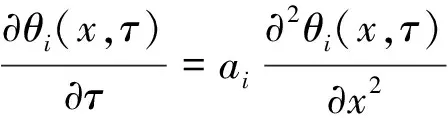
(1)

(2)

θ0(x,τ)=t0(x,τ)-tw,m,τ=0

(3)

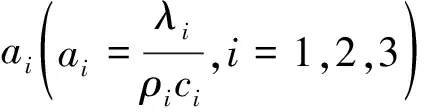
1.3 导热微分方程的求解

采用有限元法对该一维无内热源瞬态导热微分方程进行求解。

该问题的泛函为

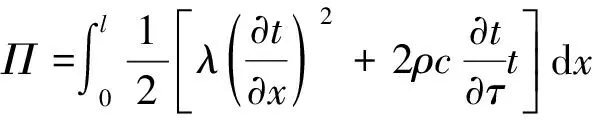
(4)

求解泛函可得

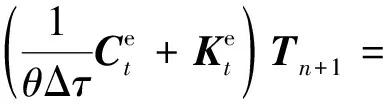
(5)

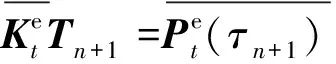
(6)

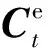
借助ANSYS软件进行数值求解，获得复合墙体内表面温度的动态响应。设定初始时刻墙体内部温度均匀一致，墙体外表面选择第一类边界条件，按照网格精度[16]0.005网格划分后，共3 535个节点，3 600个单元，如图2所示；时间步长取60s，求解总时间为86 400s。

图2 网格划分 Fig.2 Meshing

2 数学模型可靠性验证

为并验证该文所建数学模型及其数值计算结果的可靠性，搭建了复合墙体性能测试实验平台。在室外非稳态气候条件下，实测复合墙体内表面温度。

2.1 实验装置及测试方案

搭建的复合墙体性能测试小室如图3所示，其尺寸为500 mm×500 mm×500 mm，四周空旷无遮挡。墙体结构各层材料的热物性参数如表1所示。

测试时间为2020年7月11号，测试地点为赣州市某大学校园内。本实验采用热电偶测试复合墙体内外表面温度，数据采集装置为安捷伦34972A型，60 s测量保存一次数据；在复合墙体内表面的每个面分别布置两个测点，其中纵深方向在同一直线上，上下、左右两点之间的距离分别为150、120 mm，呈1×2形式分布；在复合墙体的外表面布置1个温度测点，布置在复合墙体外表面中心点，测点布置如图4所示。

表1 墙体物性参数表

2.2 测试结果及可靠性验证

为了验证传热模型的可靠性，笔者将数值计算结果与实测数据进行对比，结果如图5所示。

图3 测试小室Fig.3 Test chamber

图4 测点布置图Fig.4 Layout of points

图5 复合墙体内表面计算温度与实测温度的对比Fig.5 Comparison of the calculated and measured temperature on the inner surface of composite wall

由图5可知，复合墙体内表面的温度的计算值与其实测值在变化趋势上基本一致，都是随着室外温度的周期性变化呈现出周期性的变化规律，数值计算出的复合墙体内表面温度在9：50达到温度最小值23.36 ℃，18：55达到温度最高值38.07 ℃；实验得到的墙体内表面温度在9:02达到最小值22.53 ℃，在17：55达到温度最大值40.20 ℃，计算得到峰值温度的偏差为5.3%,计算峰值温度出现时刻较实测峰值温度出现时刻延迟了1 h，谷值温度的偏差为3.7%；计算谷值温度出现时刻较实测出现时刻延迟了48 min，这主要是由于复合墙体理论计算是在一定的假设条件下进行了简化，而实际传热过程较为复杂。总体而言，该理论模型及数值计算结果与实测值吻合良好，从而验证理论模型及数学计算方法的可靠性。

3 影响因素分析

下面重点分析复合墙体外表面材料的热物性参数(密度ρ、导热系数λ、比热c)对其内表面温度的影响。

3.1 外表面材料密度对复合墙体内表面温度的影响

以西向墙体为例，当复合墙体主体材料选用表1中的120 mm普通砖，内表面选用水泥砂浆时，保持其他条件参数均不变，复合墙体外表面材料的密度范围取：40～2 040 kg/m3，步长取500 kg/m3。经数值计算得到墙体内表面峰值温度随外表面材料密度的变化曲线如图6所示(标注为峰值出现时刻)。

图6 密度与墙体内表面峰值温度的关系Fig.6 The relationship between the density of outer surface and the peak temperature of inner surface

从图6可以看出，在随着墙体最外表面材料密度的增加，墙体内表面峰值温度随之降低。但随着墙体外表面材料密度的增加，墙体内表面峰值温度减小量和峰值出现时刻延迟都非常小，当密度ρ=40 kg/m3时，对应墙体内表面温度峰值为 38.11 ℃，出现时刻为18：50；当密度ρ=2 040 kg/m3时，对应墙体内表面温度峰值为38.06 ℃出现时刻为18：56，降幅仅为0.05 ℃。因此，在符合建筑结构力学要求范围内，靠外表面选择材料密度大的材料，对复合墙体隔热性能的影响很小。

3.2 外表面材料导热系数对复合墙体内表面温度的影响

以西向墙体为例，当墙体主体材料选用表1中的120 mm普通砖，内表面选用水泥砂浆时，保持其他条件及参数均不变，墙体外表面材料的导热系数范围取0.03～2.43 W/(m·K)，步长取0.3 W/(m·K)，经数值计算，得到墙体内表面逐时温度曲线，如图7所示。并对导热系数和其对应的内表面峰值温度值及出现时刻进行曲线拟合。

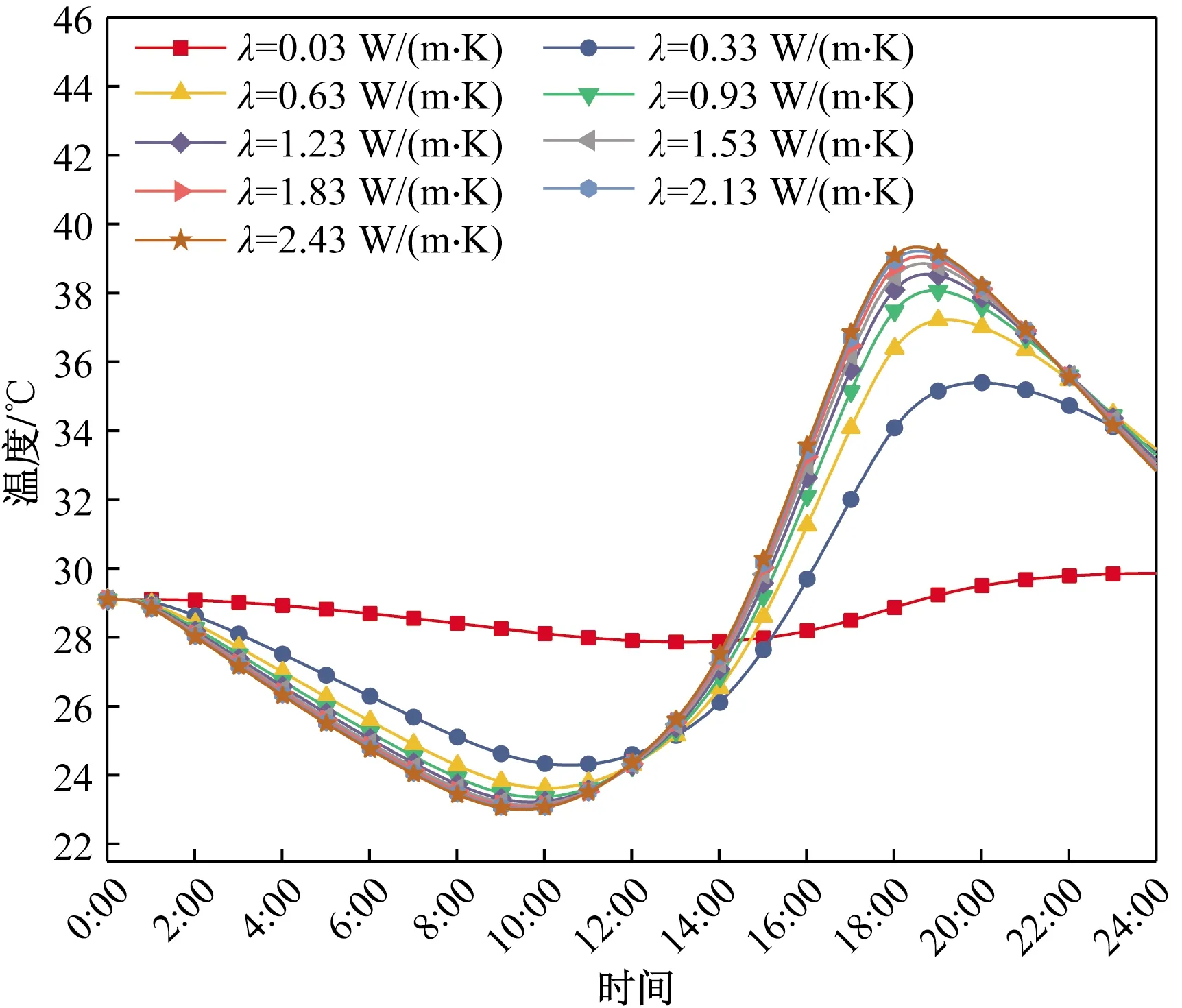
图7 墙体外表面材料导热系数对内表面温度的影响Fig.7 The effect of thermal conductivity of the outer layer material of the composite wall on the inner surface temperature

经过拟合得到导热系数和其对应的内表面峰值温度值的关系式为

tm(λ)=37.86e0.016 46λ-8.91e-3.57λ

(7)

式(7)中：tm(λ)为内表面峰值温度；λ为复合墙体外表面材料导热系数，该关系式的相关系数R2=0.999 6，拟合精度高，具有可信度。拟合曲线如图8所示。

得到导热系数和其对应的内表面峰值温度出现时刻的关系式为：

τtm(λ)=344.8e-5.483λ+1 148e-0.014 48λ

(8)

式(8)中:τtm(λ)为内表面峰值温度出现时刻；λ为复合墙体外表面材料导热系数，该关系式的相关系数R2=0.999 5，拟合精度高，具有可行度。拟合曲线，如图8所示。

从图7可以看出，在0:00—12:00时段内，复合墙体内表面温度随着外表面材料导热系数的增大变化量非常小，这主要是由于在此时段内西向墙体接收太阳辐射较少导致的；在12:00—24:00时段内，复合墙体内表面温度随着外表面材料导热系数的减小而降低，峰值最大降幅为9.47 ℃，内表面峰值温度出现时刻随着外表面材料导热系数的减小而延迟，最大延迟了5 h 29 min。同时结合图8和式(6)、式(7)发现，峰值温度的升高速率随材料导热系数增大而减小，峰值温度出现时刻的提前速率随材料导热系数的增大而减小。原因分析：由于材料的导热系数是在稳态传热条件下通过一定的试验测试得到的表征材料传热性能的一个参数，但在墙体瞬态传热过程中，由于墙体内外表面的温度差是变化的，导热系数越大，对墙体内表面温度波幅的影响越小，相反，导热系数越小，对墙体内表面温度波幅影响越大。因此，确定墙体外表面材料时，在满足要求的情况下尽量选择导热系数小材料。

图8 导热系数与内表面峰值温度及其出现时刻的关系Fig.8 The relationship between thermal conductivity and the peak temperature of inner surface and time of occurrence

3.3 外表面材料比热对复合墙体内表面温度的影响

当墙体主体材料选用表1中的120 mm红砖，内表面选用水泥砂浆时，保持其他条件参数均不变，墙体外表面材料的比热范围取0.5～240.5 kJ/(kg· K)，步长取30 kJ/(kg· K)。经数值计算，得到墙体外表面材料取不同比热时内表面温度逐时变化曲线，如图9所示。

对材料比热和其对应的内表面峰值温度值及出现时刻曲线拟合，得到导热系数和其对应的内表面峰值温度值的关系式为

tm(c)=8.052e-0.013 13c+30.12e-3.628×10-5

(9)

式(9)中：tm(c)为内表面峰值温度；c为复合墙体外表面材料比热。该关系式的相关系数R2=0.999 97，拟合精度高，具有可行度。拟合曲线如图10所示。

得到导热系数和其对应的内表面峰值温度出现时刻的关系式为

τtm(c)=-393.6e-0.015 34c+1 524e0.000 769 9c

(10)

式(10)中：τtm(λ)为内表面峰值温度出现时刻；c为复合墙体外表面材料比热。该关系式的相关系数R2=0.999 99，拟合精度高，具有可信度。拟合曲线如图10所示。

从图9可以看出，随着复合墙体外表面材料比热的增大其内表面峰值温度降低，延迟时间更长。结合图10和式(8)、式(9)不难发现，比热由 0.5 kJ/(kg·K)变为240.5 kJ/(kg·K)，峰值温度降

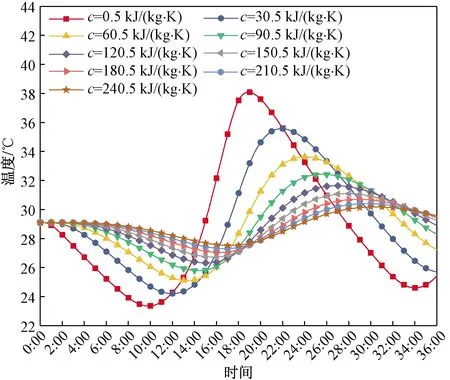
图9 墙体外表面材料比热对内表面温度的影响Fig.9 The influence of the specific heat of outer layer material of the wall on the temperature of the inner surface

图10 比热与内表面峰值温度及其出现时刻的关系Fig.10 The relationship between the specific heat and the peak temperature and the appearance time

低了7.9 ℃，峰值温度出现时刻也延迟了11 h 30 min。峰值温度的降低速率随材料比热增大而减小，峰值温度出现时刻的延后速率随材料比热的增大而减小。因此，在其他条件不变的情况下，改变墙体外表面材料的比热，能够降低内表面温度，延迟峰值温度出现时刻。但传统建筑隔热材料比热很难达到3 kJ/(kg·K)以上，想要通过增加比热提高墙体隔热性能，可以选择比热或者等效热容大的材料，如相变材料，同时需要根据比热和其对应的内表面峰值温度及其出现时刻的关系式，结合经济因素，确定合理的材料比热或等效比热。

4 结论

以墙体内表面温度为目标参数，通过研究复合墙体外表面材料性能对其隔热性能的影响，发现墙体外表面材料的各个参数对内表面温度的影响程度和效果是不同的，分析结论如下：

(1)在符合建筑力学要求条件下，改变复合墙体外表面材料的密度对其内表面瞬时温度的和延迟时间的影响均很小。

(2)在其他条件参数不变的条件下，得到了复合墙体外表面材料的导热系数和其对应的内表面峰值温度值及出现时刻的关系式，发现了以下变化规律。随着外表面材料导热系数的增大，复合墙体内表面的峰值温度的升高速率随之减小，而且峰值温度出现时刻提前速率减小。

(3)在其他条件参数不变的条件下，得到了复合墙体外表面材料的比热和其对应的内表面峰值温度值及出现时刻的关系式，发现了以下变化规律：随着复合墙体外表面材料比热的增大其内表面峰值温度降低速率减小，峰值温度出现时刻延后速率减小。

(4)为了获得良好的隔热效果，必须选择导热系数小、比热大的隔热材料，而传统建筑材料比热通常不超过3 kJ/(kg·K)，对墙体隔热的影响小。而相变材料通常具有较小的导热系数、相变过程中具有非常大的等效热容，并且具有较大的潜热储存和释放能力，为提高建筑外墙隔热效果提供了研究思路。