基于方箱的气浮工作台控制系统稳定性分析＊

朱思达 卢志伟 刘 波 张君安

（西安工业大学机电工程学院，陕西 西安 710021）

随着现代科技的飞速进步，精密与超精密加工技术在各国科技产品竞争和军事装备竞争中扮演着越来越重要的角色。精密与超精密加工技术既是国家现代高新技术的重要发展方向，也对现代基础科学技术的发展提供了保障。如今各国对精密及超精密加工设备的需求量在不断增加，而这其中精密和超精密运动导轨和运动工作台为超精密加工、光学精密测量及半导体等领域提供了重要的技术支撑，是众多高技术产业的基础保障。精密二维工作台是实现精密加工和精密加工的重要功能载体，它的性能直接影响了零部件的加工精度和效率。现如今能实现精密运动的高性能二维气浮工作台应用领域越来越广泛，因而对气浮工作台的性能提出了更高的要求[1]。

气浮工作台是由复杂的机械运动学以及伺服控制学所集成的系统。对于气浮工作台而言，最终要实现的目标为：能够按照给定轨迹精密运动以及精准定位。其实现精密运动，不仅仅需要依靠精密运动导轨以及高精度电机，还需要拥有稳定且精准的伺服控制系统[2]。由于气浮工作台采用气浮导轨支承技术，使得整个工作台阻尼小、惯性力大，易造成控制系统的不稳定，最终可能导致机械设备寿命减少、性能降低，甚至设备损坏的后果。因此需要对伺服控制系统的稳定性进行分析研究，以避免造成严重后果。

安徽大学王立军采用离散的李雅普诺夫函数去选择满足系统稳定的自适应增益，充分抑制系统扰动，提高系统的鲁棒性[3]。西安理工大学尹忠刚构建基于永磁同步直线电机数学模型的无差拍电流预测控制算法，得到了算法的稳定域，使控制算法在电机参数摄动范围内稳定[4]。哈尔滨工业大学陈伟通过控制无功电流恒定调节输出电压来抑制电机振荡，提高系统的稳定性[5]。西安电子科技大学苏玉鑫采用波波夫判据对闭环控制系统进行稳定性分析，确保非线性闭环控制系统稳定的非线性增益的有效取值范围[6]。

本文以二维气浮工作台伺服控制系统为例，采用伯德图稳定性分析法，建立各环控制器开环传递函数，利用Matlab 计算出伯德图，根据工程指标进行稳定裕度分析，对于出现不稳定状态进行了参数修正，并建立实验单元验证了控制系统的稳定性。为各类气浮工作台伺服控制系统的参数设计和稳定性分析打下了基础。

1 二维气浮工作台及驱动控制系统

课题组研制的一种基于精密计量方箱的精密二维气浮静压平面运动平台主要由机械结构系统、气动系统和驱动控制系统组成。机械结构部分主要由精密计量方箱、X轴气浮导轨、Y轴气浮导轨、直线电机、光栅尺位移传感器以及伺服驱动器、控制卡所构成。二维气浮工作台如图1 所示[7]。

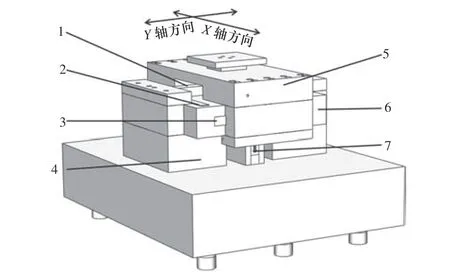
图1 二维气浮工作台

二维气浮工作台各轴向的控制系统均采用全闭环控制，全闭环控制系统是由电流环、速度环、位置环构成，其中电流环为最内环，采用PI 调节方式；速度环为中环，同样采用PI 调节方式；位置环为最外环，采用P 调节方式。驱动控制系统结构如图2 所示。

图2 驱动控制系统结构图

2 驱动控制系统数学模型

2.1 直线电机数学模型

直线电机的运行原理与旋转电机的运行原理相类似。在理想条件下，建立直线电机在d-q模型下电流模型方程如下。

式中：Ud、Uq分别是直线电机动子电压d、q轴分量，V；id、iq分别是直线电机动子电流d、q轴分量，A；Ld、Lq分别是直线电机动子电感d、q轴分量，H；R为电枢绕组的电阻，Ω；ω为直线电机等效转子角速度，rad/s，且 ω=(π/τ)PnV，V为动子运动速度，m/s；τ为磁极距，mm；Pn为动子线圈的极对数，φf为永磁体磁势，Wb。

在假设没有任何干扰的情况下，计算直线电机的电磁推力如下。

输出总功率为

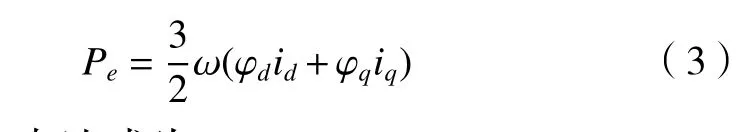
电磁推力表达式为

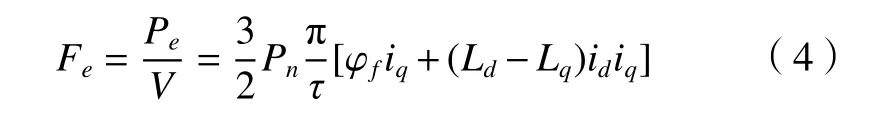
对于U 型平板式直线电机，Ld、Lq相等，所以简化电磁推力方程为

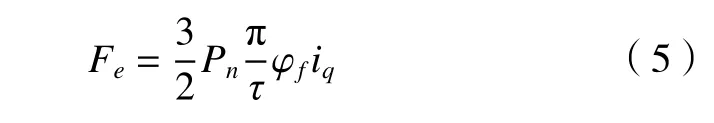
根据牛顿第二定律，直线电机机械运动方程为

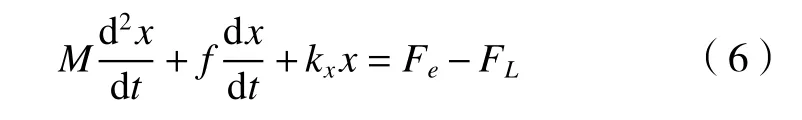
式中：M为运动部件质量，kg；x为动子位移量，m；f为工作台与导轨之间的摩擦系数；kx为弹性系数；Fe为 电机电磁推力，N；FL为负载干扰力，N。

对于二维气浮工作台，可以将摩擦力忽略。在id=0以及电压确定的条件下，可以推导出直线电机状态平衡方程为[8]

在初始值为零时，将式（7）进行拉氏变换，并以电压作为信号输入，动子运动速度作为信号输出。

气浮工作台直线电机相关参数如表1 所示。

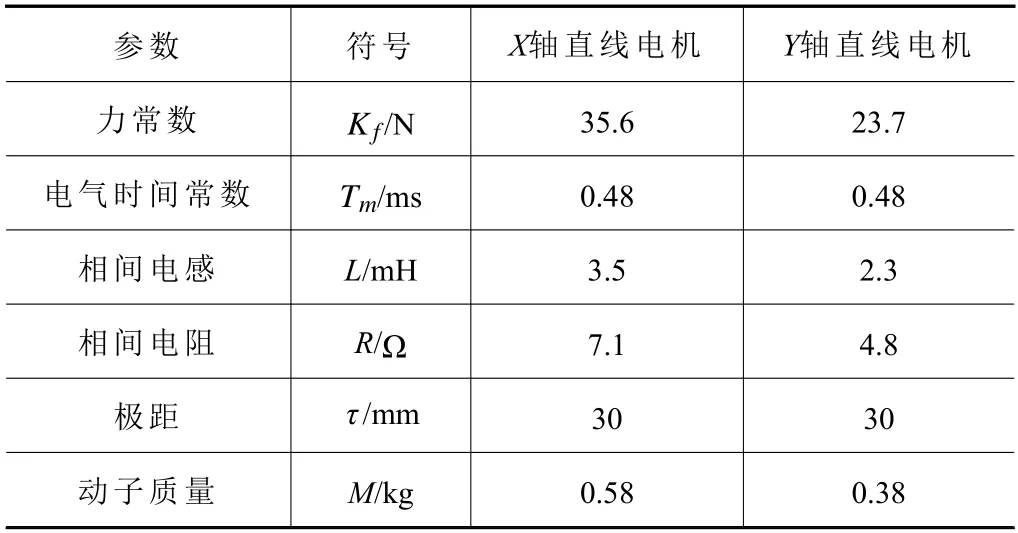
表1 直线电机参数表

2.2 电流环PI 控制器数学模型

在本系统中，电流环作为控制系统最内环，建立电流环PI 控制器闭环函数GiB(S)以及相应的开环函数Gi(S)。

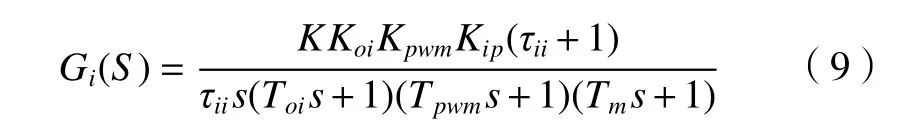
式中：Koi为电流反馈滤波放大系数，V/A；Kpwm为逆变器放大倍数；τii为 时间积分常数，s；Toi为滤波时间常数，s；Tpwm为 逆变器时间常数，s；Tm为电气时间常数，s；Kii为电流积分调节系数，V/A。

由式（9）得，Y轴电流环开环传递函数：

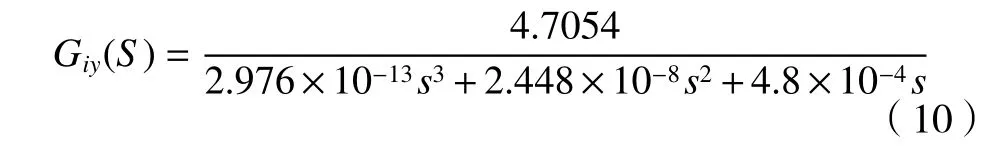
同样可以得到X轴电流环开环传递函数：

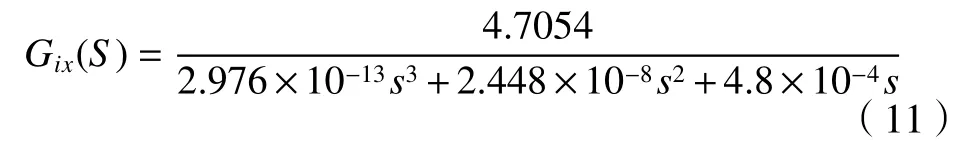
2.3 速度环PI 控制器数学模型

根据控制系统的设计原则，速度环以电流环为内环，采用PI 控制器调节[9]，PI 控制器传递函数为

式中：Kvp为 速度环控制器比例系数，As/mm；Tvi为速度环积分时间系数，s。

建立速度环 PI 控制开环传递函数

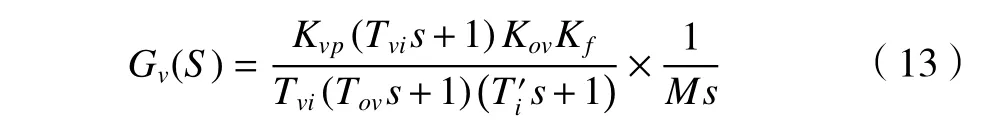
式中：Kvi=Kvp/Tvi；Kov为速度环反馈放大系数；Tov为速度环滤波时间常数，s；M为平台质量，kg；Kf为推力常数。

将2 个时间常数Tov和Ti’的合并，则式（13）简化为

在Y轴中，M=59.4 kg，Kf=23.7 N/A。故，Kvp=23.467 As/mm，Kvi=4 084.73。Y轴速度环开环C传递函数为

在X轴中，M=121 kg，Kf=35.6 N/A。故，Kvp=31.82 As/mm，Kvi=5 680.78。X轴速度环开环传递函数为

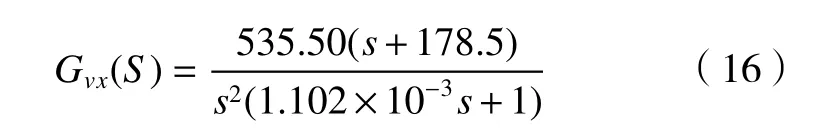
2.4 位置环P 控制器数学模型

位置环是以速度环为内环的，本系统位置环采用P 控制。建立位置环开环传递函数

式中：KPP为位置环比例系数；GvB(S)为速度环闭环传递函数。

式中：Gv(S)为速度环开环函数。

由式（15）与（16）可推导出Y、X轴速度环闭环函数

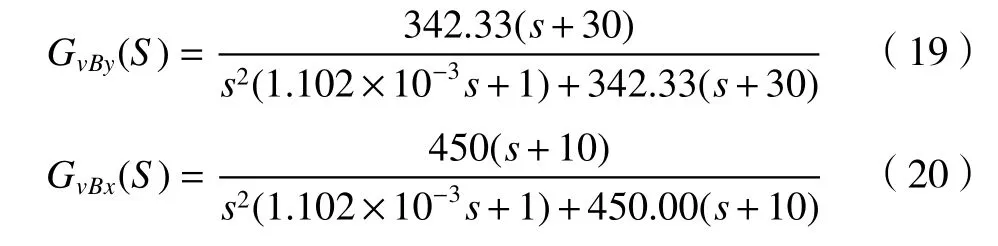
在位置伺服系统中，为了提高系统的抗干扰性应尽量使比例增益取大值。可以将位置环比例增益作适当修正。取KPPx=40，KPPy=200。由式（17）可推导出Y、X轴位置环开函数

3 驱动控制系统稳定性分析

3.1 电流环稳定性分析

Matlab 的工具箱中提供了Bode()命令，使得求解过程变得简便。由式（10）与（11）可知Y轴与X轴电流环的开环传递函数。根据所推导的传递函数绘制伯德图，控制系统电流环伯德图如图3 所示。

对控制系统电流环开环传递函数进行稳定裕度分析，从图3 中可以得知：X轴与Y轴轴相角裕度均为63.5°＞60°，幅值裕度均为18.5 dB＞10 dB，满足系统稳定裕要求，系统电流环是稳定的。

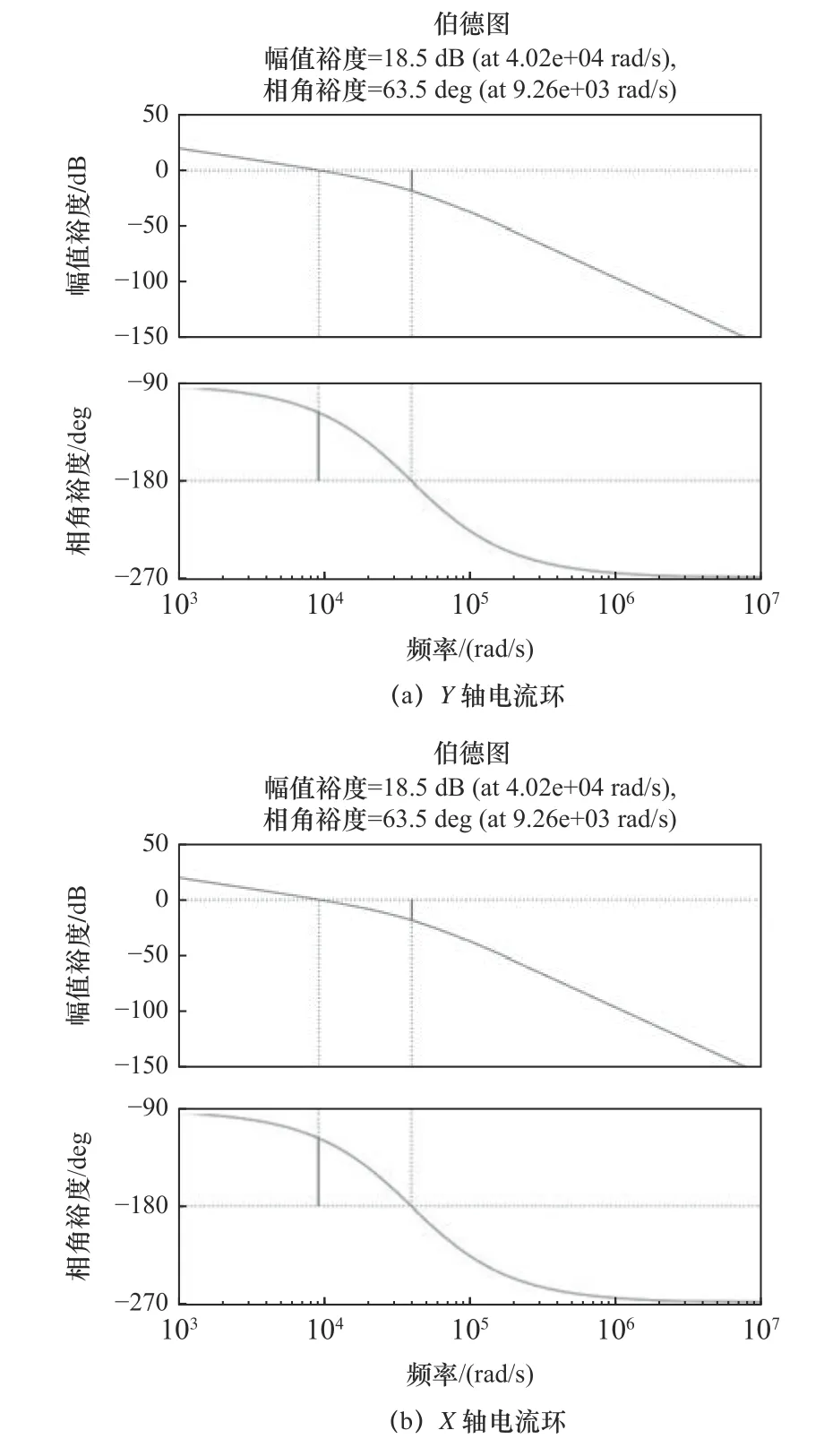
图3 电流环伯德图

3.2 速度环稳定性分析

由式（15）与（16）可知，Y轴与X轴速度环的开环传递函数。根据所推导的传递函数绘制伯德图，控制系统速度环伯德图如图4 所示。

对控制系统速度环开环传递函数进行稳定裕度分析，从图4 可以得到：X轴与Y轴速度环相角裕度都小于60°，不能满足稳定裕度要求。

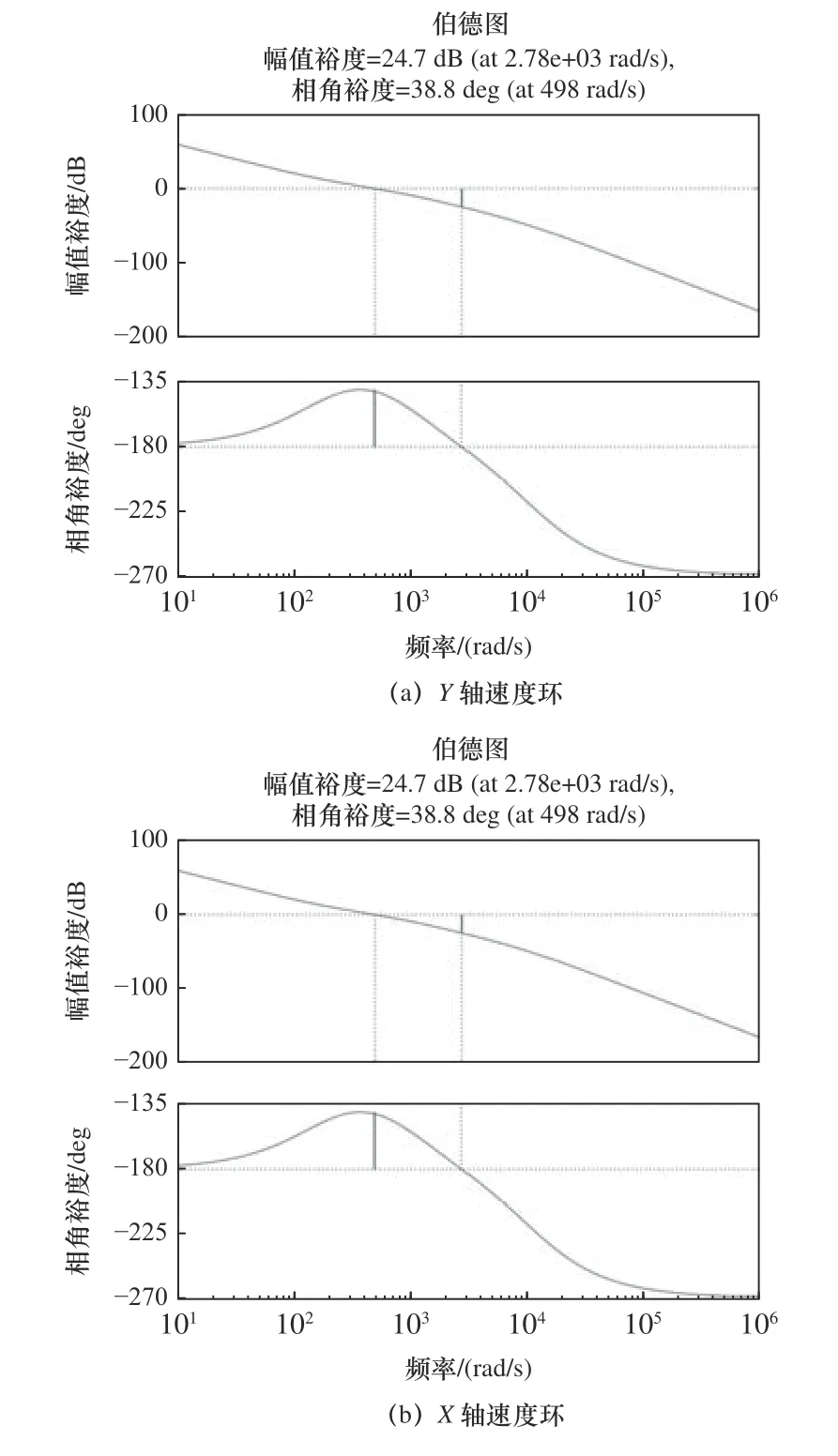
图4 速度环伯德图

修正后Y轴：Kvp=15，Kvi=2 713.45。

修正后X轴：Kvp=26.74，Kvi=4 853。

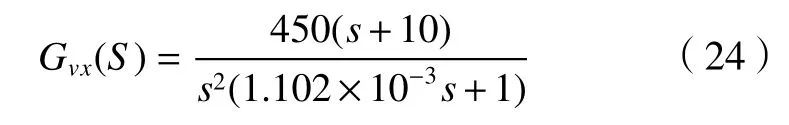
修正前分析造成不满足稳定裕度的原因：工作台用气浮导轨支撑使得工作台阻尼很小，直线电机直接驱动无缓冲，这些因素都可能造成系统稳定裕度不能这到要求。

对修正后速度环开环传递函数进行稳定裕度分析，由图5 可以得到：修正后Y轴速度环开环传递函数相角裕度为63.3°＞60°，幅值裕度为30.4 dB＞10 dB；X轴速度环开环传递函数相角裕度为62°＞60°，幅值裕度为28.2 dB＞10 dB，满足系统稳定裕度要求，系统速度环为稳定的[10]。

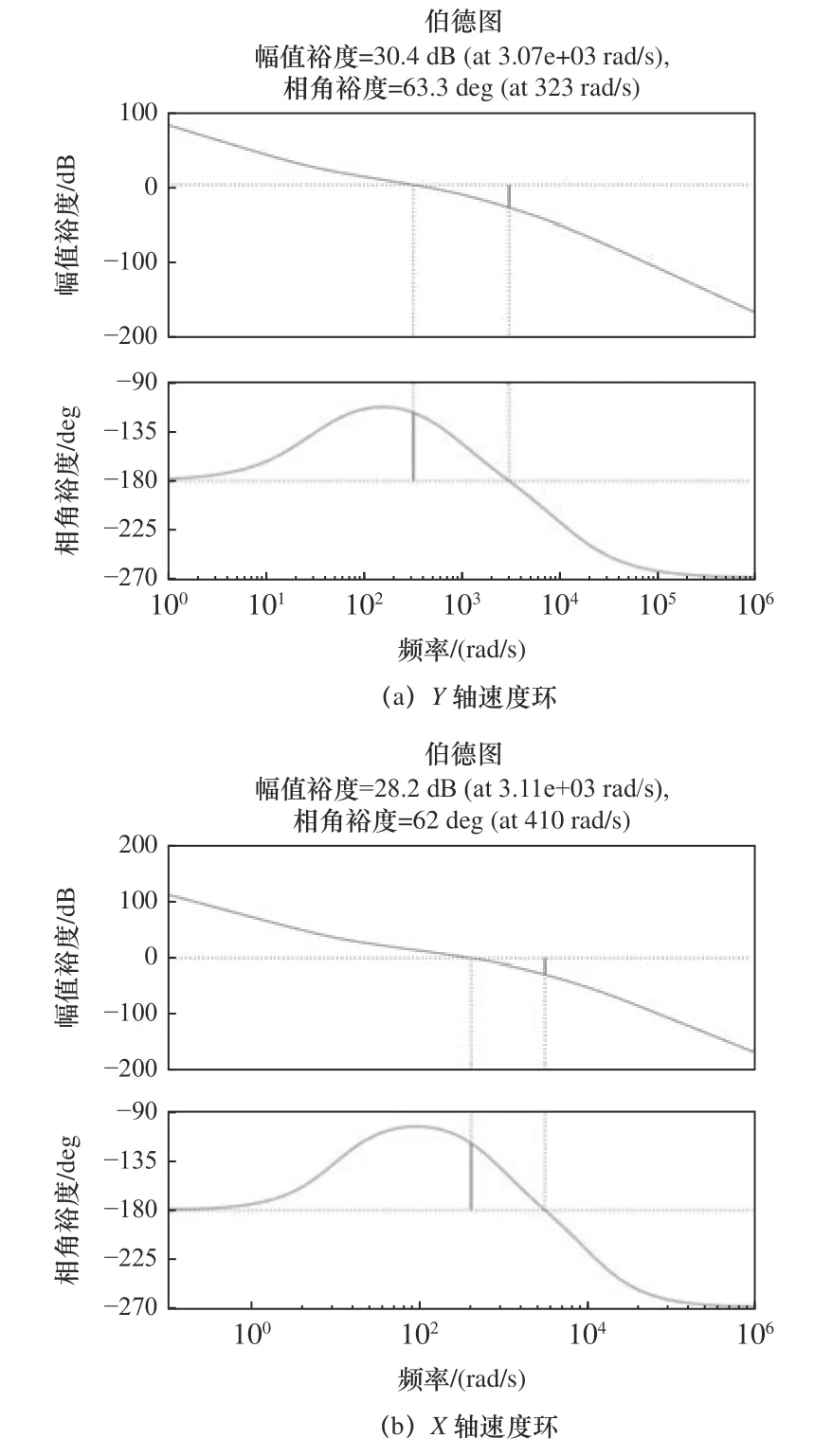
图5 修正后速度环伯德图

3.3 位置环稳定性分析

由式（21）与（22）可知，Y轴与X轴位置环的开环传递函数。根据所推导的传递函数绘制伯德图，控制系统速度环伯德图如图6 所示。

对控制系统位置环开环传递函数进行稳定裕度分析，从图6 可以得到：Y轴直线电机位置环开环传递函数相角裕度为85.1°＞60°，幅值裕度为26 dB＞10 dB；X轴直线电机位置环开环传速函数伯德图如b 图所示，其相角裕度为63.1°＞60°，幅值裕度为12.8 dB＞10 dB。满足系统稳定裕度要求，系统位置环为稳定的。

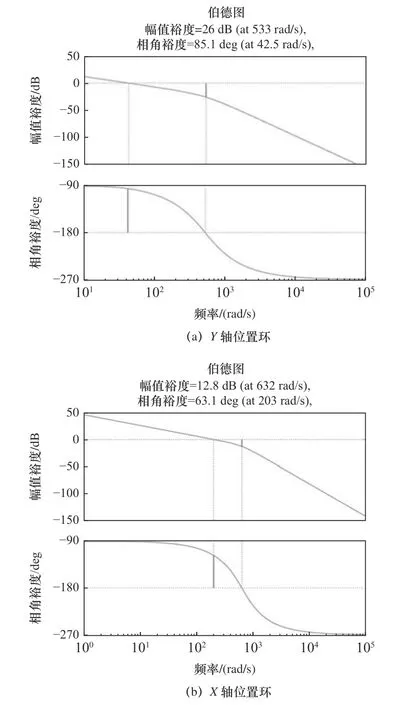
图6 位置环伯德图

4 试验研究

4.1 试验装置

以上章节已经通过伯德图稳定分析法仿真分析了二维气浮工作台控制系统的稳定性。本节将通过定位精度实验从侧面对稳定性分析结果进行试验验证。定位精度反映了目标位置与实际位置的误差，其最能反映气浮工作台的实际工况[11]。若控制系统稳定性较差，气浮工作台出现抖动以及振荡等现象，由其带来的误差会逐步叠加，从而导致定位精度较差。

定位精度试验步骤：（1）在气浮工作台各轴向先后安装固定干涉镜和反光镜。（2）调整光路使测量轴线与直线电机移动方向平行或者重合，并调整实验环境，静置24 h。（3）预热激光干涉仪，输入环境变量参数。（4）设置运动程序使气浮工作台按测量要求运动。（5）运行激光干涉仪软件，采集数据分析结果。图7 为二维气浮试验平台。

图7 二维气浮试验平台

4.2 试验结果及分析

根据国标GB/T 17421.2-2016 的规定，在X与Y轴100 mm 的行程之中选取5 个数据测量点（20 mm、40 mm、60 mm、80 mm 以及100 mm）。规划5 次往返运动程序并记录数据。目标位置轴线双向定位精度计算公式如式(25)所示。

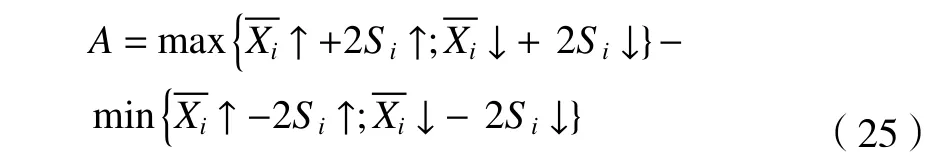
其试验结果如图8 所示。从图8 中可以看出：X轴定位精度为4.671 μm/100 mm；Y轴定位精度为2.137 μm/100 mm。试验结果表明：气浮工作台各轴向定位精度良好且在整个定位过程中，气浮工作台未出现震荡、抖动等不稳定现象。因此说明，气浮工作台拥有良好的稳定性，与仿真分析结果具有较好的一致性。

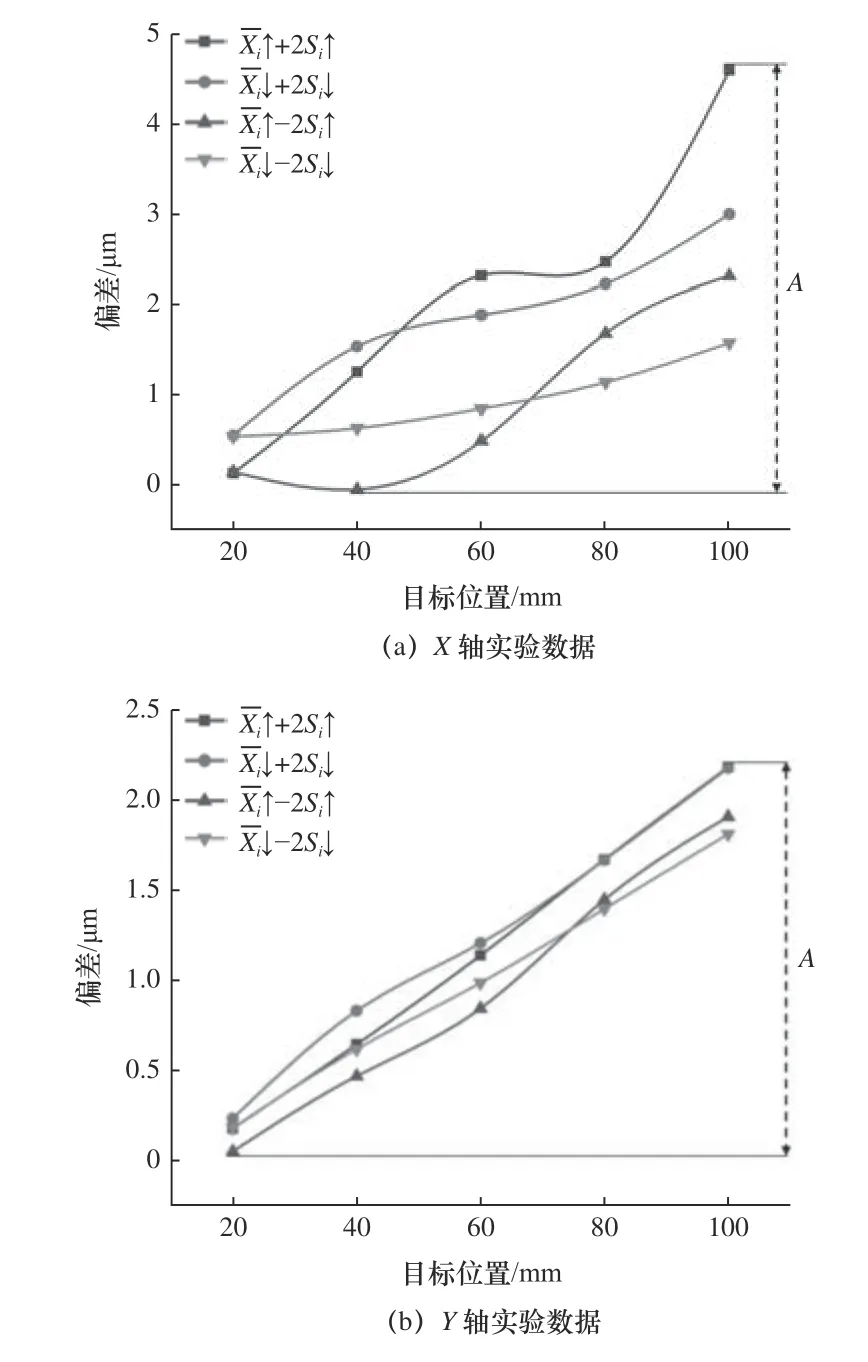
图8 定位精度实验结果

5 结语

（1）对二维气浮精密运动平台控制系统进行分析，建立了电流环为内环、速度环为中环和位置环为外环的控制模型，并推导计算各环开环传递函数，建立数学模型。

（2）利用Matlab 绘制伯德图进行仿真分析系统稳定性。Y轴与X轴电流环开环传递函数相角裕度、幅值裕度满足系统稳定裕度要求，具有足够的稳定性。速度环开环传递函数修正前，由于工作台的支撑方式导致系统的阻尼小，相角裕度及幅值裕度未达到系统稳定裕度要求，适当修改控制参数；修正后，相角裕度、幅值裕度能够满足系统稳定裕度要求。位置环开环传递函数相角裕度、幅值裕度同样满足系统稳定裕度要求。控制系统由内向外，依次分析了控制系统为稳定的，且有足够的稳定裕度。

（3）实验结果从侧面反映了仿真分析的正确性，二维精密气浮运动平台能够稳定运行，在运行过程中并未出现抖动、震荡等现象。从而验证了驱动控制系统设计的合理性，为精密气浮工作台的研制提供了研究基础。