具有固定时刻脉冲治疗策略的肿瘤免疫模型的定性分析
王 刚, 丁卫平, 张再云, 刘培宇
(湖南理工学院 数学学院, 湖南 岳阳 414006)
癌症是一种严重威胁人类生命与健康的疾病, 有效的癌症治疗策略已成为许多学者研究的焦点.传统的治疗方法(如手术切除、化疗以及药物治疗等)对癌症的治疗做出了巨大的贡献, 但是, 化疗会对免疫系统造成不可修复性的损伤, 而药物治疗会使机体产生抗药性等副作用.目前, 免疫治疗是应用最广泛的癌症治疗策略, 其通过激活机体较强的免疫效应来抑制癌细胞的增长.综合使用免疫治疗与药物治疗策略既能减轻传统治疗方法的副作用, 又能起到比单一治疗策略更好的效果.近年来, 各种各样的数学模型[1~6]被用于刻画肿瘤治疗的不同策略.本文主要考察具有固定时刻脉冲治疗策略的肿瘤免疫模型[7].该模型描述如下:

其中x为免疫细胞的数量,y为肿瘤细胞的数量,s为免疫细胞的正常输入速率,ρxy为描述免疫细胞与肿瘤细胞相互作用而促使免疫细胞产生的项,δ为免疫细胞的死亡率,α为肿瘤细胞的内禀增长率,为环境容纳量,σxy为描述免疫细胞与肿瘤细胞相互作用导致肿瘤细胞死亡的项,pE和Tp分别表示在t= (n- 1 )T+lT时刻药物对免疫细胞和肿瘤细胞的瞬时杀伤率,μ表示在t=nT时刻免疫细胞的输入量.此外,T>0表示实施脉冲治疗策略的周期, 0<l<1.
下面探究肿瘤灭绝周期解的局部稳定性及系统(1)的持久性.
1 预备知识
本节主要介绍将要用到的一些引理[8].
引理1为系统(1)的正不变集.
令y(t)≡0, 则可得到系统(1)的子系统:
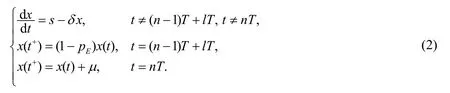
记

其中

引理2系统(1)存在唯一的肿瘤灭绝周期解 (x*(t),0), 其中
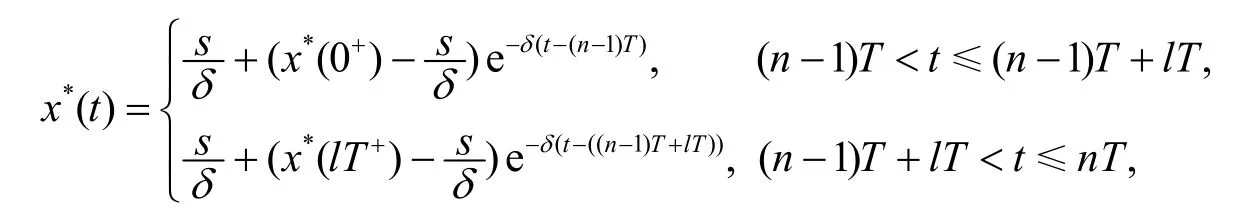
并且对系统(2)的任一解x(t)满足

引理3当时, 存在使得当t(>0)充分大时, 成立
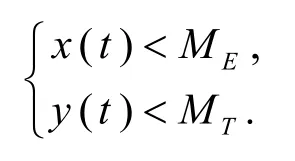
其中(x(t),y(t))为系统(1)的任一解.
2 肿瘤灭绝周期解的局部稳定性
本节主要探究肿瘤灭绝周期解局部稳定性成立的充分条件.
定理1若

则肿瘤灭绝周期解 (x*(t),0)是局部渐近稳定的.
证明令

其中(x(t),y(t))为系统(1)的任一解.
考察如下线性近似系统:
则系统(4)从t= 0+到t=T+的状态转移矩阵为
从而, Φ(T+)的特征值为
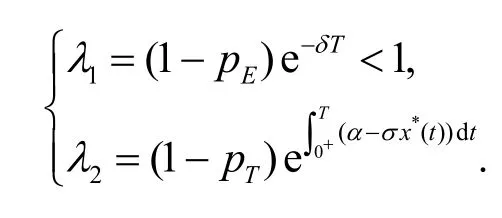
由式(3)可知, 肿瘤灭绝周期解 (x*(t),0)是局部渐近稳定的[9].
3 系统(1)的持久性
本节主要探究系统(1)持久性成立的充分条件[10].
定理2若

则系统(1)是持久的, 且存在正周期解.
证明根据引理1, 引理2和引理3可知, 存在ME,mE>0和MT> 0, 使得当t(>0)充分大时, 有

不妨设式(6)对任意t≥ 0成立.
下面证明, 存在mT> 0, 使得当t(>0)充分大时, 有y(t) ≥mT.
由式(8)和(5)可知, 存在充分小的数m0(>0)和ε2(>0)使得
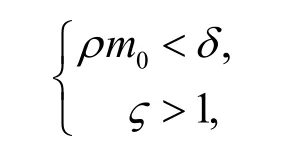
其中
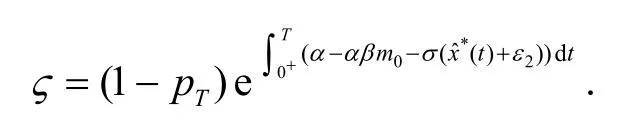
考察如下系统:

则

类似于引理2可知,

其中为系统(7)的任一解.于是, 存在t2>0,使得当t>t2时, 有
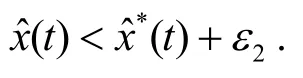
类似于(10)可证, 存在某个t3>t2,使得y(t3) >m0.
不妨设存在某个t4>t3,使得y(t4)<m0.令

则y(t*)≥m0.
进一步, 不妨设存在n1∈ℤ+,使得

且当t∈ (t*,n1T+lT]时, 有y(t)≤m0.
于是, 当t∈ (t*,n1T+lT]时, 有
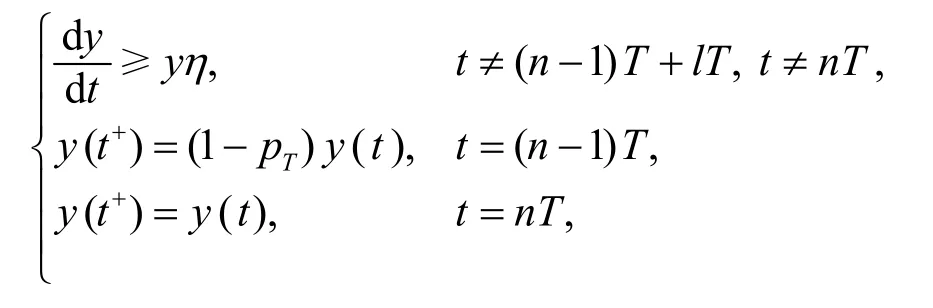
其中

从而得到
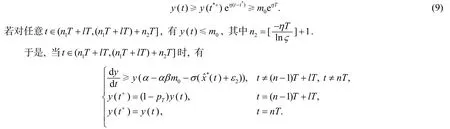
从而得到

矛盾.
故存在某个t∈ (n1T+lT,(n1T+lT) +n2T),使得y(t)>m0.
令t**= inf{t|t>t*,y(t) >m0}, 则
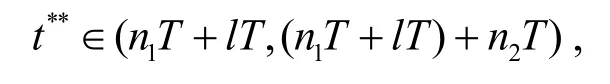
且当t∈(t*,t**]时, 有y(t)≤m0.
若存在n3∈ℤ+使得t**=n3T+lT, 则由y(t**+)<m0可知, 存在Δt>0,使得当t∈ (t**,t**+Δt) 时, 有y(t)<m0, 矛盾.于是, 由y(t)在t=t**处的连续性可知,y(t**)=m0.
对t∈ [n1T+lT,t**), 假定

其中 1 ≤n4≤n2.类似于(9)可得

对于t>t**, 上述过程可以继续进行, 这是因为y(t**)=m0.
进一步, 根据Schauder不动点定理可知, 系统(1)存在正周期解.
4 讨论
本文通过构建具有脉冲治疗策略的肿瘤免疫模型探究药物治疗与免疫治疗对肿瘤治疗动力学性质的影响, 其中药物治疗与免疫治疗策略的实施具有相同的周期但不同时进行.此外, 药物治疗能够同时杀灭常数比例的肿瘤细胞和免疫细胞.根据解对初值的可微性, 计算得到肿瘤灭绝周期解对应不动点处的雅可比矩阵的特征值, 并进一步得到其局部稳定性的充分条件.此外, 采用比较定理, 证明当式(5)成立时,系统(1)是持久的, 并存在肿瘤存在周期解.这时, 肿瘤细胞和免疫细胞能够永远共存.
图1为系统(1)关于治疗周期T的分岔图, 其中s=0.2,ρ=0.6,δ=0.8,α=0.3,β=0.01,σ=0.2,pE= 0.1,pT= 0.9,μ=0.2,l=0.5.这里, (x*(nT+),y*(nT+))表示在时刻t=nT发生脉冲之后的点.从图1可看出, 系统(1)关于治疗周期T的分岔图主要由肿瘤灭绝周期解和肿瘤存在周期解的相关动力学性质所决定.

图1 系统(1)关于治疗周期T的分岔图
图2显示了具有药物治疗与免疫治疗策略的系统(1)的动力学行为, 其中(a)(b):T=9; (c)(d):T=10.其余参数值与图1中对应的参数值相同, 且(a)~(d)中的初值均为(0.5,0.3).当T<Tp= 9.3849时, 肿瘤灭绝周期解是局部渐近稳定的(图2(a)(b)), 其中pT为肿瘤灭绝周期解的局部渐近稳定性与系统(1)的持久性的分界点.当T>Tp时, 系统(1)具有持久性, 并且出现了肿瘤存在周期解(图2(c)(d)).这时, 肿瘤灭绝周期解是不稳定的.所有的数值模拟结果表明, 合适的治疗周期T对于肿瘤的成功治疗具有至关重要的作用.

图2 具有药物治疗与免疫治疗策略的系统(1)的动力学行为

