基于三维激光扫描技术的墙面平整度评估方法*

包 胜，谢为时，叶 翔，杨 成

(1.浙江大学建筑工程学院，浙江 杭州 310058；2.杭州钱塘智慧城投资开发有限公司，浙江 杭州 310019；3.蓝城乐居建设管理集团有限公司，浙江 杭州 310016)

0 引言

建筑墙面由于表面处理工艺的局限性使最终完成表面存在凹凸和倾斜等问题，对这些问题采取有效的评估具有重要意义。墙面平整度评估作为施工质量验收的重要项目，GB 50204—2015《混凝土结构工程施工质量验收规范》提出用2m靠尺结合塞尺的方法检测墙面平整度，并且规定现浇混凝土表面平整度允许偏差<5mm。该评估方法直观便捷、操作简单，可快速获得地面、墙面不平整度值，在工程中得到广泛使用。靠尺测量是将靠尺侧面靠紧被测面，在靠尺和表面间缝隙插入楔形塞尺，塞尺最大读数即为该处表面平整度。如图1所示，对于图示2种类型的墙面，采用靠尺法检测会得到同样结果，无法有效区分2种平整度的墙面。随着墙面平整度的要求日益提高，该平整度检测方法显然无法满足要求。靠尺法存在精度差、随意性大区分度小等问题。

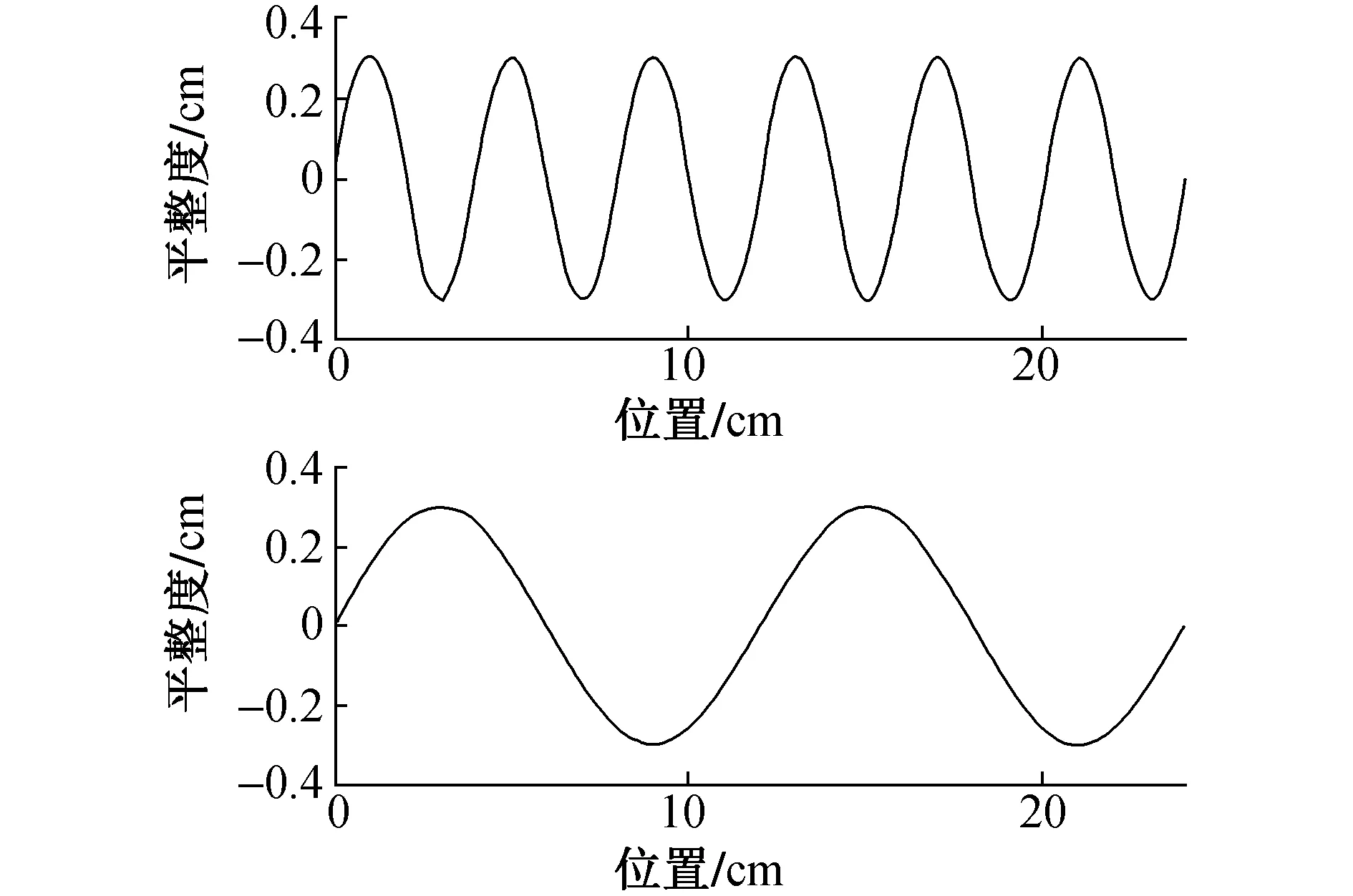
图1 不同平整度的墙面

三维激光扫描技术通过激光扫描测量方法，快速、大面积、高精度地获取待测对象的表面点云，在建筑工程变形监测[1]、结构复核[2]、缺陷检测[3]中得到广泛应用，然而针对墙面平整度的研究缺乏量化方法。李杰等[4]将该技术应用于墙面平整度评估，通过统计分析点云与墙面拟合平面距离，并与相关规范对比评估墙面平整度。王二民等[5]在去除噪声点后二次拟合平面，以重新计算的距离为准计算墙面平整度。丁克良等[6]在平面拟合方法上做出改进，将曲线拟合的线性正交距离回归法延伸到三维平面拟合中。以上平整度评估方法主要是统计分析点云与拟合平面距离，与平整度的定义存在不一致的情况。美国ASTM标准中，引入轮廓曲率概念，通过计算测量线的F值特征评估地面平整度[7]。Bosché等[8]分割点云，并在BIM模型中将点云匹配对应模型，结合靠尺法和F值法评估地面平整度。F值法被广泛应用于地坪平整度评估中，但没有对F值与平整度间相关性进行进一步研究。综上，目前对墙面平整度的研究主要集中在点云数据的处理上，包括墙面平面拟合、点云数据降噪等，关于墙面平整度的定量研究较少。本文通过分析曲率和平整度的关系，在墙面平整度评估中引入轮廓线曲率，通过从点云中提取轮廓线，计算轮廓线曲率特征W值，基于大量轮廓线的曲率特征统计结果，提出新的平整度评估方法。

1 墙面轮廓线曲率计算

图2 定位线

图3 点云剖切结果

曲率是曲线或曲面弯曲程度的度量。本研究将墙面平整度问题转化为轮廓线中曲线偏离直线程度的问题。偏离程度可通过测量点的曲率半径进行量化。曲率是曲率半径的倒数，曲率半径越大，曲率越小，代表该点附近越接近直线。

给定等间距的离散点(见图4)，点x0处的曲率qi可表示为二阶导数近似值，计算如下[9]：

(1)

(2)

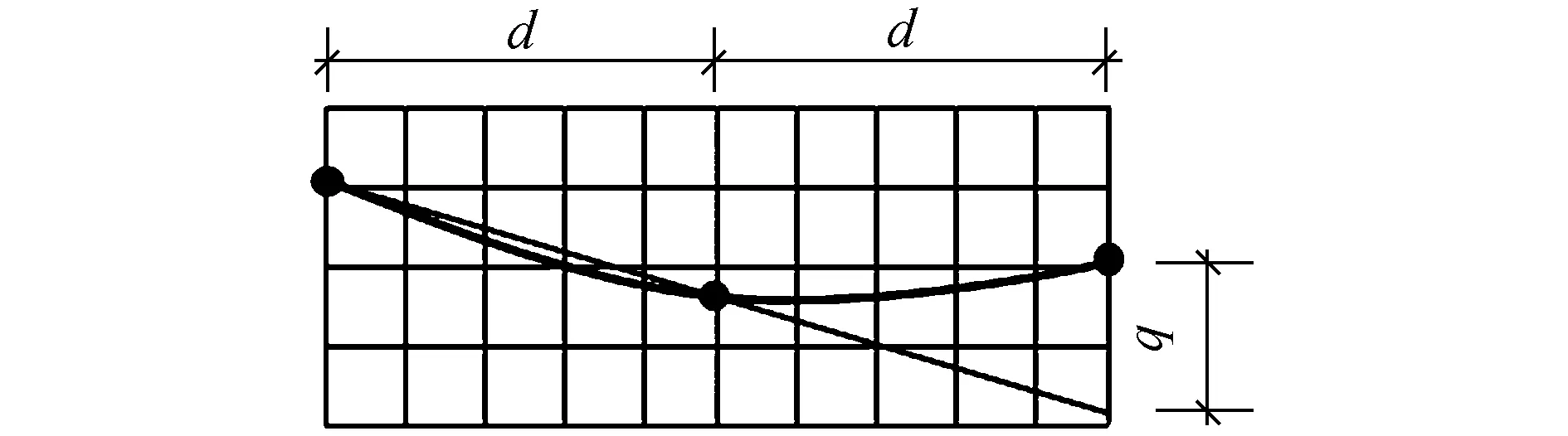
图4 等间距点曲率计算

式(1)中的最后1项是四阶误差项，对于合理的小间距值，误差项相比曲率估计值非常小。因此，式(2)近似于x0处样本轮廓线的曲率。d的取值为测量点的间距1cm，qi量纲为mm/cm2。

2 墙面平整度评估流程

本文在对墙面进行点云采集的基础上，提出基于轮廓线曲率特征的墙面平整度评估方法，包括点云数据预处理、平面拟合、墙面轮廓线提取、轮廓线曲率特征计算、曲率统计分析等，流程如图5所示。本方法首先采用Trimble TX6激光扫描仪采集墙面点云，采用Trimble Realworks对点云进行配准、着色处理、抽稀、点云清理等预处理；然后提取墙面轮廓线，在轮廓线提取过程中，通过研究墙面点云平面拟合方法、定位线选取方法、测量点计算方法，获得墙面点云轮廓线；最后得到轮廓线W值，并分析不同轮廓线W值，评估墙面不平整度。本研究主要涉及如下关键问题。

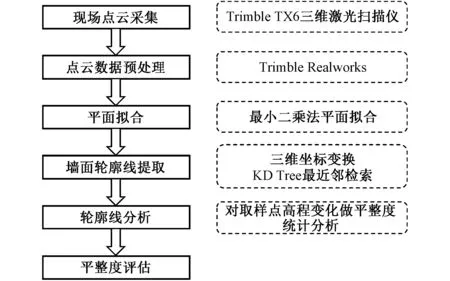
图5 评估方法流程

2.1 基于最小二乘法的平面拟合

墙面点云数据大致位于同一个平面内，通过对墙面点云数据进行平面拟合，作为轮廓线提取的参照平面，提出采用基于最小二乘法的多项式线性回归方法拟合墙面点云。

首先假设墙面点云拟合平面函数如下：

f(x,y)=Ax+By+C

(3)

计算拟合平面函数与点云中的点误差值：

|δi|=|f(xi,yi)-zi|

(4)

计算拟合平面函数与所有点的误差平方和，并求出平方和最小时拟合平面函数的A，B，C参数值，由此得到墙面拟合平面。

(5)

2.2 定位线选取

在墙面平整度W值的计算过程中，需综合考虑多条轮廓线，尽量使轮廓线分布更具代表性，因此轮廓线的位置选择至关重要。本文主要结合靠尺法和F值法的相关要求，探讨墙面轮廓线定位线确定方法。

应用靠尺检测墙面平整度，一般放置3尺，竖直1尺，顺时针、逆时针旋转45°各设置1尺，可综合考虑墙面各方向的不平整度。基于以上优点，将靠尺放置方法应用到定位线位置选取中。定位线位于拟合平面内，每个中心点放置3条定位线，均匀展示各方向轮廓，如图6所示。倾斜定位线的距离d1=10cm，竖直定位线的距离d2=14.1cm，定位线的长度可根据需要进行调整，考虑本方法最初方案来源于靠尺，与《混凝土结构工程施工质量验收规范》关系密切，定位线长度为2m。

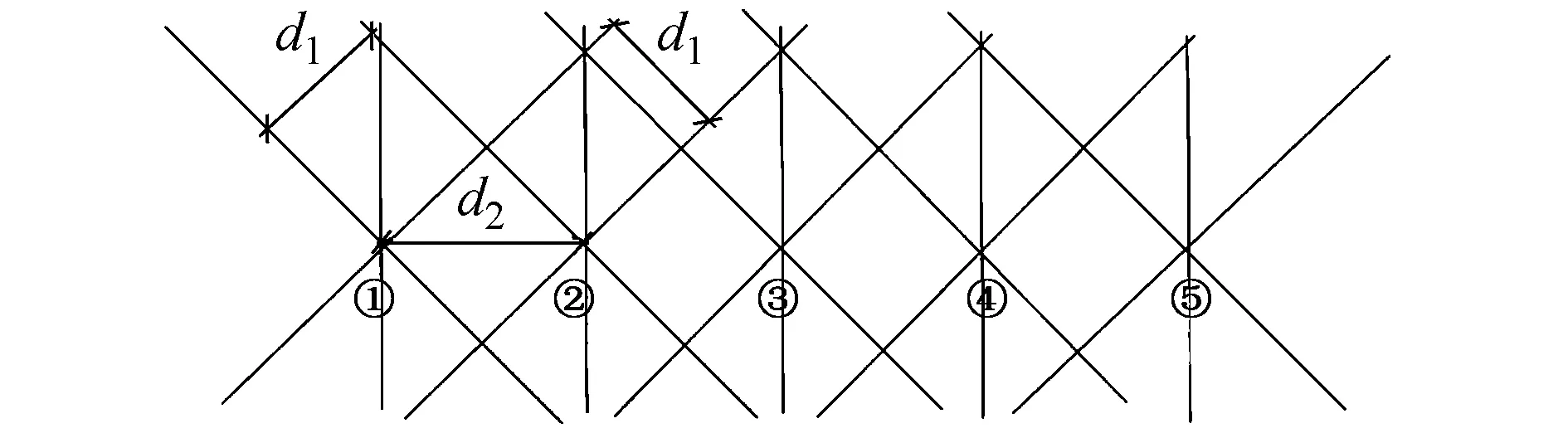
图6 定位线分布

2.3 轮廓线提取

(6)

图7 轮廓线取样

通过之前的计算可得到轮廓线上的测量点在定位线上的理论坐标，需根据理论坐标从点云中寻找深度点坐标，即寻找点云在拟合平面上的投影距离测量点投影最近的点。

已知定位线上的坐标，从点云中找出距离该点最近的一个点或多个点坐标，该过程为深度点检索过程。深度点检索的传统方法是穷举法，通过计算所有点与指定点的距离，找出最近的n个点，用n个点的坐标平均值代替该点位置，穷举法最大的缺点是当点云数量较大时，效率低。目前点云处理一般采用KD Tree最近邻检索算法进行深度点检索，采用的点检索模型是KD Tree Searcher模型，该模型基于KD Tree算法，通过将K维空间中的n个点递归地分割为二叉树，以对n·K维点云数据集进行分区，从而提高指定点检索效率[10]。KD Tree模型如图8所示。

图8 KD Tree模型

通过优化指定点的检索方法，更高效、更准确地获得轮廓线上相距1cm的深度点位置。为更直观展示轮廓线信息，以轮廓线的起始点在拟合平面上的投影点为坐标原点，沿轮廓线定位线方向为x轴方向，拟合平面法线方向作为y轴方向，重建坐标系，经过坐标重建的轮廓线，如图9所示。

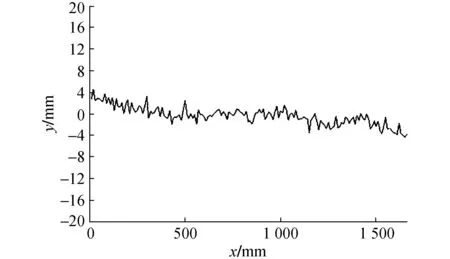
图9 坐标重建后的轮廓线

2.4 轮廓线W值计算

轮廓线上某点的曲率可描述该点前后的平整度，曲率标准差表示轮廓线上不同位置平整度的不均匀性，即表示轮廓线位置的墙面不平整度。

如图10所示，每个测量点相对拟合平面高程为hi，通过下式计算轮廓线曲率：

qi=hi-1-2hi+hi+1

(7)

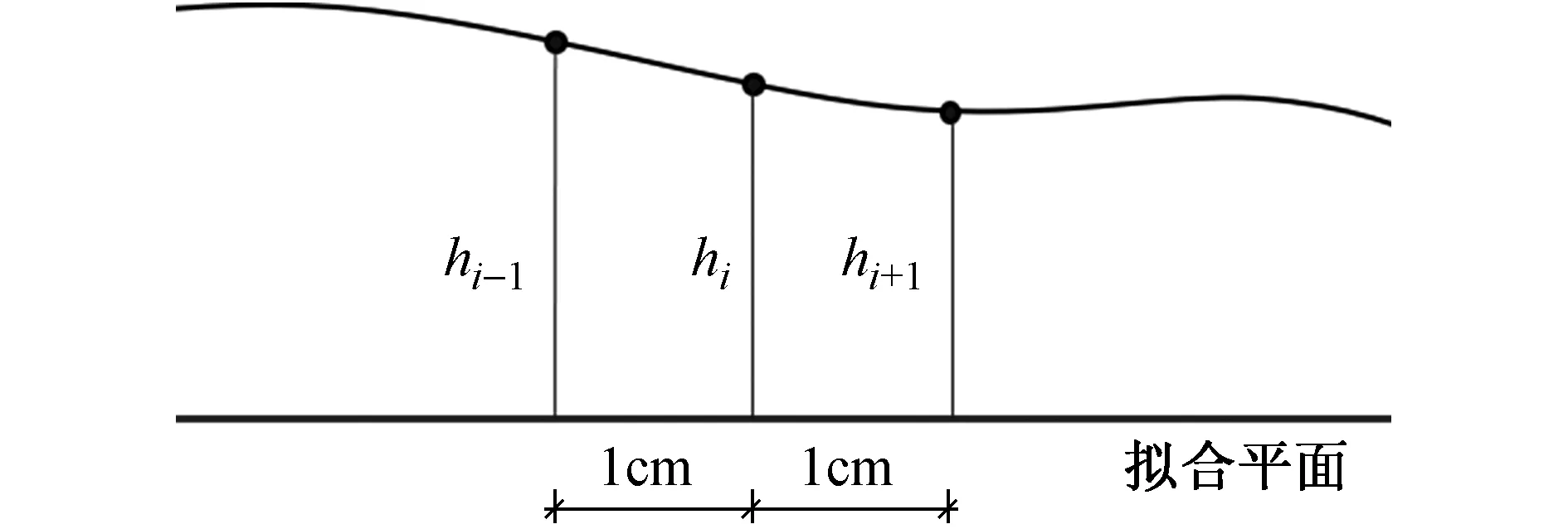
图10 轮廓线局部示意

通过下式计算曲率标准差：

(8)

曲率标准差越大，平整度越低。提出采用标准差的倒数乘以放大系数作为平整度评价指标W，放大系数沿用ASTM标准中W值法的系数。

(9)

轮廓线曲率为qi，为正值时代表i点处于轮廓线的谷点，为负值时代表i点处于轮廓线峰点。轮廓线曲率标准差为Sq，标准差直接决定墙面平整度W值。

3 案例分析

为评估本方法的有效性，选择浙江大学某新建教学楼3处位置的墙面进行分析，每面墙按描述的方法提取100条轮廓线并计算W值。三面墙的W值分布统计如图11所示。每面墙的W值统计结果呈中间高两边低的形式，W值主要集中在平均值附近。

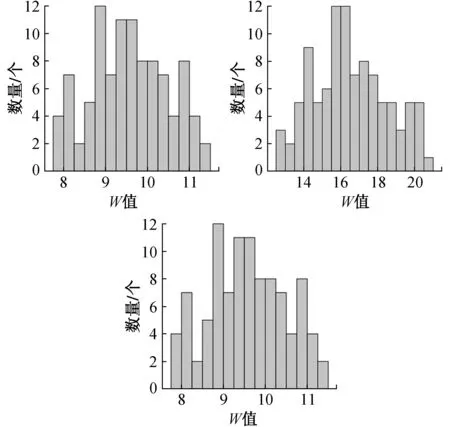
图11 三面墙W值分布

每条轮廓线的W值都是墙面整体W值的随机样本。为验证样本数据是否来自正态分布，对样本数据进行正态性验证，常用检验方法有柯尔莫戈洛夫-斯米诺夫检验法和夏皮洛-威尔克检验法。原假设H为样本数据，与正态分布无显著差别，显著性水平为0.05。通过SPSS对样本数据进行正态性检验，计算所得结果如表1所示，显著性水平均>0.05，不能拒绝原假设，即认为数据服从正态分布。SPSS同时计算样本数据的统计数据特征，如表2所示。

表1 正态性检验结果

表2 参数估计结果

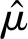
(10)

(11)

采用参数估计方法对三面墙的总体W值进行估计，结果如表2所示，样本平均值估计结果表明内墙2>内墙1>乳胶漆外墙。即外墙属于乳胶漆墙面，表面存在许多颗粒，因此W值较低，平整度较差。参与评估的两面内墙选取部位不同，材料与工艺相同，W值相近，且大于乳胶漆外墙。置信区间描述该区间包含墙面真实W值的概率，以内墙1为例，95%置信区间为[15.4,16.1]，即墙面真实W值在该区间内的概率为95%。相比点估计，区间估计允许W值估计有一定弹性区间，与墙面平整度在一定范围内存在波动符合。

4 结语

本文通过Matlab编程从墙面点云中提取表面轮廓线，计算轮廓线曲率特征，并提出反映墙面平整度的W值。W值的有效性在浙江大学某新建教学楼的墙面平整度评估中得到验证。在利用三维激光扫描数据进行平整度评估过程中，得出以下结论。

1)相比传统方法统计分析墙面点云与拟合平面距离，本法提出用轮廓线的曲率特征表征墙面平整度具有更深的理论背景，结合Matlab编程，从点云中提取轮廓线具有自动化程度高、整体性强的优点，提升墙面平整度评估的准确性和效率。

2)通过统计分析三面墙的100条轮廓线W值，得出每面墙的轮廓线W值服从正态分布规律的结论。基于样本和整体关系，根据样本轮廓线W值对墙面总体W值进行估计是有效的，并可作为墙面平整度评估依据。

三维激光扫描技术应用到墙面平整度检测是发展的趋势，在平整度评估理论上做了改进。本文测量点的间距为1cm，W值计算公式中放大系数沿用ASTM标准，今后的研究中需要关注不同测量点间距对W值的影响，同时将本法应用到不同类型的墙面中，提出最优放大系数，以区分不同平整度的墙面。