基于航迹数据的油耗分析与研究

陈昱君，孙樊荣，许学吉，沐 瑶

（南京航空航天大学民航学院，南京 211100）

在民航业蓬勃发展的背景下，中国航空公司的盈利情况却不甚良好，其中，燃油正是制约航空公司（简称航司）盈利的重要因素之一。为了提高燃油利用效率，促进航司盈利，需要更加精准地计算飞机携带燃油量。在雷达管制十分普及的情况下，航空器不再按照传统的进离场程序飞行，而是在一定空域范围内受管制员指挥，不同管制员的管制方式会形成不同的飞行路径，造成了以往按照程序计算燃油消耗（简称油耗）的方式不再精准。综上所述，基于航迹数据进行油耗分析与研究对提升航空公司的运行效益有着重要意义。

在飞机油耗的计算方面，国内外学者已经进行了大量研究。在国外，Khadilkar 等[1]利用飞行数据记录器的数据，基于最小二乘回归法以滑行时间、停车次数、转弯次数和加速活动4 个变量建立了两个线性模型对航空器滑行阶段的油耗进行预测；Lawrance 等[2]通过对高斯过程回归、K-近邻回归、简单线性、新的基于空气动力学的4 种模型采用高频数据计算不同阶段的K值并进行对比，结果表明新的基于空气动力学的模型计算油耗更加精确；Oh 等[3]将地面燃油消耗与发动机推力状态相关联，且发动机推力状态根据地面停车状况的不同可分为峰值状态和常规状态，因此可通过国际民用航空组织（ICAO，International Civil Avi-ation Organization）数据库建立基于停车转弯的地面油耗模型与基于加速的地面油耗模型，并将这两种模型的计算结果与QAR（quick access recorder）数据对比，结果显示加速运动才是影响飞机滑行阶段油耗的因素。在国内：赵冬林[4]利用Pearson 系数进行相关性分析，结合真实的QAR 数据分析了航行滑出、滑入、爬升、巡航、下降5 个阶段油耗与影响因素的关系，并建立了基于支持向量机的油耗模型，粗略地计算了下降阶段的油耗，但忽略了进近阶段的油耗；钱宇等[5]利用一元线性回归分析方法对QAR 滑行时间数据进行拟合，提高了滑行时间的预测精度，从而对油耗计算进行优化，但其只考虑了滑行时间一个影响因素，对于滑行时具体油耗估算并不准确；黄倩文等[6]基于BADA（user manual for the based of aircraft data）油耗模型，结合QAR 数据采用最小二乘法拟合气动参数中的升力系数和阻力系数，并同时考虑侧风的影响对离场油耗模型进行了优化，其计算精度高于风洞计算。

在航迹数据处理方面：Gariel 等[7]利用基于雷达数据的K-means 算法，对终端区航迹进行聚类分析，有效地实现了对航空器的实时监控；王莉莉等[8]利用局部异常因子（LOF，local outlier factor）算法对航迹点的局部可达性密度进行计算，对大于1 的航迹点进行野点甄别和排除；陈勇[9]通过line-segment-clustering 算法对每条航迹邻域范围内航迹数量小于阈值的航迹进行剔除；韩云祥[10]基于航空器物理运动的6 个参量建立连续动态模型，并结合飞行管理系统航路点的8个离散变量建立离散切换模型，然后通过Petri 网进行融合，并加入风场变量插值，从而拟合出航迹飞行的高度剖面和水平剖面；何艳等[11]利用均值及合成航迹线的思想对现有的航迹数据特征进行总结，并提出基于航迹形状约束的半监督K-means 算法对航迹进行聚类。

通过对上述研究总结发现：①计算航空器油耗的方式多种多样，而基于BADA 数据库进行油耗计算是被广泛采用和认可的一种方法；②利用QAR 数据分析航行各个阶段油耗已日益完善和精细，能够对航行各个阶段进行详细的动态分析计算，但下降进近阶段由于雷达管制的普及，各个管制员的指挥方式相差较大，飞机的飞行轨迹差异大，对飞机的油耗影响不可忽略；③现阶段研究都是从单个航空公司的QAR 数据库进行分析，缺少来自空管雷达全部数据的综合分析，存在一定的单一性和片面性。

针对上述研究的不足，提出采用BADA 数据库提供的燃油计算方法，搭建下降进近阶段的油耗模型，并通过大量的空管航迹数据计算油耗，对计算结果进行假设检验，分析燃油分布特点并计算出航司燃油携带建议值。

1 航迹数据处理

空中交通雷达航迹数据记录了航空器航行的诸项元素，但由于获取到的数据杂乱且存在异常数据以及缺失数据，为了能够精准地计算油耗从而为航司提供科学的决策量，在利用雷达航迹数据进行油耗计算前，要对纷繁复杂的航迹数据进行分析和处理[12]。

1.1 航迹数据分析

一条完整的雷达航迹由若干个航迹段组成，而每个航迹段又是由单个孤立的航迹点构成。从集合的角度看一条航迹表示为D={R1，R2，…，Rn}，其中，n 为航迹段个数，Ri为第i 个航迹段，Ri={p1，p2，…，pm}，表示该条航迹段由m 个航迹点组成，每个航迹点按照时间序列依次排列，由于航迹段长度不同，航迹点的个数也不相同。pj={t，la，lo，h，f，v}，表示第j 个航迹点是由以下6 项航行元素定义的：t 表示航空器位于该点的时间，la表示该点的纬度，lo表示该点的经度，h 表示高度，f 表示航向，v 表示航空器的速度。

总而言之，航迹由航迹段构成，航迹段是计算燃油的基础单位，航迹段由若干个航迹点组成，每个航迹点的时间间隔为雷达波束的扫描间隔即4 s，而每个航迹点又是由6 项航行元素表征的。

1.2 航迹数据处理

由于获取到的雷达数据是杂乱的，要想在海量的数据中提取有效因素进行油耗分析，首先要对数据进行规范化处理，即将原始数据可视化；由于研究范围为进近阶段，所以对原始数据进行范围提取；由于雷达有一定容错率，难免会有噪声和缺失，所以对数据离群点进行剔除，并为了计算的连贯性利用插值法补全数据；最后进行特征点提取，即针对每条航迹进行拐点识别，从而对航迹分段来计算携带燃油消耗量[13]。航迹数据处理流程，如图1 所示。

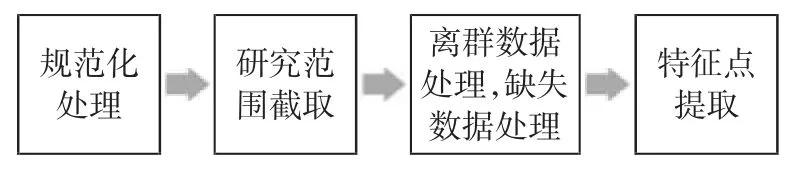
图1 航迹数据处理流程Fig.1 Trajectory data processing process

1）规范化处理

用Python 对原始数据进行规范化处理，以期得到规整的.csv 格式文件，读取excel 形式的.csv 数据文件，查看整体数据。

2）研究范围截取

由于获取到的航迹数据是整个管制区域的全部航迹数据，为了只保留计算所需数值，截取起始值为开始下降的高度，终止值为QFE（query field elevation）100 m。

3）离群数据和缺失数据处理

雷达数据中常含有噪声和错误数据，常见的错误类型有数据突变和数据缺失。若时间、速度和高度有异常或缺失值则删除整行数据。

航迹截取和异常数据处理流程如图2 所示。

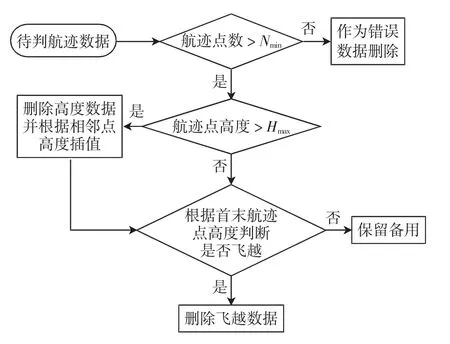
图2 航迹截取和异常数据处理流程图Fig.2 Flow chart of trajectory interception and abnormal data processing

图2 中，航迹中航迹点最小Nmin=500，即当航迹点数少于500 时，将该条航迹作为错误数据删除，航迹点最大高度Hmax=8 000 m，即文中只考虑8 000 m以下的进离场航班。

4）特征点提取

特征点是指高度改变的点。由于航空器在空中飞行难免遇到颠簸对高度产生影响，航空器处于平飞阶段期间，雷达数据的高度显示很难一成不变，所以通过观察20 组进近航迹数据平飞阶段各个点的高度误差，计算得出平飞阶段每相邻两个航迹点允许10 m 以内的高度容差。在特征点的提取中也基于10 m 容差范围对数据抖动情况进行排除，即满足if data[i+1]-data[i]<-10 or if data[i]-data[i+1]<-10，则可视为data[i+1]=data[i]。对每条航迹进行分析，采用相邻3点检查，检查某个点与其相邻前后两点高度的大小关系，判断该点是否为拐点。若检查结果满足data[i-1]=data[i]and data[i+1] data [i] and data[i+1]=data[i]，则数据i 为下降转平飞的拐点。如此反复可得到所有特征点。

2 基于BADA 数据库的油耗计算模型

BADA 数据库关于某机型发动机的油耗模型是利用机型性能参数表获得航空器在平飞阶段和下降阶段的燃油消耗系数及推力系数，从而获得单位时间内的燃油消耗率[14]，再结合雷达数据给出的航迹点时间信息得到航迹数据对应的燃油消耗量。

2.1 推力计算方法

2.1.1 最大爬升推力模型

1）标准大气条件下的计算模型

最大爬升推力是计算各个阶段推力的基础，而最大爬升推力是根据真空速、标准海平面气压高度和温差计算的。以下给出各类发动机在标准大气（ISA，international standard atmosphere）条件下的最大爬升推力模型，分别给出各类型单台发动机（ISA 条件下）最大爬升推力计算公式。

涡喷式

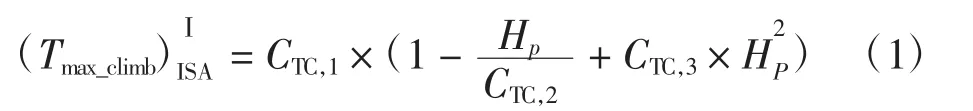
涡桨式

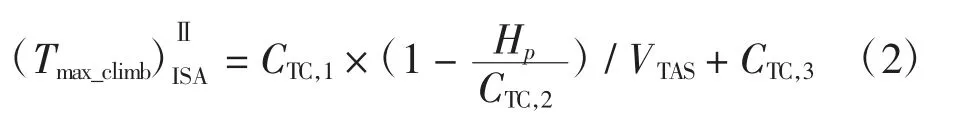
活塞式

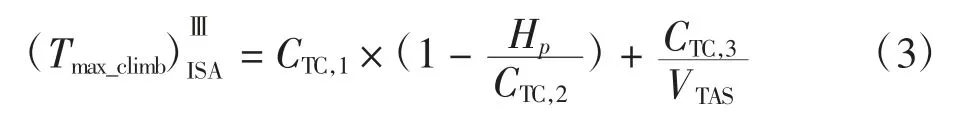
式中：CTC，1、CTC，2、CTC，3为推力系数，由机型决定；Hp为标准海平面气压高度（1 ft=0.340 8 m），取航段开始高度；VTAS为真空速（1 kn=1.852 km/h），取航段平均值。

2）基于温度修正的计算模型

在航空器实际运行过程中，由于高度或气候等因素改变，运行外界温度不可能一成不变。而温度变化对发动机推力也会产生影响，因此给出了在实际大气温度条件下3 类发动机的最大爬升推力的温度修正表达式。

实际大气条件下的单台发动机最大爬升推力为

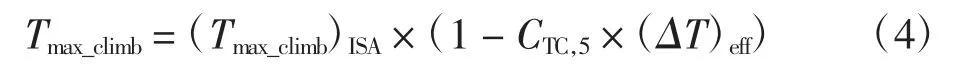
式中（ΔT）eff为基于温差的修正量，其修正方式为

最大爬升推力模型的约束条件为

式中：CTC，4、CTC，5为推力系数，由机型决定；ΔT 为实际大气温度与ISA 的差值（℃）。

2.1.2 平飞阶段推力模型

根据定义，平飞阶段推力等于阻力。然而真实运行过程中可用的最大推力是有限的。因此，实际运行过程中的最大平飞推力以最大爬升推力和相应的推力系数得出。

平飞阶段的推力模型为

式中：（Tcr）max为平飞阶段中单台发动机的最大推力（kN）；CTr为最大平飞推力系数，由机型决定，无量纲。

2.1.3 下降阶段推力模型

下降阶段的推力表达式根据高高度下降、低高度下降、进近形态和着陆形态采用不同的修正系数，但所用的计算方式相同，在公式中统一用j 指代飞行阶段，其表达式如下

式中：Tdes，j为第j 下降阶段推力（kN）；CTdes，j为第j 下降阶段推力系数。

由于不同下降阶段对应的推力大小相差很大，所以BADA 数据库关于CTdes，j的取值根据高度和飞行阶段的不同给出以下4 种情况，如表1 所示，其中：Hdes为下降阶段的参考高度（ft），Ht为航空器当前飞行高度（ft）。

表1 下降时推力系数与推力对应表Tab.1 Correspondence table of thrust and its co-efficiency when descending

2.2 平飞阶段燃油消耗率

平飞阶段的燃油消耗率采用的是标准燃油流量，是关于推力油耗比和推力的表达，适用于除了巡航和慢车推力状态的各个阶段[15]。其中，单位时间单位推力的油耗是关于VTAS的函数，根据发动机类型的不同其表达式也不同。

1）涡喷式、涡桨式发动机燃油消耗率

式中：fnom为标称燃油消耗率（kg·min-1）；THR为平飞阶段的推力（kN）；η 为单位时间单位推力的燃油消耗量（kg·min-1·kN-1），分为以下两种计算方式。

a）涡喷式发动机

式中Cf1，Cf2为第一单位推力燃油消耗系数。

b）涡桨式发动机

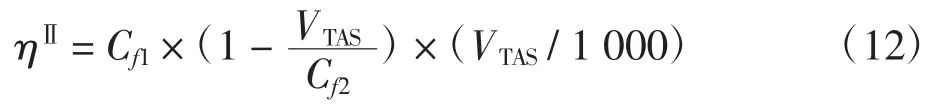
2）活塞式发动机燃油消耗率

2.3 下降阶段燃油消耗率

1）涡喷式、涡桨式发动机燃油消耗率

根据BADA 数据库，对于喷气发动机和涡轮螺旋桨发动机，当飞机切换到下降形态，尤其是进近和着陆时，下降的推力部分停止[16]。因此，进近和着陆阶段的燃料流量计算应以标准燃料流量为基础，并在必要时限于最小燃料流量。也就是说，下降阶段的燃油消耗率fdes应当以标准燃油消耗率和最小燃油消耗率的最大值为准，即

式中：fnom与上一节提到的计算方法一致；fmin为最小燃油消耗率，计算方式如下

2）活塞式发动机燃油消耗率

与活塞式发动机的下降条件相对应的燃油流量规定为该机型的最小燃油流量也即fmin，此参数规定为一个常数，该常数由飞机的机型决定，即

式中fdes为下降阶段燃油消耗率（kg·min-1）。

2.4 油耗计算模型

在假定各个航迹段燃油消耗率恒定的情况下，利用上述燃油消耗率模型及雷达数据中的时间、速度和高度信息对某条航迹的油耗进行计算。

由图3 可见，一条下降航迹由若干个平飞阶段和下降阶段组成。每个阶段的油耗等于燃油消耗率与时间的乘积，其中不同机型不同阶段的燃油消耗率的计算方式已在第2 节的前述部分给出，每个航段的时间在识别航迹数据的特征点后也可直接得出，最后将平飞阶段和下降阶段的油耗叠加组合计算得出航空器下降进近阶段所需的油耗总量。

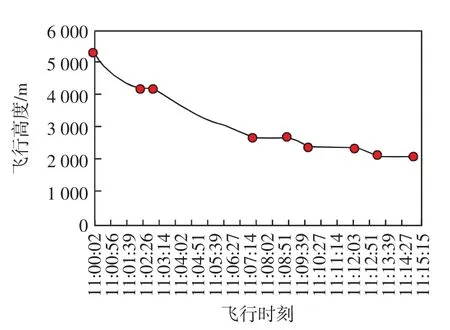
图3 下降进近航迹Fig.3 Descent approach trajectory

若某一条下降进近航迹命名为d，其由x 个平飞阶段和y 个下降阶段组成，每个航段的燃油消耗率保持不变，结合2.2 和2.3 中提出的计算方式，其油耗总量计算模型如下

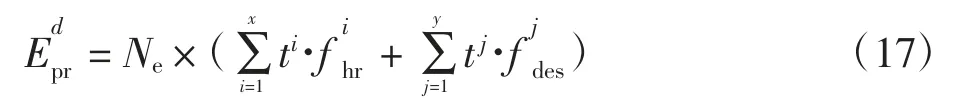
式中：Ne为航空器发动机数量；ti、tj为第i 平飞阶段和第j 下降阶段的持续时间（min）为第i 平飞阶段燃油消耗率（kg/min）为第j 下降阶段燃油消耗率（kg/min）。

3 算例分析

3.1 基于BADA 数据库的油耗计算

3.1.1 数据介绍

1）航迹数据

采用中国民用航空西南地区空中交通管理局云南分局提供的30 d 中同一时段11：00—12：00 之间进近阶段的航迹数据作为研究对象，验证所提出的进近阶段的油耗计算模型及油耗数据分析方法的可行性和有效性。

2）机型数据

将依据采集的雷达数据进行油耗计算，经数据筛选共涉及4 种机型，在BADA 数据库中找到这些机型的性能参数，并摘录其相应的计算推力和油耗的参数，如表2 所示。

表2 各机型油耗参数表Tab.2 Fuel consumption of each type of plane

3.1.2 单条航迹算例验证

图4 为某架B737-800 的进近航迹示意图，其进近开始高度为10 394 ft，进近结束高度为2 469 ft，共分为2 个平飞阶段和3 个下降阶段，公式中的高度采用各个航段的起始高度，真空速采用航段平均速度。按照第2 节给出的计算模型进行计算如表3 所示。

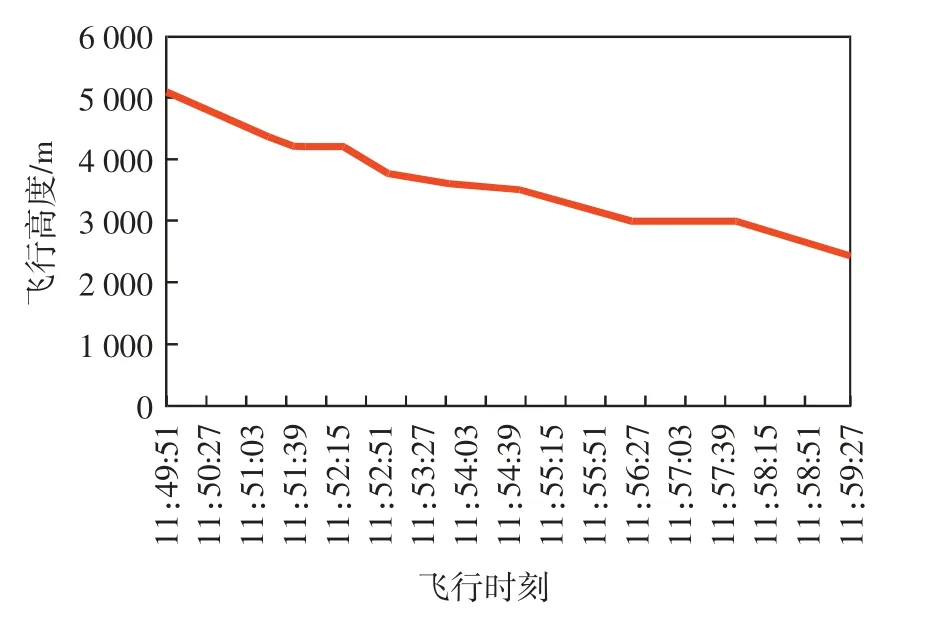
图4 某架B737-800 进近航迹图Fig.4 Approach trajectory chart of a B737-800

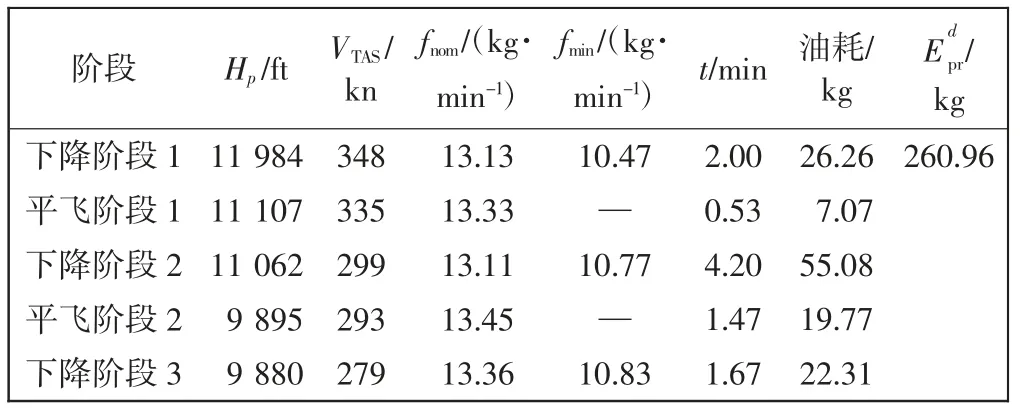
表3 B737-800 进近航迹油耗计算Tab.3 Fuel consumption calculation of an approaching B737-800

3.1.3 科学燃油决策量

利用SPSS 对各机型的油耗数据进行分析，计算自由度df 和显著性P 值，如表4 所示，观察其显著性检测的P 值均大于0.05，可以发现各机型油耗均服从正态分布。再以某架B737-800 为例进行进一步验证，其Q-Q 图如图5 所示。由图5 可见，油耗数据的分布非常接近于一条直线，因此确定B737-800 机型在同一时段的进近阶段的油耗服从正态分布，假设成立。通过分析其余各个机型Q-Q 图也均满足条件，不再赘述。

图5 B737-800 油耗Q-Q 图Fig.5 Q-Q diagram of B737-800 fuel consumption

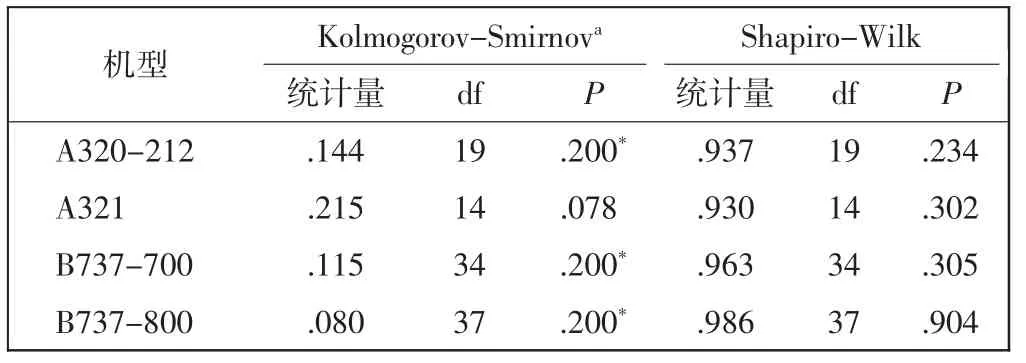
表4 各机型SPSS 正态性检验表Tab.4 SPSS normal test table of each type of plane

在验证飞机油耗符合正态分布后，利用SPSS 进行双边95%置信度检验，得到各个机型的均值的95%置信区间的上限值，该值为满足昆明长水国际机场航班进近阶段95%情况下足够用油的科学燃油决策量。其计算结果如表5 所示。

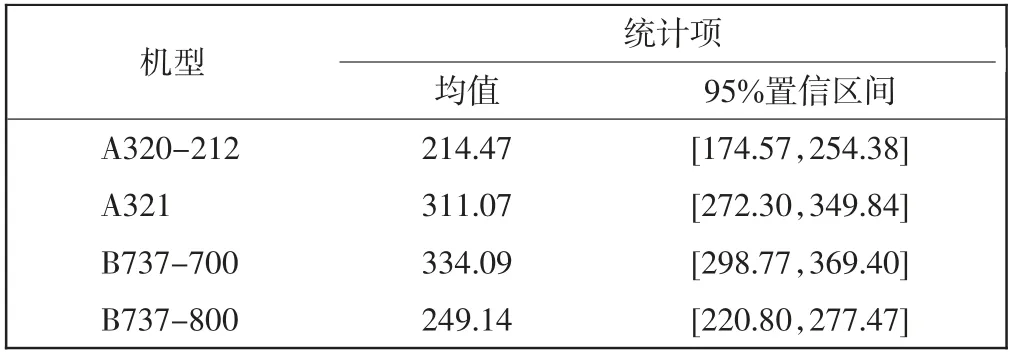
表5 各机型正态分布分析结果Tab.5 Analysis results of normal distribution of each type of plane

3.2 基于进近程序的油耗计算

以昆明长水国际机场IDPUG 进近程序为例进行计算。起始进近定位点高度为11 800 ft，中间进近定位点高度为10 800 ft，中间进近至最后进近为平飞阶段，进近结束高度为机场标高之上2 000 ft，即8 901 ft，平均速度采用进近标准速度。基于IDPUG 进近程序设计的进近轨迹，可知飞机飞行的航段计算高度、航段长度、平均速度和航段持续时间，结合飞机飞行的油耗计算模型（式（17））可得出各型号飞机在进近阶段需要的油耗总量。

进近程序各阶段的基本飞行情况如表6 所示。

将表6 中的各飞行阶段的燃油消耗率与航段持续时间相乘，然后求和得到各机型在进近阶段的油耗。分别列出基于IDPUG 进近程序计算的油耗及通过大量航迹数据计算燃油携带建议值的对比，以及所计算的航迹数据的平均进近时间，如表7 所示。

表6 IDPUG 进近程序各阶段基本飞行情况Tab.6 Basic flight conditions at each stage of the IDPUG approach procedure

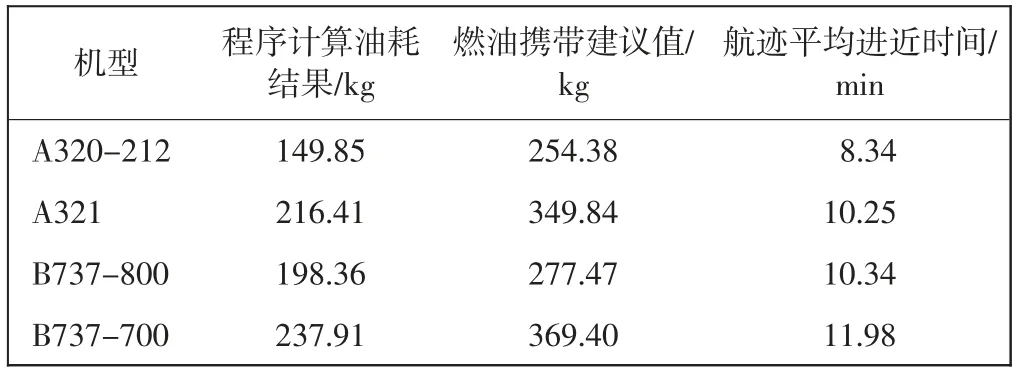
表7 油耗对比Tab.7 Comparison of fuel consumption

3.3 计算结果对比分析

通过3.1 和3.2 的油耗计算结果可以直观地看出，基于航迹数据所计算的油耗建议值大大超出基于程序计算的结果，主要原因如下。

1）进近时间和路径差异大

由于雷达管制普及，航空器进近轨迹不再完全按照进近程序进场着陆，例如基于程序推算的进近时间大约为7 min，而所有雷达数据中的进近航迹的平均进近时间都已经全部超过这个数值，由此可见在雷达管制下路径的不确定性对飞机油耗的影响较大。

2）终端空域航空器相互之间影响大

随着航空器数量的日益增加，排队和等待的现象也日趋常见，基于航迹数据的油耗计算采用的是同一时段内连续进近的航空器油耗数据，而基于进近程序计算时却无法考虑航空器之间的间隔造成的额外航空器油耗。

3）航迹数据计算基于实际大气环境

风向、风速和气温均是影响航空器油耗的因素，基于航迹数据进行油耗计算时，航空器的速度是受风影响的真实速度，而基于程序的计算则是采用进近图中推荐的理想速度所得出的数据，忽略了自然因素对航空器油耗造成的影响。

综上所述，基于进近程序对油耗进行预测不再适用于当前的运行控制，从而更加凸显对于同一机场、同一机型基于大量雷达航迹数据进行油耗预估的可信度。

4 结语

基于航迹数据的燃油消耗率计算方法可得到科学客观的航空器燃油携带量，给航空公司决策航空器燃油携带量提供了有力的参考。为保证研究的客观性，采集实际航迹数据，对航迹数据进行处理与分析，采用BADA 数据库的油耗计算方式计算得出航空器下降进近阶段的实际油耗，并给出建议携带燃油量，计算结果贴合实际，更适用于雷达管制已普及的现代航空运输规划。但目前只研究了下降进近阶段的油耗，整个飞行阶段更精确的油耗计算需要进一步的研究。