Interval-Valued Neutrosophic Soft Expert Set from Real Space to Complex Space

Faisal Al-Sharqi，Abd Ghafur Ahmadand Ashraf Al-Quran

1Department of Mathematical Sciences，Faculty of Science and Technology，Universiti Kebangsaan Malaysia，Bangi，Selangor，43600，Malaysia

2Department of Mathematics，Faculty of Education for Pure Sciences，University of Anbar，Ramadi，55431，Iraq

3Preparatory Year Deanship，King Faisal University，Hofuf，Al-Ahsa，31982，Saudi Arabia

ABSTRACT A fuzzy system is a novel computing technique that accesses uncertain information by fuzzy representation.In the decision-making process，fuzzy system and soft computing are effective tools that are tolerant to imprecision，uncertainty，and partial truths.Evolutionary fuzzy systems have been developed with the appearance of interval fuzzy，dual fuzzy，hesitant fuzzy，neutrosophic，plithogenic representations，etc.Moreover，by capturing compound features and convey multi-dimensional data，complex numbers are utilized to generalize fuzzy and neutrosophic fuzzy sets.In this paper，a representation of neutrosophic soft expert systems based on the real and complex numbers in the interval form is proposed.The interval-valued neutrosophic soft expert set(I-VNSES)is defined，and the interval-valued complex neutrosophic soft expert set(I-VCNSES)is formally generalized from the concept of IVNSES.For both I-VNSES and I-VCNSES，we introduce the relevant basic theoretical operations and study their properties.Based on these new concepts，a generalized algorithm is proposed and applied to handle the imbedded indeterminacy in the two-dimensional interval data.The proposed algorithm is tested on the economic factors that affected the Malaysian economy in 2020 to see which ones are the most influential.Eventually，a comparison of three current approaches is used to back up this study.

KEYWORDS Interval-valued neutrosophic set;complex neutrosophic set;interval-valued complex neutrosophic set;soft expert set;decision making

1 Introduction

Fuzzy sets [1] and its extensions，such as intuitionistic fuzzy sets [2] and neutrosophic sets [3]，have provided a wide range of tools that can deal with uncertainty in different types of problems.The neutrosophic set has become increasingly popular in the last two decades as a sophisticated representation of uncertain，incomplete and undetermined data.The neutrosophic set(NS)is characterized by three membership functions which represent truth，falsity，and indeterminacy，and all these three memberships take values in the non-standard interval[0-，1+].Smarandache[4]and Wang et al.[5] introduced the single-valued neutrosophic set(SVNS)as a result of the fast growth of neutrosophic theory，and this set was later included in various decision-making methods[6-11].The SVNS is modified from the classical neutrosophic set which membership structure is similar to the original model.Still，all of these membership functions take on values between 0 and 1.In reality，the degree of truth，falsehood，and indeterminacy of a statement might occasionally be expressed by various different interval values rather than being specified precisely in real situations.So，the idea of interval neutrosophic set(INS)was proposed by Wang et al.[12] and gave the set-theoretic operators of INS.Multi-criteria decision-making(MCDM)is one popular branch of decision-making theory and has been extensively studied in numerous researches[13-20].Decision information is often incomplete，inconsistent，and undetermined，which further complicates the decision-making process.Therefore，the process of integrating the aforementioned uncertainty sets with the MCDM technique has attracted the attention of many researchers.This useful contribution leads to a fruitful output in the relevant research literature[21-26].On the other hand，in some situations，we need to express some real data of two dimensions，which cannot be expressed by the models mentioned above，which heightens the need for developing several improved hybrid models that can deal effectively with this type of data.Consequently，complex numbers are utilized to generalize fuzzy sets through complex fuzzy set[27]by Ramot et al.Complex fuzzy set is characterized by a unique membership function which consists of two terms called amplitude term and phase term，where the amplitude term handles the uncertainty，and the phase term represents the periodicity.This，in turn，led to the development of many similar models.The most commonly used one which is relevant to this research is the complex neutrosophic set by Ali et al.[28].A complex neutrosophic set is characterized by three membership functions，each of which consists of amplitude term and phase term.The amplitude terms of the truthiness，falsity and indeterminacy in a complex neutrosophic set are analogous to the membership，non-membership and indeterminate membership functions in a single-valued neutrosophic set.In contrast，the phase terms expressed the periodicity of the information.Thus，complex neutrosophic sets handle the single-valued neutrosophic data，which have the periodic manner.In many real-life applications，it is not easy to find a crisp(exact)neutrosophic membership degree(as in the single-valued neutrosophic set)since we deal with unclear and vague periodic information.To overcome this，Ali et al.proposed an interval complex neutrosophic set(ICNS)[29].On the other hand，the theory of soft set[30]has been initiated to handle uncertainty but with the construction that differs from other constructions as in the other uncertainty sets.It is a mapping that attaches each parameter from its domain to a subset from the universal set.Since its inception，the soft set has achieved a widespread as a powerful tool that represents complex variables in a systematic way to handle uncertainty.Accordingly，it has been incorporated into other uncertainty sets to improve their efficiency.In addition，Alkhazaleh et al.introduced a more advanced form of a soft set called soft expert set [31] that can incorporate the opinions of many experts in one model，which in turn handle the subjectivity that exists in real-life situations in a more practical manner compared to soft set.Among the significant milestones in the development of soft sets and soft expert sets and their generalizations is introducing the single-valued neutrosophic soft expert set(SVNSES)，which combines the advantages of both single-valued neutrosophic set and soft expert.The SVNSES is then improved to the complex neutrosophic soft expert set(CNSES)[32] and complex neutrosophic soft expert relation(CNSER)[33] to solve some complicated real-life problems which contain uncertain，indeterminate，and inconsistent data with two dimensions.

1.1 Novelty

Recently，Al-Sharqi et al.[34]introduced interval-valued complex neutrosophic soft set(I-VCNSS)as a combination of interval complex neutrosophic set and soft set to deal with the problems involved periodicity information and varies with time in interval forms.This model is useful for handling these problems with two-dimensional characterization properties.To make this model more practical for improving new decision-making results，we will improve it into interval-valued complex neutrosophic soft expert sets(I-VCNSES)by extending interval-valued neutrosophic soft expert set from real space to complex space in order to incorporate the advantages of soft expert sets to the intervalvalued complex neutrosophic soft sets.The novelty of I-VCNSES appears in its ability to provide a succinct，elegant，and comprehensive representation of two-dimensional neutrosophic information(information presented by the amplitude terms and information presented by the phase terms)as well as the adequate parameterization and the opinions of the experts，all in an interval form.In addition，the economic-related activities such as the effects of certain financial factors on the economy of a country where the period of time of the influence as a second variable and the opinion of many experts play a key role in the final decision.In this paper，we will solve the same types of decision-making problems that have been solved by CNSES and CNSER by using the interval-based membership structure while defining the I-VCNSES.I-VCNSES can describe more information range by virtue of the interval membership values，which more accurately express decision makers’evaluation information and cause less information distortion.

1.2 Motivation and Contribution

The main contribution and motivation behind this research can be summarized below:

(1)We extend the concept of I-VNSES that is given in Section 3 to I-VCNSES to incorporate the time frame offered by phase terms，as well as the capacity to express ambiguous，indeterminate，and inconsistent data in two dimensions.

(2)We define some basic operations related to our two notions(I-VNSES and I-VCNSES)，namely the complement，union，intersection，AND，and OR.In addition，prove some related properties.

(3)In terms of the application in Section 5，we propose an algorithm to solve decision-making problems in the economic field by converting our model from the complex state(I-VCNSES)to the real state(I-VNSES)and then providing in detail decision steps.

(4)In some real-life problems which the user cannot be solved by soft expert set，fuzzy soft expert set[35]，intuitionistic fuzzy soft expert set[36]，neutrosophic soft set expert set[37]，intervalvalued generalized fuzzy soft expert set[38]，our first proposed interval neutrosophic soft expert set，etc.To help the user to overcome such problems，an interval-valued complex neutrosophic soft expert set has been introduced.

(5)An interval-valued complex neutrosophic soft expert set(I-VCNSES)can be viewed as follows:soft expert set(SES)⊆fuzzy soft expert set(FSES)⊆intuitionistic fuzzy soft expert set(IFSES)⊆interval-valued generalized fuzzy soft expert set(I-VGFSES)⊆neutrosophic soft expert set(NSES)⊆interval-valued neutrosophic soft expert set(I-VNSES)⊆interval-valued complex neutrosophic soft expert set(I-VCNSES).So，it is more effective and useful.

(6)Finally，the main feature in our concept(I-VCNSES)is the presence of the amplitude and phase and their memberships in the form of intervals，and this gives the user more flexibility in the decision-making process.

1.3 Organization of Paper

Based on the below flowchart，we review how to organize our manuscript briefly.

2 Preliminaries

In this section，we recapitulate the concepts of interval-valued neutrosophic set(I-VNS)，complex neutrosophic sets(CNS)and interval-complex neutrosophic set(I-CNS)and give an overview of the operations structures of these concepts that are relevant to the work in this paper.

Definition 2.1.[12] LetUbe a space of points(objects)with generic elements inUdenoted byu.Then an I-NSAinUis characterized by three membership functions that are a truthTA(u)，indeterminacyIA(u)，and a falsehoodFA(u)，such that for each pointuinUwe haveTA(u)=[inf TA(u)，supTA(u)]，IA(u)= [inf IA(u)，sup IA(u)]，FA(u)= [inf FA(u)，sup FA(u)]⊆ [0，1] and 0-≤TA(u)+IA(u)+FA(u)≤3+foru∈U.

Definition 2.2.[12]LetAandBtwo I-NSs over a universeU.Then，the fundamental operations of I-VNSs define as follows:

(1)The complement of an I-VNSAis denoted byAcand is defined asTAc(u)=FA(u)，inf IAc(u)=1-supIA(u)，supIAc(u)=1-inf IA(u)andFAc(u)=TA(u)for anyu∈U.

(2)A⊆B，iff

inf TA(u)≤inf TB(u)，sup TA(u)≤sup TB(u)，inf IA(u)≥inf IB(u)，sup IA(u)≥sup IB(u)，andinf FA(u)≥inf FB(u)，sup FA(u)≥sup FB(u)for anyu∈U.

(3)The union(intersection)of two INSsAandBis an I-VNS denoted asC=A∪(∩)Band the three membership functions of I-VNSs defined as

TA∪(∩)B(u)=[inf TA∪(∩)B(u)，supTA∪(∩)B(u)]

IA∪(∩)B(u)=[inf IA∪(∩)B(u)，supIA∪(∩)B(u)]

FA∪(∩)B(u)=[inf FA∪(∩)B(u)，supFA∪(∩)B(u)]

where

inf TA∪(∩)B(u)=∨(∧)(inf TA(u)，inf TB(u))，

supTA∪(∩)B(u)=∨(∧)(sup TA(u)，sup TB(u))

inf IA∪(∩)B(u)=∧(∨)(inf IA(u)，inf IB(u))，

sup IA∪(∩)B(u)=∧(∨)(sup IA(u)，sup IB(u))

inf FA∪(∩)B(u)=∧(∨)(inf FA(u)，inf FB(u))，

sup FA∪(∩)B(u)=∧(∨)(sup FA(u)，sup FB(u)).

Definition 2.3.[28] A complex neutrosophic setSdefined on a universe of discourseUis characterized by three memberships that are a truth membershipTS(u)，indeterminacy membershipIS(u)，and a falsehood membershipFS(u)that assign a complex-valued grade of membership inSto any elementu∈U.By definition，all values ofTS(u)，IS(u)andFS(u)lie within the unit circle in the complex plane and are expressed byTS(u)=tS(u).ejμS(u)，IS(u)=iS(u).ejωS(u)andFS(u)=fS(u).ejφS(u)wheretS(u)，iS(u)，fS(u)andμS(u)，ωS(u)，φS(u)are both real-valued such thattS(u)，iS(u)，fS(u)belong to the interval[0，1]andμS(u)，ωS(u)，φS(u)belong to(0，2π] and.

Definition 2.4.[29] LetUbe a space of points(objects)with generic elements inUdenoted byu.Then an interval-valued complex neutrosophic set(in short I-VCNS)NinUis defined by three interval membership functions that are a truth interval membership functionTN(u)，indeterminacy interval membership functionIN(u)，and a falsehood interval membership functionFN(u)as a follows:

The phase term’s union(intersection)is defined in the same way as the amplitude term’s union(intersection).The two symbols ∨，∧indicate operators of max and min operators，respectively.

3 Interval Valued Neutrosophic Soft Expert Set

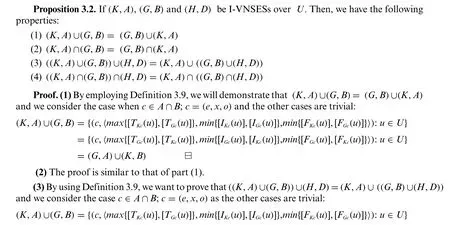
4 Interval-Valued Complex Neutrosophic Soft Expert Sets

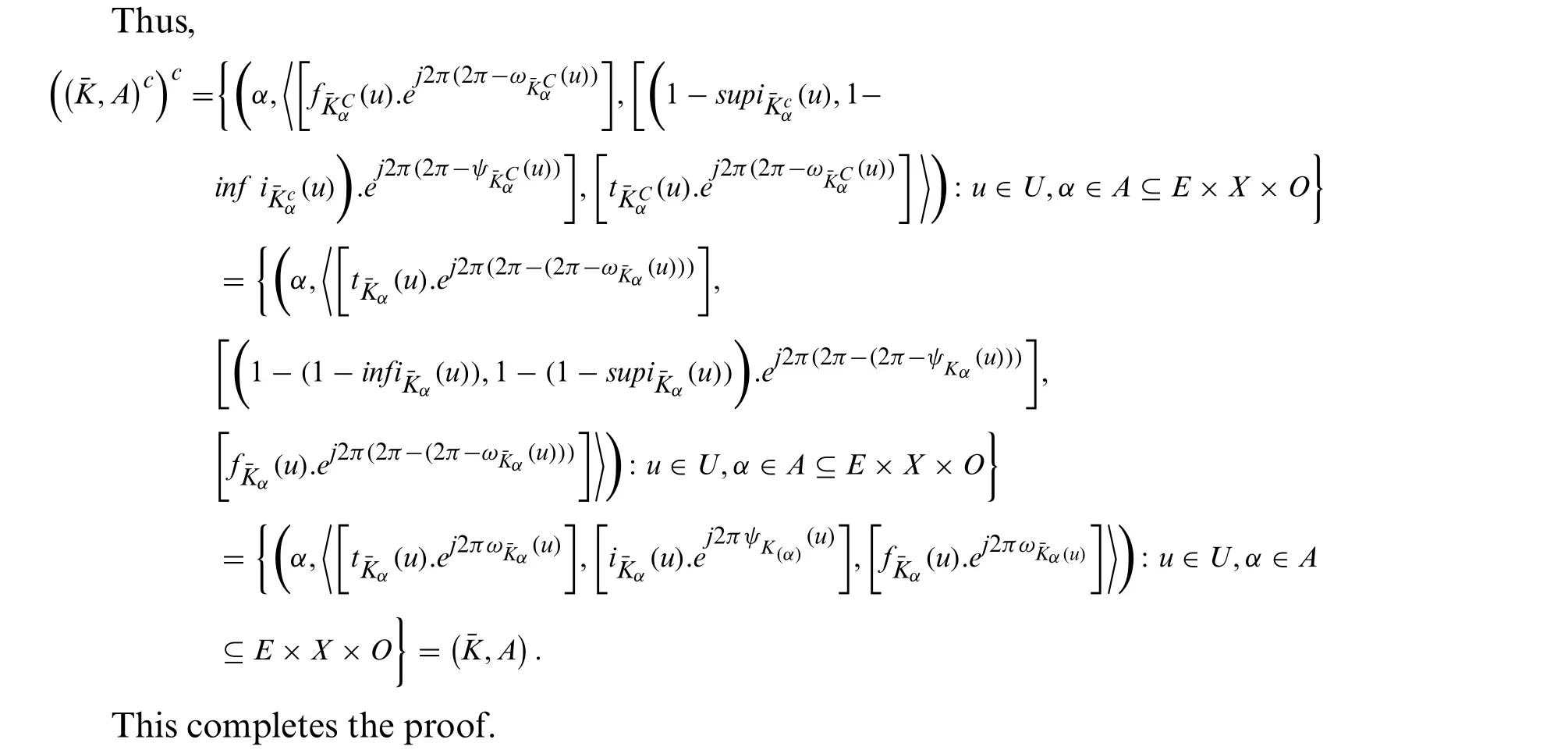
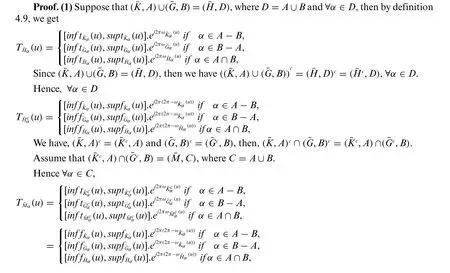
5 Decision-Making on I-VCNSES Environment

In this part，we will highlight the importance of our model in real life by solving one of the decisionmaking problems in the economic field.

Example 5.1.In this example，assume that we are interested in knowing the extent to which the Malaysian economy in 2020 is affected by the four economic factors.The four factors are as follows，the plunge in oil prices and commodities commercial，the slowdown in china’s economy，the tax(GST)on services and goods that applied this year，and exchange rate variability in this year.Our problem is to order these four destinations in descending order from a maximum influencing the Malaysian economy to a minimum affecting the Malaysian economy in 2020.So letU= {u1，u2，u3，u4}，whereu1=plunge in oil prices and commodities commercial，u2=slowdown in China’s economy，u3=tax(GST)on services and goods，u4= exchange rate variability in this year.AndE= {e1，e2，e3} be the set of the parameters that represents the main sectors of the Malaysian economy，wheree1=industry sector，e2= external trade sector，e3= touris msector.We also assume the setX= {p，q}be a set of economic experts which are assigned to analyze those four factors by determining the grade and the full time of the effect of these factors on the aforementioned sectors of the Malaysian-economy as in the following I-VCNSES:

In this situation，the amplitude interval terms measurement the impact degree of the abovementioned factors on the Malaysian economy in 2020，whilst the phase interval terms represent the period of this impact.By this way，the interval-valued complex neutrosophic number

Then，we proceed with SVNSE-values to make the final decision using the SVNSE-method[25].The following steps clarify the proposed algorithm:

Algorithm Step 1.Constructing the I-VCNSES(¯K，A).Step 2.Convert I-VCNSES(¯K，A) to I-VNSES(K，A)by obtaining the values of the weighted aggregation of TK(α)(u)，IK(α)(u)and FK(α)(u)，∀α ∈A and ∀u ∈U as the following formulas:TKα(u)=images/BZ_279_465_862_490_907.pngw1tL¯Kα(u)+w2images/BZ_279_780_862_811_907.png1 2πimages/BZ_279_876_862_907_907.png2πωL¯Kα(u)，w1tU¯Kα(u)+w2images/BZ_279_1453_862_1484_907.png1 2πimages/BZ_279_1549_862_1580_907.png2πωU¯Kα(u)images/BZ_279_1791_862_1816_907.pngIKα(u)=images/BZ_279_453_986_477_1032.pngw1iL¯Kα(u)+w2images/BZ_279_765_986_796_1032.png1 2πimages/BZ_279_861_986_892_1032.png2πψL¯Kα(u)，w1iU¯Kα(u)+w2images/BZ_279_1442_986_1473_1032.png1 2πimages/BZ_279_1538_986_1569_1032.png2πψU¯Kα(u)images/BZ_279_1785_986_1810_1032.pngFKα(u)=images/BZ_279_463_1111_488_1157.pngw1f L¯Kα(u)+w2images/BZ_279_785_1111_816_1157.png1 2πimages/BZ_279_880_1111_911_1157.png2πΦL¯Kα(u)，w1f U¯Kα(u)+w2images/BZ_279_1486_1111_1516_1157.png1 2πimages/BZ_279_1581_1111_1612_1157.png2πΦU¯Kα(u).images/BZ_279_1844_1111_1869_1157.pngwhere the amplitude terms are tL ¯Kα(u)，tU ¯Kα(u)，iL ¯Kα(u)，iU ¯Kα(u)，f L¯Kα(u)，f U¯Kα(u)and the phase terms are ωL ¯Kα(u)，ωU ¯Kα(u)，ψL¯Kα(u)，ψU¯Kα(u)，ΦL ¯Kα(u)，ΦU ¯Kα(u)in the I-VCNSES(¯K，A)，respectively. TKα(u)，IKα(u)and FKα(u) are three interval membership functions in I-VNSES(K，A)，and w1，w2 the weight values for the terms of the amplitude and phase terms，respectively，where w1，w2 ∈[0，1] and w1+w2 =1.Step 3.By taking the arithmetic average of TKα(u)，IKα(u) and FKα(u)，we convert I-VNSES(K，A)to SVNSES(V，A).Step 4.Find the values of MVα(u) = TVα(u)+(1-IVα(u))+(1-FVα(u))3 ，∀u ∈U and ∀α ∈A.Note that MVα(u)is the normalized values of SVα(u) = TVα(u) - IVα(u) - FVα(u)，∀u ∈U and ∀α ∈A.We normalize the elements of S = {SVα(u)，∀u ∈U and ∀α ∈A}，since they represent the degree of influence，where the truth membership function TV(u)，indeterminacy membership function IV(u)，and a falsehood membership function FV(u)are single-valued neutrosophic soft expert functions.Step 5.For both agree-SVNSES and disagree-SVNSES values，take the greatest numerical degree.Step 6.Compute the score of all element ui ∈U by taking the aggregate of the numerical grade of all elements for the agree-SVNSES and disagree-SVNSES，denoted by Pi and Qi，respectively.Step 7.We get the values of the score ri =Pi-Qi for each element ui ∈U.Step 8.Choose the value of the highest score in Z =max ui∈U {ri}.

The decision is to choose valueuias the solution to the problem.If there is more than one value with the highestriscore，then any one of those values can be chosen as the best solution.

Here，we would like to point out that this method(algorithm)is used with decision-making problems that have information that has a known weight(complete weight information).To implement these steps that were mentioned in the algorithm above，we assume that the weight vector to the amplitude terms isw1=0.6.and the weight vector to the phase terms isw2=0.4.

Now，to convert the I-VCNSES(¯K，A)to the I-VNSES(K，A)，and to obtain the weighted aggregation values ofTKα(u)，IKα(u)andFKα(u)，

Hence forα=(e1，p，1)and u = u1the I-VNSES(TKα(u)，IKα(u)，FKα(u))=([0.8，0.96]，[0.09，0.22]，[0，0.06])Then，we apply Step 3 in the algorithm to get(0.88，0.15，0.03)as these values represent SVNESs.In the same method we calculate the other values.Finally，we get Table 1 which includes the values ofMVα(u)in addition to a value of SVNSESs.

Table 1:Values of(V，A)and

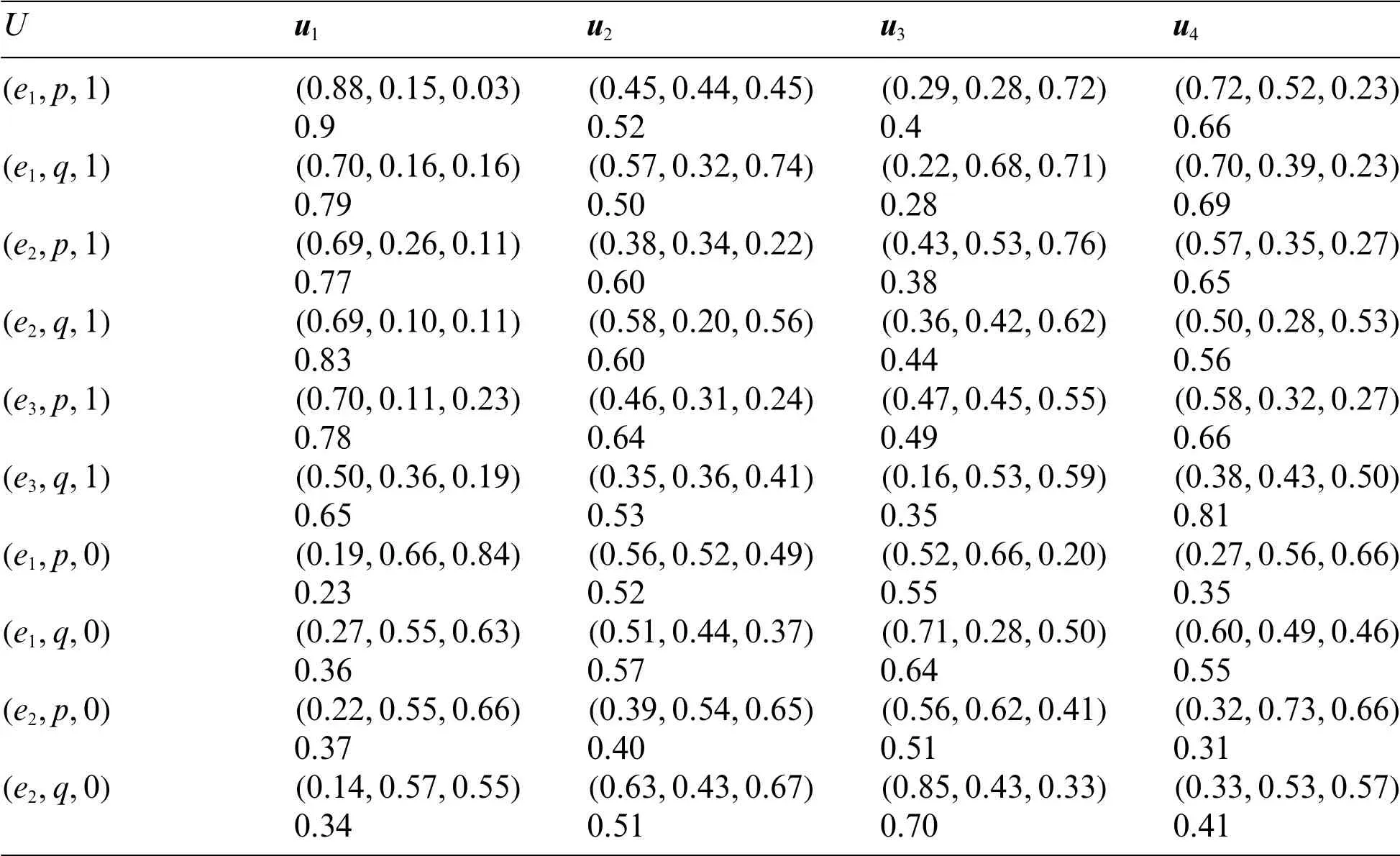
Table 1:Values of(V，A)and

Uu1 u2 u3 u4(e1，p，1)(0.88，0.15，0.03)(0.45，0.44，0.45)(0.29，0.28，0.72)(0.72，0.52，0.23)0.9 0.52 0.4 0.66(e1，q，1)(0.70，0.16，0.16)(0.57，0.32，0.74)(0.22，0.68，0.71)(0.70，0.39，0.23)0.79 0.50 0.28 0.69(e2，p，1)(0.69，0.26，0.11)(0.38，0.34，0.22)(0.43，0.53，0.76)(0.57，0.35，0.27)0.77 0.60 0.38 0.65(e2，q，1)(0.69，0.10，0.11)(0.58，0.20，0.56)(0.36，0.42，0.62)(0.50，0.28，0.53)0.83 0.60 0.44 0.56(e3，p，1)(0.70，0.11，0.23)(0.46，0.31，0.24)(0.47，0.45，0.55)(0.58，0.32，0.27)0.78 0.64 0.49 0.66(e3，q，1)(0.50，0.36，0.19)(0.35，0.36，0.41)(0.16，0.53，0.59)(0.38，0.43，0.50)0.65 0.53 0.35 0.81(e1，p，0)(0.19，0.66，0.84)(0.56，0.52，0.49)(0.52，0.66，0.20)(0.27，0.56，0.66)0.23 0.52 0.55 0.35(e1，q，0)(0.27，0.55，0.63)(0.51，0.44，0.37)(0.71，0.28，0.50)(0.60，0.49，0.46)0.36 0.57 0.64 0.55(e2，p，0)(0.22，0.55，0.66)(0.39，0.54，0.65)(0.56，0.62，0.41)(0.32，0.73，0.66)0.37 0.40 0.51 0.31(e2，q，0)(0.14，0.57，0.55)(0.63，0.43，0.67)(0.85，0.43，0.33)(0.33，0.53，0.57)0.34 0.51 0.70 0.41

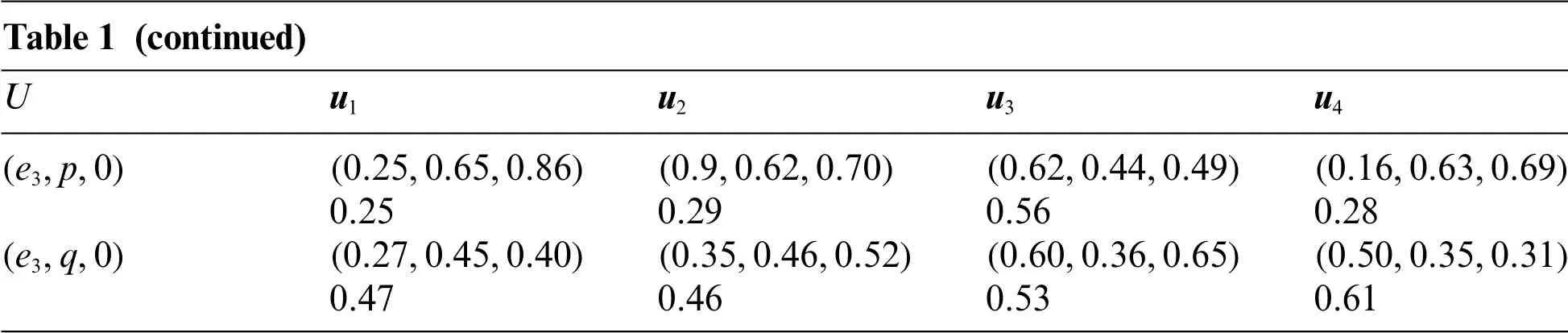
Table 1(continued)Uu1 u2 u3 u4(e3，p，0)(0.25，0.65，0.86)(0.9，0.62，0.70)(0.62，0.44，0.49)(0.16，0.63，0.69)0.25 0.29 0.56 0.28(e3，q，0)(0.27，0.45，0.40)(0.35，0.46，0.52)(0.60，0.36，0.65)(0.50，0.35，0.31)0.47 0.46 0.53 0.61

By Tables 2 and 3，we get the highest numerical grade for the elements in the agree-SVNSES and disagree-SVNSES，respectively.The values ofPi，Qiandriare given in Table 4，whereri=Pi-Qi，represent the final score of each alternative，for alli=1，2，3，4.

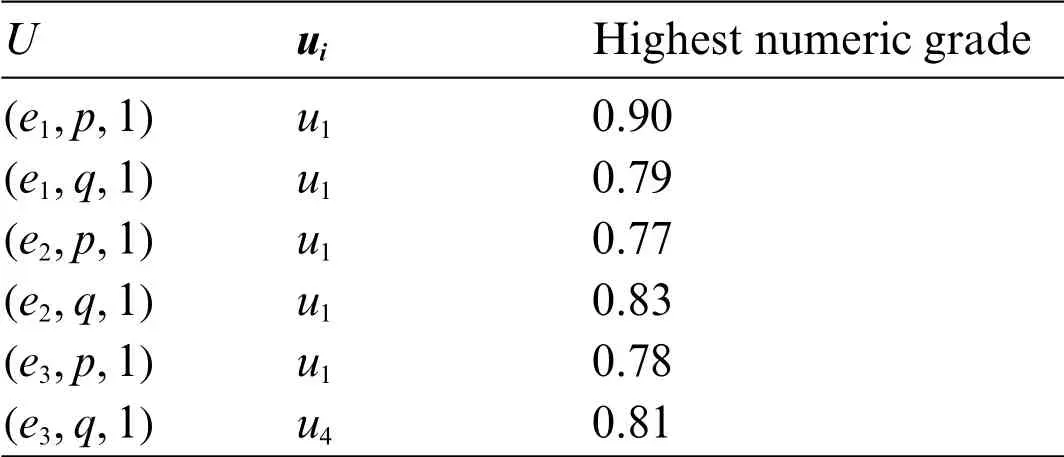
Table 2:Numerical grade for agree-SVNSES

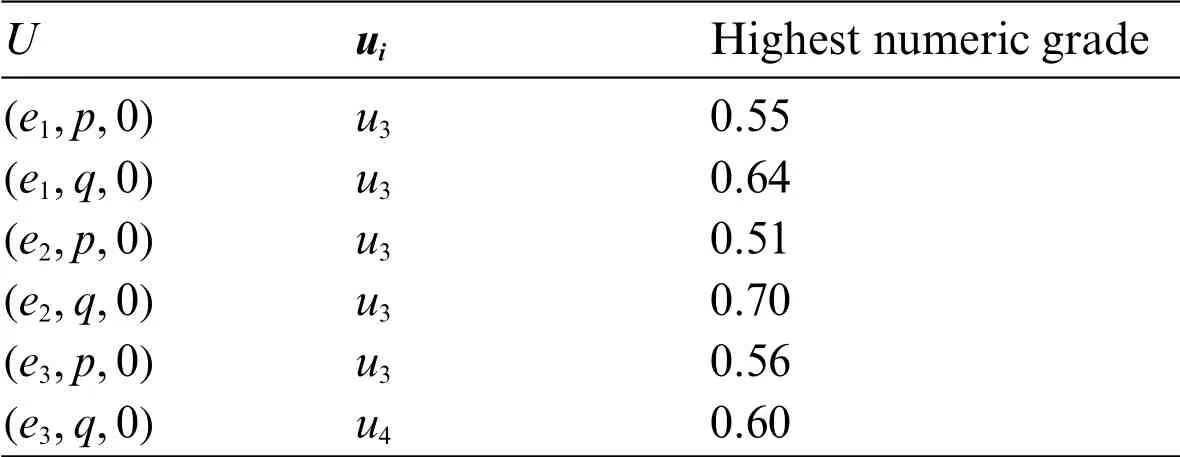
Table 3:Numerical grade for disagree-SVNSES

Table 4:The score ri =Pi -Qi

Finally，according to the Step 8 of proposed algorithm，the maximumriisr1，followed byr4andr2，wherer3is the minimumri.Thus，u1which represents the plunge in oil prices and commodities commercial is the most significant factor influencing Malaysia’s economy in 2020，followed by in influenceu4exchange rate variability in this year andu2the slowdown in china’s economy，whereu3which represents the tax(GST)on services and goods that applied this year is the least influential element in the Malaysian economy in 2020.

6 Comparison between I-VCNSES and Other Existing Methods

In this section，we will now compare our second concept(I-VCNSES)，which is an expansion of our first concept(I-VNSES)with three existing methods，which is neutrosophic soft set(NSS)[39]，single-valued neutrosophic soft expert set(SVNSES)[40]，and complex neutrosophic soft expert set(CNSES).

Because neutrosophic soft set lacks the phase term that indicates the time frame，so it is clear that it is unable to solve the decision-making problem given in this work(see Example 5.1)，which involves two-dimensional data，i.e.，the degree of the influence and the total time of the influence.Another reason is its incapacity to deal with several experts.However，the single-valued neutrosophic soft expert set can deal with more than one expert.But it is not able to deal with problems that involve twodimensional information(amplitude terms and phase terms)like the problem presented in this work.

The complex neutrosophic soft expert set can overcome the problems which the above two concepts cannot overcome by using neutrosophic expert soft set，by virtue of the phase terms which have the ability to represent the time frame of the interaction between the variables as well as parameterization and the opinions of the experts，all in a single set.In comparison，the main distinguishing feature of our proposed is its ability to describe the grade of three complex memberships in the form of an interval that is a subset of the unit interval.Furthermore，since it is difficult for an expert to express his/her certainty by an exact real number，so it is suitable to choose an interval that expresses the certainty level.Therefore，the I-VCNSESs help in modeling the uncertainty and the consequences of any ignorance，mistakes，and confusion of experts.Therefore，it can be judged that our concept is more important and useful than the above-mentioned concepts.

6.1 Advantages and Limitations

Our proposed model has certain advantages and limitations.Firstly，our model(I-VCNSES)has the ability to provide a succinct，elegant，and comprehensive representation of two-dimensional interval neutrosophic information(amplitude terms and phase terms)as well as adequate parameterization and opinions of the experts，all in the form of an interval.Secondly，I-VCNSES includes evaluation information missing in the neutrosophic soft model and single-valued neutrosophic soft expert model，such as the time frame which is presented by the phase term.In addition，it has the added advantage of allowing the users to know the opinion of all the experts in an interval model without the necessity for any additional cumbersome operations.Thirdly，the I-VCNSES that is used in our method has the ability to handle the uncertainty information that is captured by the amplitude terms and phase terms of the complex numbers simultaneously.Fourthly，a new practical formula is employed to convert the interval-valued complex neutrosophic soft expert from the complex state to the real state，which gives decision-making with a simple computational process without the need to carry out directed operations on complex numbers.Fifthly，our model represents the information of two-dimensional in interval form，namely information of amplitude term and phase term，thus making our model more appropriate for use in real-life problems like decision-making，medical diagnosis to select the best alternative.Finally，the interval form which characterized our concept gives the user more flexibility in the real decision-making process，where the real decision we get through our concept is characterized as more trustworthy and more acceptable than the other existing concepts in which there is no attention to the interval form.Therefore，these features mentioned above are essential points that distinguish our model from existing models.Our idea，on the other hand，is incapable of handling discontinuous attribute-value sets that correspond to different attributes.Therefore，we recommend for future studies that this gap be overcome by generalizing our concept to an interval-valued complex neutrosophic hypersoft expert set.

7 Conclusion

A novel mathematical tool is created to highlight the information using time factors and to realize the opinions of all the experts in an interval model.In this article，we established the concept of IV-CNSES by extending our concept of IV-NSES from real space to complex space.The basic operations on both I-VNSES and I-VCNSES，namely subset，complement，union，intersection，AND and OR operations were defined.Subsequently，some basic algebraic properties of these operations were proven.In addition，we showed the importance of this concept in real life through a proposed new algorithm and we applied it to both models to solve a hypothetical decision-making problem related to the economic factors that affected the Malaysian economy in 2020.A comparison of our proposed model with three other existing models indicates the efficiency of our model and also it showed the superiority of our concept over these concepts with flexibility and accuracy in representing twodimensional interval neutrosophic information.Finally，these flexible new extensions are not applied yet in many fields like computer science，social science，medical science，engineering，etc.So，in future work，we plan to combine this concept with other types of algebraic structures such as group[41，42]and ring [43，44].We are wishful to provide our work to other MCDM models and applications for modeling vagueness and uncertainty.

Acknowledgement:We are indebted to Universiti Kebangsaan Malaysia for providing financial support and facilities for this research under the Grant TAP-K005825.

Funding Statement:Universiti Kebangsaan Malaysia Research Grant TAP-K005825.

Conflicts of Interest:The authors declare that they have no conflicts of interest to report regarding the present study.