Seed-Oriented Local Community Detection Based on Influence Spreading

Shenglong Wang，Jing Yang，Xiaoyu Ding，Jianpei Zhang and Meng Zhao

1College of Computer Science and Technology，Harbin Engineering University，Harbin，150001，China

2College of Computer Science and Technology，Chongqing University of Posts and Telecommunications，Chongqing，400065，China

ABSTRACT In recent years，local community detection algorithms have developed rapidly because of their nearly linear computing time and the convenience of obtaining the local information of real-world networks.However，there are still some issues that need to be further studied.First，there is no local community detection algorithm dedicated to detecting a seed-oriented local community，that is，the local community with the seed as the core.The second and third issues are that the quality of local communities detected by the previous local community detection algorithms are largely dependent on the position of the seed and predefined parameters，respectively.To solve the existing problems，we propose a seed-oriented local community detection algorithm，named SOLCD，that is based on influence spreading.First，we propose a novel measure of node influence named k-core centrality that is based on the k-core value of adjacent nodes.Second，we obtain the seed-oriented local community，which is composed of the may-members and the must-member chain of the seed，by detecting the influence scope of the seed.The may-members and the must-members of the seed are determined by judging the influence relationship between the node and the seed.Five state-of-art algorithms are compared to SOLCD on six real-world networks and three groups of artificial networks.The experimental results show that SOLCD can achieve a high-quality seed-oriented local community for various real-world networks and artificial networks with different parameters.In addition，when taking nodes with different influence as seeds，SOLCD can stably obtain high-quality seed-oriented local communities.

KEYWORDS Complex network;local community detection;influence spreading;seed-oriented;degree centrality; k-core centrality;local expansion

1 Introduction

In recent years，complex networks have been prevalent in various domains，such as social media，bioengineering，computer networks and e-commerce shopping [1].An important property of complex networks is the community structure，which can be defined as a group in which entities are tightly connected [2].Community structures，in which the entities are represented by the nodes and the relationship between entities are represented by the links，widely exist in the real world [3].In addition，nodes within the same community are more similar than those between different communities.In other words，a community is in some fashion separated from the other communities [4].

Research on community detection has attracted extensive attention in the last two decades.As an important branch of community detection，local community detection has rapidly developed because of its nearly linear computing time and the convenience of obtaining the local information of real-world networks.Most of the existing local community detection algorithms concentrate on detecting the community with the optimal quality function where a seed is located [5-9].The community with the optimal quality function is the closest to the community in the real world，and its core members are also the closest to the core members of the real-world community but not necessarily the given nodes.It is also of practical significance to obtain the local members that can be influenced by an individual in the community.Sometimes，we just want to know who has the ability to influence the network，not which community this person is located.In addition，this person may not be important in the community，but there may be others who will be affected by him.Therefore，this paper proposes an algorithm aimed at detecting the local community with the seed as the core for the first time.

Many excellent local community detection algorithms have been proposed.However，some problems still hinder the development of local community detection algorithms.First，as mentioned above，the communities detected by previous local community detection algorithms do not take the seed as the core.This leads to the seed deviation problem.Second，the quality of the detected communities depends on the location of the seed.This leads to the seed dependence problem.Third，the quality of the detected communities depends on the predefined parameter.This leads to the parameter dependence problem.In addition，the predefined parameter makes it difficult and time-consuming to obtain the most reasonable parameter.

This paper proposes a seed-oriented local community detection algorithm，namedSOLCD，based on influence spreading to solve the three problems mentioned above.In order to solve the seed deviation problem and the seed dependence problem，SOLCDexpands the community by constantly exploring the influence scope of the seed so the seed is always in the influence center of the detected community.This ensures that the seed is in the core position in the resulting community and the quality of the resulting community.In order to measure the node influence，we proposek-corecentrality based on thek-coredecomposition algorithm [10].In order to solve the parameter dependence problem，SOLCDuses the influence spreading method that needs no parameter.In order to verify the quality of the resulting community，we propose a local community effectiveness index(LCE)and a local community uniqueness index(LCU)to evaluate the quality of the seed-oriented local community.The main contributions of this paper can be summarized as follows:

· We propose a seed-oriented local community detection algorithm for the first time，namedSOLCD，based on influence spreading.SOLCDhas the capacity to detect the local communities with seeds as the core，which not only enables people to obtain the seed-oriented local communities，but also makes obtaining the information of the target node more quickly and effectively.

· We propose a new measure of node influence，namedk-corecentrality，based on thek-coredecomposition algorithm.Empirical evaluations on artificial and real-world networks show that the proposed algorithm based onk-corecentrality is robust and efficient in detecting seed-oriented local communities.

· We propose two indices that can effectively evaluate the quality of seed-oriented communities:a local community effectiveness index(LCE)and a local community uniqueness(LCU)index.

· The experimental results on both artificial and real-world networks show that theSOLCDhas the capacity to detect high quality seed-oriented local communities with stronger robustness than some of the latest algorithms.In addition，SOLCDcan effectively solve the three problems existing in the research of local community detection:the seed deviation，the seed dependence and the parameter dependence problem.

The rest of this paper is organized as follows.Section 2 reviews the related works on local community detection.In Section 3，we describe the proposed algorithm in detail，and introduce a new node influence measure based onk-corecentrality.In Section 4，we introduce a local community effectiveness index and a local community uniqueness index to estimate the quality of the detected local communities，then we test the proposed algorithm and compare it with some latest algorithms.Section 5 summarizes our work.

2 Related Works

Most of the existing local community detection algorithms based on the local expansion method consist of two major components:seed selection and community expansion.In the seed selection process，the algorithms select an appropriate node or node set as the seeds to replace the given node so as to be more suitable for community expansion.In the community expansion process，the algorithms expand the community，composed of seeds originally，by running a variety of expansion mechanisms.This section outlines the current research on the local expansion method and describes the dilemma of the current research.

2.1 Seed Selection

Seed selection is widely concerned because of its importance to the local expansion method [11]，and various seed selection methods have been proposed.Lancichinetti et al.[12]randomly selected a node as the seed，which makes the results of this algorithm uncertain and leads to a weakness of this algorithm.Similarly，Baumes et al.[13] proposed an algorithm randomly selects edge as the seed.However，in the searching seeds process，this algorithm produces multiple duplicate communities，which consumes considerable time.Lee et al.[14] took a set of k nodes，in which each pair of nodes had an edge，namely，k-clique，as the seeds.Whang et al.[15]proposed a new seed selection strategy based on the personalPageRankclustering scheme.The key to this algorithm is neighborhood inflation，in which seeds are modified to represent their entire node neighborhood.Ding et al.[16] proposed a robust two-stage local community detection algorithm(RTLCD)to detect the core member of the real-world community as a substitute for the given node based on the node relation strength.Cheng et al.[17] scored the nodes in a network using the technique for order of preference by similarity to ideal solution(TOPSIS)and took the node with the highest score as the seed.In order to reduce the impact of the seed dependence problem，Guo et al.[18] take the core area which is detected by adding neighboring nodes with the maximum optimizedlocal modularity density，as the seeds.Ni et al.[19] took the nodes whose fuzzy relationship with theirNGCnodes was greater than the threshold as the seeds.AnNGCnode [20] is the nearest node with greater centrality.

These excellent seed selection methods mentioned above can effectively improve the quality of the detected community，but there are still two dilemmas that have not received much attention.First，some seed selection methods，such as the random seed selection method，directly take the given node as the seed [12-15，21].This leads to the quality of the detected community depending heavily on the location of the seed，which greatly affects the accuracy of the community detection algorithm.Second，some seed selection methods，such asRTLCD，TOPSIS[16，17，19，20]，select the nodes that are more suitable for community expansion as substitutes for the given node，which effectively alleviates the dependence of the algorithm on seed location.However，the replacement of the given node by the seed selection method will cause the given node to deviate from the result community，which makes the existing local community detection algorithms unable to effectively detect the community dominated by the given node.

2.2 Community Expansion

The function of community expansion is to expand the initial community into a local community by adding adjacent nodes to the detected community.Common community expansion methods include the quality function [5-9] and the influence spreading [22-26].

The quality function defines the community structure in a network，which can be used to evaluate the community division quality [27].Yang et al.[28] studied 13 quality functions and tested their sensitivity，robustness and performance on 230 large real-world networks.Based on this research，Yang et al.[28] classify quality functions into four categories:(1)links within a community，(2)links outside a community，(3)links within and outside a community，and(4)modularity.

The main idea of the influence spreading method is to score each node with an influence evaluation mechanism and spread it to the entire network.Raghavan et al.[29] proposed the label propagation algorithm(LPA)based on the epidemic spreading model.LPAassigns each node in the network a unique label，and then updates the node label to be consistent with the label of its majority neighbors until the label no longer changes.Because of the convenience and efficiency ofLPA，researchers have successively proposed a series of algorithms based onLPA.Xu et al.[30] proposed an improvedLPAalgorithm based on a two-level neighborhood similarity measure namedTNS，which could help to further divide a network into communities accurately.Inspired byLPA，Wu et al.[31] merged communities whose size was smaller than a threshold，where the threshold was based on a reasonable communities’scale，into reasonable communities to increase the community division accuracy.Based onLPA，Gregory et al.[32] proposed a method with the ability to detect overlapping communities，namedCOPRA(community overlap propagation algorithm).Tang et al.[33] revealed the overlapping nodes and proposed an algorithm based on thek-lowest-influence.

The community expansion methods described above can obtain high-quality local communities，but there are still some problems that need to be addressed vigorously.First，some community expansion methods need to set parameters before their execution [34，35]，which make methods difficult and time-consuming to obtain the most reasonable parameter.Second，existing expansion methods are dedicated to expanding the seed to a community which is the most similar to the real-world community.However，in the community expansion process，the given node may be at the edge of the community，or even be removed from the community.That is，there are no expansion methods that focus on the local community with seeds as the core.

3 Motivations and Basic Definitions

3.1 Motivation

As discussed in Section 2，local community detection algorithms have made excellent achievements in terms of the local expansion method，but there are still three problems hindering the development of community detection research:the seed deviation problem，the seed dependence problem and the parameter dependence problem.

The motivation of solving the three problems is as follows.In order to solve the seed deviation problem and the seed dependence problem，we propose a seed-oriented algorithm，which will always take the given node as the seed，and always take the seed as the influence core in the process of community expansion.In order to solve the parameter dependence problem，we propose a local community detection algorithm based on influence spreading without any parameters.

3.1.1 Motivation for Seed-Oriented Local Community

Traditional local community detection algorithms aim to expand from the seed node to the community that is the most similar to the real community.We call these algorithms community quality-oriented local community detection algorithms.However，in the real world，every individual should have the opportunity to build its own local community that takes the individual as the center.For example，different departments with students can be considered as different communities from the perspective of a college.Every student should have the opportunity to build his own local friendship-community consisting of the members from multiple departments.In addition，every student should have the opportunity to become the center of his own local friendship-community.In this paper，we call this type of local community a seed-oriented local community.Different from traditional algorithms，this paper proposes a seed-oriented local community detection algorithm aiming to build the seed-oriented local community of a given node.

The research value of detecting seed-oriented local communities is as follows.First，when the goal is to measure the influence of a person on the other individuals，we only need to detect the seed-oriented local community where this person is located rather than the quality local community，which helps to improve the efficiency of an algorithm.Second，even if an individual is marginalized in a quality oriented community，this individual influences other individuals in a seed-oriented community.In contrast，in a seed-oriented community，the influence of this individual on the other individuals may be greater than that of the core members of a quality oriented community.Third，as a marginal individual in a quality oriented community，the local influence in a seed-oriented community may be greater than that of the core members in the quality-oriented community.

In a community，core members are described as members at the center of the community，hub members are members in close contact with members outside the community，and outlier members are members on the boundary of the community.In fact，core members have higher influence than hub members，and hub members have higher influence than outlier members.Based on this fact，this paper proposes a seed-oriented local community detection algorithm based on influence spreading.The proposed algorithm is guided by the following:a node tends to become a member of the community that is generated by an adjacent node with higher influence.

A sample of the seed-oriented local community detected by the proposed algorithm is shown in Fig.1.We show a seed-oriented local communityCand its neighboring subnetworkN.The figure shows that all the may-members ofChave an influence not lower than that of the seed node.In addition，all the must-members ofC，which are connected with the seed node using must-member chains，have an influence lower than the seed node.

Figure 1:A sample of seed-oriented local community detected by the proposed algorithm. C denotes the seed-oriented local community，N denotes the neighbor sub-network of C.The nodes colored yellow are the must-members of C，the nodes colored blue are the may-members of C，the node colored red is the seed node.The number inside the node is the node influence.Solid lines connect the nodes within C，dotted lines connect the nodes between C and N

3.2 Problem Definition

3.3 Basic Definitions

In this paper，we detect the seed-oriented local communities by detecting the influence scope of the seed in a network.To facilitate readers following along with this paper，we display the research path of this paper in Fig.2，and the subsection will provide the related definitions of this paper.

Figure 2:The research path of this paper

Definition 1(Node neighbors).The node neighbors of node v are defined as follows:where A is the adjacent matrix of graphG，andAuv=1denotes that there is a link between nodevand nodeu.

Definition 2(Natural community).The natural community of node v is defined as follows:

The natural community of nodevis a node set composed of nodevand its neighbors.

Definition 3(Must-member).The must-members of node v are defined as follows:

The must-members of nodevis a node set composed of nodev’s neighbors that have lower node influence than that of nodev.

Definition 4(May-member).The may-members of node v are defined as follows:

The may-members of nodevis a node set composed of nodev’s neighbors that do not have lower node influence than that of nodev.

Property 1(Transitivity of influence relationship between must-members).Suppose nodeBis a must-member of nodeA，and nodeCis a must-member of nodeB.Then，the conclusion we can obtain is that there must be a path from nodeCto nodeA，that is nodeCmust be reachable to nodeA，and nodeAmust have no lower influence than nodeC.

Proof 1.According to theDefinition 3，we can know that nodeAis a neighbor of nodeBand nodeBis a neighbor of nodeC，so there must be a path from nodeAto nodeBto nodeC.In addition，nodeBhas lower node influence than that of nodeAand nodeCowns lower node influence than that of nodeB.Therefore，we can conclude that nodeCmust be reachable for nodeA，and nodeCmust have lower node influence than that of nodeA.

Definition 5(Must-member chain).The must-member chain from nodeAto nodeBis defined as follows:

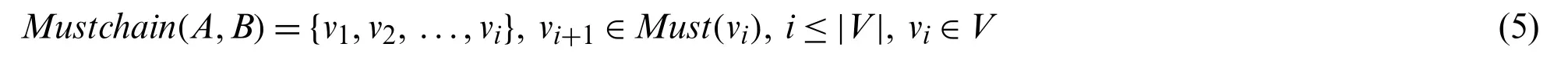
The must-member chain can be regarded as a queue composed of nodes in the network.The members in the queue are arranged in descending order according to their node influence，and each member in the queue must be a must-member of the previous member.

Definition 6(Reachable must-member).A reachable must-member of node v is defined as follows:

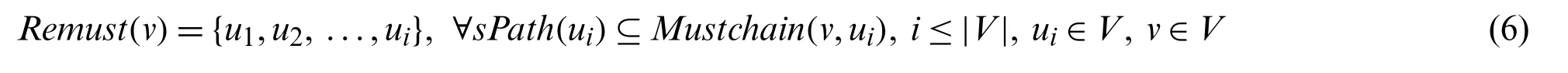
wheresPath(v，ui)denotes the nodes on the shortest path from nodeuto nodev.

A reachable must-member of nodevis a node which is reachable from nodev，and each shortest path from nodevto this node must be a must-member chain.

Definition 7(Seed-oriented local community).The seed-oriented local community of seed node v is defined as follows:

The seed-oriented local community of the seed node is a node set composed of the seed，the may-members and all the reachable must-members of the seed node.

3.4 The Proposed Algorithm

In this subsection，we will show the flowchart of the proposed algorithm in Fig.3，and the pseudocode of the proposed algorithm in Algorithm 1.The proposed algorithm includes two phases:obtaining the may-members phase and obtaining the must-members phase.The processes of each phase are as follows:

Initialization(Line 1).Line 1 initializes listListmayand listListmustto empty to store the may-members and must-members of seed node respectively.Line 1 assigns the seedvseedto the queueQ.

Obtaining may-members(Lines 2-7).Phase 1 aims to obtain the may-members of the seed node.Min line 4 denotes the node influence evaluation mechanism.Line 3 obtains all the neighbors of the seed node.If the influence of the neighborviis higher than that of the seed node(Line 4)，then line 5 assignsvito the may-member listListmay.

Obtaining must-members(Lines 8-26).Phase 2 aims to obtain the must-members of the seed node.When the queueQis not empty(Line 9)，Line 10 removes the first nodevfirstof Q.

Line 11 obtains all the neighbors ofvfirst.If the influence of the neighborviis lower than that ofvfirstandvidoes not belong to the must-member listListmust(Line 12)，then line 16 sets the flag to true(Line 16).The flag is a Boolean variable that is used to determine whether the node is a must-member of the seed node.Line 14 obtains the nodevnfrom the union of the neighbors of the seedvi，Q andListmust.If the influence of the neighborvnis lower than that ofvi(Line 15)，then Line 16 sets the flag to false.Lines 15-16 are to ensure that node vi is the reachable must-member of nodevfirst.If the flag is true，Line 20 assigns nodevitoQ.Line 24 assignsvfirstto the must-member listListmust.Line 25 removesvfirstfromQ，and repeats the algorithm until the queueQis empty.

Figure 3:The flowchart of SOLCD

Finally，the union of the seed，may-member listListmayand must-member listListmustis the seed-oriented local community of the seed nodevseed.

Algorithm 1:The seed-oriented local community detection algorithm(SOLCD)Input:Graph G=＜V，E ＞，link set E，node set V，seed node vseed，Node influence measure Inf.Output:Community C.Process:1:Initialize Listmay=φ，Listmust=φ，Q=vseed 2:Phase 1.Get may-members of vseed 3:for all vi ∈N(vseed) do 4:if Mvi ≥Mvseed then 5:Listmay=Listmay ∪{vi}6:end if 7:end for 8:Phase 2.Get must-members of vseed 9:while Q/=φ do 10:Get the first element vfirst of Q

Algorithm 1:(Continued)11:for all vi ∈N(vfirst) do 12:if Infvi ＜Infvfirst&&vi /∈Listmust then 13:Flag = true.14:for all vn ∈N(vi)∩(Q ∪Listmust) do 15:if Infvn ＜Infvi then 16:Flag = false 17:end if 18:end for 19:if Flag = true then 20:Q=Q ∪{vi}21:end if 22:end if 23:end for 24:Listmust=Listmust ∪{vfirst}25:Q=Q-{vfirst}26:end while 27:return C={vseed ∪Listmay ∪Listmust}

3.5 Time Complexity Analysis

4 Experiments and Analyses

The experimental environment of this paper is as follows:the proposed algorithm and the comparison algorithms are programmed inJAVA;all the programs involved in this paper are running in a computer withIntel(R)Core(TM)i5-4590 CPU，3.3 GHz，16GB RAM.The experiments are implemented in the proposed algorithm and six comparison algorithms on six real-world networks and three groups of different parameters artificial networks，and the experimental results are verified by four commonly used local community indicators and two proposed by this paper seed-oriented community indicators.Table 2 displays related symbols and their explanations.

Table 1:The time complexity of proposed algorithm and comparison algorithms

Table 2:Symbols and descriptions

4.1 Measures of Node Influence

K-corecentrality.This paper proposes a new measure，thek-corecentrality，which is based on thek-coredecomposition algorithm [10]，for node influence.

whereKiis thek-corecentrality of nodei，Niis the neighbors of nodei，andcjis the core value of nodej.

K-core.K-core[1，41] is a subgraph of networkGin which the smallest degree of nodes isk.Ink-coredecomposition algorithms [42-44]，thek-coreis defined as a subgraph of the network where all nodes have a degree not less thank，and a(k+1)-coremust be a subgraph of thek-core.If we say a node has a core valuek，it means that the node belongs to ak-coreso that the node’s core value is the maximum value.In addition，when nodeAhas a higher influence thanB，both of the core values and thek-corecentrality of nodeAare higher than those of nodeB.

4.2 Simple Test of SOLCD

In order to illustrate the proposed algorithm，we make simple tests on the core members，the hub members and the outlier members ofKarate Club Network[45].In the analysis，we use the inner-links to represent the links within a community and the outer-links to represent the links connecting different communities.It is worth noting that the tests do not mean to compare the seed-oriented local communities detected by the proposed algorithm with the real communities in a global sense，but to show the regularities of the distribution of the nodes of seed-oriented local communities.Fig.4 shows the distribution ofKarate Club Network，in which node1and node34represent the administrator and the instructor respectively.

Figure 4:The distribution of karate club network

4.2.1 Tests of the SOLCD on Core Members

From the real network of Karate Club Network，we choose node1and node34which own the greatest number of inner-links as the core members.From Fig.5，we can observe that most of the inner-members of the seed-oriented communities are also the inner-members of the real communities.

Figure 5:Tests of SOLCD on core members.(a)and(b)are the seed-oriented local communities of nodes 1 and 34 generated by SOLCD.Nodes colored yellow are the must-members，nodes colored blue are the may-members and nodes colored red are the seed nodes

4.2.2 Tests of the SOLCD on Hub Members

From the real network of Karate Club Network，we choose node3and node9which have some outer-links as the hub members.From Fig.6，we can see that the seed-oriented local communities generated from hub members prefer to take the core members(nodes1and34)as may-members.This phenomenon is because hub members connect different communities and have lower influence than core members.Besides that the communities generated from hub members have smaller size than the communities generated from core members.

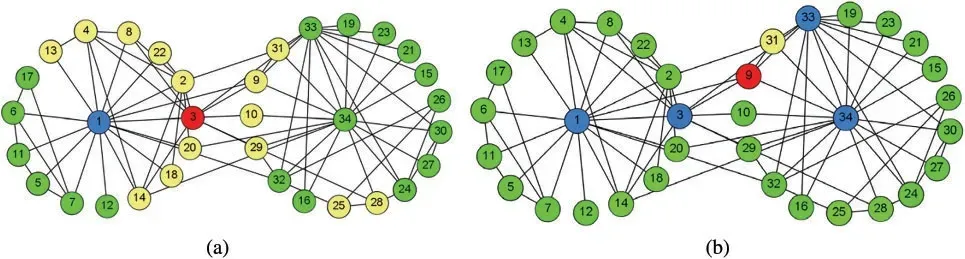
Figure 6:Tests of SOLCD on hub members.(a)and(b)are the seed-oriented local communities of nodes 3 and 9 generated by SOLCD.Nodes colored yellow are the must-members，nodes colored blue are the may-members and nodes colored red are the seed nodes

4.2.3 Tests of the SOLCD on Outlier Members

From the real network of Karate Club Network，we choose node12and node27with a few of inner-links as the outlier members.From Fig.7，we can observe that the seed-oriented local communities generated by the outlier members tend to have more may-members than mustmembers.This is because outlier members are peripheral members of communities and have lower influence value than that of the core members(nodes1and34)and that of the hub members(nodes3and9).

Figure 7:Tests of SOLCD on outlier members.(a)and(b)are the seed-oriented local communities of nodes 12 and 27 generated by SOLCD.Nodes colored yellow are the must-members，nodes colored blue are the may-members and nodes colored red are the seed nodes

4.2.4 Characteristics of SOLCD

According to samples on core members，hub members and outlier members，we could summarize some characteristics ofSOLCDas follows:

·SOLCDis a self-adaptive algorithm without any help of pre-defined parameters.This avoids the parameter-dependent problem.

· Regardless of the seed node’s attributes(core member，hub member or outlier member)，the detected seed-oriented local community always take the seed node as core member.This solves the seed-deviation problem.

4.3 Evaluation Criteria

Two common used community detection algorithm evaluation criteria are adopted in this paper to verify the performance ofSOLCD:the Normalized Mutual Information [46](NMI)and

F-score[47].

4.3.1 Normalized Mutual Information

Danon et al.[46] used information entropy as the measurement of the similarity between realworld communities and the resulting communities，which is named normal mutual information(NMI).The basis ofNMIis a confusion matrixNin which the rows represent the information of real-world communities and columns represent the information of the resulting communities.That is，the intersection of real-world communities and resulting communities are represented by elementNijof matrixN，which denotes the numbers of nodes that exist in both communities.NMI[46] is defined as follows:

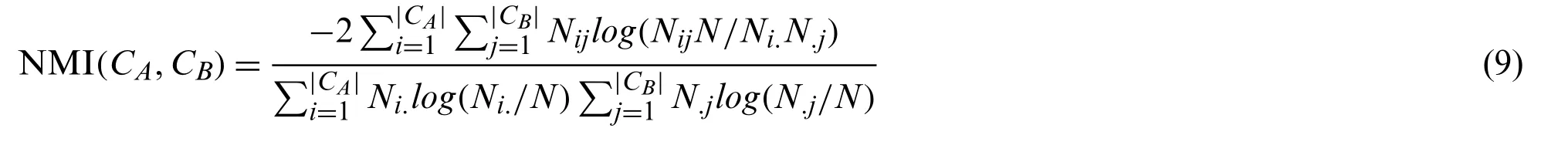
where|CA|represents the number of real-world communities and|CB|represents the number of resulting communities.Ni.andN.jdenote the sums of the elements in Rowiand Columnj，respectively.

NMIis an evaluation index commonly used to assess the community division quality.The better community division quality，the higher the value ofNMI.The maximum value ofNMIis1when the resulting community is the same as the real-world community.

4.3.2 F-Score

F-score[47] is widely used in classification methods to evaluate the quality of the model.The formula ofF-scoreis as follows:

whereCRrepresents the nodes of real-world communities andCDrepresents the nodes of detected communities.

Recallis the ratio of the number of correctly found nodes to the number of nodes in the realworld community.Precisionis the ratio of the number of correctly found nodes to the number of nodes in detected community.F-scoreis the weighted harmonic average ofRecallandPrecision.

4.3.3 LCE

In this paper，we propose a local community effectiveness index(LCE)to measure the quality of seed-oriented local communities.High-quality seed-oriented local communities should satisfy the condition that the seed node is the center of the detected community.In other words，the sum of the shortest path lengths from the seed node to each node of the seed-oriented local community should be smaller than that from other nodes in the rest of the community.LCEis defined as follows:

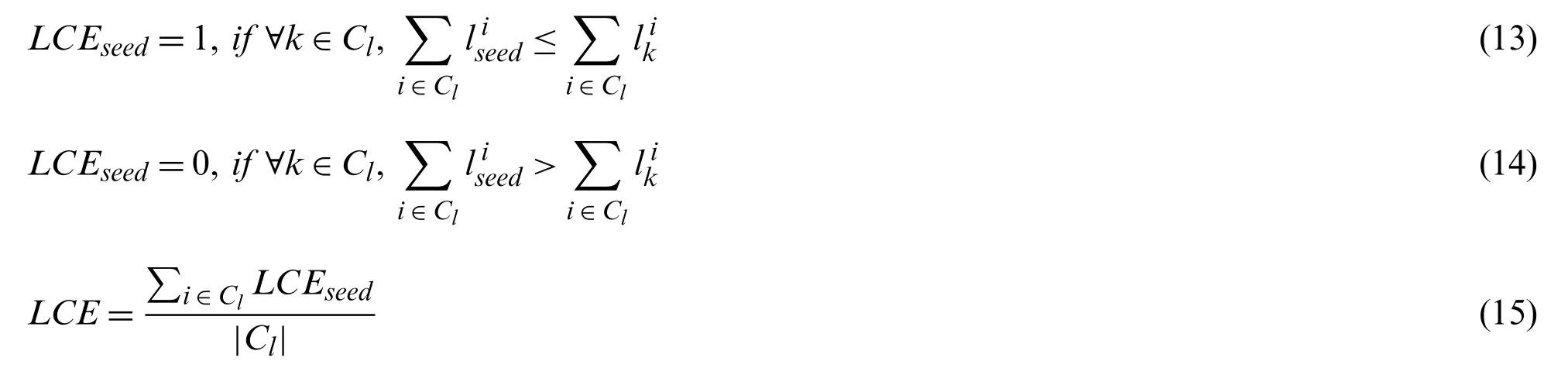
whereLCEseeddenotesLCEvalue of the seed node seed-oriented local community;Cldenotes the detected local community，andl ikdenotes the length of the shortest path from nodekto nodei.We defineLCE=1when the sum of the shortest path lengths from the seed node to the other nodes among all the nodes of the community is the maximum;otherwise，LCEseed=0.

4.3.4 LCU

This paper proposes a local community uniqueness index(LCU)to estimate the uniqueness of seed-oriented local communities.A high quality seed-oriented local community should satisfy the condition of having a unique distribution of nodes.LCUis defined as follows:

where |Cdistintct|denotes the number of distinct valid local communities，and |Cvalid|denotes the number of all valid local communities.

4.4 Datasets

4.4.1 Artificial Networks

This paper used Lancichinetti et al.[48](LFR)benchmark networks to generate various types of artificial networks to evaluate the performance of the proposed algorithm.TheLFRbenchmark network is widely used in the research of complex networks to generate artificial networks that have the same properties as real-world networks.The significance of the parameters affecting the properties of the generated artificial network is as follows.The mixing parameterμdetermines the difficulty of detecting the communities for the algorithm.The higher the value ofμis，the harder it is to detect the community structure.anddetermine the maximum and minimum size of the communities within the artificial network，respectively;¯d determines the mean degree of the nodes within the network anddmaxdetermines the maximum degree of the nodes within the network;and On and Om determine the overlapping degree of communities in the network.On denotes the number of overlapping nodes between communities and Om denotes the number of overlapping communities of overlapping nodes.

In order to generate different types of artificial networks，we set the parameters of theLFRbenchmark network as displayed in Table 3，where the expression [a:b:c] represents the value of parameter value ranges from a tocwithaspanning ofb.As shown in Table 3，we generate artificial networks in three groups of parameters:LFR-μ，LFR-αsizeandLFR-αdegree.These three parameters are used to test the performance of the proposed algorithm in community structure identification，community diversity and node diversity.In order to avoid the influence of the randomness of the generated artificial networks，we generate 10 artificial networks for each parameter and take the average value as the experimental results.

Table 3:The parameter configuration for LFR benchmark network

4.4.2 Real-World Networks

This paper used6real-world networks to test the performance of the proposed algorithm.The characteristics of the real-world networks are listed in Table 4.By observing the relationship between34members of a karate club at an American university，Zachary et al.proposed thekarate club network[45] in which nodes represent the members of the club and the links between nodes represent the relationships between nodes.By observing the habits of 62 bottlenose dolphins living in New Zealand，Lusseau et al.[49] found that the communication of these dolphins showed a specific pattern and proposed thedolphin network，in which each node represents a bottlenose dolphin and the link between two dolphins represents that these two dolphins are in frequent contact.Thebooks networkis a network of the purchasing records of political books on Amazon [50].In the network，the nodes represent political books and a link between two books indicates that they are purchased together frequently.Thefootball networkis the records among the college teams that participated in the 2000 American football season [51].In the network，each node represents a participating university and a link means that there was a match between two colleges.TheAmazon networkis a network of purchasing records on Amazon [28].TheDBLPnetwork is a network of a scientific collaboration network where nodes denote authors and edges denote that the connected authors have corporations [28].In addition，in order to obtain more detailed experimental results，we divideDBLPinto11subnetworks according to the community size.The characteristics ofDBLPafter processing are displayed in Table 5.

Table 4:The characteristics of real-world networks

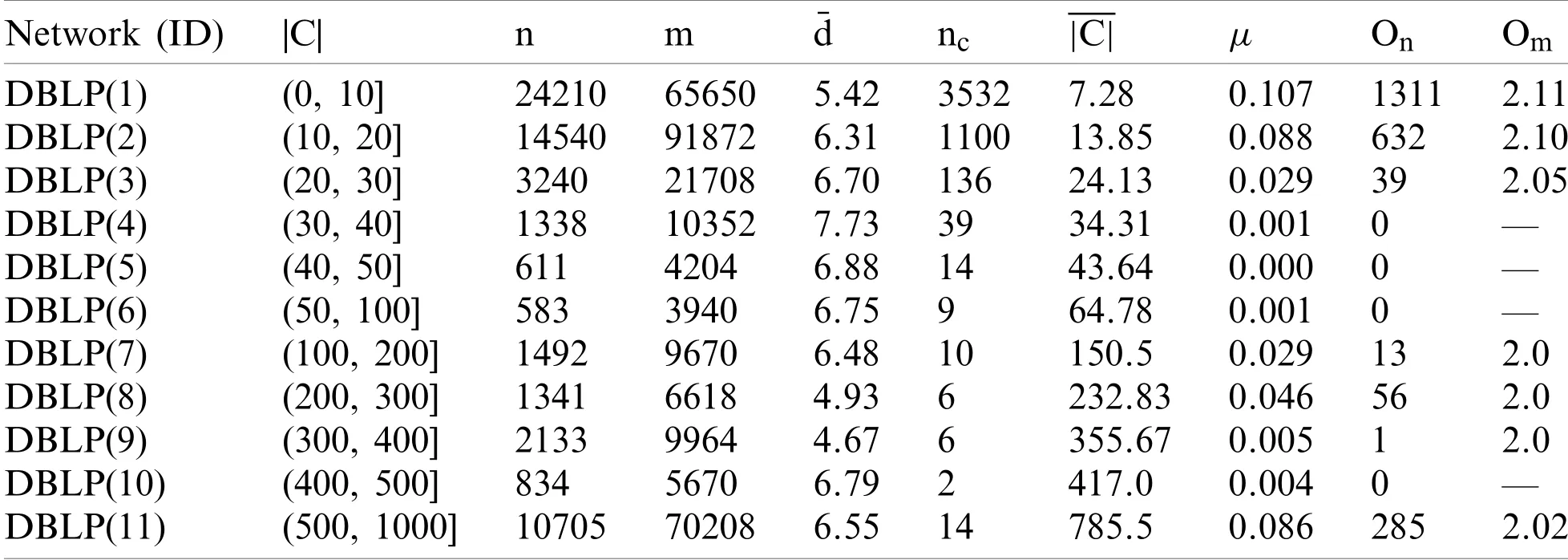
Table 5:The characteristics of DBLP sub-networks

4.5 Experimental Settings

We comparedSOLCDto6state-of-the-art local community detection algorithms:RTLCD(a robust two-stage local community detection algorithm)[16]，Clauset et al.[36]，LWP(Luo，Wang and Promislow)[37]，Chen et al.[38]，LS(link similarity)[39] andLCD(local community detection based on maximum cliques)[40].

TheRTLCDalgorithm is a robust two-stage local community detection algorithm that detects the core member of the target community to replace the seed node in the seed selection stage and expands the community based on the relation strength in the community expansion stage [16].TheClausetalgorithm extends themodularity[36] to the local community，and expands the community by adding nodes that optimize the local communitymodularity ΔR[36].TheLWPalgorithm improves the local communitymodularityto theindegreedivided by theoutdegreeand adds the termination condition of the algorithm [37].TheChenalgorithm proposes a metricL=Lin/Lexwhich is the internal relation divided by the external relation [38].

Based on the definition ofNMIandF-score，the detected local community has a high value ofNMIandF-scoreis similar to the real community in a global sense.However，the goal of seedoriented local community detection is to detect a local community with the seed node as the core member.In fact，some real-world networks have shown the power law distribution of the node degree and the core member occupies only a small scale of the networks.Therefore，in the local communities with a highNMIandF-scoremeans the seed node cannot become the core member in most cases which indicates that the seed-deviation problem occurs.

Based on the definitions ofPrecisionandRecall，in a detected community with highPrecisionand lowRecallmeans most of the members of this detected community are also the members of the real-world community in a global sense.It is common sense that most of the members of a local community should be a subset of a global community.Therefore，highPrecisionand lowRecallmeans that an algorithm prefers to detect communities in a local sense rather than detect communities in a global sense.

When the communities detected by the algorithm have highPrecisionand lowRecall，which means that the algorithm is more inclined to detect communities in the local sense rather than in the global sense.When the detected communities have high precision and low recall，which means that the algorithm is more inclined to detect communities in the local sense rather than in the global sense.Based on the definition ofLCE，the community results detected by an algorithm have highLCE，which means that the unique local communities detected by the algorithm occupy a higher proportion.Note that，we define a “seed-oriented”local community as a local community in which the seed node must satisfyLCEseed=1 and have highLCE.

The experiments are conducted on6real-world networks and 3 groups ofLFRartificial networks.Note that an algorithm running more than 24 h on a single dataset will be terminated.

4.6 Experimental Results on Real-World Networks

Table 6 lists theNMI，Recall，Precision，F-score，LCE，LCUandTimemetrics of the proposed algorithms and the other comparison algorithms on five real-world networks.

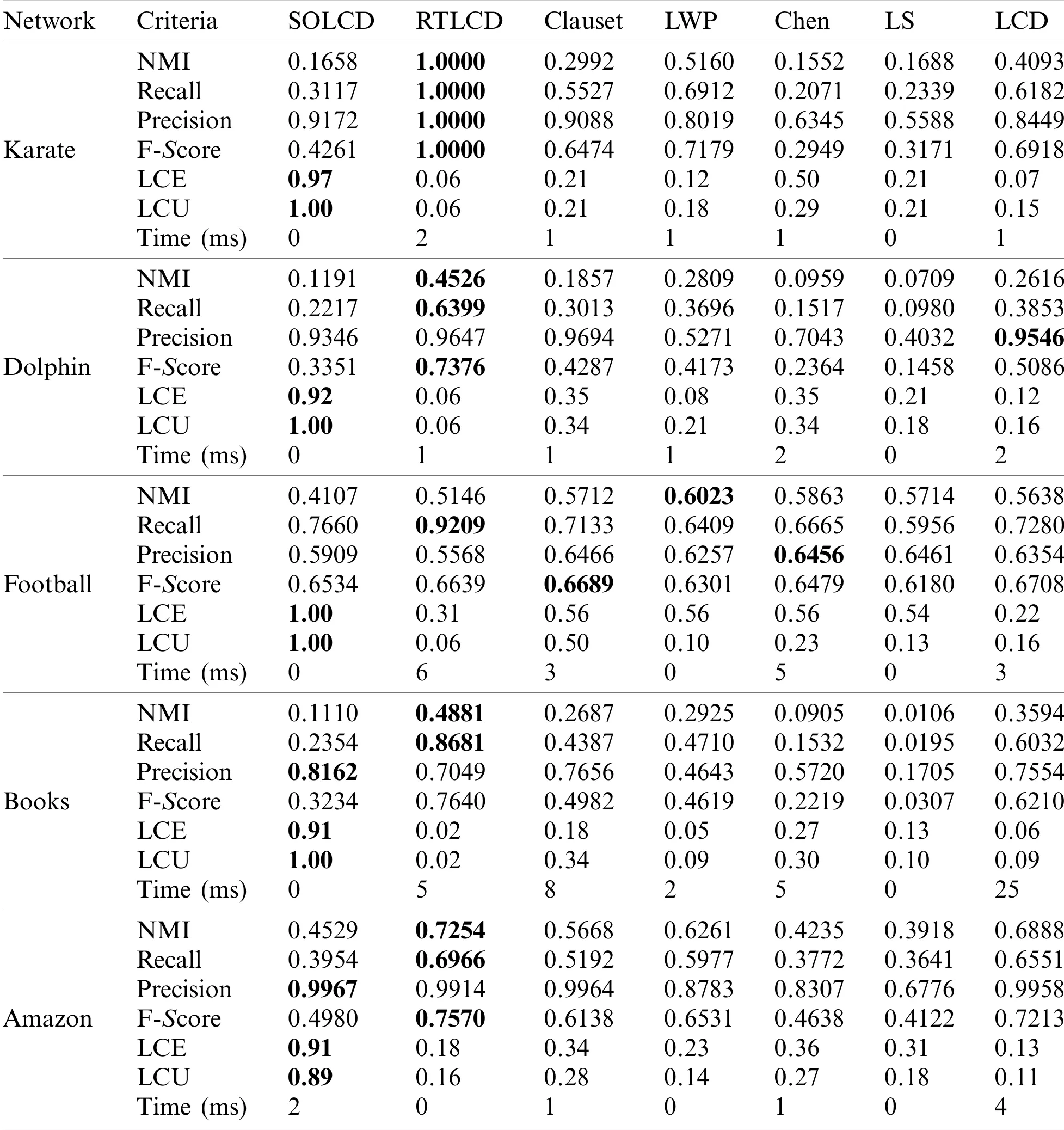
Table 6:The characteristics of the DBLP sub-networks

As shown in Table 6，we can observe thatSOLCDachieves the highestLCEandLCUon all the real-world networks，and the precision is also excellent among all algorithms，especially onbooksandAmazon.AlthoughNMI，RecallandF-scoreof these three indicators achieved bySOLCDare not good enough，we know from the analysis in Section 4.5 that high-quality seedoriented local communities are mainly measured byLCE，LCUandprecisionof three indicators rather thanNMI，RecallandF-score.Therefore，SOLCDcan achieve high-quality seed-oriented local communities among real-world networks.RTLCDis excellent inNMIandF-Scoreon all the real-world networks，which illustrates thatRTLCDis an outstanding community quality-oriented local community detection algorithm.However，RTLCDobtains the worst onLCEandLCU，which proves thatRTLCDis severely affected by the seed deviation problem.For the remaining comparison algorithms，Clauset，Chen，LWP，LSandLCD，the performance on various indicators is mediocre.That is，these algorithms have a certain ability to detect the seed-oriented local community and community quality-oriented community，but they are not skilled at this.

As shown in Figs.8a，8d and 8f，the performance of all the algorithms worsens as theIDofDBLPincreases.As Table 6 shows，the average size of the community increases as the dataset ID increases，which is the main factor that can affect the results of algorithms.The reason for this is that the increase of community size makes the edge of community become more loose，which makes algorithms more difficult to detect the community structure.

Figs.8b，8c and 8e show thatSOLCDis stable and achieves the highestLCE，LCUandPrecision，which proves thatSOLCDhas the ability to detect high-quality seed-oriented local communities.RTLCDis excellent inNMIandF-score，which illustrates thatRTLCDis skilled at detecting local communities in the global sense.However，RTLCDobtains the lowestLCE，which indicates that it has a serious seed-deviation problem.ChenandLShave goodLCEperformance，but they also have a seed-deviation problem to a certain extent.

The experimental results on real-world networks show thatSOLCDhas a great ability to achieve high-quality seed-oriented local communities among real-world networks，which proves thatSOLCDsolves the seed-deviation problem.RTLCDcan achieve the communities with the best community quality，but it is poor at detecting seed-oriented local communities.The rest of the comparison algorithms are more or less affected by the seed deviation problem.

4.7 Experimental Results on Artificial Networks

4.7.1 Experimental Results on LFR-μ

LFR-μaims to verify the ability of algorithms to reveal the community structure in response to changes in the difficulty of revealing the community structure.Fig.9 shows the performance of all the algorithms on theLFR-μartificial networks.We observe that all the algorithms show a downward trend on the metrics ofNMI，Recall，PrecisionandF-score.This phenomenon occurs because the community structure becomes increasingly more difficult to find as the mixed parameterμincreases.

Figs.9a and 9f show thatLCDandRTLCDperform excellently inNMIandF-score，which shows that these algorithms are good at detecting local communities in the global sense.However，as shown in Figs.9d and 9e，LCDandRTLCDhave highRecallsand lowPrecisions，which illustrate that these two algorithms have serious seed deviation problem.Fig.9b in whichLCDperforms the worst inLCE，confirms this matter.In contrary，SOLCDandChenhave lowRecallsand highPrecisions，which indicate that although these two algorithms find only a small number of neighbors of the seed node，these neighbors are the correct members of the seed-oriented community.Fig.9b affirms this statement.LCEofChenis obviously higher than those of other algorithms andSOLCDachieves the optimalLCEvalue.As shown in Fig.9c，SOLCDachieves the highestLCU.

Figure 8:(a-h)The performance of algorithms on DBLP

The experimental results show thatSOLCDcan achieve high-quality seed-oriented local communities as the mixed parameterμchanges，which solves the seed deviation problem.

4.7.2 Experimental Results on LFR-αsize

LFR-αsizeaims to verify the ability of algorithms to reveal the community structure when the community size changes.Fig.10 shows the performance of all the algorithms on theLFR-αsizeartificial networks.The scale values of thex-axisat the top and bottom of the graph represent the maximum and minimum of community sizes，respectively.As shown in Fig.10，the results of most of the algorithms on theNMI，Recall，PrecisionandF-scoreworsen as the maximum and minimum community size increase.The reason is as follows.As the maximum and minimum community size increase，the community structure becomes more diverse，and the boundary of the community becomes fuzzy，which makes it difficult for the algorithms to identify the community structure.Fig.10c shows thatSOLCDis stable at the highestLCU.

Figure 9:(a-h)The performance of algorithms on LFR-μ

As shown in the Figs.10b and 10f，SOLCDis stable at a high level onLCE，LCUandPrecisionregardless of whether the parameterαsizechanges，which proves that SOLCD can effectively detect seed-oriented local communities.RTLCDandLCDare stable on the indices ofNMIandF-score，which illustrates that these two algorithms are robust to the parameterαsizein detecting local communities in the global sense.However，RTLCDandLCDperform extremely poorly onLCEandLCU，which indicates that these methods have serious seed deviation problems.ChenandClausethave good performance on the index of Precision，and moderate performance onLCEandLCU，which shows that these two algorithms have certain capabilities to detect seed-oriented local communities，but they still have seed deviation problems to a certain extent.

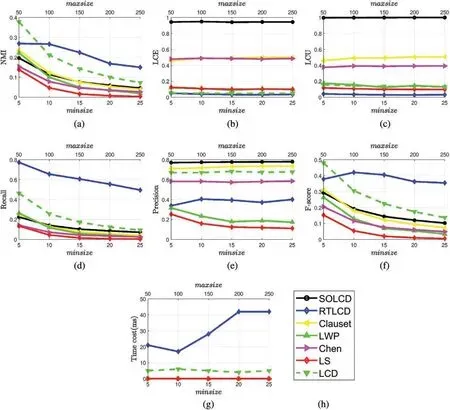
Figure 10:(a-h)The performance of algorithms on LFR-αsize

The experiments prove thatSOLCDis robust to changes in the community size.As the the maximum and minimum community size increase，SOLCDcan still achieve high-quality seed-oriented local communities which indicates thatSOLCDsolves the seed deviation problem.

4.7.3 Experimental Results on LFR-αdegree

LFR-αdegreeaims to test the performance of algorithms on revealing the community structure as the node degree changes.Fig.11 displays the results of all the algorithms on theLFR-αdegreeartificial networks.The scale values of the x-axis at the top and bottom of the graph represent the maximum and mean degree of nodes in the network respectively.Figs.11a and 11f show that the performance of most algorithms onNMIandPrecisionimprove slightly as the parameterαdegreeincreases.The reason for this outcome is as follows.Increasing the parameterαdegreemakes the relationship between nodes become more diverse，so it can provide more node information which makes the algorithms easier to detect the community structure;however，it also increases the complexity of the network，which prevents algorithms from exploring the community structure.Therefore，the curves fluctuate.

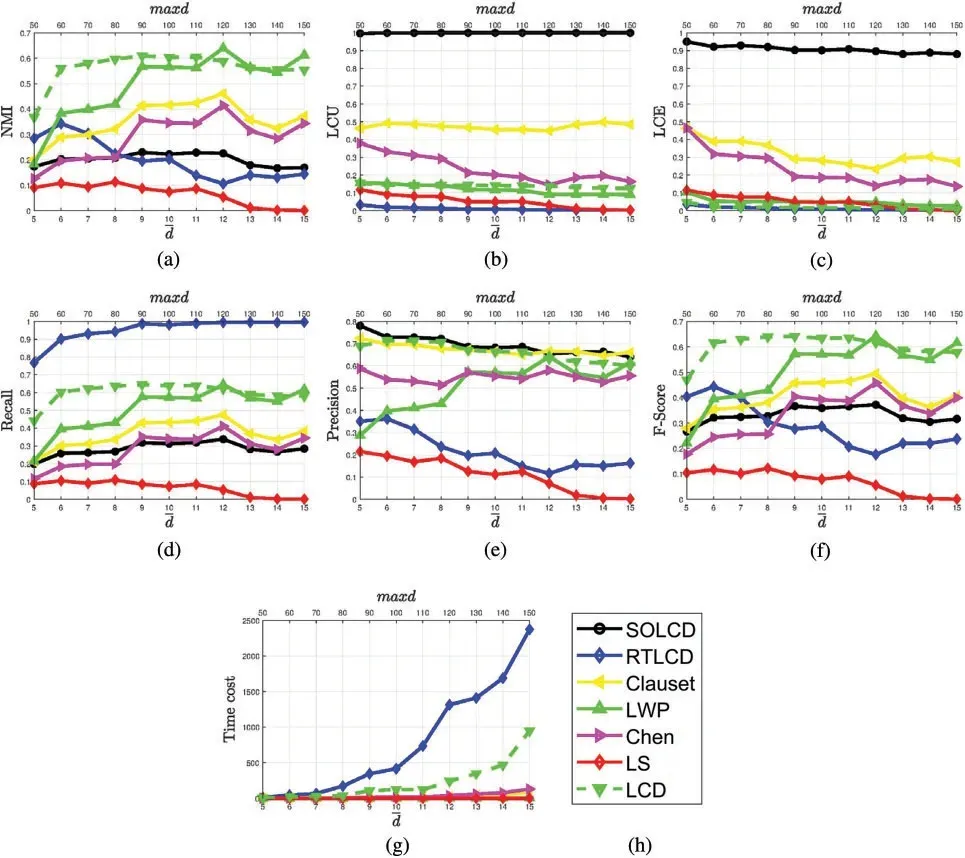
Figure 11:(a-h)The performance of algorithms on LFR-αdegree

Fig.11 shows thatLCEofSOLCDdecreases slightly as the parameterαdegreeincreases，but it remains at a high level.TheLCUandPrecisionofSOLCDare outstanding.LCDandLWPperform excellently on the indices ofNMIandF-score，which indicates that these two algorithms have great abilities to detect the local communities in the global sense.Unfortunately，LCDandLWPobtain poorLCEswhich proves that they experience the seed deviation problem.ClausetandChenhave good performance onPrecision，and lowLCUsandLCEs，which proves that these two algorithms have certain seed-oriented local community detection abilities but they are not considerable.RTLCDunderperforms in all indicators exceptRecall，which illustrates thatRTLCDcan neither effectively detect local community in global sense nor detect seed-oriented communities in a local sense when the network has a high degree.

The results indicate that SOLCD has some seed-deviation problems as the mean and maximum node degree increase，but it can achieve a high-quality seed-oriented local community.

4.7.4 Experimental Results for the Seed Dependence Problem

To perform a detailed analysis of theseed dependenceproblem，this paper lists the valid communities generated by seed nodes with different node influences.We take the degree centrality as the node influence measure.We divide all the nodes into ten parts according to their node influence in descending order.Taking Fig.12 as an example，Fig.12a is the distribution of the valid seed-oriented local communities detected by the algorithms on theDBLP1network，and so on.The abscissa represents the ranking of the seed’s node influence among the node influences of all nodes in the network(e.g.，‘0.1’represents that the seed’s node influence is in the top 10%of all nodes，and ‘1’represents that the bottom 10% of seed nodes).The ordinate represents the proportion of valid seed-oriented local communities in all communities detected by the algorithms.Table 7 displays the standard deviation(SD)，arithmetic mean and coefficient of variation(CV)of the proportion of valid seed-oriented local communities detected by all the comparison algorithms on a group ofDBLPnetworks.Thestandard deviationis a measure of the dispersion of the data distribution，which is used to measure the deviation of data from the arithmetic mean.The smaller the standard deviation is，the less these values deviate from the mean，and vice versa.When comparing the dispersion of the two groups of data，the measurement scales of the two groups of data are too different to be compared directly using the standard deviation.At this time，thecoefficient of variationis required，which is the ratio of the standard deviation and arithmetic mean.

Fig.12 shows that the curve ofSOLCDis stable at the top of Figs.12a-12f but fluctuates in Figs.12g-12k.The above figures show that the nodes in the middle ranking have more difficulty obtaining local communities with them as the core than the nodes at the top of the ranking and the nodes at the bottom of the ranking.There are three reasons for this phenomenon.First，the nodes at the bottom of the ranking have a small influence scope，so it is easy to obtain local communities with these nodes as the core.Second，although the nodes at the top of the ranking have a large influence scope，they can easily attract adjacent nodes to their community because of their strong node influence，so it is easy to obtain local communities with these nodes as the core.Third，for the nodes at the middle of the ranking，there may be multiple adjacent nodes with the same node influence.Therefore，these nodes with the same node influence will be bypassed in the community expansion process，which leads to the irregularity of the resulting community，and it fails to form a local community with these nodes at the middle of the ranking as the core.From the Table 7 shows thatSOLCDhas the highest mean on allDBLPnetworks and the lowestCVexcept onDBLP(1)，which illustrates that compared with the other algorithms，SOLCDis more stable in terms of the seed dependence problem.However，theSDofSOLCDon some networks is high，which indicates thatSOLCDstill has a certain seed dependence problem.The other six comparison algorithms show sharp fluctuations in all subfigures of Fig.12 and have smallSDonly on individual network in Table 7 which proves that all these algorithms have serious seed dependence problems.

Table 7:The standard deviation(SD)，arithmetic mean and coefficient of variation(CV)of the proportion of the valid seed-oriented local communities detected by all the comparison algorithms on a group of DBLP networks

Figure 12:(a-l)The distribution of the valid seed-oriented local communities detected by the algorithms on a group of DBLP networks

Fig.13 shows that the curves of each algorithm in different figures are basically consistent.That is，the experimental results are not affected by parameterμ.The performance ofSOLCDimproves as the node ranking decreases，and the overall performance is excellent.Clausethas perfect performance on the top node ranking，but its performance drops rapidly as the node ranking decreases.The performance ofLCDalso drops rapidly as the node ranking decreases，but the overall performance is not as good as that ofClauset.The curves ofRTLCD，LWPandLSare always at the bottom.The performance ofChenis very stable and does not fluctuate with the node ranking.Table 8 shows thatSOLCDachieves the highest mean and a slightly higherSDandCVthan Chen and LS.Chenachieves the lowestSDandCV，but its mean is much lower than that ofSOLCD.LSperforms excellently on SD;however，itsCVis high，and the mean is low.The other algorithms have poor performance on the mean，SDorCV.The experimental results show thatSOLCDbasically has no seed dependence problem onLFR-μartificial networks.Chen has no seed dependence problem，but its seed-oriented community detection ability is much weaker than that ofSOLCD.LShas no seed dependence problem，but has no ability to detect the seed-oriented community.The other algorithms are seriously affected by seed dependence problems.

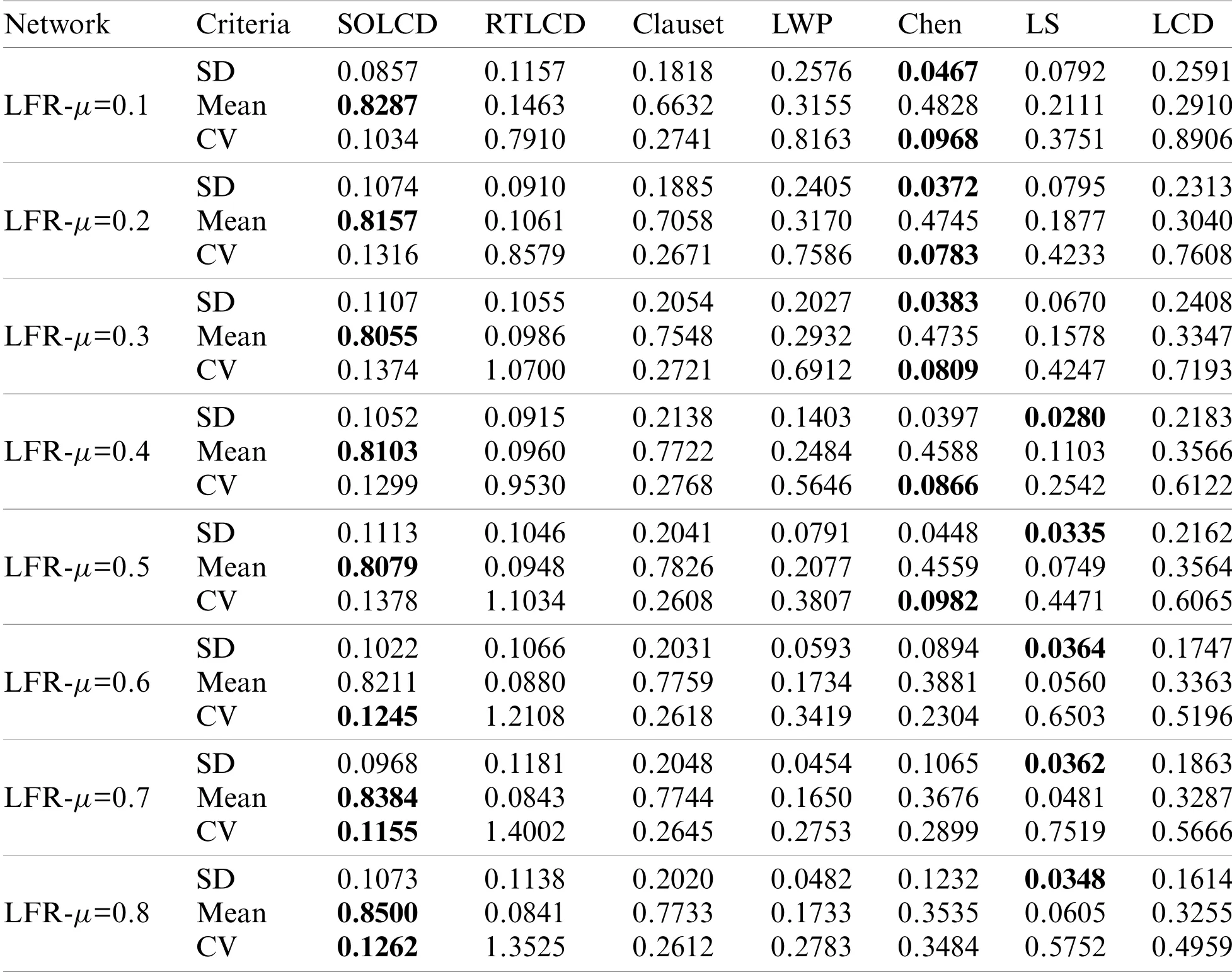
Table 8:The standard deviation(SD)，arithmetic mean and coefficient of variation(CV)of the proportion of the valid seed-oriented local communities detected by all the comparison algorithms on a group of LFR-μ artificial networks

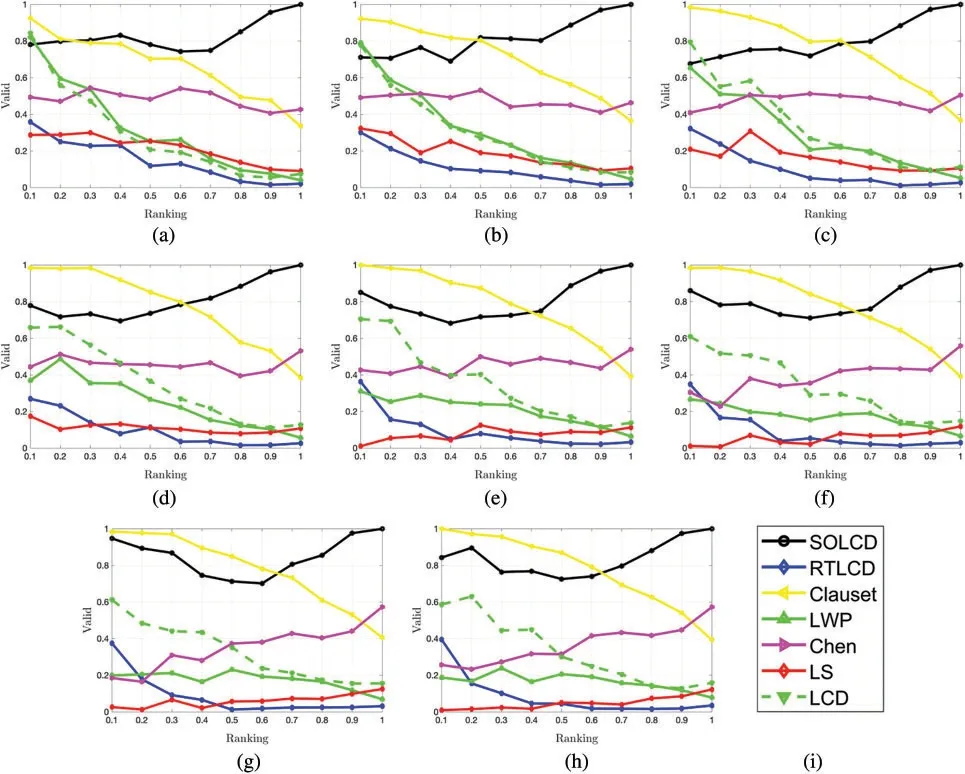
Figure 13:(a-i)The distribution of the valid seed-oriented local communities detected by the algorithms on a group of LFR-μ artificial networks

Fig.14 and Table 9 show that the curves and data are roughly the same as those in Fig.13 and Table 8.Therefore，we can conclude that the performance of algorithms is similar onLFRαsizeartificial networks andLFR-μartificial networks.

Fig.15 shows thatSOLCDstill performs stably，as in the above two groups of experiments.That is，the performance ofSOLCDdoes not change as the parameterαdegreeincreases.However，the curves of the other algorithms decrease sharply as the parameterαdegreeincreases.The reason for this phenomenon is as follows.Table 10 shows thatSOLCDachieves the highest mean and lowestCVon most networks and a slightly higherSDthanRTLCD，Chen and LS.However，the mean ofRTLCDand LS is so low that the results have no reference value.Chen performs well with a low parameterαdegreebut worsens the parameterαdegreeincreases.The experimental results show thatSOLCDbasically has no seed dependence problem onLFR-αdegreeartificial networks.The other algorithms are seriously affected by seed dependence problems and are seriously affected by parameterαdegree.

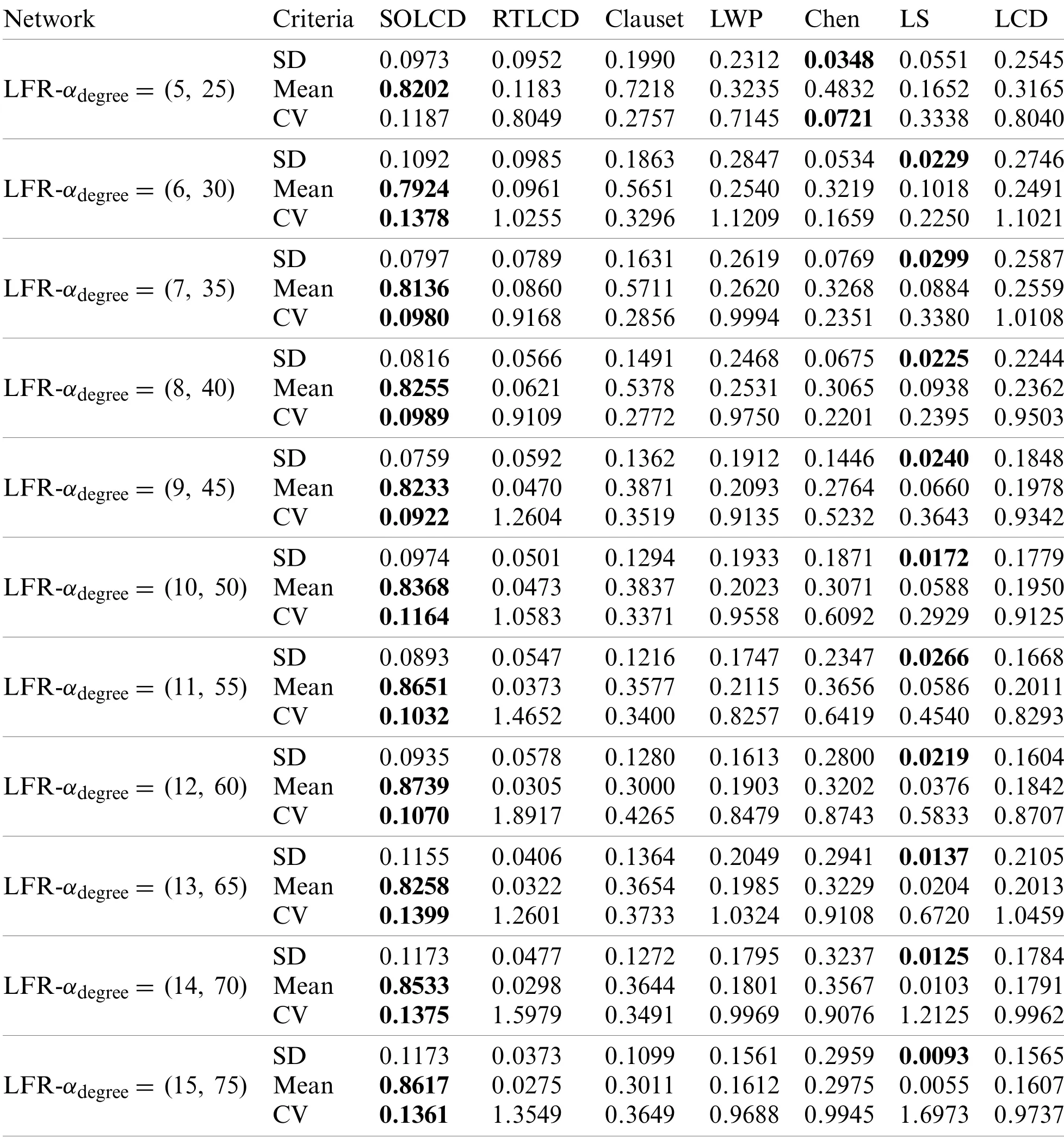
Table 10:The standard deviation(SD)，arithmetic mean and coefficient of variation(CV)of the proportion of the valid seed-oriented local communities detected by all the comparison algorithms on a group of LFR-αdegree artificial networks

Figure 14:(a-f)The distribution of the valid seed-oriented local communities detected by the algorithms on a group of LFR-αsize artificial networks

Table 9:The standard deviation(SD)，arithmetic mean and coefficient of variation(CV)of the proportion of the valid seed-oriented local communities detected by all the comparison algorithms on a group of LFR-αsize artificial networks

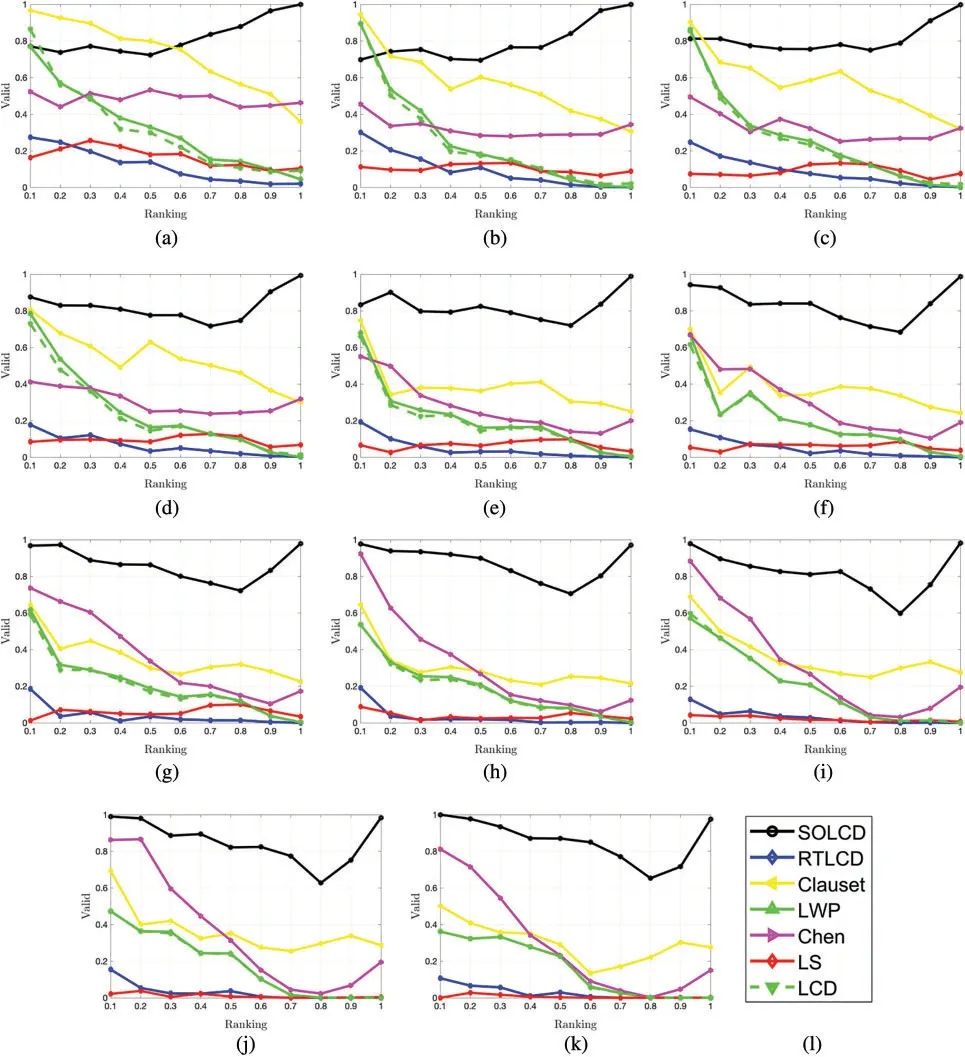
Figure 15:(a-l)The distribution of the valid seed-oriented local communities detected by the algorithms on a group of LFR-αdegree artificial networks

4.8 The Discussion of the Experimental Results

Based on the above experimental results，we can obtain the following conclusions.First，the proposed algorithm has a great ability to detect high-quality seed-oriented local communities among real-world networks，which proves thatSOLCDsolves the seed-deviation problem.Second，the seed-oriented local community detection ability of the proposed algorithm is not affected by parametersμ，αsizeandαdegree.Third，SDandCVare the proportions of valid seedoriented local communities detected bySOLCDon real-world networks and artificial networks，respectively.SOLCDachieves a lowSDandCV，which proves thatSOLCDcan detect highquality seed-oriented local communities with nodes with different node influences as seeds.This illustrates thatSOLCDsolves seed dependence problems.In addition，SOLCDachieves excellent results on groups of artificial networks with different parameters，which shows thatSOLCDhas strong robustness.However，there are still problems to be solved.SOLCDstill does not completely resolve the seed dependence problem，especially when taking the nodes with medium node influence as the seed.

5 Conclusion

Research on local community detection has achieved excellent achievements.However，there are still some problems to be solved，such as the seed deviation problem，the seed dependence problem and the parameter dependence problem.In order to solve these problems，this paper proposes a seed-oriented local community detection algorithm，namedSOLCD，based on influence spreading.To solve the seed deviation problem and the seed dependence problem，we propose a seed-oriented algorithm，which always takes the given node as the seed，and always takes the seed as the influence core in the community expansion process.To solve the parameter dependence problem，we propose a local community detection algorithm based on influence spreading without any parameters.In addition，we propose a local community effectiveness index(LCE)and a local community uniqueness index(LCE)to estimate the quality of seed-oriented local communities.Efficient and rapid detection of seed-oriented communities can improve the accuracy of personalized recommendation of goods and information and help public opinion analysis.

This paper comparesSOLCDwith six other state-of-the-art local community detection algorithms onLFRartificial networks and real-world networks.The experimental results show thatSOLCDhas a great ability to detect high-quality seed-oriented local communities among realworld networks，which proves thatSOLCDsolves the seed deviation problem.Taking nodes with different node influences as seeds，SOLCDcan detect high-quality seed-oriented local communities，which illustrates thatSOLCDsolves the seed dependence problem.In addition，SOLCDachieves excellent results on groups of artificial networks with different parameters，which shows thatSOLCDhas strong robustness.

However，there are still problems to be solved.SOLCDstill has not completely resolved the seed dependence problem，especially when taking the nodes with medium node influence as the seed.We will focus on solving the seed dependence problem completely in future research.

Funding Statement:National Natural Science Foundation of China(Nos.61672179，61370083，61402126)，Heilongjiang Province Natural Science Foundation of China(No.F2015030)，Science Fund for Youths in Heilongjiang Province(No.QC2016083)and Postdoctoral Fellowship in Heilongjiang Province(No.LBH-Z14071).

Conflicts of Interest:The authors declare that they have no conflicts of interest to report regarding the present study.