Asymptotic Approximations of Apostol-Tangent Polynomials in Terms of Hyperbolic Functions

Cristina B.Corcino，Wilson D.Castãneda Jr. and Roberto B.Corcino，★

1Research Institute for Computational Mathematics and Physics，Cebu Normal University，Cebu City，6000，Philippines

2Mathematics Department，Cebu Normal University，Cebu City，6000，Philippines

3Department of Mathematics，Cebu Technological University，Cebu City，6000，Philippines

ABSTRACT The tangent polynomials Tn(z) are generalization of tangent numbers or the Euler zigzag numbers Tn.In particular，Tn(0)=Tn.These polynomials are closely related to Bernoulli，Euler and Genocchi polynomials.One of the extensions and analogues of special polynomials that attract the attention of several mathematicians is the Apostol-type polynomials.One of these Apostol-type polynomials is the Apostol-tangent polynomials Tn(z，λ).When λ=1，Tn(z，1)=Tn(z).The use of hyperbolic functions to derive asymptotic approximations of polynomials together with saddle point method was applied to the Bernoulli and Euler polynomials by Lopez and Temme.The same method was applied to the Genocchi polynomials by Corcino et al.The essential steps in applying the method are(1)to obtain the integral representation of the polynomials under study using their exponential generating functions and the Cauchy integral formula，and(2)to apply the saddle point method.It is found out that the method is applicable to Apostol-tangent polynomials.As a result，asymptotic approximation of Apostol-tangent polynomials in terms of hyperbolic functions are derived for large values of the parameter n and uniform approximation with enlarged region of validity are also obtained.Moreover，higher-order Apostol-tangent polynomials are introduced.Using the same method，asymptotic approximation of higherorder Apostol-tangent polynomials in terms of hyperbolic functions are derived and uniform approximation with enlarged region of validity are also obtained.It is important to note that the consideration of Apostol-type polynomials and higher order Apostol-type polynomials were not done by Lopez and Temme.This part is first done in this paper.The accuracy of the approximations are illustrated by plotting the graphs of the exact values of the Apostol-tangent and higher-order Apostol-tangent polynomials and their corresponding approximate values for specific values of the parameters n，λ and m.

KEYWORDS Apostol-tangent polynomials;tangent polynomials;Genocchi polynomials;Hermite polynomials;asymptotic approximation

1 Introduction

The Apostol-tangent polynomials denoted byTn(z;λ)，λ/=0 are defined by generating function(see [1])

2 Asymptotic Expansions of Apostol-Tangent Polynomials

The accuracy of the asymptotic formula obtained in Eq.(5)is shown in Fig.1.

To enlarge the region of validity of Eq.(5)and obtain an asymptotic expansion valid in a larger region，the following theorem will be utilized.

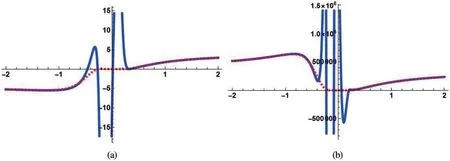
Figure 1:Solid lines represent Tn(nx+1;λ) for several values of n，whereas dashed lines represent the right-hand side of(5)with z=x，both normalized by the factorwhere we choose α=0.2(a) n=7 and λ=4(b) n=14 and λ=9

The accuracy of the asymptotic formula obtained in Eq.(18)is shown in Fig.2.The accuracy of the approximation in the oscillatory region is better that that the of the formula in Eq.(5).

Figure 2:Solid lines represent Tn(nx+1;λ) for several values of n，whereas dashed lines represent the right-hand side of Eq.(18)with z ≡x，both normalized by the factorwhere we choose α=0.2.(a) n=7 and λ=4(b) n=14 and λ=9

Remark 2.4.Takingλ= 1，Theorem 2.1 and Theorem 2.3，respectively，will give uniform approximationformula and an asypmtotic expansion with enlarged region of validity which are same formulas as those obtained in [17] for the tangent polynomials.

3 Approximation of Higher-Order Apostol-Tangent Polynomials

Higher-order Apostol-tangent polynomials are defined by the generating function

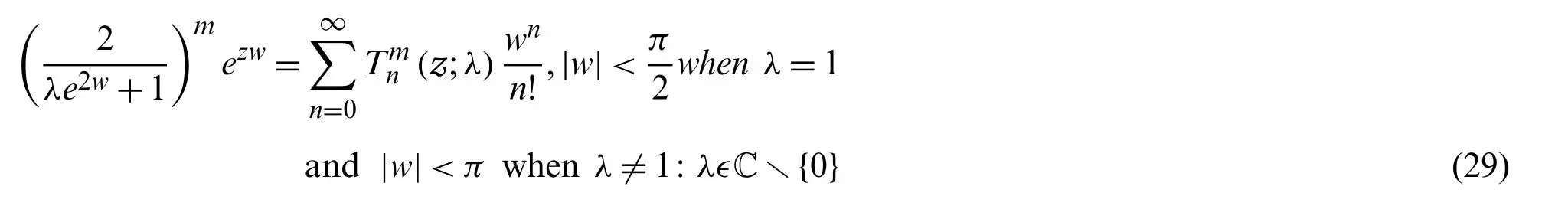
In this section，it is shown that the method in Section 2 can be extended to obtain asymptotic expansion of the Apostol-tangent polynomials of orderm.

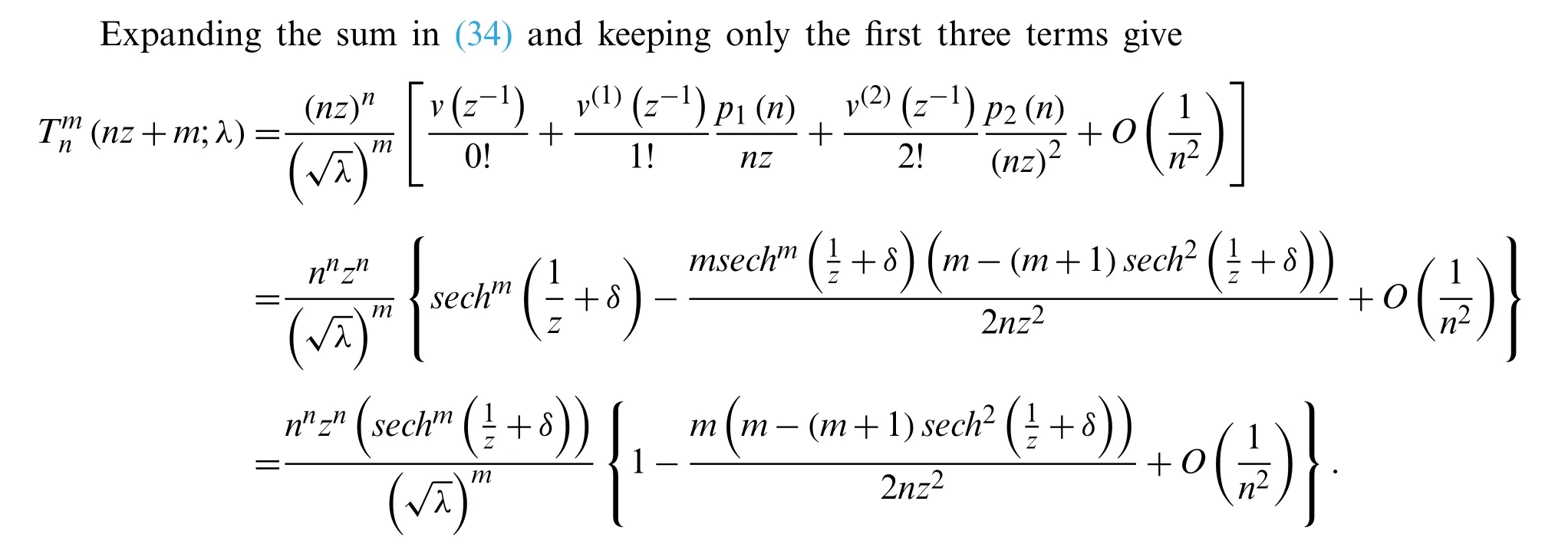
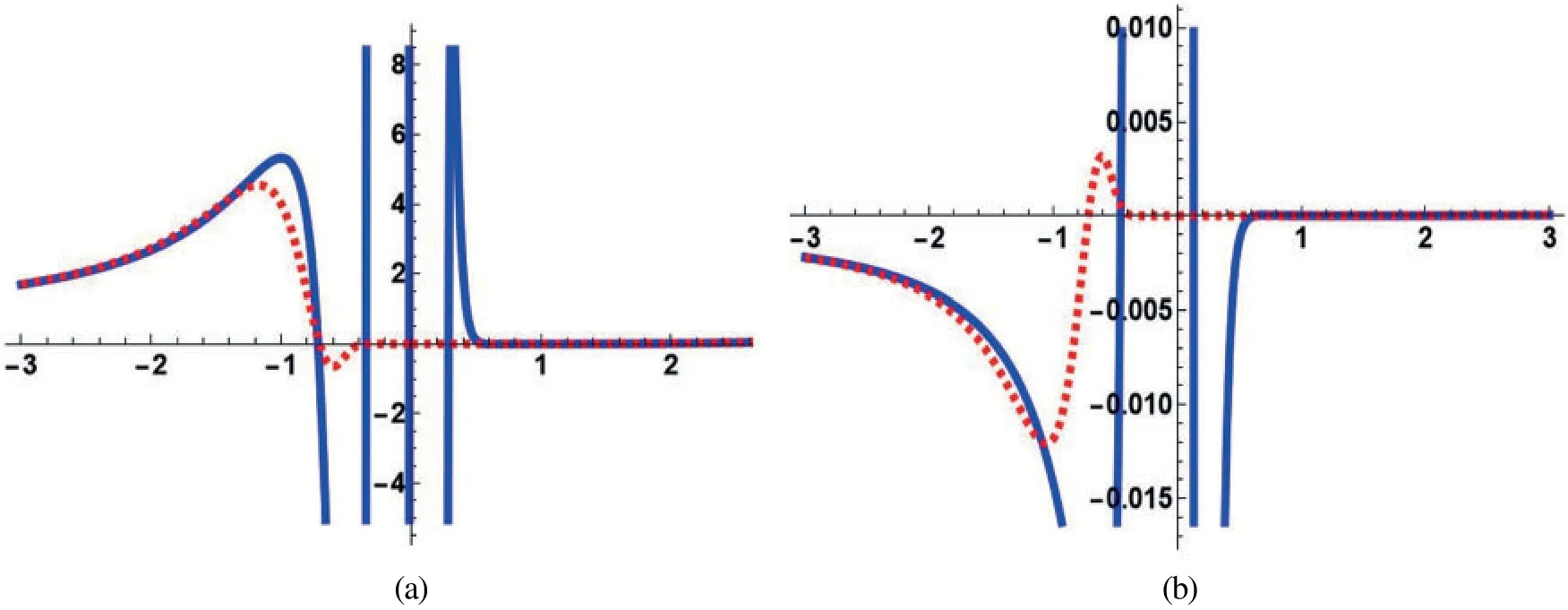
Figure 3:Solid lines representfor several values of n and m，whereas dashed lines represent the right-hand side of Eq.(30)with z ≡x，both normalized by the factorwhere we choose α=0.2(a) m=7，n=10 and λ=5(b) m=8，n=7 and λ=6

The accuracy of the asymptotic formula obtained in Eq.(30)is shown in Fig.3.

Proof.This follows from Theorem 3.1 by takingλ=1.To enlarge the region of validity of Eq.(30)and obtain an asymptotic expansion valid in a larger region the following theorem will be used.

Figure 4:Solid lines in(a)and(b)representfor n=3，m=3，whereas dashed lines in(a)and(b)represent the right hand side of Eqs.(30)and(39)，respectively，with z ≡x，both normalized by the factorwhere we choose a=0.5(a) n=3，m=3 and λ=3(b)n=3，m=3 and λ=3

The comparison of the accuracy of the asymptotic formula obtained in Eq.(30)and Eq.(39)is shown in Fig.4.

4 Conclusion

The saddle-point method and the use of hyperbolic functions are shown to give good approximations to the Apostol-tangent polynomials.Uniform approximations of the Apostoltangent polynomials and of higher-order Apostol-tangent polynomials are derived.Moreover，approximation formulas with larger region of validity are obtained.The computations to derive the approximation formulas with larger region of validity for the case of Apostol-tangent polynomials of order m are quite tedious and the formulas obtained are original.Corollaries are being stated to explicitly give the corresponding formulas for the special caseλ= 1 and can be used as check formulas of the general case.It will be interesting also to investigate if the methods used in the paper will be applicable to the Apostol-tangent-Bernoulli polynomials and Apostol-tangent-Genocchi polynomials of higher order.

For future research work，one may try to investigate more properties of Apostol-tangent and higher order Apostol-tangent polynomials and establishq-analogues of these polynomials(see [20-22]).

Funding Statement:This research is funded by Cebu Normal University through its Research Institute for Computational Mathematics and Physics(RICMP).

Conflicts of Interest:The authors declare that they have no conflicts of interest to report regarding the present study.